2 Способ.

Экспериментальное определение скорости проводят так. Рассмотрим движение тела, брошенного под углом  к горизонту (вниз). В точке В скорость тела V_эк может представляться в виде двух компонентов: V_х и V_y – скорости в вертикальном и горизонтальном направлениях.

На рис.1: V_x=V_эк cos

V_y=V_эк sin (*)

Отрезки х и у могут быть определены из законов поступательного движения. В нашем случае: х=V_xt

(17.4)

где x=CD – горизонтальное перемещение тела;

y=BC - по вертикали;

Отсюда (из (*) и (17.4)) искомая скорость:

(17.5)

Из формулы (17.4) найдем время 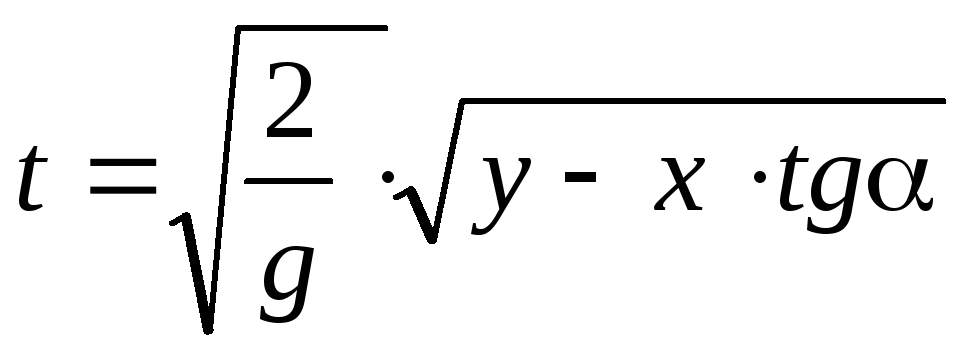(17.6) и подставим в (17.5). После подстановки получим окончательное выражение для определения скоростиV_эксп.

(17.7)

Измерение и обработка результатов измерения

1. Измеряют длину наклонной плоскости l, расстояние по горизонтали b, высоту подъема и вычисляют cos и tg для трех случаев высоты.

2. Пускают тело из произвольной точки А по наклонной плоскости. Измеряют расстояние х=CD (от точки С до отметки на бумаге) и у=ВС постоянно для различных высот. Опыт повторяют для различных тел с различных высот, не менее 9 опытов.

3. По формуле (17.7) подсчитывают скорости тел в точке В. Полученные значения сравнивают со значениями для тех же образцов по формуле (17.2). Сделайте вывод.

4. По формуле (17.6) находят время для различных образцов.

5. Взвешивают испытуемое тело (шар, цилиндр, полый цилиндр), измеряют радиусы образцов и определяют моменты инерции тел.

Все вычисления заносят в таблицу:

Таблица 17.1

№ опыта образец	h	x	Vтеор	I	k	Vэксп	t
1 2 3

Контрольные вопросы

1. Превращения энергия при скатывании тела с наклонной плоскость.

2. Вывод формулы скорости тела из закона сохранения энергии.

3. Вывод формулы скорости тела из определения его координат.

4. Момент инерции тел вращения.

Лабораторная работа № 18 изучение затузающих колебаний

На практике всякое колебание материальной точки, которое не поддерживается извне, затухает, т.е. амплитуда его колебаний с течением времени уменьшается.

Причинна затухания обуславливается силами, тормозящими движение, например, силой трения в месте подвеса при колебании маятника, или силой сопротивления среды.

Сила сопротивления среды зависит от скорости движения материальной точки, и в случае малых скоростей ее можно считать пропорциональной скорости и направленной в сторону, противоположную вектору скорости, т.е. сила сопротивления,

, (18.1)

где r- постоянная величина, называемая коэффициентом сопротивления.

Тогда полная сила, действующая на точку, совершающую колебательное движение с учетом силы сопротивления, будет равна:

(18.2)

Запишем второй закон Ньютона для такого колебательного движения

(18.3)

или

(18.4)

Обозначим

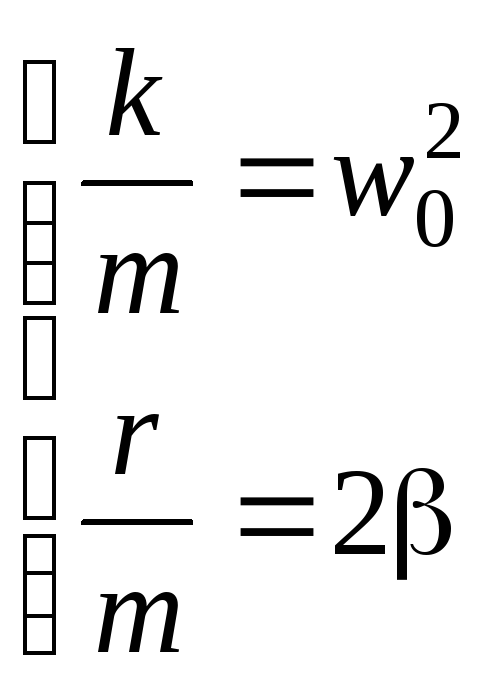(ранее известно) (18.5)

Тогда уравнение (4) примет вид

(18.5а)

Уравнение (18.5а) является дифференциальным уравнением затухающего колебания под действием F_упр и F_сопр.

Решением этого дифференциального уравнения является выражение вида:

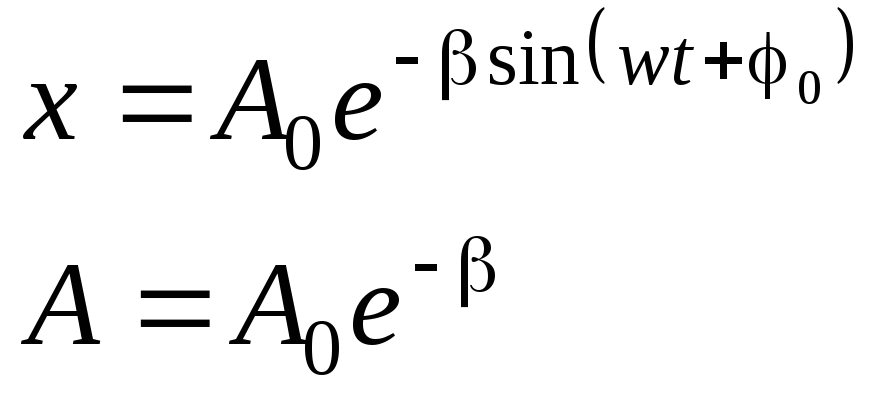(18.6)

А- амплитуда затухающих колебаний.

Колебание происходит по синусоидальному закону.

Затухающие колебания представляют собой периодические колебания, т.к. в них никогда не повторяются величины амплитуды, скорость и ускорение. Величина в выражении (6) называется частотой затухающих колебании и равна:

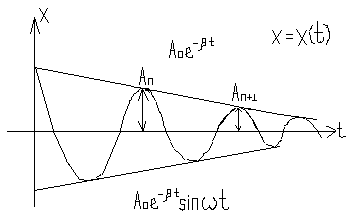(18.7)

где w₀ – частота незатухающих колебаний системы в отсутствие сил трения, т.е. собственная частота колебаний системы, а называется коэффициентом затухания. Если сопротивление среды мало, тоw₀²>² и величина положительна, тогда период затухающих колебаний равен:

(18.8)

Период колебаний точки под действием упругой силы в среде с сопротивлением больше, чем период колебаний точки такой же массы в среде без сопротивления.

Характеристиками затухающего колебания являются логарифмический декремент затухания и коэффициент затухания.

Поскольку амплитуда затухающих колебаний уменьшается со временем, то для характеристики уменьшения ее вводят величину, называемую декрементом затухания. Найдем отношение значений амплитуды затуханий колебаний в моменты времени t и (t+T), где T-период этих колебаний (рис.18.1).

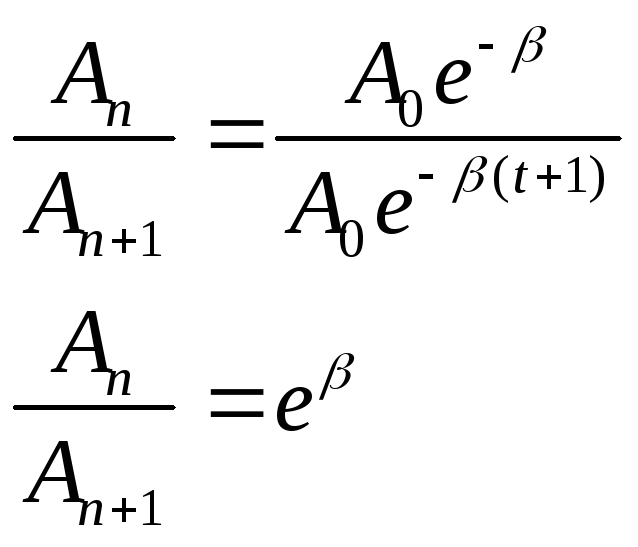(18.9)

Такое отношение называют декрементом затухания. Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени Т, называется логарифмическим декрементом затухания 

(18.10)

Из уравнения (18.10) видно, что логарифмический декремент затухания связан с коэффициентом затухания . Выясним физический смысл  и .

Обозначим через  промежуток времени, за который амплитуда уменьшает в е раз.

Тогда , (18.11)

откуда (18.12)

Время называется временем релаксации. Пусть, например, n=10. Это означает, что амплитуда колебаний убывает в е раз 10 с. Пусть n- число колебаний, после которых амплитуда уменьшается в е раз, т.е.

, (18.13)

тогда (18.14)

Следовательно, логарифмический декремент затухания есть физическая величина, обратная числу n, по истечении которых амплитуда убывает в е раз. Например, =10^-2 – это значит, что амплитуда убывает в е раз по истечении 100 колебаний. Если затухание колебаний не очень велико, то оно почти совсем не сказывается на величине периода колебаний.

При большем коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний.

При некотором коэффициенте сопротивления r=2mw₀ (когда =w₀), называемом критическим, частота колебаний обращается в нуль.

Следовательно, колебания прекращаются: система выведения из положения равновесия какими-либо внешними силами после прекращения действия этих сил монотонно возвращается в положение равновесия, не совершая колебательного движения. Такой процесс называется апериодическим движением (рис.18.2). Колебательное движение отличается от апериодического тем, что при колебательном движении система, возвращаясь в положение равновесия, имеет некоторый запас кинетической энергии. А в случае апериодического движения вся механическая энергия колеблющейся системы ее возвращения в положение равновесия оказывается израсходованной на преодоление трения.

Упражнение 1.

Определение логарифмического декремента и коэффициента затухания пружинного маятника методом сравнения амплитуд и изучение зависимости логарифмического декремента.

А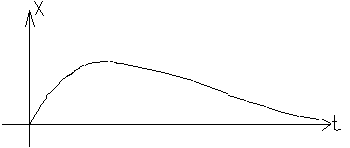мплитуды колебаний, отстоящие друг от друга на один период, мало отличаются друг от друга, и поэтому для более точного определения амплитуды коэффициента затухания обычно измеряют амплитуды, отстоящие друг от друга по времени наn периодов, т.е. t=nТ (18.16)

;

Равенство отношений ; (18.17)

…

позволяет записать следующее: (18.18)

Отсюда (18.19)

(18.20)

Используя (18.16), напишем для :

(18.21)