Определение средней силы взаимодействия при ударе шаров равной массы

Постановка задачи. Определить среднюю силу взаимодействия шаров равной массы m₁=m₂=m при ударе. Угол начального отклонения правого шара равен . Длина подвесов l₁=l₂=l, время соударения .

Указания к решению. Импульсы сил, действующих на шары, равны

(8.6)

Из (8.6) при m₁=m₂=m, ₁=_2,0=0, ₂=_1,0= получим

(8.7)

Здесь F₁₂ и F₂₂ среднее за время удара значение сил взаимодействия между шарами.

Применим закон сохранения механической энергии при движении правого шара до удара (рис.8.1):

(8.8)

Из (8.7) и (8.8) находим

(8.9)

Отметим, что реальный удар не является абсолютно упругим, поэтому часть механической энергии системыW перейдет в другие виды энергии (например, в теплоту). Доля механической энергии, перешедшей в другие виды энергии, может быть оценена по формуле

(8.10)

Здесь ^’ – угол отклонения левого шара после удара.

Определение массы одного из шаров при их неупругом соударении

Постановка задачи. Два шара массами m₁ и m₂ подвешены на нитях так, что их центры находятся на одном уровне. Правый шар с известной массой m₁ (рис.8.2) отклоняют на угол ₁ и затем отпускают. При ударе шары соединяются замком и движутся вместе (осуществляется абсолютно неупругий удар). Шары при этом отклоняются на угол ₂. Определить массу левого шара.

Указание к решению. Применим закон сохранения механической энергии для определения скорости правого шара в момент соударения:

(8.11)

Здесь l – длина подвеса. Так как проекция внешних сил на ось 0_х равна нулю, можно воспользоваться законом сохранения импульса в проекции на ось 0_х. При неупругом ударе шаров получим

(8.12)

Здесь U- скорость обоих шаров после неупругого удара.

Применим закон сохранения механической энергии при движении шаров после удара:

(8.13)

Решая систему уравнений (8.11)-(8.13), получим соотношение для определения массы левого шара

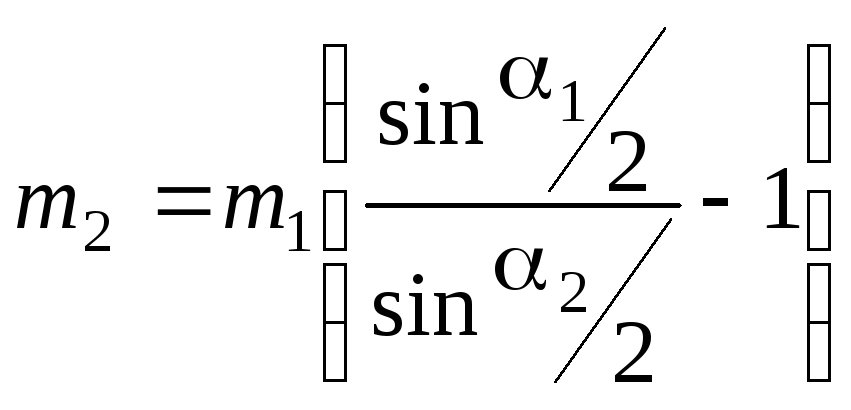(8.14)

Определение среднего момента относительно точки подвеса, создаваемого силой, возникающей при взаимодействии упругих шаров

Постановка задачи. Определить средний момент сил, возникающий при взаимодействии шаров равной массы m₁=m₂=m, равного радиуса R₁=R₂=R при упругом ударе. Угол начального отклонения правого шара равен , длины подвесов (до центров шаров) l₁=l₂=l время соударения .

Указания к решению. В момент соударения правый шар обладал моментом импульса относительно точки подвеса, равным L=I, где момент инерции I согласно теореме Гюйгенса- Штейнера равен

(2.15)

Используя (2.8), найдем

(2.16)

Из основного закона динамики вращательного движения следует

(2.17)

Подставляя во второе соотношение (2.17) соотношения (2.15) и (2.16), получим среднее значение момента силы

8.3. Схема абсолютно упругого удара 8.4. Область существенного смятия при абсолютно упругом ударе двух шаров

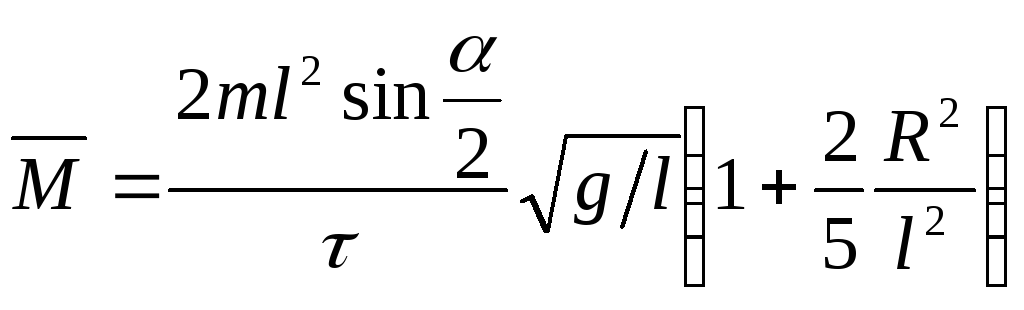
Определение средней силы взаимодействия соударяющихся шаров по радиусу площади их смятия в момент соударения

Постановка задачи. Определить среднюю длину взаимодействия шаров равной массы m₁=m₂=m, равного радиуса R_1`=R₂=R при упругом ударе. Угол начального отклонения правого шара равен , длины подвесов (до центра масс шаров) l₁=l₂=l, модули упругости материала шаров E₁=E₂=E, коэффициенты Пуассона ₁=₂=.

Указание к решению. В момент абсолютно упругого удара происходит смятие шаров за счет возникающих при ударе сил упругости (рис.8.3). Здесь R- радиус шаров, f-стрелка смятия, u=2f - сближение центров шаров в момент удара, 2а- диаметр площади смятия.

Из геометрических соображений (см. рис.8.3)

(8.18)

Учитывая, что угол  мал, оставляем лишь правые два члена в разложении

Из малости  следует также

Отсюда из (8.18) получим

(8.19)

Отметим, что соотношение (8.19) имеет смысл лишь при u<<R.

На площади смятия вследствие действия внешних сил возникает напряжение (сила, действующая на единицу площади)



Отсюда, используя известный закон Гука = / Е, получим выражение для относительной деформации  (рис.8.4):



Точнее, с учетом трехмерного обжатия со стороны недеформированных частей шара



где - коэффициент Пуассона. Стрелки смятия

f a. (8.20)

Используя выражение (8.19) и (8.20), определим размер радиуса смятия:

. (8.21)

Заметим, что точное выражение имеет вид

.

Отсюда можно оценить среднюю силу взаимодействия при ударе

Fa³ (8.22)

Указание: для получения отпечатка площади смятия между шарами следует вложить между ними папиросную бумагу с копировальной. Размеры отпечатка определяются с помощью специального микроскопа.

Проверка формулы Герца для соударяющихся упругих шаров

Постановка задачи. Применяя закон сохранения энергии в процессе соударения упругих шаров и учитывая нелинейный характер задачи (силы упругости растут с ростом радиуса смятия и с увеличением сближения шаров, Генрих Герц вывел соотношение (подробнее можно познакомиться с задачей Герца в книге[8]) между временем соударения и скоростью налетающего шара:   (1/)^1/5. Здесь - время соударения; - скорость налетающего шара.

Указания к решению. Скорость шара в момент начала соударения определяется из рис. 8.1. Задача решается с использованием закона сохранения энергии. Пусть в первый момент соприкосновения шаров механическая энергия . Тогда по мере взаимодействия и сближения шаров растет потенциальная энергия взаимодействия, а кинетическая энергия движущегося шара убывает. Из закона сохранения механической энергии имеем

(8.23)

Зависимость силы упругости от сближения шаров u получаем из (2.21)

F(-u3/2).

Из известного соотношения между потенциальной энергией и силой упругости

получим

W_потu^5/2; W_пот=ku^5/2. (8.24)

Здесь коэффициент пропорциональности k зависит от радиуса шаров и свойств материала. Из (8.23) и (8.24) получим уравнение

(8.25)

Максимальное сближение шаров достигается при du/dt0. Решив уравнение (8.25), определим время , в течение которого длится соударение (при этом u меняется от 0 до u_mas и обратно). Хотя уравнение (8.25) легко решается разделением переменных, закон Герца запишем без вывода

.

Здесь, как и ранее, коэффициент пропорциональности зависит от масс и размеров шаров, свойств материала. Для проверки закона Герца следует построить график, где по оси абсцисс отложить ₀, а по оси ординат произведение ²₀.

Указание: при малых углах  возможна замена sin. Отметим, что  надо рассчитать в радианах.