
- •Предисловие
- •Основы программирования
- •Понятие алгоритма.
- •Алгоритм Евклида.
- •Задача о поездах и мухе
- •Вместо лирического отступления
- •Этапы подготовки задачи для решения на компьютере
- •Примеры разработки алгоритмов
- •Решение квадратного уравнения.
- •Вычисление интегралов
- •Обработка результатов эксперимента
- •Решение системы линейных алгебраических уравнений
- •Введение в язык программирования Pascal
- •Основные элементы языка
- •Переменные. Стандартные типы.
- •Операции отношения
- •Раздел описаний переменных
- •Выражения. Порядок выполнения операций.
- •Константы
- •Комментарии в программе
- •Операторы
- •2.1.7.1. Оператор присваивания
- •2.1.7.2. Операторы ввода/вывода
- •2.1.7.3. Операторы инкремента и декремента
- •Среда разработки Lazarus
- •Русский язык в консольных приложениях
- •Первая программа
- •Открытие существующего проекта
- •Другие способы создания консольных приложений
- •Типовой пустой проект
- •Операции с целыми числами
- •Вместо лирического отступления 2
- •Стандартные функции с целыми аргументами
- •Операции с вещественными числами (тип real).
- •Форматирование вывода
- •Одновременное использование вещественных и целых чисел.
- •Другие стандартные функции с вещественными аргументами
- •Булевы переменные
- •Условные операторы.
- •2.1.22.1 Оператор if …. then
- •2.1.22.2. Оператор if …then ... else
- •Операторы цикла
- •2.1.23.1. Оператор цикла с предусловием
- •2.1.23.2. Оператор цикла с постусловием
- •2.1.23.3. Оператор цикла с параметром.
- •2.1.23.4. Второй вариант оператора цикла с параметром
- •Оператор выбора case
- •Организация простейшего контроля ввода данных.
- •Вычисление сумм сходящихся рядов
- •Реализация некоторых алгоритмов главы 1.
- •Программа решения задачи о поездах и мухе
- •Программа вычисления определенного интеграла
- •Более сложные элементы языка
- •Общая структура Паскаль – программы
- •Процедуры и функции
- •3.1.1.1 Структура процедуры
- •3.1.1.2. Структура функции
- •3.1.1.3 Глобальные и локальные переменные
- •3.1.1.4 Способы передачи параметров
- •3.1.1.5 Процедуры завершения
- •Еще раз о типах данных
- •Классификация типов данных
- •3.2.1.1 Целый тип
- •3.2.1.2. Интервальный тип
- •3.2.1.3. Перечислимый тип
- •3.2.1.4. Множества
- •3.2.1.5. Логический тип
- •3.2.1.6. Вещественный тип
- •3.2.1.7. Указатели
- •Обработка символьной информации в Паскале
- •Символьные и строковые типы данных.
- •3.3.1.1. Тип Char
- •3.3.1.2. Функции для работы с символами
- •3.3.1.3. Тип String
- •3.3.1.4. Строковые процедуры и функции
- •Массивы
- •Динамические массивы
- •Программа решения системы линейных алгебраических уравнений методом Гаусса
- •3.4.1.1. Вариант 1 – с goto
- •3.4.1.2. Вариант 2 – без goto
- •3.4.1.3. Вариант 3 – наилучшая реализация
- •Модули в Паскале
- •Структура модуля
- •Системные модули
- •3.5.2.1. Модуль CRT
- •Файлы
- •Тип данных – запись
- •Файловые типы
- •Процедуры для работы с файлами
- •3.6.3.1. Общие процедуры для работы с файлами всех типов
- •3.6.3.2. Процедуры для работы с текстовыми файлами
- •3.6.3.3. Процедуры для работы с типизированными файлами
- •3.6.3.4. Процедуры для работы с нетипизированными файлами
- •3.6.3.5. Организация контроля ввода/вывода при работе файлами
- •3.6.3.6. Создание простой базы данных с типизированными файлами.
- •Алгоритмы сортировки
- •Обменная сортировка (метод "пузырька")
- •Сортировка выбором
- •Сортировка вставками
- •Метод быстрой сортировки
- •Алгоритмы поиска
- •Поиск в массивах
- •Вставка и удаление элементов в упорядоченном массиве
- •Динамические структуры данных
- •Представление в памяти компьютера динамических структур.
- •Реализация стека с помощью массивов
- •Указатели
- •Стандартные операции с линейными списками
- •Реализация динамических структур линейными списками
- •4.3.6.1. Реализация стека
- •4.3.6.2. Реализация очереди с помощью линейного списка
- •4.3.6.3. Реализация двоичного дерева с помощью линейного списка
- •Сортировка и поиск с помощью двоичного дерева
- •Три источника и три составные части ООП.
- •Классы и объекты.
- •Обращение к членам класса.
- •Инкапсуляция
- •Спецификаторы доступа.
- •Свойства.
- •Наследование
- •Полиморфизм
- •Раннее связывание.
- •Позднее связывание.
- •Конструкторы и деструкторы.
- •Элементы графического интерфейса
- •Различия между консольными и графическими приложениями
- •Визуальное программирование в среде Lazarus
- •Создание графического приложения
- •Форма и ее основные свойства
- •Компоненты
- •Обработчики событий
- •Простейшие компоненты
- •6.3.5.1. Компонент TLabel
- •6.3.5.2. Кнопки TButton, TBitBtn и TSpeedButton
- •6.3.6.1. Компонент TEdit
- •6.3.6.2. Компонент TLabeledEdit
- •6.3.7.1. Компонент TMaskEdit
- •Специальные компоненты для ввода чисел
- •Тестирование и отладка программы
- •Компоненты отображения и выбора данных
- •6.3.10.1. Компонент TMemo
- •6.3.10.2. Компонент TStringGrid
- •6.3.10.3. Компоненты выбора
- •Компонент TListBox
- •Компонент TComboBox
- •Компоненты выбора – переключатели
- •6.3.10.4. Компоненты отображения структурированных данных
- •Компонент TTreeView
- •Компонент TListView
- •Организация меню. Механизм действий - Actions
- •6.3.11.1. Компонент TMainMenu
- •6.3.11.2. Компонент TToolBar
- •6.3.11.3. Компонент TActionList
- •6.3.11.4. Создание приложений с изменяемыми размерами окон
- •Послесловие
- •Литература
- •Алфавитный указатель
1.3 Примеры разработки алгоритмов
____________________________________________________________________
1.3.3 Обработка результатов эксперимента
При решении инженерных и экономических задач часто возникает необхо-
димость в получении математических зависимостей между различными пара-
метрами, характерными для данной задачи. Исходной информацией для уста-
новления этих зависимостей является физический эксперимент или экономиче-
ские показатели. Как в том, так и другом случае мы располагаем либо таблич-
ными данными, либо точками на графике. Пусть имеется зависимость Pi , полу-
ченная при дискретных значениях Z i . Значения Pi получены из эксперимента с некоторыми погрешностями. Требуется найти зависимость P 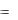 f (Z ) .
f (Z ) .
P
7
i
3
2
1
Z |
Z2 Z3 |
Zi |
Z7 |
Z |
1 |
|
|
|
Рис. 1.11. График функции
Учитывая, что P  f (Z ) имеет явно выраженную нелинейную зависимость,
f (Z ) имеет явно выраженную нелинейную зависимость,
запишем уравнение кривой второго порядка.
P X 0 X1Z X 2 Z 2 |
(1.13) |
В этом уравнении X 0 , X 1 , |
X 2 неизвестные пока коэффициенты. Для нахо- |
ждения этих коэффициентов запишем для всех имеющихся значений Pi зави-
симость вида (1.13).
P X |
0 |
X |
Z |
1 |
X |
2 |
Z 2 |
1 |
1 |
|
|
1 |
P X |
0 |
X |
Z |
2 |
X |
2 |
Z |
2 |
2 |
1 |
|
|
|
2 |
..………………
36

Глава 1 Основы программирования
____________________________________________________________________
P |
X |
|
X Z |
|
X Z |
2 |
||
i |
|
0 |
1 |
|
i |
2 i |
(1.14 |
|
|
|
|
||||||
……………………. |
||||||||
P |
X |
0 |
X |
Z |
7 |
X |
Z |
2 |
7 |
|
1 |
|
2 |
|
7 |
||
Получена система из 7 уравнений с 3 неизвестными. Необходимо таким
методом найти X 0 , X 1 , X 2 , чтобы зависимость (1.13) лучшим способом описала результаты, представленные на графике.
Для нахождения трех неизвестных предстоит решить систему из 7 уравне-
ний. Если мы отбросим какие-либо 4 лишних уравнений, мы найдем значения неизвестных без учета этих отброшенных уравнений. С другой стороны, систе-
ма (1.14) может быть несовместной, т.е. при ее решении мы можем не получить тождества и при подстановке найденных значений неизвестных в уравнения
системы получим разницу между левой и правой частями.
Обозначим |
эти разницы в соответствии с номерами уравнений через |
1 , 2 ... i ,..., 7 и |
будем называть их невязками. Невязка представляет собой |
разницу между аналитической зависимостью и значениями Pi , заданными в ка-
честве исходной информации в дискретных точках Z i .
Для того чтобы аналитическая зависимость наиболее полно отражала ре-
зультаты эксперимента, будем минимизировать величину:
7
S |
|
2 |
|
|
i |
|
|
|
|
(1.15) |
|
|
i 1 |
|
|
|
|
|
Невязки взяты в квадрат для того, чтобы любая невязка получалась с од-
ним положительным знаком, при этом соотношения малых и больших невязок увеличатся. Минимизация S будет выражать наилучшее приближение анали-
тической зависимости к экспериментальным точкам (при заданной степени по-
линома). Рассмотренный нами метод носит название метода наименьших квад-
ратов [3].
Общая формулировка задачи:
необходимо решить систему n-линейных уравнений с m неизвестными.
37
1.3 Примеры разработки алгоритмов
____________________________________________________________________
a11x1+a12x2+…+a1jxj+…a1mxm=b1 a21x1+a22x2+…+a2jxj+…a2mxm=b2
(1.16)
ai1x1+ ai2x2+…+aijxj +…aimxm =bi
……………………………………………………..
an1x1+an2x2+…+anjxj+…anmxm=bn
Запишем i-ое уравнение в более компактном виде:
|
|
m |
|
|
|
|
|
|
|
|
|
|
a ijxj = bi |
|
|
|
(1.17) |
||
|
|
j |
1 |
|
|
|
|
|
|
|
|
n |
n |
m |
|
|
|
|
|
тогда |
S |
2 |
( |
a |
ij |
x |
j |
b )2 |
(1.18) |
|
|
i |
|
|
|
i |
|
||
|
|
i 1 |
i 1 |
j 1 |
|
|
|
|
|
Для минимизации S возьмем от этой величины частные производные по каждой переменной xj и приравняем к 0.
s |
|
n |
m |
|
|
2 |
( |
aij x j bi )aij , |
(1.19) |
||
|
|||||
x j |
|||||
|
i 1 |
j 1 |
|
s0 , отсюда:
x j
n |
m |
|
( |
aij x j bi )aij 0 , |
(1.20) |
i 1 |
j 1 |
|
Таких уравнений будет столько, сколько неизвестных xj и получим систему n-линейных алгебраических уравнений с n неизвестными, которые решаются методом исключения с выделением главного элемента.
38
Глава 1 Основы программирования
____________________________________________________________________
1.3.4 Решение системы линейных алгебраических уравнений
Будем рассматривать систему из n уравнений с n неизвестными. Методы численного решения систем линейных уравнений подразделяются на две груп-
пы: прямые (конечные) и итерационные (бесконечные). Естественно, никакой практический метод решения не может быть бесконечным. Мы имеем в виду только то, что прямые методы могут в принципе (с точностью до ошибок ок-
ругления) дать такое решение, если оно существует, с помощью конечного чис-
ла арифметических операций. С другой стороны, при использовании итераци-
онных методов, для получения точного решения теоретически требуется беско-
нечное число арифметических операций. Значит, при практическом исследова-
нии итерационных методов появляются ошибки ограничения. Это не значит,
что прямые методы лучше, т.к. ошибки округления, появляющиеся в прямых методах, играют большую роль. В некоторых случаях из-за ошибок округления могут быть получены бессмысленные результаты. Несмотря на неизбежную ошибку ограничения, итерационные методы могут оказаться наиболее удобны-
ми, т.к. при его использовании ошибки округления не накапливаются.
Рассмотрим один из прямых методов называемых методом исключения
(метод Гаусса).
Для иллюстрации метода рассмотрим систему из 3 уравнений с 3 неиз-
вестными:
a11x1+a12x2+a13x3=b1 (1)
a21x1+a22x2+a23x3=b2 (2) (1.21) a31x1+a32x2+a33x3=b3 (3)
Здесь хотя бы один из коэффициентов a11, a21, a31 должен быть отличен от
0, иначе мы бы имели дело с 3 уравнениями с двумя неизвестными. Пусть a11≠0, если, это не так мы можем переставить местами уравнения, так чтобы ко-
39

1.3 Примеры разработки алгоритмов
____________________________________________________________________
эффициент при x1 в первом уравнении был отличен от 0. Перестановка уравне-
ний систему не изменит. Теперь введем множитель:
m2 |
a21 |
(1.22) |
|
a11 |
|||
|
|
Умножим 1-е уравнение (1.21) на m2 и вычтем его из 2-го уравнения (1.21).
Имеем:
(a21 |
m2a11)x1 |
(a22 |
|
m2a12 )x2 |
(a23 |
m2a13 )x3 |
b2 |
m2b1 |
(1.23) |
|||||
Но |
a |
|
m a |
a |
|
|
a21 |
a |
0 |
|
|
|
(1.24) |
|
|
|
|
|
|
|
|
||||||||
|
|
21 |
|
2 11 |
|
21 |
|
a11 11 |
|
|
|
|
|
|
Обозначим |
|
|
a22 |
|
a22 |
|
m2a12 |
|
|
|
|
|
||
|
|
|
|
a23 |
|
a23 m2a13 |
|
|
|
(1.25) |
||||
|
|
|
|
b2 |
b2 |
m2b1 |
|
|
|
|
|
|||
Тогда 2-е уравнение (1.21) приобретет вид:
a22 x2 a23 x3 b2 |
(1.26) |
Заменим это уравнение в (1.21) уравнением (1.26), получим систему:
a11x1+a12x2+a13x3=b1 |
(1) |
|
|||
a22 x2 |
a23 x3 |
b2 |
(4) |
(1.27) |
|
a31x1+a32x2+a33x3=b3 |
(3) |
|
|||
Умножим теперь (1) |
в (1.27) на m3 |
|
a31 |
и вычтем из (3) |
|
|
a11 |
||||
|
|
|
|
|
|
a32 |
a32 |
m3a12 |
|
|
|
40

Глава 1 Основы программирования
____________________________________________________________________
a33 a33 m3a13
b3 b3 m3b1
Уравнение (3) приобретает вид:
a32 x2 a33 x3 b3 |
(5) |
И исходная система (1.21) теперь имеет вид:
a11x1+a12x2+a13x3=b1 |
(1) |
|
||
a22 x2 |
a23 x3 |
b2 |
(4) |
(1.28) |
a32 x2 |
a33 x3 |
b3 |
(5) |
|
Эти новые уравнения эквивалентны исходным, с тем преимуществом, что |
||||
x1 не входит ни во второе, ни в третье уравнение системы. |
|
|||
Попытаемся теперь исключить x2 из уравнений (4) и (5). |
|
|||
Если a22 0 , то мы вновь снова переставим местами уравнения, так чтобы |
||||
a22 0 . Если же a22 |
0 и a32 |
0 , то система вырождена и либо не имеет ре- |
||
шения, либо имеет бесконечное множество решений. Введем новый множитель
m |
|
a3 2 |
. Умножим его на (4) и вычтем его из (5) |
|
3 |
a2 2 |
|
||
|
|
|
||
|
|
|
|
|
|
|
|
(a32 m3 a22 )x2 (a33 m3a23 )x3 b3 b2 m3 |
(1.29) |
В силу выбора m3
a32 m3 a22 0
a33 a33 m3 a23 |
(1.30) |
b3 b3 b2 m3
Уравнение (1.29) запишется в виде
41

1.3 Примеры разработки алгоритмов
____________________________________________________________________
a33 x3 b3 |
(1.31) |
Уравнение (1.29) можно заменить уравнением (1.31).
Система (1.21) приобретает вид:
a11x1+a12x2+a13x3=b1 |
(8) |
|
|
a22 x2 a23 x3 |
b2 |
(9) |
(1.32) |
a33 x3 |
b3 |
(10) |
|
Решение этой системы совершенно очевидно.
x3 |
b3 |
|
a33 |
||
|
|
|
|
x2 |
a23 x3 |
|
(1.33) |
|||
|
|
|
|
b2 |
|
||||
|
|
|
|
|
|
a22 |
|
||
|
|
|
x1 |
b1 |
a12 x2 a13 x3 |
|
|
||
|
|
|
|
a11 |
|
||||
|
|
|
|
|
|
|
|||
Для |
чего мы всегда переставляем уравнения таким образом, чтобы |
||||||||
a11, a22 , a33 |
были не равны 0? Чтобы не было деления на 0! |
|
|||||||
Пример: |
|
|
|
|
|
|
|
|
|
x |
y |
z |
4 |
|
|
|
|
|
|
2x |
3y |
|
z 9 |
|
|
|
(1.34) |
||
x |
y |
z |
2 |
|
|
|
|
|
|
Умножим первое уравнение (1.34) на 2 и вычтем из 2-го уравнения. Затем первое уравнение умножим на 1 и вычтем из 3-го. Получим систему, эквива-
42

Глава 1 Основы программирования
____________________________________________________________________
лентную (1.34).
x |
y |
z |
4 |
y |
z |
1 |
(1.35) |
|
2 y |
2z |
6 |
Умножив второе уравнение (1.35) на (-2) и вычтя его из 3-го уравнения получаем
x y z 4
y z 1 |
(1.36) |
4z  4
4
Отсюда решением этой системы будет: x 1
y 2 z 1
Обобщим этот метод на случай системы из n уравнений с n неизвестными
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
a21 x1 |
a22 x2 |
... |
a2n xn |
b2 |
(1.37) |
|
……………………………………………… |
|
|||||
an1 x1 |
|
an 2 x2 ... |
ann xn |
bn |
|
|
Предполагается в силу расположения уравнений a11 ≠0. Введем n-1 |
||||||
множителей: |
|
|
|
|
|
|
m |
ai1 |
, |
i = 1, 2, 3, … n |
(1.38) |
||
|
||||||
i |
a11 |
|
|
|
|
|
|
|
|
|
|
||
И вычтем из каждого i-го уравнения первое, умноженное на mi. Обозначим
aij aij mi a1 j ,
43

1.3 Примеры разработки алгоритмов
____________________________________________________________________
bi bi mi b1 |
, |
|
|
|
(1.39) |
|
i=2, 3, …, n, |
j=1, 2, …, n |
|
|
|||
Для всех уравнений, начиная со 2-го ai1 =0, i=2, 3, … n |
|
|||||
Получим систему |
|
|
|
|
|
|
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
0 a22 x2 |
... |
a2n xn |
b2 |
(1.40) |
||
……………………………………………… |
|
|
||||
0 |
an 2 x2 |
... |
ann xn |
bn |
|
|
Продолжая таким образом, мы можем исключить x2 из последних n-2
уравнений, x3 из последних n-3 уравнений и т.д. На некотором k-ом этапе мы исключим xk с помощью множителей.
|
(k 1) |
a (k 1) |
i=k+1,…n |
|
(1.41) |
|||
|
mi |
akk (k 1) , |
|
|||||
|
|
ik |
|
|
|
|
|
|
Причем |
|
|
|
|
|
|
|
|
a( k 1) |
0 , |
|
|
|
|
|
|
|
kk |
|
|
|
|
|
|
|
|
a(k ) |
a(k 1) |
m(k 1) a |
(k 1) |
|
|
|
|
|
ij |
ij |
i |
kj |
|
|
|
|
|
b( k ) |
b( k 1) |
m( k 1)b( k 1) |
|
|
|
|
||
i |
i |
i |
k |
|
|
|
|
|
где i = k+1, k+2,…, n; |
j = k,…, n; |
k = 1,…, n-1 |
|
|||||
Окончательно треугольная система уравнений записывается следующим |
||||||||
образом. |
|
|
|
|
|
|
|
|
|
|
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
|
|
|
a22 x2 |
... |
a2n xn |
b2 |
(1.42) |
|
44

Глава 1 Основы программирования
____________________________________________________________________
……………………….
|
|
|
|
|
|
|
|
|
|
|
|
a( n |
1) x |
|
b( n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
n |
n |
Обратная подстановка для нахождения значений неизвестных задается |
||||||||||||||||
формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
b( n |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a ( n |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b( n 2) |
a( n |
2) |
|
x |
|
|
|
|
|
|
|
|
||
xn 1 |
|
|
n 1 |
n 1,n |
|
|
n |
|
|
|
|
|
(1.43) |
|||
|
|
|
|
a( n 2) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n 1,n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
b( j |
1) |
|
a( j 1) |
x |
j |
|
|
... a( j 1) |
x |
j 1 |
|
|
|
|
|
x j |
j |
|
|
j ,n |
|
|
|
j , j 1 |
|
, |
j=n-2, n-3,…,1 |
|||||
|
|
|
|
|
a jj |
( j 1) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
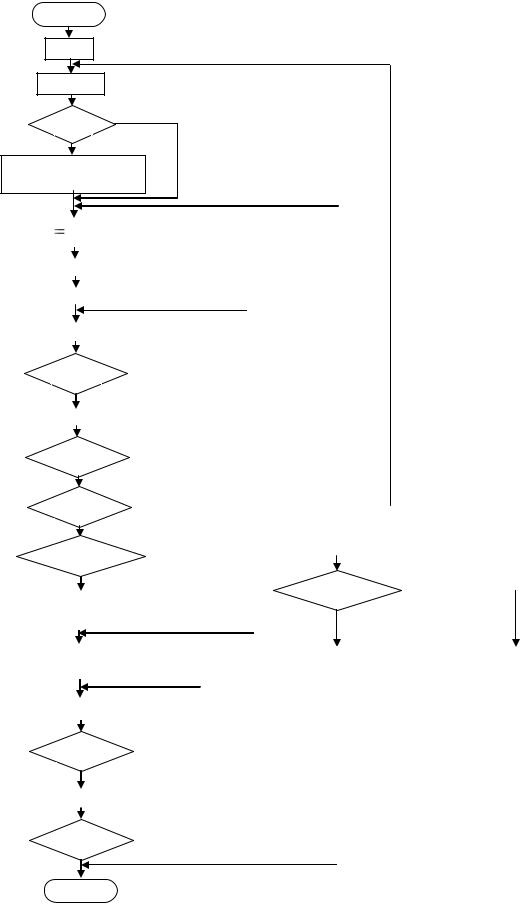
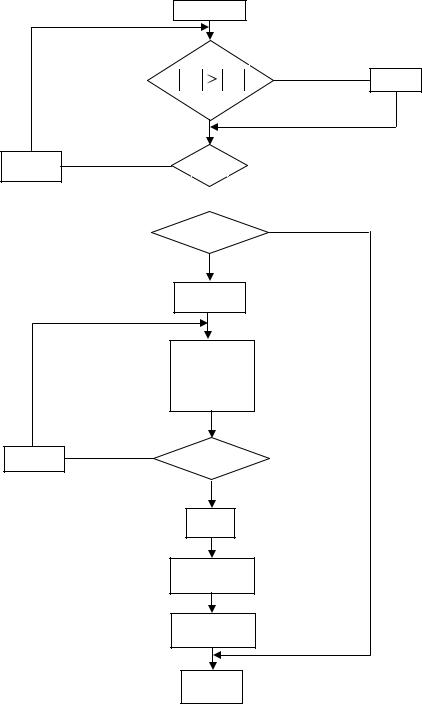
Блок-схема алгоритма показана на рис. 1.12.
Здесь, чтобы не загромождать блок-схему, мы предположили, что коэффи-
циенты системы уже введены. В этой блок-схеме неясно только одно – что зна-
чит переставить уравнение, как это сделать?
Оказывается, что если переставить уравнения таким образом, чтобы коэф-
фициент при xk был наибольшим, то ошибки округления будут минимальными.
Этот коэффициент называется главным элементом. И перестановка уравнений c
выбором главного элемента называется методом главных элементов, рис. 1.13.
45
1.3 Примеры разработки алгоритмов
____________________________________________________________________
начало
k=1
i=k+1
нет
akk=0
да
Переставить ур-е так чтобы akk≠0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m aik / akk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aik=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
j=k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aij=aij-makj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
j=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
j=j+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
bi=bi-mbk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
i=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i+1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
да |
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
k=n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=k+1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ann=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn=0 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
xn=bn/ann |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
i=n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=i+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система не |
|
|
|
Система имеет бесконеч- |
|||||||||||
|
|
|
|
|
|
|
|
S=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет решения |
|
|
|
ное множество решений |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S=S - aijxj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
j=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=j+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
xi=(bi + S)/aii |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конец |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.12. Алгоритм Гаусса |
|
|
|
|||||||||||
46
Глава 1 Основы программирования
____________________________________________________________________
i=i+1
j=j+1
l=k
|
да |
aik alk |
l=i |
нет
нет
i=n
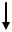
 да
да
l=k
да
нет
j=k
t=akj
akj=alj
alj=t
нет
j=n
да
t=bk
bk=bl
bl=t
i=k+1
Рис. 1.13. Алгоритм перестановки уравнений
47
