
- •Предисловие
- •Основы программирования
- •Понятие алгоритма.
- •Алгоритм Евклида.
- •Задача о поездах и мухе
- •Вместо лирического отступления
- •Этапы подготовки задачи для решения на компьютере
- •Примеры разработки алгоритмов
- •Решение квадратного уравнения.
- •Вычисление интегралов
- •Обработка результатов эксперимента
- •Решение системы линейных алгебраических уравнений
- •Введение в язык программирования Pascal
- •Основные элементы языка
- •Переменные. Стандартные типы.
- •Операции отношения
- •Раздел описаний переменных
- •Выражения. Порядок выполнения операций.
- •Константы
- •Комментарии в программе
- •Операторы
- •2.1.7.1. Оператор присваивания
- •2.1.7.2. Операторы ввода/вывода
- •2.1.7.3. Операторы инкремента и декремента
- •Среда разработки Lazarus
- •Русский язык в консольных приложениях
- •Первая программа
- •Открытие существующего проекта
- •Другие способы создания консольных приложений
- •Типовой пустой проект
- •Операции с целыми числами
- •Вместо лирического отступления 2
- •Стандартные функции с целыми аргументами
- •Операции с вещественными числами (тип real).
- •Форматирование вывода
- •Одновременное использование вещественных и целых чисел.
- •Другие стандартные функции с вещественными аргументами
- •Булевы переменные
- •Условные операторы.
- •2.1.22.1 Оператор if …. then
- •2.1.22.2. Оператор if …then ... else
- •Операторы цикла
- •2.1.23.1. Оператор цикла с предусловием
- •2.1.23.2. Оператор цикла с постусловием
- •2.1.23.3. Оператор цикла с параметром.
- •2.1.23.4. Второй вариант оператора цикла с параметром
- •Оператор выбора case
- •Организация простейшего контроля ввода данных.
- •Вычисление сумм сходящихся рядов
- •Реализация некоторых алгоритмов главы 1.
- •Программа решения задачи о поездах и мухе
- •Программа вычисления определенного интеграла
- •Более сложные элементы языка
- •Общая структура Паскаль – программы
- •Процедуры и функции
- •3.1.1.1 Структура процедуры
- •3.1.1.2. Структура функции
- •3.1.1.3 Глобальные и локальные переменные
- •3.1.1.4 Способы передачи параметров
- •3.1.1.5 Процедуры завершения
- •Еще раз о типах данных
- •Классификация типов данных
- •3.2.1.1 Целый тип
- •3.2.1.2. Интервальный тип
- •3.2.1.3. Перечислимый тип
- •3.2.1.4. Множества
- •3.2.1.5. Логический тип
- •3.2.1.6. Вещественный тип
- •3.2.1.7. Указатели
- •Обработка символьной информации в Паскале
- •Символьные и строковые типы данных.
- •3.3.1.1. Тип Char
- •3.3.1.2. Функции для работы с символами
- •3.3.1.3. Тип String
- •3.3.1.4. Строковые процедуры и функции
- •Массивы
- •Динамические массивы
- •Программа решения системы линейных алгебраических уравнений методом Гаусса
- •3.4.1.1. Вариант 1 – с goto
- •3.4.1.2. Вариант 2 – без goto
- •3.4.1.3. Вариант 3 – наилучшая реализация
- •Модули в Паскале
- •Структура модуля
- •Системные модули
- •3.5.2.1. Модуль CRT
- •Файлы
- •Тип данных – запись
- •Файловые типы
- •Процедуры для работы с файлами
- •3.6.3.1. Общие процедуры для работы с файлами всех типов
- •3.6.3.2. Процедуры для работы с текстовыми файлами
- •3.6.3.3. Процедуры для работы с типизированными файлами
- •3.6.3.4. Процедуры для работы с нетипизированными файлами
- •3.6.3.5. Организация контроля ввода/вывода при работе файлами
- •3.6.3.6. Создание простой базы данных с типизированными файлами.
- •Алгоритмы сортировки
- •Обменная сортировка (метод "пузырька")
- •Сортировка выбором
- •Сортировка вставками
- •Метод быстрой сортировки
- •Алгоритмы поиска
- •Поиск в массивах
- •Вставка и удаление элементов в упорядоченном массиве
- •Динамические структуры данных
- •Представление в памяти компьютера динамических структур.
- •Реализация стека с помощью массивов
- •Указатели
- •Стандартные операции с линейными списками
- •Реализация динамических структур линейными списками
- •4.3.6.1. Реализация стека
- •4.3.6.2. Реализация очереди с помощью линейного списка
- •4.3.6.3. Реализация двоичного дерева с помощью линейного списка
- •Сортировка и поиск с помощью двоичного дерева
- •Три источника и три составные части ООП.
- •Классы и объекты.
- •Обращение к членам класса.
- •Инкапсуляция
- •Спецификаторы доступа.
- •Свойства.
- •Наследование
- •Полиморфизм
- •Раннее связывание.
- •Позднее связывание.
- •Конструкторы и деструкторы.
- •Элементы графического интерфейса
- •Различия между консольными и графическими приложениями
- •Визуальное программирование в среде Lazarus
- •Создание графического приложения
- •Форма и ее основные свойства
- •Компоненты
- •Обработчики событий
- •Простейшие компоненты
- •6.3.5.1. Компонент TLabel
- •6.3.5.2. Кнопки TButton, TBitBtn и TSpeedButton
- •6.3.6.1. Компонент TEdit
- •6.3.6.2. Компонент TLabeledEdit
- •6.3.7.1. Компонент TMaskEdit
- •Специальные компоненты для ввода чисел
- •Тестирование и отладка программы
- •Компоненты отображения и выбора данных
- •6.3.10.1. Компонент TMemo
- •6.3.10.2. Компонент TStringGrid
- •6.3.10.3. Компоненты выбора
- •Компонент TListBox
- •Компонент TComboBox
- •Компоненты выбора – переключатели
- •6.3.10.4. Компоненты отображения структурированных данных
- •Компонент TTreeView
- •Компонент TListView
- •Организация меню. Механизм действий - Actions
- •6.3.11.1. Компонент TMainMenu
- •6.3.11.2. Компонент TToolBar
- •6.3.11.3. Компонент TActionList
- •6.3.11.4. Создание приложений с изменяемыми размерами окон
- •Послесловие
- •Литература
- •Алфавитный указатель

1.3 Примеры разработки алгоритмов
____________________________________________________________________
1.3. Примеры разработки алгоритмов
1.3.1 Решение квадратного уравнения.
Найти корни квадратного уравнения AX2+BX+C=0, коэффициенты A, B, C за-
даны и вводятся с клавиатуры.
Из элементарной математики известна формула для нахождения корней этого уравнения:
X1,2 |
B B 2 4 AC |
, |
(1.8) |
|
2 A |
||||
|
|
|
Однако эта формула применима только для случая действительных корней.
Но мы считаем, что коэффициенты A, B, C могут быть произвольными, поэтому необходимо произвести анализ задачи и определить возможные варианты вы-
числений. Анализ задачи и определение возможных ситуаций, возникающих в ходе вычислений, является одной из важнейших функций программиста. По-
пытка запрограммировать только формулу (1.8) может привести к неопреде-
ленной ситуации, если A=0, или B2-4AC<0. Именно программист должен преду-
смотреть возможность возникновения таких ситуаций и явным образом указать порядок вычислений в каждом конкретном случае.
Если A=0, это означает, что исходное уравнение выродилось в линейное
BX+C=0. В этом случае решением его будет
X |
B |
, |
(1.9.) |
|
C |
||||
|
|
|
Если дискриминант B2-4AC<0, уравнение будет иметь комплексные со-
пряженные корни. Каждое комплексное число можно представить парой дейст-
вительных чисел, одно из которых изображает действительную часть, другое -
мнимую часть комплексного числа.
Действительные части обоих корней равны.
Re X1 Re X 2 |
B |
, |
(1.10) |
|
2A |
||||
|
|
|
32
Глава 1 Основы программирования
____________________________________________________________________
А мнимые будут иметь разные знаки, и вычисляться по формуле
Im X 1 |
(B 2 |
4 AC) |
|
, |
|
|
|
Im X |
|
|
Im X1 , |
(1.11) |
||||||||||
|
2 A |
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
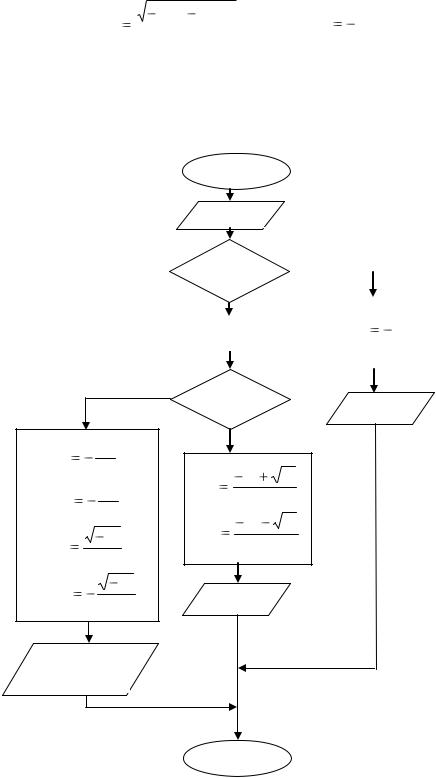
Исходя из этих рассуждений, нетрудно составить блок-схему алгоритма |
||||||||||||||||||||||
вычисления корней квадратного уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
начало |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
A, B, C |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
D=B2-4AC |
|
|
|
|
|
X |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
C |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
D<0 |
|
|
|
|
|
X |
||
|
|
|
|
|
|
|
B |
|
|
нет |
|
REX1 |
|
|
|
|
|
2 A |
|
|
|
|
|
|
|
|
B |
D |
|
|
B |
X1 |
|||
REX 2 |
2 A |
|
|||
2 A |
|
|
|
||
|
|
|
B |
D |
|
|
D |
X |
|
||
IMX1 |
2 |
2 A |
|
||
2 A |
|
|
|
||
|
|
|
|
|
|
IMX 2 |
D |
|
|
|
|
2 A |
X1, X2 |
|
|||
|
|
||||
|
|
|
|
|
|
ReX1, ReX2, |
|
|
|
|
|
ImX1, ImX2 |
|
|
|
|
|
конец
Рис. 1.9. Алгоритм вычисления корней квадратного уравнения
33

1.3 Примеры разработки алгоритмов
____________________________________________________________________
1.3.2 Вычисление интегралов
b
Вычислить интеграл f (x)dx по формуле Симпсона с точностью 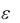 10 5 .
10 5 .
a
Формула Симпсона, как известно, имеет вид [1,2]:
b |
b a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
( y |
|
y |
|
2( y |
|
y |
|
... y |
|
) 4( y |
y |
|
... y |
|
)) |
, |
(1.12) |
|
|
0 |
n |
2 |
4 |
n 2 |
3 |
n 1 |
||||||||||||
|
n 3 |
|
|
|
|
1 |
|
|
|
|
|
||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для достижения требуемой точности применим метод двойного пересчета,
суть которого заключается в следующем. Пусть n=4 – число точек разбиения интервала (a, b).
Вычисляем интеграл I4. Затем увеличиваем n в два раза, (n=8) и вычисляем
I8.
Если |I4-I8|≤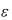 ,то требуемая точность достигнута. В качестве результата бе-
,то требуемая точность достигнута. В качестве результата бе-
рем I8. Если же |I4-I8|> 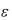 , то снова увеличиваем n в два раза (n=16) вычисляем I16,
, то снова увеличиваем n в два раза (n=16) вычисляем I16,
затем если |I8-I16|≤ , то точность достигнута. Если нет, то повторяем вышеука-
, то точность достигнута. Если нет, то повторяем вышеука-
занный процесс до достижения требуемой точности. Блок-схема алгоритма вы-
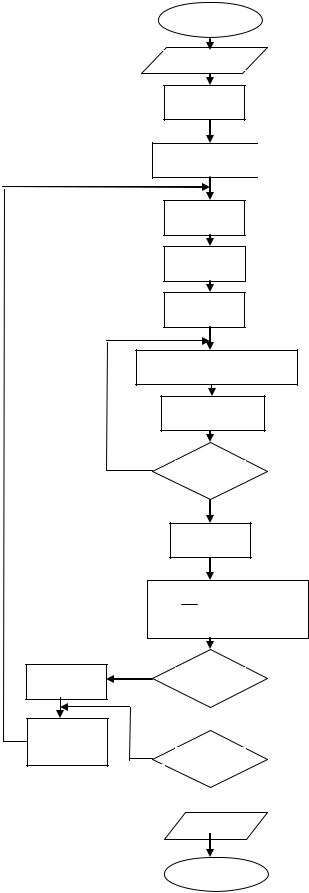
числения интеграла по формуле Симпсона методом двойного пересчета будет выглядеть следующим образом:
34
Глава 1 Основы программирования
____________________________________________________________________
K=1
S1=S
H=H/2
Начало
A, B, N, 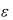
K=0
H=(B-A)/N 

X=A
X=X+H
S=0
S=S+f(x)+2f(X+H)
X=X+2H
да
X<B-H
нет
S=2S
S= H3 (f(A)+f(B)+S)
нет
K=1
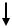
 да
да
|S1-S|≤ 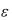

нет
 да
да
S
Конец
Рис.1.10. Алгоритм вычисления определенного интеграла по формуле Симпсона
35
