Учебник

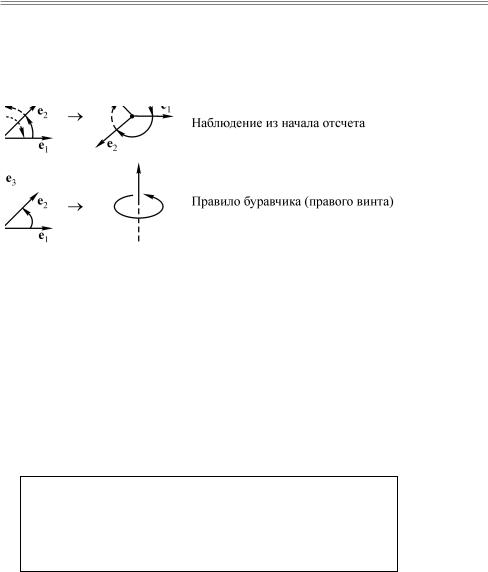
5. Системы координат

дать наименования этим базисам. Для этого удобно использовать понятия правого и левого базиса, которые мы использовали на плоскости и на прямой (где эти названия очевидны).

Ðèñ. 5.10. Определения правого базиса

Ввиду того, что зачастую представление трехмерных фигур вызывает некоторые трудности, мы приведем три определения правого базиса, которые наиболее часто используются.

Определение 13а

Базис в пространстве называется правым (базисом с правой ориентацией), если при наблюдении с конца третьего вектора поворот от первого вектора ко второму происходит против часовой стрелки.

Если совместить концы базисных векторов в начале отсчета — точке О, то можно представить себе, что точка О является вершиной пирамиды, ребрами которой являются три базисных вектора. Тогда наблюдение со стороны точки О помогает дать еще одно определение базиса с правой ориентацией.

73

I. Векторная алгебра

Определение 13б

Базис в пространстве называется правым, если при наблюдении из начала координат повороты от первого вектора ко второму, от второго к третьему и от третьего к первому происходят по часовой стрелке.

Однако наиболее часто употребляется третье определение базисов с правой ориентацией, известное как «правило буравчика» или «правило правого винта». Особенно часто это правило используется в физике, так как с помощью него определяют направление силы, действующей со стороны магнитного поля на движущиеся электрические заряды.

Определение 13в

Базис в пространстве называется правым, если при вращении правого винта от первого базисного вектора ко второму этот винт закручивается в направлении третьего базисного вектора.

Самым простым методом определения ориентации базиса является, по-видимому, знакомое всем из школьного курса физики правило правой руки. Согласно этому правилу порядок векторов в правом базисе соответствует порядку пальцев правой руки — большого, указательного и среднего при их определенном расположении.

Как мы уже говорили, существует простой способ определения того, имеют ли два базиса одинаковую ориентацию. Для этого достаточно попытаться совместить их непрерывными движениями — параллельным переносом и вращением — в пространстве. Если удается найти движение, совмещающее эти базисы, то они имеют одинаковую ориентацию. В противном случае базисы принадлежат к разным ориентациям и для их совмещения необходимо хотя бы один из векторов базиса поменять на противоположный ему вектор. В ка- честве примера можно взять базисы (e1,e2 ) è (e5 ,e6 ) на рис.5.8 или базисы (e1,e2 ,e3 ) è (e4 ,e5 ,e6 ) на рис.5.9. Таким образом, существуют такие преобразования базисов, которые не меняют их ориентации. Эти преобразования называются собственными пре-

74

5. Системы координат

образованиями. Преобразования, которые изменяют ориентацию базиса, называются несобственными. Более подробно собственных и несобственных преобразований, а также численного описания мы коснемся позже в разделе о преобразованиях координат.

Понятие ориентации можно применить не только к ортонормированным базисам, но и к любым упорядоченным тройкам векторов. Действительно, все определения ориентации не содержат информации о длине векторов и углах между ними. Поэтому можно ввести понятие ориентированных троек векторов.

Определение 14

Правой (левой) тройкой векторов называется тройка некомпланарных векторов, имеющих правую (левую) ориентацию.

Конечно, определить, имеют ли различные тройки векторов одинаковую ориентацию с помощью их совмещения, уже не удастся, потому что в эти тройки могут входить векторы с разными длинами, и углы между векторами в этих тройках могут быть неодинаковыми.

5.7. Типичные задачи

Задача 5.1. Определить вектор скорости точки при равномерном вращении.

Решение. Предположим, что точка вращается по окружности с постоянным радиусом R и угловой скоростью ω. Радиус-век- тор этой точки равен r = rer = Rer , а скорость равна производной от радиус-вектора по времени:

v = ddtr = d(dtRer ) = dRdt er + R ddter = R ddter .

В последнем преобразовании учитывается, что радиус вращения не меняется со временем. Орт er зависит от положения

75

5. Системы координат

Это выражение определяет как величину линейной скорости вращения v = Rω , так и направление v ↑↑eϕ , то есть скорость направлена по касательной к окружности, по которой вращается точка.

Задача 5.2. Найти расстояние между точками в полярной сис-

N = (rN ,ϕ N ). Расстояние между ними выражается через декартовы координаты:

MN = (xM − xN )2 +( yM − yN )2 .

Для использования этой формулы нам достаточно выразить декартовы координаты точек через полярные с помощью соотношений x = r cosϕ è y = r sinϕ. Подстановка этих выражений в формулу для длины MN äàåò:

MN = (xM − xN )2 +( yM − yN )2 =

=(rM cosϕ M 1 −rN cosϕ N )2 +(rM sinϕ M − rN sinϕ N )2 =

=rM2 + rN2 − 2rM rN (cosϕ M cosϕ N +sinϕ M sinϕ N ) =

= rM2 + rN2 −2rM rN cos(ϕ M −ϕ N ).

Полученное соотношение есть не что иное, как теорема косинусов, и приведенный вывод может рассматриваться как доказательство теоремы косинусов с помощью координатного метода. В то же время, это соотношение можно переписать другим способом, явно выделив квадрат разности длин радиус-векторов и слагаемое, которое мало, если мал угол между радиус-векторами:

77

6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

6.1. Угол между векторами

Мы ввели понятие векторов как множества равных между собой направленных отрезков. При этом некоторые свойства отрезков удалось обобщить и для векторов. К таким свойствам, например, относится длина или сумма направленных отрезков. Оказывается, на векторы можно обобщить и такое понятие, как угол между направленными отрезками.

Ðèñ.6.1. К обоснованию определения угла между векторами

Предположим, нам даны два вектора a è b. Если от заданной точки O1 отложить два отрезка, соответствующих этим векторам O1 A1 = a è O1B1 = b, то угол между этими направленными отрезками будет равен α1 = A1O1B1. Причем, для однозначности договоримся, что в качестве угла α1 выбирается наименьший из углов A1O1B1 è 360°− A1O1B1.

79

I. Векторная алгебра

Если мы теперь отложим такие же направленные отрезки O2 A2 = a è O2 B2 = b от другой точки O2 , то методами элементарной геометрии (см. рис. 6.1) можно доказать, что угол

α 2 = A2O2 B2 равен углу α1.

Следовательно, понятие угла между направленными отрезками можно обобщить на векторы, образованные этими отрезками, следующим образом:

Определение 15

Угол между ненулевыми векторами — это угол между проведенными из общего начала направленными отрезками, соответствующими этим векторам.

(a,b) = AOB, ãäå OA = a è OB = b.

Ðèñ. 6.2. Угол между векторами

Но можно сделать и наоборот. А именно — спроектировать вектор a на вектор b (получится ортогональная проекция Prba = ON) и тогда тот же угол будет вычисляться по другой формуле:

80

6. Скалярное произведение векторов

Сравнивая между собой эти две формулы, замечаем, что они переходят друг в друга, если вектор a поменять местами с вектором b. Естественно, такой симметрией обладает не только косинус угла между векторами cos( (b,a)) = cos( (a,b)), но и некоторые другие комбинации, такие, как ba = ab и тому подобные. В частности, широкое применение в математике и физике нашла следующая симметричная комбинация, содержащая оба вышеприведенных соотношения:

ab cos( (a,b)) = ba cos( (b,a)).

Для этой комбинации было придумано специальное обозначе- ние a b и наименование — скалярное произведение векторов.

Изучим теперь эту операцию подробнее на тривиальном примере одномерного пространства.

6.2. Произведение векторов в одномерном пространстве

Простейшим пространством, которое мы рассмотрели, является прямая. Прямую можно рассматривать как одномерное пространство, и все векторы, параллельные одной прямой, после задания базиса можно описывать одной координатой. В этом случае возникает однозначная связь между векторами и вещественными числами. Каждый вектор соответствует вещественному числу, которое является его координатой: a = (a). Сложение векторов будет происходить так же, как и обычное сложение чисел. Например, вектор c = (5) с координатой 5 можно представить в виде суммы векторов c = a +b = (2) + (3) = (5) с координатами 2 и 3 так же просто, как и представить число 5 в виде суммы чисел 2 и 3. Однако для чисел, кроме операции сложения, есть еще и операция умножения. Результатом произведения чисел является также вещественное число.

81

I. Векторная алгебра

Оказывается, операция умножения вещественных чисел так же может быть перенесена на векторы, как и сложение. Мы можем назвать произведением двух коллинеарных векторов операцию, результатом которой является произведение координат этих векторов. Например, для уже рассмотренных выше векторов a = (2) è b = (3) результатом их произведения будет число 6, равное обычному произведению координат этих векторов

(6 = 2 3) :

Для произвольных коллинеарных векторов a = (a1 ) è b = (b1 ) определение произведения можно записать в следующем виде:

При этом аналогия произведения векторов и чисел не является полной, как в случае сложения. Дело в том, что если результатом сложения и умножения чисел является число, а сумма векторов — это также вектор, то результатом произведения векторов является обычное число, а не какой-нибудь другой вектор. Эта особенность определила название такого умножения векторов — скалярное произведение, то есть произведение, результатом которого является не векторная, а скалярная величи- на. Определение скалярных величин и их отличие от векторов мы рассмотрим позднее при изучении преобразований базисов и систем координат.

Скалярное произведение имеет глубокие физические аналогии. Если на тело действует сила F и под действием этой силы тело перемещается вдоль направления ñèëû F на величину r = r (òî åñòü r || F), то работа, совершаемая этой силой, равна как раз скалярному произведению силы на перемещение A = F r ≡ F r. В этом соотношении F è r — не величины векторов, а их координаты.

Аналогично это и в изотропных средах, когда векторы электрической и магнитной напряженностей и индуктивностей сонаправлены, плотности энергии электрического UE и магнитного полей UM находятся по формулам, которые содержат скалярное

82