Учебник

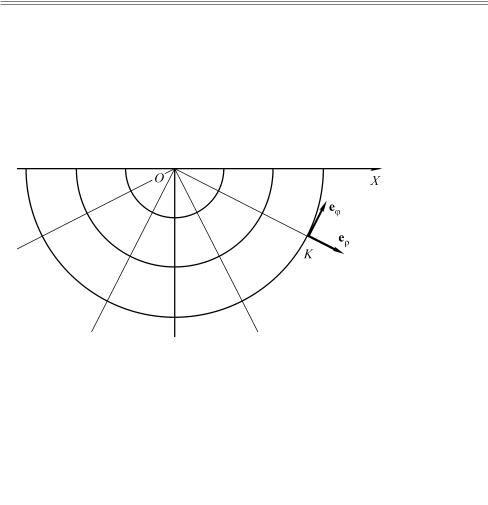
5. Системы координат

Такой выбор угла может оказаться удобным при исследовании поворотов на большие углы, в частности — при исследовании вращений.

Ðèñ. 5.4. Координатные кривые и орты в полярной системе отсчета

Если использовать понятие радиус-вектора точки М, то для полярных координат этой точки получаются следующие соотношения:

63

I. Векторная алгебра

Здесь ab — угол между векторами a è b, определение которого будет дано в следующем разделе.

Для однозначности определения угла ϕ добавим условие:

которое, аналогично (5.4), позволяет задать такую область изменения полярного угла: 0 <ϕ < 2π .

Определим тип кривых, вдоль которых постоянны значения координат, то есть построим линии уровня. В случае постоянного радиуса получаем окружности с центром в начале координат (см. рис.5.4), а при постоянном полярном угле такими линиями являются лучи, идущие от начала отсчета. Эти линии уровня образуют своеобразную сетку на плоскости, причем через любую точку в пространстве проходит ровно по одной линии уровня, соответствующей каждой из координат. В этом смысле картина очень похожа на декартову систему (см. рис.5.2). Более того, как и в декартовой системе координат, в полярной системе линии уровня, соответствующие различ- ным координатам, перпендикулярны между собой. Таким образом, полярная система отсчета — так же как и декартова — является прямоугольной (или ортогональной системой отсчета).

Однако, в отличие от декартовой системы, в полярной системе линиями уровня являются не прямые, а лучи и окружности. Поэтому такая система относится к так называемым криволинейным системам отсчета.

Кроме того, возникает вопрос о том, куда направлены базисные векторы в полярной системе отсчета. В случае с радиальной координатой этот вектор направляется вдоль луча, идущего из

начала координат, то есть eρ = rr , а значит, этот орт фактически

является ортом радиус-вектора.

А вот направление орта, соответствующего полярному углу eϕ , можно выбрать, исходя из ортогональности полярных координат. Это значит, что этот орт должен быть перпендикулярен орту радиальной координаты, который направлен вдоль радиуса. Следова-

64

5. Системы координат

тельно, орт угловой переменной eϕ можно направить вдоль касательной к окружностям, причем, в соответствии с определением 11а, направляем его в сторону увеличения полярного угла. Таким образом, мы получаем еще одно обобщение понятия орта.

Определение 11б

В прямоугольных криволинейных системах координат орты направлены по касательным к координатным линиям в сторону роста соответствующей координаты.

На рис. 5.4 показаны орты в полярной системе отсчета, отложенные от разных точек.

Мы видим, что орты в полярной системе координат имеют существенное отличие от ортов в декартовой системе. Их направление зависит от точки наблюдения! Этот факт необходимо учитывать при решении физических задач, то есть учитывать что, например, при движении частицы в пространстве меняются не только ее полярные координаты, но и полярные орты.

Простейшим примером является равномерное вращение точ- ки по окружности, которое будет рассмотрено в одной из задач в конце раздела.

5.3. Цилиндрическая система координат

Простейшим обобщением полярной системы координат в трехмерном пространстве является цилиндрическая система отсчета. В этой системе для определения положения точки добавляется третья координата, характеризующая «высоту», на которой находится точка. Цилиндрические координаты можно ввести следующим образом. Вначале зададим некую декартову систему отсчета, в которой точка имеет координаты M = (x, y, z), а затем опустим перпендикуляр из точки M на плоскость xOy. Основанием этого перпендикуляра будет некоторая точка M1 с координатами M1=(x, y, 0). Положение этой точки на плоскости xOy можно задавать в полярной системе отсчета, то есть M = (ρ,ϕ ,0). Набор из трех чисел — радиуса ρ, полярного угла ϕ и аппликаты z будет

65

I. Векторная алгебра

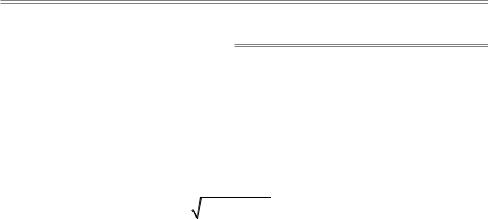
однозначно описывать положение в пространстве исходной точки M = (ρ,ϕ , z) Эти координаты называются цилиндрическими. Это связано с тем, что координатными поверхностями, соответствующими радиусу ρ, то есть поверхностями, у всех точек которых эта координата одинакова, являются цилиндры. Цилиндрические координаты используются при решении задач, в условии которых присутствует выделенная ось, зачастую являющаяся осью симметрии исследуемой системы. К таким системам, например, относятся системы, в которых задан ток, текущий по центральному проводнику или системы, в которых задано внешнее, постоянное в пространстве, поле.

Связь декартовых и цилиндрических координат (учитывая, что третья координата в этих системах одинакова), получается прямо аналогичной связи полярных и декартовых координат (5.1) и (5.2):

Ðèñ. 5.5. Цилиндрическая система координат

66

5. Системы координат

5.4. Сферическая система координат

Более последовательным обобщением полярной системы от- счета для трехмерного случая является так называемая сфери- ческая система отсчета. Она вводится, когда мы хотим в качестве одной из координат выбирать, как и в случае с полярной системой, расстояние от точки до начала отсчета, то есть — длину радиус-вектора точки:

Тогда координатной поверхностью, соответствующей этой координате (радиусу), то есть поверхностью, вдоль которой не меняется эта координата, а именно не меняется расстояние от точек до начала отсчета, является сфера с центром в начале отсчета. Для того чтобы различать точки, на этой сфере, вводят угол между радиус-вектором и осью аппликат Оz, который показывает, насколько точка отклонилась от вертикального положения:

Заданным значениям этих двух координат будет соответствовать множество точек, а именно — окружность в горизонтальной плоскости и центром на оси Оz. Для того, чтобы различать точки на этой окружности, поступим следующим образом. Проведем луч из начала координат в точку наблюдения. Построим ортогональную проекцию этого луча на плоскость xOy и определим в качестве координаты угол между этим лучом-проекцией и осью абсцисс Ox также, как и в полярной системе координат. Таким образом, третья координата будет определяться следующим выражением:

которое для однозначности определения угла дополняется условием, аналогичным (5.6). Напомним, что величина Prexey r обозначает проекцию вектора r на плоскость, образованную векторами ex è ey .

67

I. Векторная алгебра

Введенные таким способом координаты называются сферичес-

кими и однозначно определяют положение точки в пространстве

M = (ρ,θ ,ϕ ).

Соотношения (5.9)–(5.11) позволяют определить связь между декартовыми и сферическими координатами:

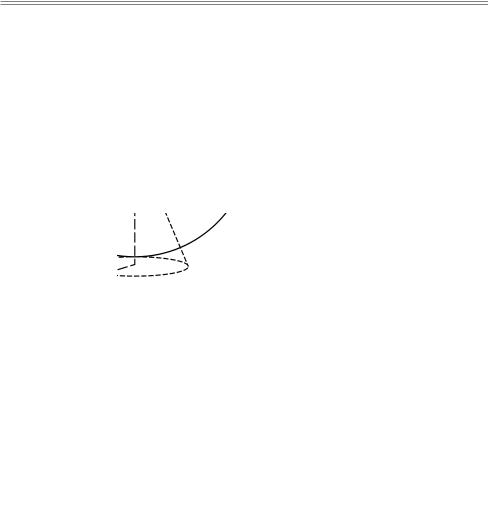
Ðèñ. 5.6. Сферическая система координат. Координатные поверхности и орты

Сферическая система координат так же, как полярная и цилиндрическая системы, является криволинейной и ортогональной системой. На рис. 5.6 приведены примеры координатных поверхностей в сферической системе координат. Постоянному значению радиуса соответствуют сферы с центром в начале отсчета. Если определить множество точек, у которых одинаков угол ϕ , òî ïî-

68

5. Системы координат

лучим полуплоскости, края которых совпадают с осью Oz. Постоянному значению угла θ соответствует конус, вершина которого находится в начале отсчета.

В сферической системе отсчета из-за ее криволинейности направление ортов зависит от точки наблюдения. Поэтому равные направленные отрезки, отложенные от разных точек пространства, будут иметь разные координаты в сферической системе координат, хотя их длины и направления будут совпадать. Так, если орт ey отложить от точки наблюдения, которая находится на оси абсцисс (точка К на рис. 5.6), то он будет в сферической системе отсчета иметь координаты ey = (0,1,0), а если этот же орт отложить от точки на оси ординат (например, точка L на рис. 5.6), то его сферические координаты станут равными ey = (1,0,0). В то же время сферическая система является ортонормированной и поэтому длина любого вектора, заданного своими координатами

aρ = aeρ , aθ = aeθ è aϕ = aeϕ ,

но при этом векторы a è âñå îðòû e берутся в точке наблюдения. Основное применение сферическая система отсчета находит в задачах движения частиц в полях, обладающих центральной симметрией, то есть в полях, у которых величина поля зависит только от расстояния до заданного центра. Это, например, гравитационное

или электростатическое поле сферически симметричной частицы.

5.5. Базисы и системы отсчета различной ориентации

Рассмотренные нами декартова, полярная, цилиндрическая и сферическая системы отсчета не исчерпывают всего многообразия ортогональных систем. Для того чтобы разобраться в том, каким

69

I. Векторная алгебра

еще образом системы могут отличаться друг от друга, рассмотрим простейший пример одномерного пространства — прямой.

Проведем прямую λ и выберем на ней базис (e1 ), состоящий, естественно, из одного вектора e1. Наряду с этим базисом мы

противоположно направленный векторам e1 è e2.

Мы замечаем, что все базисы на прямой могут быть разделены на две группы, каждая из которых содержит базисы, векторы которых направлены в одну сторону. Принадлежность базиса к той или другой группе называется ориентацией базиса. В частности, на горизонтальной прямой удобно все базисы, векторы которых направлены вправо, называть правыми базисами (или базисами с правой ориентацией), а базисы, векторы которых направлены влево — левыми базисами (или базисами с левой ориентацией). Например, приведенные на рис. 5.6 базисы e1 è e2 являются базисами правой ориентации, а e3 è e4 — базисами левой ориентации.

(e1 ) и (e2 ) — базисы правой ориентации (e3 ) и (e4 ) — базисы левой ориентации

Ðèñ. 5.7. Базисы различной ориентации на прямой

Если мы рассмотрим только ортонормированные базисы, то основное правило, дающее ответ на вопрос, имеют ли два ортонормированных базиса одинаковую ориентацию, может быть сформулирован так:

Ортонормированные базисы одинаковой ориентации могут быть совмещены движениями внутри пространства, в котором они определены.

Так, базис (e1 ) на рис. 5.7 может быть совмещен с базисом (e5 ), а базис левой ориентации (e3 ) никаким движением нельзя вдоль прямой перевести в базисы (e1 ) èëè (e5 ).

70

5. Системы координат

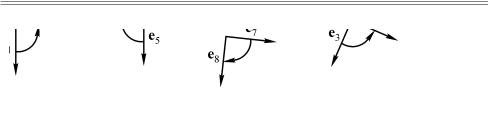
Базисы (e1,e2 )и (e3 ,e4 )— базисы правой ориентации Базисы (e5 ,e6 ) и (e7 ,e8 )— базисы левой ориентации

Ðèñ. 5.8. Базисы различной ориентации на плоскости

Теперь рассмотрим различные ортонормированные базисы на плоскости. На рис. 5.8 приведены примеры базисов (e1,e2 ),

(e3 ,e4 ), (e5 ,e6 ) è (e7 ,e8 ). Мы видим, что некоторые из этих базисов могут быть совмещены между собой с помощью дви-

жений вдоль плоскости, то есть движений, переводящих плоскость саму в себя. К таким движениям относятся параллельный перенос и повороты вокруг какой-нибудь оси, перпендикулярной плоскости. На рисунке видно, что базисы (e1,e2 ), (e3 ,e4 ) могут совместиться так, чтобы и первые, и вторые векторы базисов совпали между собой. Можно совместить между

собой и базисы (e5 ,e6 ) è (e7 ,e8 ).

В то же время, никакими перемещениями, не выходящими из плоскости, нельзя совместить, например, базис (e1,e2 )и базис (e7 ,e8 )так, чтобы вектор e1 совпал с вектором e7 , а вектор e2 —

с вектором e8.

Мы видим, что и на плоскости все базисы могут быть разделены на две группы: одни аналогичны базису (e1,e2 ), а другие — базису (e7 ,e8 ). Принадлежность базиса к какой-то из этих групп называется так же, как и в одномерном случае, ориентацией базиса. Названия ориентаций остаются такими же, как и в одномерном случае — правая и левая. Однако на плоскости эти названия не так очевидны, как на прямой, поэтому необходимо различным ориентациям дать соответствующие определения.

71

I. Векторная алгебра

Определение 12

На плоскости базисом с правой ориентацией называется базис, в котором первый базисный вектор может быть совмещен со вторым поворотом против часовой стрелки в сторону меньшего угла.

В левых базисах первый вектор совмещается со вторым если его вращать в сторону меньшего угла по часовой стрелке.

Заметим, что понятие ориентации возникло только после того, как мы ввели упорядочение базиса, то есть стали отличать, какой из векторов базиса первый, а какой — второй.

В трехмерном пространстве базисы также делятся на две группы, отличающиеся своей ориентацией. Для того чтобы понять различие между ними, выберем на плоскости два двумерных базиса с одинаковой ориентацией (см. рис. 5.9) — правые базисы (e1,e2 ) è (e4 ,e5 ).

Базис (e1,e2 ,e3 ) — базис правой ориентации Базис (e4 ,e5 ,e6 )— базис левой ориентации

Ðèñ. 5.9. Базисы различной ориентации в пространстве

Теперь добавим к этим базисам по одному некомпланарному им вектору, чтобы получить базисы для трехмерного пространства. Причем к первому базису (e1,e2 ) добавим третий вектор e3 , который направлен в одну сторону от исходной плоскости, а к другому базису добавим третий вектор e6 , направленный в другую сторону от этой плоскости.

Мы получили различные базисы — их нельзя совместить друг с другом никакими движениями в пространстве. Теперь можно

72