Учебник

8. Смешанное и двойное векторное произведение векторов

((a ×b) ×c)y = (a ×b)z cx −(a ×b)x cz = (a ×b)z cx = axbycx ,

Как видно, координаты векторов в (ДВП 3.2) и (ДВП 3.3) совпадают, а значит, и сами векторы равны:

(a ×b) ×c = b(ac) −a(bc). ■

Существует еще более лаконичный вид второго доказательства, то есть доказательства с помощью координат. Это доказательство хорошо тем, что только оно может быть применено в многомерных векторных пространствах (размерности больших трех) при раскрытии формул аналогичных (a ×b) ×c.

Доказательство 4

Воспользуемся определением векторного произведения через символ Леви-Чивита. Тогда двойное векторное произведение может быть записано в виде:

133

I. Векторная алгебра

В последнее выражение входит произведение тензоров Леви- Чивита, которое равно

i=3

∑εijk εimn =δ jmδ km −δ jnδ km. i=1

Используя это соотношение, для исходного произведения (a ×b) ×c получаем

(a ×b) ×c = ∑ anbmcjek (δ jmδ km −δ jnδ km ) = i, j,k ,m,n

= ∑(ajbk cjek −akbjcjek ) = b(ac) −a(bc). j,k

Здесь мы использовали известные выражения:

Ключевым для данного доказательства является соотношение для произведения символов Леви-Чивита. Это соотношение можно проверить простым перебором всех компонент. ■

Отметим еще раз, что особенностью последних трех доказательств является необходимость привлечения координатного представления векторов. В то же время, даже согласно своему определению векторное произведение полностью определено и в том случае, когда не введена какая бы то выло система координат. Значит, должны существовать доказательства соотношения (a ×b) ×c = b(ac) −a(bc), исходящие из определений векторного и скалярного произведений. Вот одно из таких доказательств, любезно предоставленное автору учебника студентом ФТФ ХНУ Голубовым А. А.:

Доказательство 5

1.Приведем только идею доказательства для одного частного случая. Остальные варианты расположения векторов рассматриваются аналогичным образом.

2.Представим вектор c в виде суммы двух слагаемых c = c|| +c , первое из которых компланарно векторам a è b, а второе ортогонально этим векторам. Тогда в двойном векторном произведении останется только компонент c|| :

134

8. Смешанное и двойное векторное произведение векторов

(a ×b) ×c = (a ×b) ×(c|| +c ) = (a ×b) ×c||. (ÄÂÏ 5.1)

В качестве примера рассмотрим одно возможное взаимное расположение трех векторов a, b è c|| на плоскости, которой они компланарны.

Ðèñ. 8.2. К доказательству 5

Векторы a è b образуют некоторый базис на этой плоскости. Потому вектор (a ×b) ×c = OD можно разложить по этим векторам:

Для вычисления коэффициентов разложения опустим из точ- ки D перпендикуляр на прямую OA и отметим точку E — основание этого перпендикуляра. Тогда величина

Умножим это соотношение на sinα и исключим из него величину OB sinα с помощью равенства (ДВП 5.3):

OA sinα = OD (cosγ sinα −sin γ cosα )= OD sin(α −γ ). (ÄÂÏ 5.6)

135

I. Векторная алгебра

Задача 8.3 (продолжение задачи 6.1). Найти компонент вектора a, ортогональный вектору b ≠ 0.

Решение. В задаче 6.1 был найден компонент a|| вектора α , параллельный ненулевому вектору b :

= (ab) a|| b (bb) .

136

8. Смешанное и двойное векторное произведение векторов

Отсюда можно найти компонент a вектора a, перпендикулярный вектору b :

= − (ab) a a b (bb) .

Теперь приведем правую часть этого выражения к общему

В числителе стоит не что иное, как двойное векторное произведение (b ×a) ×b. Значит, искомое выражение для a выглядит так:

a == (b ×a) ×b) . (bb)

Задача 8.4 (окончание задачи 8.2). Упростить выражение

((b ×c),(c ×a),(a ×b)) = (b ×c) ×(c ×a) (a ×b).

Решение. Для решения задачи рассмотрим двойное векторное произведение (b ×c) ×(c ×a), где в качестве первого вектора возьмем (b ×c), второго — c, а третьего — a.

Тогда:

(b ×c) ×(c ×a) = c((b ×c) a) −a(c (b ×c)) = c(a,b,c).

Умножая это произведение на (a ×b), получаем:

(a ×b) c(a,b,c) = (a,b,c) (a,b,c) = (a,b,c)2 .

Таким образом, мы показали, что некомпланарность векторов a ×b, b ×c è c ×a эквивалентна некомпланарности векторов a, b è c, òî åñòü:

((b ×c),(c ×a),(a ×b)) = (a,b,c)2 .

137

I. Векторная алгебра

Решение. Величина (a ×b) (c ×d) представляет собой смешанное произведение трех векторов (a ×b,c,d). Следовательно, в нем можно переставить знаки местами:

(a ×b) (c ×d) = {(a ×b) ×c} d.

В фигурных скобках стоит двойное векторное произведение, которое раскрываем согласно правилу:

{(a ×b) ×c} d ={b(ac) −a(cb)} d.

Раскрывая фигурные скобки, окончательно получаем искомое соотношение:

è d совпадают:

(a ×b) (a ×b) = (aa)(bb) −(ab)(ab).

Это соотношение связывает длины векторного и скалярного произведения двух векторов:

(a ×b)2 = a2b2 −(ab)2 .

Причем последнее соотношение может быть доказано прямо из определений длин векторного и скалярного произведения:

(a ×b)2 = a 2 b 2 sin2 ( ab) = a 2 b 2 − a 2 b 2 cos2 ( ab).

138

9. ПРЕОБРАЗОВАНИЯ СИСТЕМЫ КООРДИНАТ

Мы рассмотрели различные ортогональные системы координат — декартовы, полярные, сферические и цилиндрические. При этом одной из наших задач было определение связи между координатами в различных системах. Знание таких связей позволяет подбирать для решения задач такие системы отсчета, в которых решение существенно упрощается. Ведь зачастую условия даются

âтаких системах отсчета, в которых сама задача выглядит просто, а решение при этом принципе возможно, но оказывается слишком громоздким.

Для физики классическим примером такого перехода является переход от лабораторной системы отсчета, в которой покоящийся наблюдатель производит измерения начальных условий, к системе центра инерции взаимодействующих тел,

âкоторой производятся расчеты. При решении различных задач математической физики или в квантовой механике постоянно используются переходы между различными базисами, в которых базисным векторам соответствуют не только обычные пространственные координаты, но и различные математические функции или квантовые состояния физических систем.

При исследовании различных реакций координатами могут быть количества того или иного реагента, поэтому такие координаты называются естественными. В то же время расчет таких реакций удобно проводить в других координатах, которые в некотором смысле ортогональны между собой, и поэтому называются нормальными.

140

9. Преобразования систем координат

Даже в компьютерной и телевизионной технике применяется преобразование координат. Дело в том, что цветное изображение на экране монитора, телевизора или в памяти компьютера нужно представлять в координатах, определяющих количество красного, синего и зеленого цветов. В тоже время при переносе этого изображения на бумагу требуется переход в другую систему отсчета — а именно в систему, в которой каждый цвет определяется количеством желтой, голубой и пурпурной красок, необходимых для точной передачи этого цвета.

Ðèñ. 9.1. Координаты одного и того же вектора в различных системах координат

Этот пример нам кажется наиболее интересным, поэтому ему будет посвящен отдельный раздел в этом учебнике. А пока мы вернемся к преобразованию координат в декартовых системах отсчета.

9.1. Вектор и точка в различных системах отсчета

Представим, что на плоскости задан некоторый вектор a единичной длины. Предположим, что на плоскости заданы три различные системы координат, K, K ′, K ′′, повернутые друг относительно друга на 45 градусов (см. рис. 9.1). Тогда в системе отсчета K этот вектор будет иметь координаты x =1 è y = 0. В системе отсчета K′ его координаты будут совсем другие x′ = 0

141

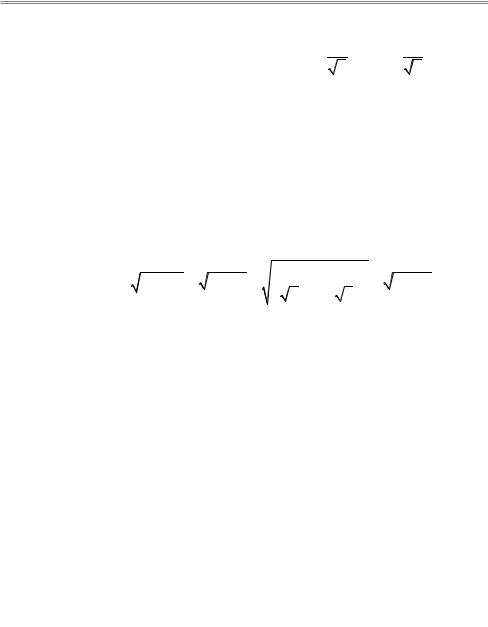
I. Векторная алгебра

è y′ = −1. А в системе отсчета K′′ у этого же вектора вообще не будет равных нулю координат: x′′ = 12 è y′′ = 12 . Â òî æå

время сам вектор как геометрический или физический объект не изменился: он так и остался нарисованн на том же месте.

Таким образом, вектор — это нечто большее, чем абстрактный набор чисел, размещенных по порядку внутри скобок. Этот набор чисел должен содержать в себе информацию о каком-то объекте, который существует вне зависимости от того, какая система отсчета выбрана и выбрана ли она вообще.

В качестве примера рассмотрим длину вектора, которая оказывается неизменной, в какой бы из систем координат мы ее не вычисляли:

Другое свойство вектора — направление — также должно определяться координатами. Следовательно, для того, чтобы координаты в различных системах отсчета определяли вектор одного и того же направления, они должны быть однозначно связаны между собой, причем по какому-то строго определенному закону. В этом разделе мы займемся выводом такого закона преобразования координат.

Ðèñ. 9.2. Координаты одной и той же точки в различных системах координат

142