
Учебник
.pdf
4. Размерность пространства. Понятие базиса
На рис. 4.1 показаны примеры проекций вектора на базисные векторы. Основным и самым полезным из свойств проекций является то, что любой вектор может быть представлен в виде суммы проекций на различные подпространства заданного пространства. Например, вектор a = a1e1 + a2e2 + a3e3 может быть записан такими способами:
a = Pr a + Pr a + Pr a = a1e1 |
+ Pr |
|
,e3 |
= |
||
e1 |
e2 |
e3 |
e2 |
(4.5) |
||
= a2e2 |
+ Pr |
= a3e3 + Pr |
. |
|
||
|
|
|||||
|
e1,e3 |
|
e1,e2 |
|
|
|
Другие два свойства проекций уже относятся к линейным операциям над векторами, которые проецируются. Эти свойства представлены в следующей теореме, а доказательство ее мы оставим для самостоятельной работы.
Теорема 10
Проекция суммы векторов равна сумме проекций этих векторов, а проекция произведения вектора на число равна произведению этого числа на проекцию этого вектора:
Pr(a +b) = Pra + Prb ;
Prλa = λ Pra .
Доказательство
Пусть даны два вектора a = a1e1 + a2e2 + a3e3 è b = b1e1 +b2e2 +b3e3.
Найдем их проекции Pre ,e |
a è Pre ,e b, проекцию их суммы |
|||
Pre2 |
2 |
3 |
2 |
3 |
,e3 (a +b) на подпространство, образованное векторами e2 |
||||
è e3 |
. По определению, эти проекции будут составлены из тех |
|||
слагаемых в разложениях векторов по базису, которые содержат векторы e2 è e3. Òî åñòü
Pr |
,e3 |
a = a2e2 |
+ a3e3 |
, à Pr |
b = b2e2 +b3e . |
(Ò 10.1) |
e2 |
|
|
e2 |
,e3 |
|
Сумма этих векторов равна
53

I. Векторная алгебра
Pr |
,e3 |
a + Pr |
b = a2e2 + a3e3 +b2e2 +b3e . |
(Ò 10.2) |
e2 |
e2 |
,e3 |
|
Теперь возьмем вектор суммы
a +b = (a1 +b1 )e1 + (a2 +b2 )e2 + (a3 +b3 )e3
и построим его проекцию на подпространство, образованное векторами e2 , e3 :
Pr |
(a +b) = (a2 +b2 )e2 +(a3 +b3 )e3 . |
(Ò 10.3) |
e2 |
,e3 |
|
Так как правые части соотношений (Т 10.2) и (Т 10.3) равны друг другу, то и левые также оказываются равными. Следовательно, теорема доказана. ■
Одной из особенностей такого ведения проекций является их необязательная ортогональность. Однако далее в нашем курсе мы будем иметь дело лишь с частным видом проекций, — ортогональной проекцией. То есть, при геометрическом построении проекции одного вектора а на другой вектор ñ будем опускать перпендикуляр от концов вектора ñ на прямую, заданную другим вектором а. Например: Prac = b ↔ b 
 a , а разность c −b a.
a , а разность c −b a.
Однако, для использования понятия ортогональных проекций нам необходимо еще ввести понятие угла между векторами, что мы сделаем в соответствующем разделе.

5. СИСТЕМЫ КООРДИНАТ
5.1. Определение системы координат. Радиус-вектор
Мы уже ввели понятия базиса в векторном пространстве и координат векторов в заданном базисе. Координатное представление оказалось удобным алгебраическим представлением векторов, которое позволило отказаться от графического изображения векторов как направленных отрезков и перевело операции над векторами на алгебраический язык.
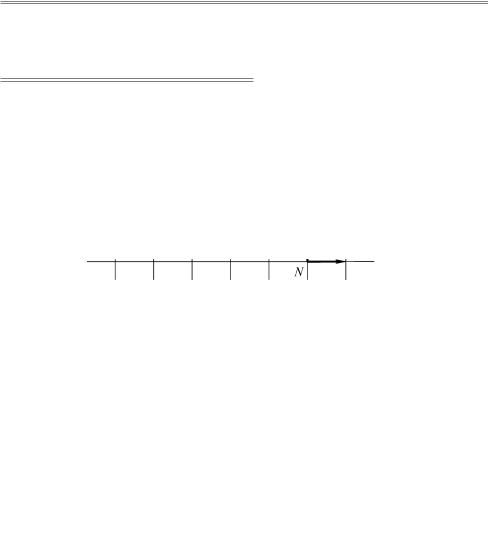
Теперь выберем в обычном пространстве точку O и отложим от нее направленные отрезки, соответствующие векторам векторного пространства, например, OM = a. Концы этих отрезков являются точками в обычном пространстве, причем разным векторам будут соответствовать разные точки. В свою очередь, если выбрана точка O, то любая другая точка пространства определяет вектор в векторном пространстве, который называется ра- диус-вектор и имеет обозначение. Например, радиус-вектор точки N обозначается как
rN = ON. |
(5.1) |
Таким образом, можно говорить о взаимнооднозначном соответствии векторов и точек в соответствующих пространствах, если задана некоторая начальная точка. Но в этом случае каждой точке в пространстве можно поставить в соответствие набор из координат вектора, который соответствует этой точке. И эти
55

I. Векторная алгебра
числа будут однозначно определять эту точку так же, как они однозначно определяют этот вектор. Набор этих чисел будем называть координатами точки. Обозначать тот факт, что точка M имеет координаты a1, a2 è a3 (для примера рассмотрим трехмерное пространство) будем следующим образом: M (a1, a2 , a3 ), или по аналогии с векторами так: M = (a1, a2 , a3 ).
Описание точек с помощью координат — так называемый координатный метод — позволяет, с одной стороны, полностью отказаться от геометрических построений при решении геометрических задач. С другой стороны, при решении задач в сложных алгебраических пространствах или сложных физических системах этот метод позволяет применять интуитивно понятные образы, такие как прямые, плоскости и т. п.
Введем основные понятия координатного метода. Так как точ- ка O соответствует нулевому вектору OO = 0, то все ее координаты будут нулевыми O = (0,0,0), поэтому ее принято называть
началом отсчета.
Наличия начала отсчета и базиса достаточно, чтобы каждой точке пространства сопоставить ее координаты, поэтому совокупность начала отсчета и базиса называется системой координат.
Кривые, состоящие из точек, среди координат которых есть только одна ненулевая, например M = (0,0, a3 ), называются координатными осями. Эти оси естественным образом направлены вдоль одного из базисных векторов.
Поверхности, состоящие из точек, среди координат которых есть две ненулевые, например M = (a1,0, a3 ), называются координатными поверхностями. Эти плоскости параллельны плоскостям, образованным соответствующими базисными векторами. Кривые (поверхности), вдоль которых одна из координат не меняется, называются линиями (поверхностями) уровня, соответствующего этой координате.
Приведем пример двумерной системы координат. На рис. 5.1 обозначено начало отсчета — точка O, базисные векторы e1 = OA è e2 = OB, координатные оси OC è OD. На этих осях с помощью стрелок обязательно указывается направление, в котором растет соответствующая координата. Так, первая координата точ-
56

5. Системы координат
êè C, равная трем, больше первой координаты точки A, равной единице.
На рисунке для примера нанесены точки с определенными координатами. Первая координата точки M равна 2, а вторая — 1. Это обозначается как M = (2,1). А, например, точка N имеет координаты –1 и 2, что обозначается следующим образом N = (−1, 2). На рисунке нанесены также радиус-векторы этих точек — rM = OM è rN = ON, которые, в соответствии с их определением, имеют такие же координаты, как и точки, которым они соответствуют: rM = OM = (2,1) è rN = ON = (−1, 2).
Ðèñ. 5.1. Пример системы координат
На рисунке проведены и линии уровня. Например, если двигаться вдоль прямой AF, то первая координата не будет меняться. Таким образом, эта прямая является линией уровня для первой координаты. Примером кривых уровня для второй координаты является прямая BM .
В системах координат линиями уровня являются прямые, поэтому такие системы называются прямолинейными.
57
I. Векторная алгебра
5.2. Декартов базис. Прямоугольные системы координат. Декартова система координат
Среди множества базисов можно выделить базисы, в которых базисные векторы перпендикулярны друг другу и имеют единич- ную длину. Например, в двухмерном случае это базис
|
|
|
|
e ,e |
, |
ãäå |
|
|
|
e |
|
= |
|
e |
2 |
|
=1 |
è e |
e |
; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
( 1 |
|
2 ) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|||
а в трехмерном случае это базис |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
e ,e |
2 |
,e |
, |
ãäå |
|
e |
|
= |
|
e |
2 |
|
= |
|
e |
3 |
|
=1 è |
e |
e |
2 |
, |
e |
2 |
e |
3 |
è e |
3 |
e |
. |
||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
( 1 |
|
3 ) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|||||||
Ðèñ. 5.2. Декартова система координат на плоскости
Такие системы называются прямоугольными или ортогональными и имеют собственное название: декартовы системы координат. Длина базисных векторов в таких системах координат равна единице, поэтому эти векторы являются ортами. Декартовы системы координат чаще всего применяются при решении ма-
58
5. Системы координат
тематических и физических задач, поэтому координаты в такой системе имеют собственные обозначения — x, y, z — и наименования — абсцисса, ордината и аппликата соответственно.
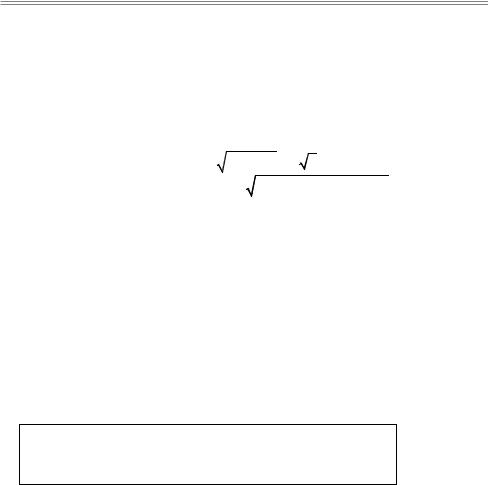
Главным удобством применения декартовых систем координат является простота формулы для вычисления расстояния между двумя точками (или длины вектора) с помощью теоремы Пифагора. Для примера рассмотрим точки на рис.5.2 Длина направлен-
ного отрезка OM равна |
OM |
= xM2 |
+ yM2 = 2 5. А расстояние |
||||
между точками A è B равно |
|
AB |
|
= |
(xA − xB )2 +( yA − yB )2 = 5. |
||
|
|
||||||
Второе преимущество этой системы — независимость ортов от точки пространства. Например, орты, построенные из точки N (рис. 5.2), совпадают с ортами, построенными из точки O. Это совершенно естественно. Ведь от точек O è N мы откладываем направленные отрезки, соответствующие одним и тем же векторам — ортам базиса. До сих пор мы изучали векторные пространства и базисы в векторном пространстве, поэтому у нас не возникало понятия точки и понятия орта, отложенного от ка- кой-то точки. Теперь мы перешли к изучению систем координат на множестве точек (например, на плоскости или в пространстве). На таких множествах понятие орта несколько обобщается и имеет следующий вид:
Определение 11а
Орт — единичный вектор базиса, направленный в сторону увеличения соответствующей координаты.
Заметим, что в прямоугольных системах координат такое определение дает те же орты ex è ey , которые получаются, если мы сначала вводим ортонормированный базис в двумерном векторном пространстве, а затем, выбрав в пространстве начало от- счета, получаем однозначное соответствие между точками этого пространства и векторами в векторном пространстве.
Если мы изначально работаем с каким-то множеством точек, то вполне может случиться так, что нам удобно ввести координаты, которые будут однозначно описывать местоположение точек, но при этом не будут соответствовать координатам каких-либо
59

I. Векторная алгебра
векторов в каком-нибудь векторном пространстве. К таким системам, в частности, относятся полярная, цилиндрическая и сферическая системы координат.
5.3.Полярная система координат
Âдекартовых системах отсчета две разные точки отличаются друг от друга своими декартовыми координатами. То есть смысл координатного метода заключается в том, что о местоположении точек можно судить не из графических построений, а из сравнений между собой чисел. Это, как мы не раз уже говорили, является одной из основных задач аналитической геометрии.
При решении некоторых прикладных задач выбор декартовых координат не является самым лучшим. Например, при изучении вращения по окружности с постоянным радиусом различные положения вращающейся точки отличаются друг от друга лишь углом поворота. Поэтому математически проще будет решать такую задачу не в декартовых переменных, а задавая в качестве координаты угол поворота. Этот угол тогда будет единственной меняющейся величиной.
С другой стороны, существует большое количество систем, обладающих так называемой центральной симметрией, при которой состояние системы определяется только расстоянием от некоторого центра и не зависит от углов поворота. В этом случае достаточно одной переменной — расстояния от точки до центра — для полного описания решения задач, а переход к двум декартовым только усложнит рассмотрение.
Однако, в общем случае, расстояние от точки до центра не полностью характеризует местоположение точки. Например, на
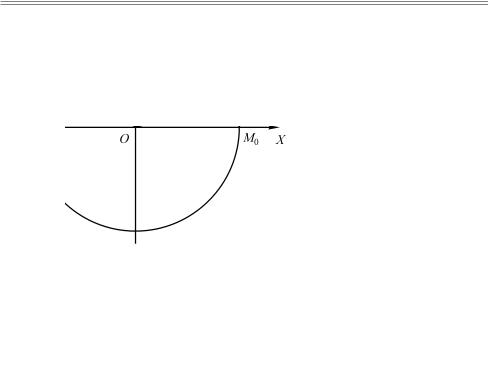
рис.5.3 изображены две различные точки M1 è M2, которые находятся на одинаковом расстоянии от начала отсчета — точки O, а следовательно, лежат на одной окружности с центром в точке О. Для того, чтобы описать математически различное местоположение этих точек, необходимо указать, где на окружности находятся эти точки. В частности, эти точки можно было бы различать длиной дуги между этими точками и некоторой начальной точкой,
60
5. Системы координат
например точкой М0, которая является пересечением окружности и оси абсцисс. Эти два числа — радиус и длина дуги — однозначно определяли бы положение точки и поэтому вполне бы подошли на роль координат. Эти координаты имели бы одинаковую размерность и этим были похожи на декартовы.
Ðèñ. 5.3. Полярная система координат
Однако, общепринятым является другой подход. В качестве второй координаты выбирают не длину дуги, а ее угловую величину.
Например, для точки М1 |
|
вторая координата равна ϕ1 |
= M0OM1. |
|||||||
Заметим, что этот угол может быть связан (хотя и не всегда) |
||||||||||
с длиной дуги |
|
M0 M1 |
|
по известной формуле ϕ1 |
= |
|
M0M1 |
|
|
. |
|
|
|
|
|||||||
|
|
|||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ρ |
|||
|
|
|
|
|
||||||
Таким образом, набор из двух чисел — расстояние до центра и угол между лучом, идущим от центра к точке, и каким-то заданным лучом, — может служить координатами для точек на плоскости. Такие координаты называются полярными координатами. Для полного определения таких координат нужно задать на плоскости начало от- счета — полюс, некоторый луч — полярный луч, и направление отсче- та угла, например против хода часовой стрелки. Если мы изначально имели некоторую декартову систему отсчета, то в качестве полюса
61
I. Векторная алгебра
принято выбирать начало отсчета — точку О, а в качестве луча — полуось Ох, соответствующую положительным значениям абсцисс.
В этом случае можно написать соотношения между декартовыми и полярными координатами:
x = ρ cosϕ
, (5.1)
y = ρ sinϕ
ρ
ϕ
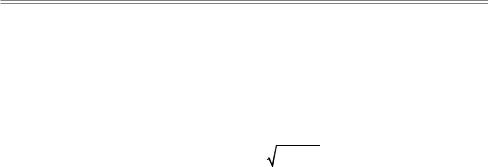
= x2 + y2 |
|
||
|
y . |
(5.2) |
|
= arctg |
|
|
|
|
|
||
|
x |
|
|
Мы видим, что полученные соотношения однозначно определяют только тангенс полярного угла. Следовательно, сам угол будет определен с точностью до 180 градусов. Поэтому соотношений (5.2) не хватает для определения угла, потому что если мы возьмем вместо х и у противоположные им значения, то получим те же значения tgϕ.
Таким образом, для однозначного определения полярных координат надо дополнить соотношения (5.2) еще каким-то соотношением, учитывающим знак координат x è y. Например, если
область значений |
функции |
|
arctgα |
определена |
неравенствами |
|||
−π |
< arctgα < π , |
то полярный угол можно находить по следу- |
||||||
2 |
2 |
|
|
|
|
|
|
|
ющему правилу: |
|
|
|
|
|
|
|
|
|
|
y |
0, если x > 0 |
|
|
|||
|
|
ϕ = arctg |
|
|
+ |
|
. |
(5.3) |
|
|
|
|
|||||
|
|
x |
π , если x < 0 |
|
|
|||
|
|
|
|
|
|
|
|
|
Причем, если x = 0, òî arctg(ϕ ) = π |
ïðè y > 0 |
è arctg(ϕ ) = −π |
||||||
|
|
|
|
|
2 |
|
|
2 |
ïðè |
y < 0. В случае равенства обеих координат нулю, что соответс- |
|||||||
твует нулевому радиус-вектору r = (0,0) = 0, будем считать угол неопределенным. Такой выбор определения угла удобен, например, при решении задач о малых колебаниях вблизи точки с ϕ = 0.
Однако, в других физических приложениях удобнее пользоваться иным способом определения угла, при котором угол ϕ всегда определяется в направлении вращения против часовой стрелки. В этом случае можно определить область значений фун-
62
