Учебник

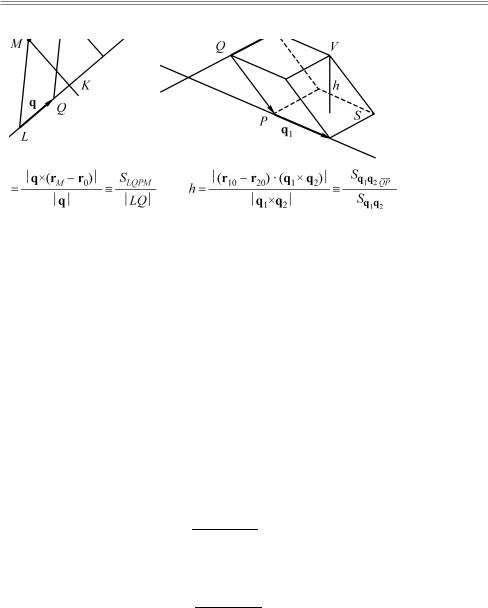
13. Задачи на взаимное расположение точек, прямых и плоскостей

Ðèñ. 13.1. Расстояние от точки до прямой и между скрещивающимися прямыми

Пусть точка K на прямой задана своим параметром:

Отсюда получаем, что

tK = − (r0 −rM ) q . q2

Следовательно, радиус-вектор точки K равен

rK = r0 − (r0 −rM ) q q. q2

Çíàÿ rK , можно задать уравнение перпендикуляра, например, как уравнение прямой, проходящей через две точки.

203

II. Прямые и плоскости. Кривые и поверхности

Кроме того, можно проверить согласованность разных решений. Так, для разности rK −rM мы теперь получаем выражение

rK −rM = r0 −rM − (r0 −rM ) q q = q ×(r0 −rM ) ×q, q2 q2

совпадающее с (13.2.1).

Задача 13.3. Найти расстояние между скрещивающимися прямыми. Построить уравнение общей нормали.

Решение. Эту задачу тоже можно решать в три этапа. Сна- чала найдем расстояние между скрещивающимися прямыми. Потом дадим геометрическое объяснение полученного ответа, а затем получим уравнение прямой — общей нормали к данным прямым.

1. Пусть обе прямые заданы векторными параметрическими

направляющие векторы q1 è q2. Величины u è v являются параметрами для первой и второй прямой соответственно.

В этом случае сразу можно указать вектор N, перпендикулярный обеим прямым:

N = q1 ×q2 .

Этот вектор является направляющим вектором для общего перпендикуляра.

Теперь соединим направленным отрезком любую точку на второй прямой Q с любой точкой на первой прямой P :

QP = rP −rQ = r10 +q1uP −r20 −q2vQ .

Предположим, что вектор KM , соединяющий точку K на второй прямой с точкой M на первой, перпендикулярен обеим

êè Q на прямую KM , а точка M — ортогональной проекцией точки P на прямую KM . Следовательно, отрезок KM åñòü íå

204

13. Задачи на взаимное расположение точек, прямых и плоскостей

что иное, как ортогональная проекция отрезка QP на отрезок KM или на вектор N = q1 q2 :

Длина этого вектора равна расстоянию между скрещивающимися прямыми:

2. Геометрический смысл полученного результата.

Давайте получим выражение (13.3.2) методом, аналогичным приведенному во втором действии задачи 13.2. От произвольной точки Q второй прямой отложим векторы q1, q2 и направленный отрезок QP, где точка P — произвольная точка первой прямой. Теперь построим на этих трех векторах параллелепипед. Высота этого параллелепипеда и будет определять расстояние между данными скрещивающимися прямыми.

Объем этого параллелепипеда равен модулю смешанного произведения этих трех векторов:

V= QP (q1 q2 ) ,

àплощадь основания определяется величиной векторного произведения векторов q1, q2 :

S = q1 q2 .

205

II. Прямые и плоскости. Кривые и поверхности

Следовательно, высота оказывается равной

Это соотношение совпадает с результатом (13.3.2) и объясняет его геометрический смысл.

3. Для полного решения задачи нам надо определить местоположение точек K è M , которые были введены в первом действии. Эти точки являются концами общего перпендикуляра к заданным скрещивающимся прямым. Следовательно, направленный отрезок

KM = r10 +q1u −r20 −q2v

перпендикулярен нормали N = q1 q2 , общей для заданных прямых. Здесь u — значение параметра, соответствующее точке M , à v — точке K. Условие перпендикулярности выразим в виде равенства нулю соответствующих скалярных произведений:

где для удобства введен вектор с = r10 −r20 . После простейших преобразований получаем такую систему уравнений для неизвестных u è v :

Решение этой системы можно записать в виде

= (с q1 )q22 −(с q 2 )(q1 q 2 ) = (с q 2 )(q1 q 2 ) −(с q1 )q22 .

−

206

13. Задачи на взаимное расположение точек, прямых и плоскостей

Здесь величина = q12q22 −(q1q2 )2 может быть записана в виде

= (q1 q2 )2 ,

полученном в задаче 8.5. Выражение для числителя можно пока не упрощать.

Для второго параметра v аналогично получаем:

v = (с q1 )(q1 q 2 ) −(с q 2 )q12 .

Мы получили значения параметров, соответствующие точкам K è M , и следовательно, знаем теперь радиус-векторы этих то- чек и можем построить уравнение общего перпендикуляра как прямой, проходящей через эти точки.

С другой стороны, мы получили еще одно выражение для вектора KM = r10 +q1u −r20 −q2v, которое должно совпадать с ранее полученным (13.3.1).

207

II. Прямые и плоскости. Кривые и поверхности

Убедиться в том, что левую часть этого равенства можно представить в виде правой части можно таким способом. Представим левую часть этого равенства в виде неизвестного вектора X :

X = ρ (q12q22 −(q1q2 )2 )+q1 ((ρ q 2 )(q1 q 2 ) −(ρ q1 )q22 ) − −q2 ((ρ q1 )(q1 q 2 ) −(ρ q 2 )q12 ).

Сначала скалярно умножаем X поочередно на векторы q1 è íà q2 и убеждаемся в том, что эти произведения равны нулю. Значит, вектор X перпендикулярен векторам q1 íà q2 , и следовательно, он параллелен вектору q1 ×q2 и его можно представить в виде

X = λ (q1 q2 ).

Чтобы найти коэффициент λ , умножаем X на векторное произведение (q1 q2 ) и для λ получаем следующее соотношение:

((q1 q2 )ρ)(q12q22 −(q1q2 )2 )= λ (q1 q2 )2 .

Отсюда находим, что

λ = (q1 q2 )ρ.

Следовательно, вектор X равен

X = ((q1 q2 )ρ)(q1 q2 ),

что и следовало доказать.

В качестве дополнительного упражнения можно доказать равенство (13.3.3) путем последовательных прямых преобразований левой части в правую. Дадим небольшую подсказку. Если перенести первое слагаемое в левой части направо, то в правой части окажется двойное векторное произведение некоторых векторов.

208

13. Задачи на взаимное расположение точек, прямых и плоскостей

Задача 13.4. Взаимное расположение прямых на плоскости

èплоскостей в пространстве. Алгебра и геометрия.

Âнашем курсе мы неоднократно отмечали, что аналитическая геометрия предоставляет замечательную возможность представить многие алгебраические теоремы и задачи в наглядном виде. Давайте рассмотрим пример решения системы двух уравнений с двумя неизвестными:

A1x + B1 y = −C1 .A2 x + B2 y = −C2

Решение. В начале предположим, что в правой части этих уравнений не стоят одни нули, то есть хотя бы один из коэффициентов Ci не равен нулю. Такая система уравнений называется неоднородной системой, и алгебраическое решение этой

Это решение единственно, когда знаменатели в этих выражениях не равны нулю. Напомним, что в знаменателе этих выражений стоит так называемый определитель системы уравнений:

= A1B2 − A2 B1.

Если знаменатели равны нулю, а числители не равны нулю, то решение отсутствует. Возможен случай, когда и числители, и знаменатели равняются нулю, то есть выполняется соотношение

A2 : A1 = B2 : B1 = C2 : C1.

209

II. Прямые и плоскости. Кривые и поверхности

Тогда уравнения системы являются по сути одним и тем же уравнением, и система имеет множество решений, в которых неизвестные оказываются зависимыми друг от друга. Связь между переменными определяется любым из уравнений системы

A1x + B1 y = −C1, A2 x + B2 y = −C2 или любым уравнением, полу- ченным из них при умножении на ненулевое число.

Все эти выводы могут быть представлены и на геометрическом языке. Для этого достаточно заметить, что уравнения системы представляют собой уравнения прямых а совместное решение этих уравнений есть ни что иное , как поиск общих точек у этих прямых.

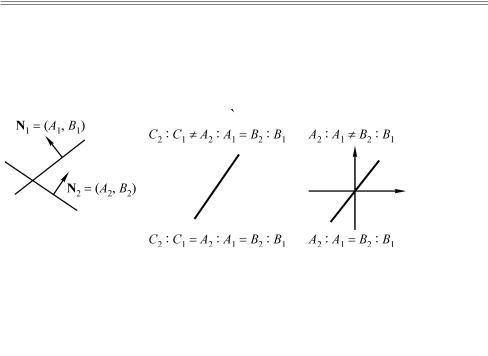
Уравнения в системе представляют собой уравнения прямых, записанные в общем виде. Значит, нам заданы нормали к этим линиям:

N1 = ( A1 , B1 ) è N2 = ( A2 , B2 ).

Равенство нулю определителя системы оказывается эквивалентным параллельности этих векторов:

= A1B2 − A2 B1 = 0 A2 : A1 = B2 : B1 N1 || N2.

Следовательно, если определитель системы не равен нулю, то нормали, а вместе с ними и сами прямые, не параллельны друг другу, а, значит, они имеют единственную точку пересечения.

Если определитель оказывается равным нулю, то это равносильно тому, что прямые оказываются параллельными. Расстояние ρ12 между ними можно определить из нормированного уравнения:

Мы видим, что если для коэффициентов C справедливо такое же отношение, как и для коэффициентов A è B, òî åñòü

C2 : C1 = A2 : A1 = B2 : B1,

то расстояние между параллельными прямыми оказывается равным нулю. Значит, в этом случае прямые совпадают и каждая из них является решением системы. Если это соотношение для

210

13. Задачи на взаимное расположение точек, прямых и плоскостей

коэффициентов C не выполняется, то расстояние между параллельными прямыми не равно нулю, и, следовательно, прямые не имеют общих точек, а система уравнений не имеет решения.

Ðèñ. 13.2. Решение системы уравнений и взаимное расположения двух прямых на плоскости

Мы видим, что между алгебраическим и геометрическим подходами возможна полная эквивалентность. По этой причине рассуждения на языке плоскостей и прямых часто используются при решении задач в алгебре, в частности — систем уравнений большого числа переменных.

Рассмотрим случай, когда правые части обоих уравнений равны нулю — так называемый однородный случай. В этом случае ситуация в некотором смысле обратная. Если определитель системы не равен нулю, то возможно только тривиальное решение: x = 0 è y = 0. Ситуация меняется, когда определитель системы становится равным нулю: A1B2 − A2 B1 = 0. Тогда уравнения системы в силу пропорции A2 : A1 = B2 : B1 опять оказываются одним и тем же уравнением, которое определяет все множество решений системы.

211

II. Прямые и плоскости. Кривые и поверхности

Особенно важны такие решения в физике, когда решается зада- ча о собственных движениях какой-то системы. Так называются движения системы в отсутствие внешних сил, которые играют роль неоднородностей, стоящих в правой части уравнений. Поэтому для решения таких задач нужно приравнять нулю определитель системы уравнений движения этой физической системы.

Задача 13.5. «Отражение» луча от треугольника.

Эта традиционная задача о так называемой трассировке луча света, которая возникает при построении графических изображений в компьютерной графике, где поверхности фигур задаются треугольниками.

В этой задаче нужно определить, имеет ли заданный луч общую точку с заданным в пространстве треугольником, и найти направление отраженного от этой точки луча.

Решение. Предположим, что в пространстве задан луч, исходящий из точки r0 с направляющим вектором q. Тогда уравнение этого луча может быть записано в параметрическом виде:

надлежит. Уравнение этой плоскости запишем в векторном параметрическом виде, выбрав в качестве направляющих векторов любую пару направленных отрезков AB, BC èëè CA :

r = rA +u AB +vAC = rA +u(rB −rA ) + v(rC −rA ). (13.5.2)

Точку пересечения луча (13.5.1) и плоскости (13.5.2) найдем, приравняв соответствующие компоненты в этих векторных уравнениях.

212