Учебник

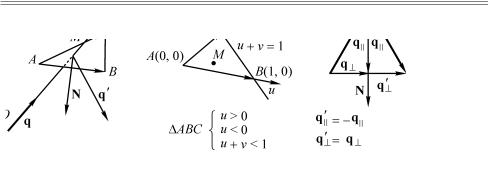
13. Задачи на взаимное расположение точек, прямых и плоскостей

Ðèñ. 13.3. Отражение луча от треугольника. Аффинная система в плоскости треугольника. Законы отражения

Мы получили систему из трех уравнений для трех неизвестных t, u è v.

Предположим, что система имеет единственное решение t0 , u0 è v0 , которые описывают некоторую точку M пересечения луча с треугольником.

Так как заданный луч соответствует положительным значениям параметра t > 0, то величина t0 должна быть положительной:

t0 > 0. (13.5.4)

Осталось проверить, принадлежит ли эта точка треугольнику ABC. Для этого рассмотрим величины u è v как координаты на плоскости ABC в системе отсчета с центром в точке A и осями координат AB è AC. Векторы AB è AC являются при этом базисными векторами. Тогда координаты точек треугольника ABC в этой системе отсчета удовлетворяют следующей системе неравенств: u > 0, v > 0 è u +v <1. В последнем неравенстве мы

Предположим, что точка M оказалась внутри треугольника, и перейдем к следующему действию.

213

14.КРИВЫЕ И ПОВЕРХНОСТИ

ВАНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

14.1.Уравнение кривой и поверхности

Ñпомощью вектора мы можем задать точку в пространстве, если поставим ей в соответствие радиус-вектор. Следовательно,

ñпомощью векторов можно описать и целые множества точек. Например, окружность, которая представляет собой множество точек, лежащих на одинаковом расстоянии R от начала отсчета, может быть задана уравнением

А радиус-векторы любой точки прямой, которая проходит че- рез точку с радиус-вектором r0 и перпендикулярна вектору q, подчиняются соотношению

Такие выражения хороши тем, что они наглядно отражают основные свойства кривой и не зависят от того, задана или нет система координат.

Выражения (14.1) и (14.2) справедливы, если в них подставить радиус-векторы точек соответствующих кривых, то есть они являются уравнениями для радиус-векторов точек этих кривых. Может случиться так, что эти соотношения будут справедливыми для âñåõ точек этих кривых. Более того, может оказаться так, что эти выражения будут справедливы для точек только ýòîé

215

II. Прямые и плоскости. Кривые и поверхности

кривой. Тогда эти соотношения, которые фактически являются уравнениями для радиус-векторов точек кривой можно назвать

уравнением кривой.

Наличие векторов в уравнении кривой позволяет быстро представлять эти уравнения в координатной форме в заданной системе отсчета. Это особенно важно, когда можно подобрать наиболее удобную для решения конкретной задачи систему отсчета.

Кроме того, координатная запись позволяет предложить одну форму записи уравнений для всех кривых. Действительно, и для окружности, и для прямой, соотношения (14.1) и (14.2) можно переписать в виде:

Мы видим, что каждое из соотношений (11.3) и (11.4) записано в следующей форме

Такая запись хороша тем, что с ее помощью можно ввести некоторое обобщенное понятие любых кривых. В таком определении есть некоторые недостатки, например, свойства кривой не так очевидны. Но в то же время есть и преимущества. Так, если кривая задана своим уравнением, то ее свойства можно изучать чисто алгебраическими методами, практически не требующими никаких геометрических построений. А это является одной из целей аналитической геометрии.

Определение уравнения кривой

Уравнение f (x, y) = 0 называется уравнением кривой, если ему удовлетворяют координаты всех точек этой кривой и не удовлетворяют координаты точек, не принадлежащих этой кривой.

Рассмотрим еще несколько примеров, свидетельствующих об особенностях такого способа описания кривой. Предположим,

216

14. Кривые и поверхности в аналитической геометрии

что мы захотели написать уравнение окружности в более общем виде, чем (14.3) x2 + y2 = H , ãäå H — произвольное число. Тогда такое уравнение уже описывает не только окружность, потому что если H = 0, то этому уравнению удовлетворяют координаты только одной точки, а именно — начала отсчета. А если H < 0, то вообще не существует точек, координаты которых удовлетворяли бы этому уравнению.

Похожие примеры можно привести и для прямых. Если выражение y = x можно назвать уравнением прямой, то это же соотношение, возведенное в квадрат, — y2 = x2 , уже будет описывать не только эту прямую, но и прямую y = −x. Таким образом, мы видим, что уравнение f (x, y) = 0 может описывать как кривые, так и множества точек, отличные от кривых, — отдельные точ- ки, несколько кривых. А если вспомнить классический пример с уравнением x − x = 0, то становится понятно, что с помощью уравнений f (x, y) = 0 можно описывать даже части плоскостей.

Чтобы таких трудностей не возникало, достаточно помнить, что выражение f (x, y) = 0 не является определением кривой через координаты ее точек. То есть кривая — это понятие, для нас неопределяемое, так же как и, например, точка. А уравнение кривой — это всего лишь удобная запись, отражающая связь между координатами точек кривой.

Такая же ситуация имеет место в физике, где уравнения являются не определением или объяснением физических законов, а математическим способом их описания.

Приведенный способ f (x, y) = 0 описания кривой с помощью соотношений между числами уравнения кривой, конечно же, не является единственным. Собственно говоря, мы могли записать координаты всех точек кривой в виде таблицы, содержащей абсциссу и соответствующую ей ординату, и получили бы своеобразный, очень громоздкий, табличный способ задания кривой. Этим способом практическим всегда пользуются в компьютерных изображениях для описания кривой в растровой графике, когда изображение разбивается на большое количество элементов, каждый из которых окрашивается только в один цвет.

Еще один способ описания кривой подсказывает нам физика. Мы знаем, что тело, брошенное с некоторой начальной скоростью

217

II. Прямые и плоскости. Кривые и поверхности

V0 под углом α к горизонту, движется в поле тяжести Земли так, что его координаты подчиняются следующим уравнениям:

бодного падения.

Эти соотношения описывают некоторую линию в пространстве, которая называется траекторией тела. При этом для каждой из координат тела есть свое уравнение, в которое не входит другая координата. Основной же величиной, которая определяет изменение координат, является время. То есть время является некоторым параметром, каждому значению которого соответствует некоторая точка на траектории. И изменяя непрерывно значения времени, мы побываем поочередно во всех точках кривой. Таким же образом можно поступить и практически с любой кривой. Достаточно представить, что вдоль кривой движется материальная точка и определить законы изменения каждой из координат по отдельности, введя в качестве параметра какую-нибудь подходящую величину.

Например, при равномерном вращении по окружности с радиусом параметром может быть угол поворота. Тогда координаты вращающегося тела можно будет описывать следующими соот-

Такой способ описания кривой называется параметрическим:

Одним из достоинств параметрического способа задания кривой является то, что он легко обобщается на случай многомерных задач. Например, в трехмерном пространстве параметрическое уравнение кривой записывается так:

218

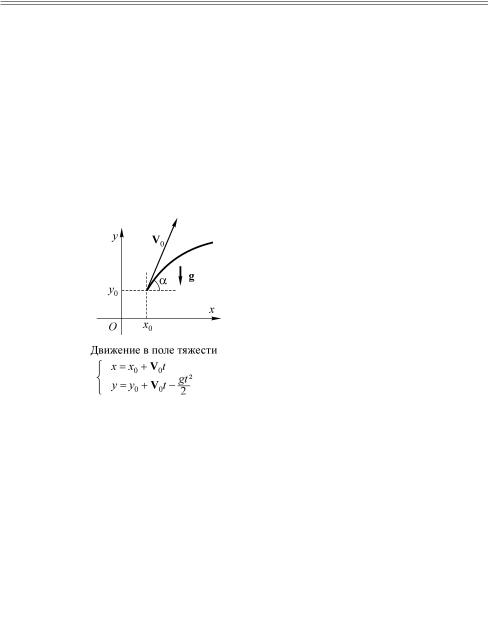
14. Кривые и поверхности в аналитической геометрии

Примером такой кривой служит винтовая кривая, которая задается следующими соотношениями:

Ðèñ. 14.1. Примеры задания кривых с помощью соотношения f (x, y) = 0 (а), с помощью таблицы (б) и с помощью параметрического уравнения (в) {x = x(t); y = y(t)}

219

II. Прямые и плоскости. Кривые и поверхности

Задать же кривую в пространстве с помощью одного уравнения типа f (x, y) = 0, добавляя в нее третью координату, не удается. Дело в том, что уравнение вида

описывает плоскость YOZ, а уравнение x2 + y2 + z2 − R2 = 0 соответствует сфере.

Задать же линию в пространстве, не используя параметра,

Заметьте, что такая же система получается, если исключить параметр из параметрического уравнения кривой в пространстве (14.9). Для этого мы предполагаем, что, например, первое из уравнений (14.9) можно разрешить относительно переменной x, то есть существует функция t = t(x). А затем подставляем эту функцию в оставшиеся два уравнения и получаем систему двух уравнений вида (14.12):

Например, биссектриса угла XOY может быть задана с помощью параметрических уравнений, из которых можно полу- чить уравнение этой же кривой как пересечения горизонтальной плоскости XOY и плоскости, делящей пополам угол между плоскостями XOZ è ZOY.

Аналогичным способом можно показать, что и на плоскости различные уравнения кривой f (x, y) = 0 и параметрическое {x = x(t); y = y(t)} могут быть сведены друг к другу.

220

14. Кривые и поверхности в аналитической геометрии

Давайте вернемся к уравнению поверхности в пространстве f (x, y, z) = 0. Простейшими примерами таких поверхностей являются плоскости. Предположим, что нам известна точка с ра- диус-вектором r0 , принадлежащая этой плоскости, и мы знаем два неколлиненарных вектора q1 è q2 , параллельных этой плоскости. Тогда на плоскости можно ввести собственную двумерную систему координат, выбрав эту точку в качестве начала отсчета, а эти векторы — в качестве базисных. В этом случае радиус-вектор любой точки на этой плоскости может быть представлен в виде r = r0 +uq1 +vq2 , где коэффициенты u è v являются координатами вектора r −r0 в системе отсчета, выбранной на плоскости. Если мы запишем это соотношение в координатном виде, то мы получим, что каждая из координат является функцией двух вели- чин, которые, могут рассматриваться как некоторые параметры:

Оказывается, и многие другие поверхности могут быть записаны в аналогичном параметрическом âèäå:

Примером параметрического описания поверхности служит сфера радиуса R, координаты точек на которой можно задавать с помощью угловых сферических координат:

Нетрудно показать, что после исключения угловых переменных из этих уравнений получаем известное уравнение сферы x2 + y2 + z2 = R2.

221

II. Прямые и плоскости. Кривые и поверхности

14.2. Алгебраические кривые и поверхности

Представьте, что вам задана кривая на плоскости уравнением y = 0. Это прямая, совпадающая с осью абсцисс. Теперь рассмотрим эту же прямую с точки зрения другой системы от- счета, которая повернута относительно исходной на 90 градусов. В новой системе отсчета эта прямая совпадет с осью ординат, и ее уравнение в новых координатах будет иметь вид x1 = 0.

Если новая система сдвинута относительно исходной, например, вниз на величину h, то в этой новой системе отсчета уравнение той же прямой будет иметь вид y2 = −h.

Если же новая система сдвинута относительно исходной на

y =Y0 + x3 sinϕ + y3 cosϕ = 0.

Все эти уравнения объединяют два фактора. С точки зрения геометрии они описывают одно и то же множество точек — прямую. А с точки зрения алгебры все они являются полиномами первого порядка.

Аналогичный пример можно привести и для окружности. Пусть окружность задана в исходной системе отсчета K уравнением x2 + y2 = R2 . Тогда в другой системе отсчета K ′, которая отличается от исходной поворотом и параллельным переносом, уравнение окружности будет иметь вид:

( X0 + x′cosϕ − y′sinϕ )2 +(Y0 + x′sinϕ + y′cosϕ )2 = R2 .

Если раскрыть скобки, то мы опять убедимся, что уравнение окружности является полиномом второго порядка, как и в исходной системе отсчета.

222