Учебник

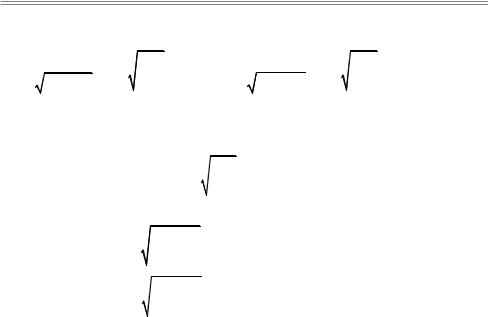
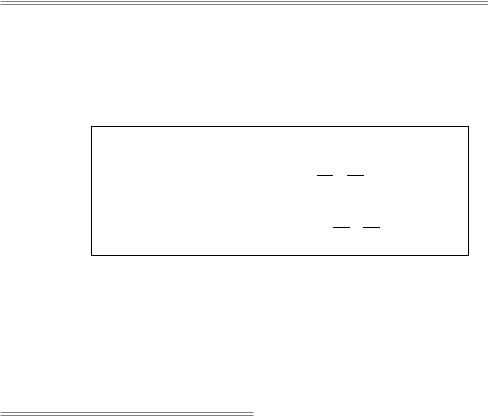
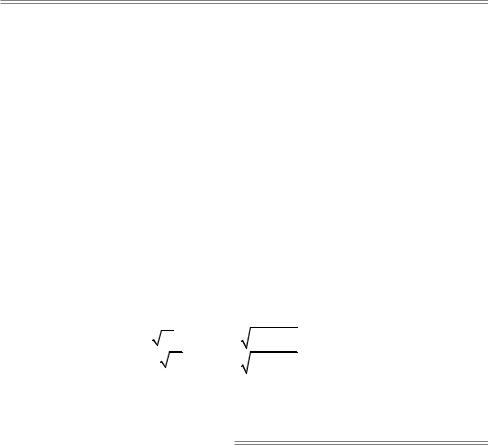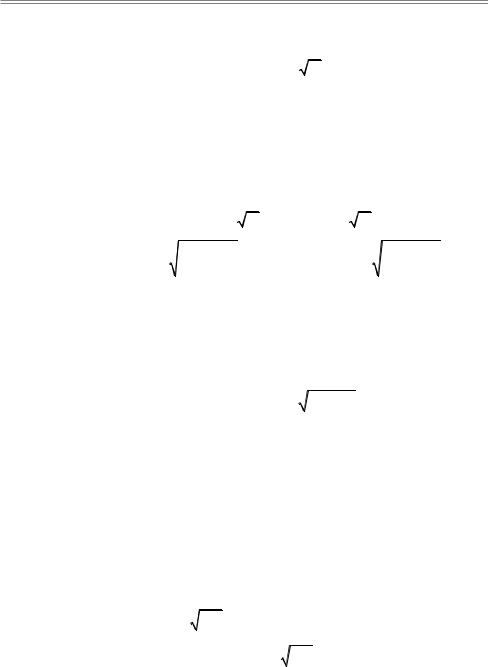21. Определение параметров и построение кривых по общему уравнению

Вершина параболы теперь определяется как пересечение оси параболы (21.50) с исходным общим уравнением параболы:

a11x2 + 2a12 xy + a22 y2 + 2a13 x + 2a23 y + a33 = 0.

Прямой подстановкой (21.50) в это общее уравнение можно убедиться, что из-за равенства нулю второго инварианта I2 = a11a22 −a122 = 0 мы получим не квадратное, а линейное уравнение с одним корнем, определяющим координаты вершины параболы, то есть начала отсчета канонической системы координат.

Задача 21.1. Получите следующее инвариантное выражение для эксцентриситета кривой второго порядка:

21.7. Определение параметров кривой второго порядка

1. Общее уравнение кривой второго порядка

a11x2 + 2a12 xy + a22 y2 + 2a13 x + 2a23 y + a33 = 0.

2. Эллипсы и гипербола

2.1.Координаты центра:

a11 X0 + a12Y0 + a 13 = 0 .a12 X0 + a 22Y0 + a 23 = 0

333

III.Кривые и поверхности второго порядка

2.2.Корни характеристического уравнения:

2.3. Дискриминант:

D= (a11 −a22 )2 + 4a122 = I12 − 4I2 .

2.4.Угол поворота ( S = ±1 ):

2.5. Вещественный и мнимый эллипс:

S = −sign I1.

2.6. Полуоси:

2.7. Гипербола:

S = sign I3.

3. Пересекающиеся прямые (диагонали основного прямоугольника)

(a12 ± −I2 ) (x − X0 ) + a22 ( y −Y0 ) = 0 èëè a11 (x − X0 ) +(a12 ± −I2 ) ( y −Y0 ) = 0.

334

22. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

22.1. Общее уравнение. Поверхности второго порядка

После столь подробного изучения кривых второго порядка мы перейдем к поверхностям второго порядка и рассмотрим вкратце лишь их основные свойства. Исследовать эти поверхности удобно, исходя прямо из их общего уравнения. Это уравнение второго порядка, содержащее пространственные координаты:

Путем поворотов и параллельных переносов в трехмерном пространстве мы можем существенно упростить это уравнение, получив, как и в случае с кривыми, приведенные уравнения.

Для начала совершим три последовательных поворота вокруг осей координат или, другим словами, в координатных плоскостях. Это позволит нам избавиться от всех недиагональных слагаемых в общем уравнении и в итоге получить следующее соотношение:

Теперь возможны различные варианты дальнейших преобразований, связанные с отличием от нуля старших коэффициентов.

Если все старшие коэффициенты не равны нулю, то мы можем совершить параллельный перенос вдоль каждой из осей и избавиться тем самым от линейных слагаемых:

336

22. Поверхности второго порядка

Возможна ситуация, когда лишь два из старших коэффициентов не равны нулю. Тогда одно из линейных слагаемых остается. В этом случае с помощью параллельного переноса уравнение можно привести к виду

И, наконец, возможна ситуация, в которой не равен нулю только один из старших коэффициентов:

Наряду с этими тремя уравнениями возможна и ситуация, когда в уравнении после приведения не окажется одной из переменных, и тогда поверхность окажется цилиндром. В этом случае приведенное уравнение будет иметь такой же вид, как уравнение кривой второго порядка. Значит, цилиндрических поверхностей второго порядка будет девять, в соответствии с количеством кривых второго порядка:

Поверхности второго порядка

I–IX. Цилиндры, соответствующие девяти кривым второго порядка.

Заметьте, что цилиндру соответствует и уравнение (22.5а). Ведь мы всегда можем совершить еще один поворот в плоскости YOZ, так чтобы в новых координатах осталось только одно линейное слагаемое, например

Раз уж мы начали с простейших (вырожденных) поверхностей, то давайте рассмотрим возможность существования конусов. Среди функций (22.3), (22.4) и (22.5) однородной может

337

III. Кривые и поверхности второго порядка

быть только функция (22.3), если в ней свободное слагаемое a44 = 0. В этом случае возможны две ситуации. Если знаки ко-

эффициентов в уравнении a11 x2 + a22 y2 + a33 z2 = 0 различны, то поверхность является обычным (вещественным) конусом с вер-

шиной в начале координат. Если же знаки совпадают у всех трех коэффициентов, то уравнению a11 x2 + a22 y2 + a33 z2 = 0 удовлетворяют координаты только одной точки — начала отсче- та. С другой стороны, такую поверхность можно назвать мнимым конусом. Таким образом, мы получили еще две поверхности второго порядка.

Поверхности второго порядка

X. Вещественный конус: x2 + y2 − z2 = 0. a2 b2 c2

Перейдем к более сложным поверхностям второго порядка. Приведенное уравнение (22.3) содержит только квадраты координат, из чего мы делаем вывод о существовании у этих поверхностей центра симметрии. Знаки же перед старшими коэффициентами могут быть разными. Так, в случае, когда эти знаки совпадают, получаем уравнение, похожее на уравнение эллипса, но содержащее три координаты. Поэтому в этом случае запишем уравнение поверхности в виде, аналогичном каноническому уравнению эллипса:

Здесь опять же возможны две ситуации. Если справа стоит плюс единица, то у уравнения возникает множество решений. Эти решения описывают определенную поверхность, которую называют эллипсоидом. Если же справа стоит минус единица, то вещественных решений у такого уравнения нет, и полученную

338

22. Поверхности второго порядка

поверхность называют мнимым эллипсоидом. Итак, мы получи- ли еще две поверхности второго порядка.

Если знаки у старших коэффициентов в уравнении (22.3) разные, то возможных ситуаций опять будет две. В первом случае только у одного старшего коэффициента знак совпадает со знаком свободного члена, а во втором случае — только у двух. Поэтому уравнение (22.3) можно переписать в таком виде:

Мы получили уравнения еще двух поверхностей — гиперболоидов, названия которых — однополостный и двуполостный — станут ясными после изучения их свойств в соответствующем разделе.

XV. Двуполостный гиперболоид: x2 + y2 − z2 = −1. a2 b2 c2

ев совпадающих и несовпадающих знаков у старших коэффициентов, то есть, это уравнение можно записать в виде

339

III. Кривые и поверхности второго порядка

Поверхности, которые описываются этим уравнением, не имеют центра симметрии и называются параболоидами.

Поверхности второго порядка

XVI. Эллиптический параболоид: x2 + y2 = 2z. a2 b2

XVII. Гиперболический параболоид: x2 − y2 = 2z. a2 b2

Итак, мы перебрали все возможные поверхности второго порядка и для невырожденных поверхностей привели канони- ческие уравнения. Теперь можно, исходя из канонических уравнений, провести исследования этих поверхностей и попытаться наглядно их себе представить.

22.2. Эллипсоиды

Алгебраический анализ этого уравнения показывает, что разрешенные значения координат лежат внутри определенных границ:

−a ≤ x ≤ a

−b ≤ y ≤ b. (22.10)

−c ≤ z ≤ c

340

22. Поверхности второго порядка

Следовательно, эллипсоид заключен внутри некоторого прямоугольного параллелепипеда, который является аналогом основного прямоугольника у эллипса.

Если мы произведем масштабирование координат, то есть «растянем» координаты:

то в новых координатах уравнение эллипсоида будет выглядеть как уравнение сферы: x′2 + y′2 + z′2 =1. Значит, с одной стороны, сфера является частным случаем эллипса, а с другой стороны, эллипсоид можно представить себе как «сжатую» сферу. На рис. 22.1 приведен пример эллипсоида.

Ðèñ. 22.1. Эллипсоид

Если мы построим сечения эллипсоида плоскостями, параллельными координатным плоскостям, то ими окажутся достаточ- но простые кривые, а именно — эллипсы, например:

341

III. Кривые и поверхности второго порядка

По этой причине исследование формы эллипсоида можно было проводить и с помощью сечений.

22.3. Гиперболоиды

Для построения гиперболоидов мы воспользуемся методом вращения кривых. Давайте в плоскости YOZ (x = 0) построим гиперболу:

таком вращении не изменяется, а в исходной кривой эта точка находилась на расстоянии y от этой оси. Потому уравнение поверхности можно получить из уравнения кривой (22.13) заменой переменной y на величину x2 + y2 :

Мы получили так называемый гиперболоид вращения. Если теперь его сжать вдоль оси OX , то мы получим поверхность, уравнение которой имеет вид

то есть однополостный гиперболоид. Такое название станет понятным, если рассмотреть другие, двуполостные, гиперболоиды.

Для этого построим в плоскости YOZ гиперболу, сопряженную (22.13):

342