Учебник

11. Прямые на плоскости

ходящих из этой точки и параллельных этому вектору. Такое множество точек можно называть прямой.

Аналогичным образом, если взять два неколлинеарных вектора и от некоторой точки откладывать отрезки, которые являются линейными комбинациями этих векторов, то множество точек-концов этих отрезков можно называть плоскостью.

Таким образом, с помощью векторов можно вводить понятия прямых, плоскостей и т. д., причем делать это можно в любых пространствах, в которых существуют понятия векторов и точек.

Здесь следует отметить, что такое описание прямых и плоскостей не является, строгим математическим определением, а является скорее, способом их алгебраического описания с помощью векторов.

Вернемся к примеру с прямой линией. Итак, договоримся называть прямой, заданной вектором q и проходящей через заданную точку M0 , множество точек M , которые являются концами направленных отрезков, выходящих из точки M0 и параллельных q :

M0M || q.

Очевидно, что все такие отрезки могут быть представлены в виде

Теперь предположим, что эта прямая задана в каком-то пространстве, например на плоскости или в трехмерном пространстве. В этом пространстве можно выбрать некоторую начальную точку O, и все точки в нем характеризовать соответствующими

173

II. Прямые и плоскости. Кривые и поверхности

Здесь r0 — радиус-точки M0 , через которую проходит данная прямая.

Теперь мы можем предположить, что это уравнение описывает âñå точки этой прямой при изменении величины t îò −∞ äî +∞, причем описывает точки только этой прямой. Тогда выражение (11.2) можно назвать уравнением этой прямой.

Такое уравнение содержит радиус-вектор точки, через которую прямая проходит. Кроме того, в это уравнение входит вектор, которому прямая параллельна, и он называется направляющим вектором. Также в нем содержится величина t, разным зна- чениям которой соответствуют разные точки прямой. Поэтому такое уравнение называется векторное параметрическое уравнение прямой. Основным свойством этого уравнения является то, что его вид не зависит от свойств пространства, в котором оно задано, например оно не зависит от размерности. Это уравнение будет первым из возможных способов описания прямых:

векторное параметрическое 1. rM = r0 +qt — уравнение прямой.

В качестве точки, через которую проходит прямая, можно выбрать, естественно, любую точку прямой, а в качестве направляющего вектора можно выбрать любой вектор, параллельный этой прямой. Предположим, что нам известна еще одна точка этой прямой, например M1. Тогда вектор M0 M1 = r1 −r0 может быть направляющим вектором прямой и уравнение прямой примет вид:

векторное параметрическое

2. rM = r0 +(r1 −r0 )t — уравнение прямой, проходящей через две точки.

Заметим, что найти на прямой радиус-вектор любой точки M1, отличной от точки M0 , можно, если подставить любое ненулевое значение параметра t в векторное параметрическое уравнение (11.2).

174

11. Прямые на плоскости

Другие способы задания прямой связаны с координатным представлением, поэтому они будут рассмотрены отдельно для плоскости и трехмерного пространства.

11.2. Общее уравнение прямой на плоскости

Сначала мы рассмотрим прямую в двумерном пространстве, то есть на плоскости. В этом случае векторное параметрическое уравнение (11.2) записывается в координатном виде следующим образом:

3.x = x0 + qxt — параметрическое уравнение прямой.

y = y0 + qyt

Если задан не направляющий вектор, а две точки, через которые проходит прямая, то параметрическое уравнение в координатном виде примет вид:

Теперь докажем теорему.

Теорема об общем уравнении прямой на плоскости

Общее уравнение прямой на плоскости имеет вид:

Ax + By +C = 0.

Доказательство

В любой из вышеприведенных систем уравнений можно исключить параметр t и получить уравнение, содержащее только координаты точек прямой. Например, из первой системы полу- чим, что

xqy − yqx = x0qy − y 0 qx .

175

II. Прямые и плоскости. Кривые и поверхности

Так как направляющий вектор не равен нулю, то значит что, хотя бы одна из его координат не равна нулю. Следовательно, полученное уравнение является алгебраическим уравнением первого порядка. А так как порядок алгебраической кривой при линейных преобразованиях координат не изменяется (см. теорему в разделе 14), значит, в любой системе отсчета прямая будет описываться уравнением первого порядка. Таким образом, в общем случае уравнение прямой имеет вид:

Только что мы доказали, что прямую можно описать уравнением Ax + By +C = 0, но для того, чтобы утверждать, что уравнение Ax + By +C = 0 является уравнением прямой, нам еще необходимо доказать, что это уравнение описывает только прямые, то есть ничего, кроме прямых.

Рассмотрим случай, когда оба коэффициента A è B не равны нулю. Найдем какую-либо точку с координатами (x0 , y0 ), через которую проходит эта кривая. Координаты этой точки будут удовлетворять уравнению Ax0 + By 0 +C = 0. Вычтем это уравнение из уравнения кривой:

Ax + By +C −( Ax0 + By 0 +C) = A(x − x0 ) + B( y − y 0 ) = 0

и перепишем последнее соотношение в виде:

A(x − x0 ) = −B( y − y 0 ).

Так как левая часть этого равенства не зависит от переменной y, а правая часть не зависит от переменной x, то, значит, оба они могут быть представлены в виде выражения, не содержащего ни x, íè y, то есть в виде некоторого числа t :

A(x − x0 ) = −B( y − y 0 ) = t.

Это число играет роль параметра, определяющего значения обеих переменных.

176

11. Прямые на плоскости

Из последнего соотношения получаем для каждой из переменных:

а это уравнение описывает множество точек, которое мы называем прямыми.

Если хотя бы один из коэффициентов, например A, равен нулю, то общее уравнение приобретает вид By +C = 0, òî åñòü y = −B / C ≡ y0 , а координата x может иметь любые значения. В этом случае уравнение кривой опять можно записать в виде

описывает прямые, и только прямые, по крайней мере, в соответствии с тем определением прямых, которое мы используем в нашем курсе.

Это уравнение позволит нам получить целый ряд различных способов описания прямой на плоскости.

11.3. Другие виды уравнения прямой

Предположим, что нам известна одна точка M0 (x0 , y0 ), через которую проходит прямая, заданная своим общим уравнением Ax + By +C = 0. Значит, координаты этой точки удовлетворяют

177

II. Прямые и плоскости. Кривые и поверхности

этому уравнению: Ax0 + By0 +C = 0. Вычитая эти уравнения друг из друга, получаем следующее соотношение

A(x − x0 ) + B( y − y0 ) = 0,

которое можно записать в виде скалярного произведения двух векторов:

( A, B) (x − x0 , y − y0 ) = 0.

Второй из этих векторов есть не что иное, как разность радиусвекторов (x − x0 , y − y0 ) = r −r0 точек на этой прямой, поэтому он параллелен прямой. Так как скалярное произведение этих векторов равно нулю, то они перпендикулярны между собой. Поэтому первый из этих векторов ( A, B) ≡ N перпендикулярен прямой и называется нормальным вектором (нормалью) к этой прямой. Таким образом, уравнение прямой может быть записано в виде:

6. N(r −r0 ) = 0 — векторное уравнение прямой.

Значит, прямую на плоскости можно представлять, как множество точек ортогональное заданному вектору.

При доказательстве теоремы об общем уравнении прямой мы показали, что направляющий вектор может быть записан в виде (11.4). Если теперь найти скалярное произведение направляющего вектора на нормальный вектор то мы, как и ожидали, получим ноль:

Nq = ( A, B) 1A , − B1 = 0.

Теперь перепишем соотношение (11.5) в следующем виде:

A(x − x0 ) = −B( y − y0 )

и представим полученное равенство в виде пропорции:

178

11. Прямые на плоскости

Мы видим, что в знаменателях дробей оказались возможные координаты направляющего вектора. То есть, существует еще одна запись для уравнения прямой:

7. (x − x0 ) = ( y − y0 ) — каноническое уравнение прямой. qx qy

Каноническое уравнение прямой обычно получается из параметрических уравнений после исключения из них параметра.

Если на прямой заданы две различных точки, то в качестве направляющего вектора можно взять вектор, соединяющий эти две точки. Тогда каноническое уравнение можно представить в виде уравнения прямой, заданной двумя различными точками.

Следующие два уравнения являются вариантами записи общего уравнения, содержащими различные параметры прямой. Например, если коэффициент B не равен нулю, то после деления на этот коэффициент общее уравнение можно переписать в виде y = kx +b. Здесь k — так называемый угловой коэффициент, который равен тангенсу угла между данной прямой и осью абсцисс. По этой причине такая запись уравнения прямой называется уравнением с угловым коэффициентом.

9. y = kx +b — уравнение с угловым коэффициентом.

По всей видимости, этот вид уравнения прямой наиболее знаком читателю, ведь такая зависимость y = y(x) представляет собой так называемую линейную зависимость и является основной при описании прямой в школьном курсе математики.

Если общее уравнение разделить на −C и перенести получившуюся единицу вправо, то мы получим еще одну запись уравнения прямой:

179

II. Прямые и плоскости. Кривые и поверхности

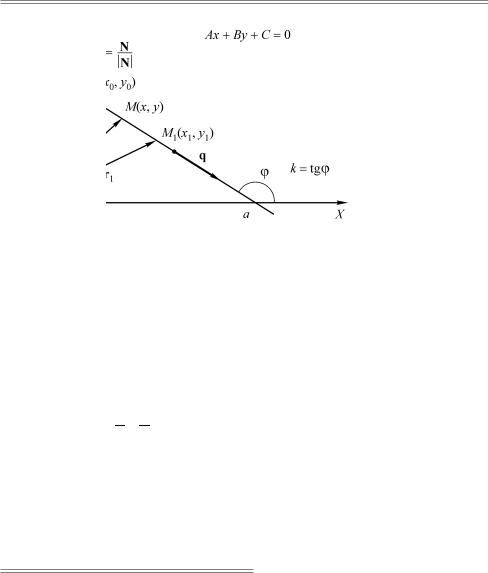
Ðèñ. 11.1. Параметры прямой на плоскости

Величины, которые стоят в знаменателях дробей, определяют величины отрезков, которые данная прямая отсекает на соответствующих осях координат. Действительно, точка пересечения любой прямой, например, с осью ординат имеет абсциссу, равную нулю. Тогда ордината этой точки определяется из этого уравнения и оказывается равной −C / A. Такое уравнение называется уравнением в отрезках.

10. ax + by =1 — уравнение прямой в отрезках.

На рис. 11.1 приведен пример прямой в декартовой системе координат на плоскости с параметрами, которые входят в различные виды уравнения прямой.

11.4. Взаимное расположение точки и прямой. Нормальное уравнение прямой

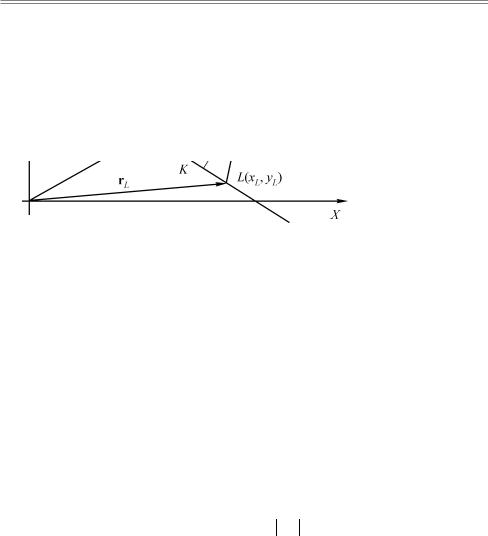
точки M опустим перпендикуляр на прямую и основание этого перпендикуляра отметим как точку K.

180

11. Прямые на плоскости

Тогда относительное положение точки M и заданной прямой можно описывать с помощью направленного отрезка KM . Длина этого отрезка равна расстоянию от точки M до прямой, а его направление указывает, в какой из полуплоскостей лежит точка M . Åñëè KM ↑↑ N, то точка M лежит в той полуплоскости, в которую направлен вектор нормали N = ( A, B), и наоборот.

Ðèñ. 11.2. Нормальное уравнение прямой

Так как вектор KM параллелен M1(x1, y1 ), то его можно представить в следующем виде:

KM = ρM n.

Здесь величина ρM фактически является координатой òî÷- êè M на прямой KM с базисом {n} и началом отсчета в точке K. Значит, абсолютная величина ρM определяет расстояние от M äî K, à çíàê ρM указывает на то, с какой стороны от прямой лежит эта точка. Найти ρM можно из вышеприведенного уравнения, если умножить его на вектор n :

ρM = n KM .

Величину ρM , которую можно назвать отклонением точки от прямой, оказывается, можно находить с помощью общего уравнения прямой.

181

II. Прямые и плоскости. Кривые и поверхности

Давайте возьмем произвольную точку на прямой, например L, и найдем скалярное произведение вектора LM на единичный вектор нормали:

n LM = n (LK + KM ) = n KM = ρM ,

òàê êàê n LK = 0. С другой стороны —

n LM = n (rM −rL ) = n rM −n rL .

Следовательно:

ρM = n rM −n rL .

Скалярное произведение n rL распишем через координаты:

При последнем преобразовании мы использовали тот факт, что точка L лежит на заданной прямой, а значит, ее координаты подчиняются общему уравнению прямой Ax + By +C = 0. Теперь для величины ρM получаем

Из этого соотношения следует, что для определения величины ρM достаточно подставить координаты точки в уравнение прямой и разделить полученный результат на длину вектора нормали.

Это соотношение оказалось настолько удобным при практи- ческих применениях, что для его использования была введена еще одна форма записи уравнения прямой.

182