Учебник

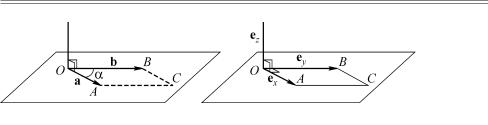
7. Векторное произведение векторов

Ðèñ. 7.1. Векторное произведение векторов: à) определение векторного произведения c =a ×b; á) векторное произведение ортов декартового базиса ex ×ey = ez

В последнем равенстве можно убедиться, например, следующим образом. Так как векторы ex è ey перпендикулярны друг другу, то параллелограмм построенный на них, как на сторонах является квадратом. А так как их длины равны единице, то площадь этого квадрата равна единице. Следовательно, вектор ex ×ey равен по длине единице. Кроме того, по определению векторного произведения этот вектор направлен вверх и перпендикулярен как ex , òàê è ey . Таким образом, вектор ex ×ey по направлению и вели- чине совпадает с вектором ez , òî åñòü ex ×ey = ez .

Для векторного произведения в различных приложениях иногда используют другую запись:

c = a ×b =[a,b].

Аналогично и для скалярного произведения также часто используется запись с помощью скобок:

c = a b = (a,b).

Необычной особенностью векторного произведения является то, что результирующий вектор отличается от множителей своей математической природой. Давайте разберемся, с величиной этого вектора. Пусть в качестве множителей взяты векторы, соответствующие какой-нибудь физической величине, например, перемещению. Тогда длина этих векторов будет иметь определенную размерность, например, сантиметры. Их векторное произведение

103

I. Векторная алгебра

по своей сути будет площадью параллелограмма, построенного на векторах-сомножителях. Поэтому его величина будет иметь совсем другую размерность. В нашем случае — квадратные сантиметры. Поэтому представить этот вектор как обобщение какого-то перемещения не удастся. Таким образом, результат векторного произведения не вписывается в наше определение вектора как обобщения перемещений. Однако при этом мы называем эту величину вектором, да и само название этого произведения — «векторное» — говорит о том, что результатом его является вектор.

Разобраться в этой проблеме мы сможем в разделе, посвященном преобразованию координат, где дадим еще одно определение вектора.

7.3. Свойства векторного произведения

Изучим свойства векторного произведения, которые помогут нам использовать его в дальнейшем при решении самых разнообразных задач. К самым необычным (или непривычным) свойствам векторного произведения относится его антикоммутативность. Мы привыкли, что при сложении или при умножении двух чисел от перемены мест слагаемых или множителей результат не меняется. Векторное произведение является фактически первым примером произведения в курсе математики, в котором результат зависит от порядка множителей:

Убедиться в справедливости этого соотношения можно прямо из определения векторного произведения. Согласно определению 17 а вектор a ×b будет иметь ту же длину a ×b = absin( ab), что и вектор b ×a : длина b ×a = absin( ab) = a ×b . Согласно определению 17 б, векторы a ×b è b ×a будут параллельны друг другу: a ×b || b ×a. А в соответствии с определением 17 в эти векторы должны быть направлены в разные стороны от плоскости, образованной векторами a è b, и следовательно, a ×b ↑↓b ×a.

104

7. Векторное произведение векторов

Из равенства длин и противоположности направлений векторов a ×b è b ×a следует соотношение (7.5).

Второе свойство, которое следует прямо из определения, позволяет использовать векторное произведение для проверки параллельности векторов:

òî ab = 0 (èëè ab =π), а значит sin( ab) = 0, и вместе с ним a ×b = 0 .

Следующее свойство векторного произведения также следует прямо из определения:

Величина a ×b равна площади параллелограмма, построенного на векторах a è b, как на сторонах:

Действительно, давайте от некоторой точки O отложим направленные отрезки, соответствующие векторам a è b : OA = a

Оно может быть доказано прямо из определения, если учесть, что в случае положительного числа λ умножение на него одного из сомножителей не меняет направления результирующего вектора, а только увеличивает его длину в λ раз. Это же происходит и при умножении на число λ и самого векторного произведения, а значит, соотношение (7.8) справедливо. Для отрицательных

105

I. Векторная алгебра

чисел λ можно воспользоваться антикоммутативностью векторного произведения, поменять местами векторы в (7.8) и свести доказательство к предыдущему, в котором теперь в качестве множителя будет фигурировать положительное число λ .

Распределительный закон для векторного произведения векторов выглядит следующим образом:

Этот закон также может быть доказан прямо из определения векторного произведения, однако, существует более лаконичное доказательство, которое мы приведем в следующем разделе, когда изучим свойства смешанного произведения векторов.

Перечислим свойства векторного произведения.

Основные свойства векторного произведения

1. Антикоммутативность (переместительное свойство)

a ×b = −b ×a.

2. Ассоциативность (сочетательное свойство)

(λa) ×b = λ (a ×b).

3. Дистрибутивность (распределительное свойство)

(a1 +a2 ) ×b = a1 ×b +a2 ×b.

4. Параллельность векторов и векторное произведение

a ×b = 0 a || b.

5. Площадь параллелограмма и модуль векторного произведения

a ×b = Sa,b .

106

7. Векторное произведение векторов

7.4. Векторное произведение в декартовом базисе. Тензор Леви-Чивита

Определение векторного произведения дано таким образом, что оно не зависит от того, какие координаты у векторов, то есть не зависит от того, в какой системе координат мы работаем. Этим мы лишний раз подчеркиваем, что, как и у скалярного произведения, результат векторного произведения не зависит от выбора системы координат и существует, даже если система координат вообще не выбрана. Однако, как и в случае со скалярным произведением, в конкретной системе координат, когда у векторов есть определенные координаты, можно определять координаты результирующего вектора по довольно простым формулам.

Возьмем два вектора a = (a1 , a2 , a 3 ) = a1e1 + a2e2 + a3e3 = ∑ii==13 aiei è b = (b1,b2 ,b3 ) = b1e1 +b2e2 +b3e3 = ∑ii==13 biei , и построим их век-

торное произведение:

Пользуясь распределительным законом для векторного произведения, раскрываем скобки в соотношении (7.10) и получаем сумму девяти слагаемых:

a ×b = a1b1e1 ×e1 + a1b2 e1 ×e2 + a1b3e1 ×e3 +

+a2b2e1 ×e1 + a2b2e2 ×e2 + a2b3e2 ×e3 +

+a3b1e3 ×e1 + a3b2e3 ×e2 + a3b3e3 ×e3.

Таким образом, исходное выражение свелось к сумме слагаемых, каждое из которых содержит векторное произведение ортов. Осталось вычислить все возможные произведения ортов, тем более, что мы в качестве примера векторного произведения уже показывали (см. рис. 7.1), что ex ×ey = ez . Таким же образом можно вычислить и остальные произведения:

107

I. Векторная алгебра

Эти соотношения позволяют существенно упростить исходное выражение для произведения a b, которое после приведения подобных слагаемых приобретает такой вид:

К сожалению, эти соотношения достаточно громоздки и неудобны для запоминания. Поэтому существует несколько способов и правил, которые позволяют запомнить выражения для компонентов векторного произведения.

В принципе можно запомнить наизусть все девять произведений (7.11) ортов друг на друга. Но можно поступить и по аналогии с девятью скалярными произведениями ортов, для которых был введен специальный символ (символ Кронекера), позволивший компактно записать все эти произведения: ei e j =δ ij . Здесь мы поступим похожим образом. Результатом векторного произведения двух ортов ei ×e j является вектор этого же пространства, поэтому он может быть разложен по базису этого пространства (e1, e2 ,e3 ) с некоторыми коэффициентами ak (i, j), которые являются функциями индексов i, j :

k =3

ei ×e j = a1 (i, j)e1 + a3 (i, j)e3 + a2 (i, j)e2 = ∑ak (i, j)ek . (7.13)

k =1

Сравнивая это соотношение с результатами (7.11), получаем явные выражения для коэффициентов ak (i, j), например: a3 (1, 2) =1, a3 (2,1) = −1, à a3 (2, 2) = 0 и т. д. Для компактной записи всех зна-

108

7. Векторное произведение векторов

чений коэффициентов ak (i, j) используется специальный символ ak (i, j) = εijk , определенный следующим образом:

+1, если (ijk) = (123),(231),(312)

ε = −1, если (ijk) = (132),(213),(321).

ijk (7.14)

0 в остальныхслучаях

Этот символ имеет собственное название — единичный, полностью антисимметричный тензор Леви-Чивита. Из определения тензора Леви-Чивита видно, что его компонент равен единице, если последовательность индексов (ijk) у этого компонента является циклической перестановкой начальной последовательности (123). Под циклической (круговой) перестановкой понимается перестановка по кругу, то есть индекс 1 переходит в индекс 2, 2 в 3, а 3 в 1. Если у компонента последовательность индексов (ijk) получается из начальной последовательности обычной перестановкой (то есть переменой мест) двух индексов, например 1 и 2 меняются местами, а индекс 3 остается на месте, то такой компонент равен −1. Если же среди индексов у компонента тензора Леви- Чивита есть одинаковые индексы, то такой компонент равен нулю.

Для нас этот тензор важен, потому что с его помощью мы можем представить векторное произведение ортов в декартовом базисе:

k=1

и следовательно, и векторное произведение двух произвольных векторов:

Другими словами, k -ая координата векторного произведения векторов равна

109

I. Векторная алгебра

Это соотношение фактически является первым способом определения компонента вектора, который является результатом векторного произведения векторов.

Исходя из (7.17) и определения (7.14) тензора Леви-Чивита, выпишем в явном виде каждый из компонентов векторного произведения:

(a ×b)1 = a2b3 − a3b2 ,

Мы видим, что, как и следовало ожидать, координаты вектора a ×b совпадают с приведенными в соотношении (7.12).

Если теперь мы перейдем к обычным, буквенным, обозначе- ниям декартовых координат, то из соотношения (7.18) получаем следующее соотношение для координат вектора, который является векторным произведением двух векторов:

Эти соотношения позволяют «сочинить» еще одно правило для запоминания координат векторного произведения.

Если мы хотим найти определенный компонент векторного произведения, то после знака равенства пишем обозначения векторов в том же порядке, что и в векторном произведении:

(a ×b)x = a b.

110

7. Векторное произведение векторов

Затем записываем индексы у множителей так, чтобы они составляли циклическую последовательность ( xyz, yzx èëè zxy):

(a ×b)x = aybz .

Далее ставим знак минус и опять пишем обозначения векторов, но индексы меняем местами:

(a ×b)x = aybz −az by .

Аналогично поступаем и с другими компонентами, не забывая циклически переставлять индексы.

7.5. Векторное произведение в декартовом базисе. Двумерные и трехмерные определители

Давайте еще раз выпишем соотношения (7.12):

a ×b = (a2b3 − a3b2 )e1 +(a3b1 − a1b3 )e2 +(a1b2 − a2b1 )e3.

Как мы только что отмечали, компоненты векторного произведения имеют одинаковую форму — они представляют собой разность соответствующих произведений. Для такой формы записи в математике существует специальное обозначение, в котором сами знаки действий — умножения и вычитания — отсутствуют.

Выражение справа называется определителем, а так как в нем содержатся две строки и два столбца, то определитель в (7.21) называется определителем второго порядка. В этом курсе мы будем рассматривать определители лишь как более компактную запись определенных алгебраических выражений, которая поможет нам, при вычислении векторных произведений. Так, на-

111

I. Векторная алгебра

31

46 = 3 6 −1 4 =18 − 4 =14. При последующем изучении физи-

ки и математики станет понятно, что определители имеют глубокий физический и математический смысл.

Используя понятие определителя, мы можем записать выражение для векторного произведения следующим образом:

Понятие двумерного определителя (7.21) сразу помогло однообразно записать все компоненты векторного произведения и представить в алгебраической форме то правило, которое мы составили в конце предыдущего подраздела. Однако математики не остановились на этом. Оказывается, запись векторного произведения может быть еще более упрощена, если использовать понятие определителей третьего порядка. Эти величины представляют собой сумму тройных произведений и записываются следующим образом:

a1 a2 a3

b1 b2 b3 = a1b2c3 + a2b3c1 + a3b1c2 − a1b3c2 − a2b3c1 − a3b1c2 . (7.23) c1 c2 c3

Приведя подобные слагаемые, замечаем, что выражение (7.23) может быть записано в следующем виде:

112