Учебник

2. Понятие вектора. Операции над векторами

ки равны между собой, они определяют один и тот же вектор. То есть, вектор a может быть записан в следующем виде: a ≡{Ai Bi}, åñëè AB = Ai Bi . Связь вектора с определяющим его направленным отрезком мы будем записывать в упрощенном виде:

Такая запись обозначает, что вектор a состоит из направленных отрезков, равных AB. В то же время, мы будем часто применять и противоположную запись:

Это равенство обозначает, что направленный отрезок AB — это отложенный от точки A отрезок, принадлежащий вектору a как множеству направленных отрезков.

Так как нулевые направленные отрезки могут быть объединены в одно множество равных между собой нулевых направленных отрезков, то они тоже составляют некоторый вектор. Такой вектор называется нулевым. Он обозначается следующим образом:

Так как вектор состоит из равных направленных отрезков, то свойства, которые одинаковы у этих отрезков, могут быть перенесены на вектор и названы свойствами этого вектора. К таким свойствам относятся равенство направленных отрезков, их длина и направление.

Ðèñ. 2.1. Определение вектора

23

I. Векторная алгебра

2.2. Равенство векторов

Мы ввели новое понятие — вектор, и теперь изучим, какими свойствами обладают эти объекты, как их можно между собой сравнивать и какие операции над ними можно производить.

Так как вектор является множеством, вполне логично сравнивать векторы между собой как множества — поэлементно. То есть называть равными такие векторы, у которых равны определяющие их направленные отрезки. Очевидно, что для этого достаточно сравнить хотя бы один из направленных отрезков одного вектора с каким-нибудь отрезком другого вектора. Если эти отрезки окажутся равными, то, согласно определению вектора, каждый из направленных отрезков одного вектора будет совпадать с любым направленным отрезком другого вектора. Тогда такие множества будут эквивалентными, а эти векторы можно назвать равными между собой. Дадим определение равенства векторов.

Определение 3

Векторы называются равными, если равны соответствующие им направленные отрезки.

Пусть a ≡{AC} è b ≡{BD}, тогда a = b AC = BD.

2.3. Длина вектора

Одним из свойств, общим для всех направленных отрезков одного вектора, является их длина. Поэтому перенесение этого свойства на все множество выглядит вполне закономерным. В этом случае мы можем, например, вместо фразы «Этот вектор состоит из направленных отрезков длиной 5 см» сказать: «Этот вектор имеет длину 5 см». Длину вектора будем обозначать таким же значком, как и длину направленных отрезков.

24

2. Понятие вектора. Операции над векторами

Определение 4

Длиной вектора называется длина направленного отрезка, определяющего этот вектор.

a ≡ AC , åñëè a ≡{AC}.

Теперь, когда мы обобщили для векторов такое свойство направленных отрезков как длина, можно обобщить на векторы

èоперации с направленными отрезками.

2.4.Сумма векторов

Несмотря на то, что вектор является множеством, в качестве суммы векторов берется не объединение множеств, соответствующих этим векторам, а обобщение суммы направленных отрезков этих векторов. Для начала нужно доказать, что при сложении равных отрезков получаются одинаковые результирующие отрезки. А затем полученные равные направленные отрезки объединяются в некий вектор, который и называют суммой исходных векторов.

можно будет определить как сумму векторов a è b. Теперь осталось только убедиться, что A1C1 = A2C2 .

Теорема 1

Суммы равных направленных отрезков равны между собой.

Пусть A1B1 = A2 B2 è B1C1 = B2C2 ,

тогда A1B1 + B1C1 = A2 B2 + B2C2 .

25

I. Векторная алгебра

Доказательство

Согласно свойству 1:

Из этих соотношений имеем:

Используя еще раз свойство 1, получаем:

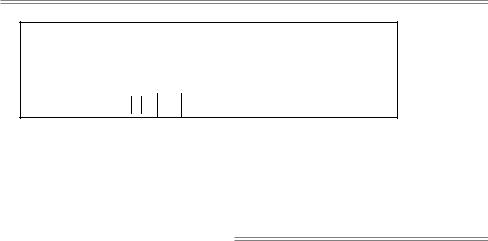
Ðèñ. 2.2. К теореме 1

Таким образом, суммы равных направленных отрезков равны между собой, поэтому вполне могут быть объединены в вектор. Такой вектор называется суммой исходных векторов.

Определение 5

Суммой векторов называется вектор, составленный из сумм направленных отрезков, соответствующих исходным векторам:

a = b +c a = AC, b = AB, c = BC è AC = AB + BC.

26

2. Понятие вектора. Операции над векторами

2.5. Умножение вектора на число

Обобщим для векторов операцию умножения на число направленных отрезков.

Определение 6

Произведением вектора на число называется вектор, составленный из произведений на это число направленных отрезков, соответствующих исходному вектору:

a = λ b a = AC, b = AB, è AC = λ AB.

Чтобы убедиться в возможности такого определения, необходимо доказать, что в результате произведения любого из направленных отрезков исходного вектора будут получены равные между собой направленные отрезки. Только в этом случае их можно будет объединить в вектор. Для этого достаточно доказать теорему, аналогичную теореме 1.

Теорема 2

Произведения равных направленных отрезков на одно и тоже число равны между собой:

Пусть A1B1 = A2 B2 , тогда λ A1B1 = λ A2 B2.

Доказательство

Рассмотрим только частный случай произведения на положительное число. Согласно определению произведения направленного отрезка на число имеем:

27

I. Векторная алгебра

Из соотношений (Т 2.1) и (Т 2.2) и определения равенства направленных отрезков получаем:

A1C1 = A2C2 è A1C1 ↑↑ A2C2 A1C1 = A2C2 . (Ò 2.3)

Аналогично проводится доказательство и для случая λ < 0. ■

2.6. Направление вектора. Орт

Равные направленные отрезки, формирующие один вектор, кроме длины совпадают еще и по направлению. Поэтому направление, наряду с длиной, также может быть отличительной характеристикой вектора как множества направленных отрезков.

На векторы можно перенести такие свойства направленных отрезков как параллельность, сонаправленность и противоположная направленность. При этом для обозначения этих свойств использовать те же обозначения, например:

a ≡{AC} è b ≡{BD}, тогда a ↑↓b AC ↑↓ BD. (2.5)

Если не интересоваться длиной вектора, то для задания направления вектора можно использовать сонаправленный с ним вектор единичной длины. Значение таких векторов очень велико как в самой геометрии, так и в ее приложениях. Поэтому такие векторы

28

2. Понятие вектора. Операции над векторами

получили отдельное название и обозначение. Вектор, сонаправленный данному вектору a и имеющий единичную длину, обознача- ется ea , называется îðò и определяется следующим образом:

Естественно, для нулевых векторов, длина которых равна нулю, орты не определены.

Согласно определению, орты имеют единичную длину ea =1 и с помощью своего орта любой вектор может быть записан в следующем виде:

2.7. Задача на применение понятия орта

Понятие орта является одним из основных понятий в аналитической геометрии и векторной алгебре. При этом введение ортов помогает решать большое количество практических задач. Рассмотрим один из таких примеров.

Задача 2.1. Построить вектор c , направленный по биссектрисе угла, образованного двумя заданными векторами a è b.

Решение. Для решения этой задачи достаточно использовать правило параллелограмма, вспомнив, что диагональ в параллелограмме является биссектрисой, если параллелограмм является ромбом, то есть все его стороны равны. Поэтому достаточно от векторов a è b перейти к векторам a′ è b′, которые направлены также как a è b, но имеют одинаковые длины a′ = b′ . В качестве векторов a′ è b′ можно взять орты векторов a è b : a′ = ea è b′ = eb . Тогда искомое выражение для вектора c будет выглядеть следующим образом:

c = aa + bb .

29

I. Векторная алгебра

Безусловно, можно предложить и другие решения этой задачи, например:

2.8. Свойства линейных операций над векторами

Теперь мы можем привести свойства векторов по отношению к операции сложения векторов и умножения вектора на число. Некоторые из этих свойств можно доказать, пользуясь приведенным выше определением векторов.

В то же время, при построении более общей теории (в векторной алгебре) эти свойства можно рассматривать как набор аксиом, задающих свойства векторов как некоторой группы объектов, которые можно складывать между собой и умножать на числа.

Свойства линейных операций над векторами

1. Коммутативность сложения (переместительное свойство)

2. Ассоциативность сложения (сочетательное свойство)

30

2.Понятие вектора. Операции над векторами

6.Дистрибутивность при умножении суммы

векторов на числа

7. Ассоциативность умножения на числа

λ (μa) = (λμ)a. (2.14)

Свойства 1, 2, 5, 6, 7 могут быть доказаны после перехода к направленным отрезкам с использованием теорем 1 и 2. Свойства 3 и 4 обсуждались для направленных отрезков (раздел 1) и для векторов могут рассматриваться как постулаты.

Наиболее интересным, по-видимому, является доказательство ассоциативности сложения векторов, которое мы здесь рассмотрим.

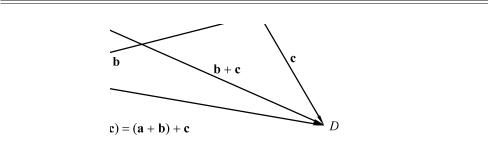
Доказательство ассоциативности сложения векторов

Возьмем три вектора a, b, c и от заданной точки A отложим поочередно направленные отрезки, соответствующие этим векторам:

Введем направленные отрезки

AC = AB + BC = a +b è BD = BC +CD = b +c.

a +(b +c) = (a +b) +c. ■ (Àññ 3)

31

I. Векторная алгебра

Ðèñ. 2.3. Сочетательное свойство сложения векторов