Учебник

14.Кривые и поверхности в аналитической геометрии

Âто же время к линейчатым относятся поверхности, не похожие ни на конусы, ни на цилиндры. Эти поверхности — однополостный гиперболоид и гиперболический параболоид — выглядят достаточно необычно, но анализ этих поверхностей показывает, что их тоже можно получить движением прямой.

Мы исследуем эти кривые в разделе, посвященном поверхностям второго порядка. Так как в этом разделе мы только что изучали конусы, то закономерно возникает такой вопрос. А не является ли гиперболический параболоид конусом с вершиной

âточке O (см. рис. 14.4) и направляющей параболы?

14.5.Поверхности, составленные из окружностей.

Поверхности вращения

Представим, что на плоскости XOY задана окружность с центром в начале отсчета и радиусом R. Нам хорошо знакомы уравнения такой окружности в декартовой системе:

x2 + y2 = R2

и в полярной:

r(x, y) = x2 + y2 = R.

Теперь давайте перемещать эту окружность вертикально вверх или вниз так, чтобы ее плоскость всегда была параллельна плоскости XOY , а центр всегда находился над центром исходной окружности. При таком движении окружность «заметет» поверхность, которая является цилиндром. Уравнение этого цилиндра как поверхности в пространстве будет иметь такой же вид, как и уравнение исходной окружности на плоскости:

233

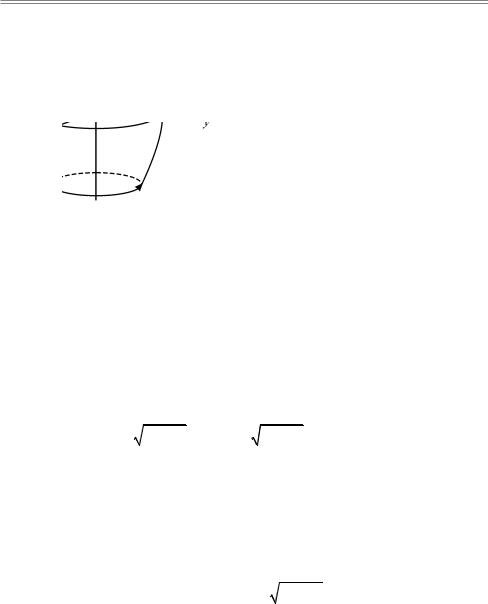
II. Прямые и плоскости. Кривые и поверхности

Представим, что мы двигаем исходную окружность, изменяя ее радиус в зависимости от высоты, то есть предположим, что радиус перемещаемой окружности меняется как некоторая функция z :

Уравнение такой поверхности можно получить, сравнивая формулы (14.23) и (14.22):

r(z) = r(x, y) = x2 + y2 èëè f (r, z) = f ( x2 + y2 , z) = 0. (14.24)

Главной особенностью такой записи является то, что переменные x è y входят в уравнение поверхности в виде комбинации

x2 + y2 = r2 .

Такие поверхности называются поверхностями вращения.

Поверхность вращения — это поверхность, образованная кривой в пространстве при ее вращении вокруг заданной оси. Если осью вращения является ось OZ, то уравнение поверхности вращения можно записать

ââèäå: f (x2 + y2 , z) = 0.

Âсправедливости последнего утверждения можно убедиться

èтаким способом. Предположим, что в плоскости YOZ задана некоторая кривая уравнением

предположим, что некоторая точка M0 (0, y0 , z0 ), которая лежала на исходной кривой, переходит в точку M (x, y, z). Ïðè âðà-

234

14. Кривые и поверхности в аналитической геометрии

щении вокруг оси OZ естественно, не изменяется координата

Ðèñ. 14.5. Пример поверхности вращения

В то же время, так как вращение происходит по окружности, то расстояние между вращающейся точкой и осью вращения не изменяется. Значит

Напомним, что точка M0 (0, y0 , z0 ) лежит на исходной кривой, следовательно, ее координаты удовлетворяют уравнению (14.25):

переходит при вращении, получаем уравнение, которому подчи- няются координаты всех точек поверхности вращения:

Пример поверхности вращения приведен на рис. 14.5, а наглядно представить себе формирование поверхности вращения можно, наблюдая за созданием посуды на гончарном круге.

235

15. ПАРАБОЛА

15.1. Определение и каноническое уравнение параболы

В третьей части учебника мы изучим кривые и поверхности второго порядка и начнем с параболы — кривой, которая всем знакома и описывается квадратичной зависимостью.

Выберем декартову систему отсчета и построим в ней параболу, уравнение которой имеет вид:

Если мы теперь введем другую систему отсчета, которая отли- чается от исходной, например, заменой осей x → y1, à y → x1, то в новой системе отсчета уравнение этой же параболы будет иметь совсем другой вид: x1 = y12 .

Еще заметнее изменится уравнение параболы, если новая система отсчета получена из исходной параллельным переносом на

А если новая система отсчета получена поворотом исходной на угол ϕ , то в новой системе уравнение параболы будет совсем не похоже на исходное:

238

15. Парабола

В этом уравнении параболы уже есть и вторые, и первые степени всех координат — абсцисс и ординат.

Несмотря на такие изменения своего уравнения, сама парабола, как кривая или геометрическое место точек, не изменилась. Значит, вполне вероятно, что параболу можно (или даже нужно) задавать не как график функции (15.1), а как множество точек с определенными свойствами. Дадим одно из возможных геометри- ческих определений параболы:

Парабола — это множество точек, для которых расстояние до заданной точки (фокуса) совпадает с расстоянием до заданной прямой (директрисы).

Найдем уравнение параболы, исходя из данного определения. Для этого выберем наиболее удобную систему отсчета следующим образом.

Проведем прямую, перпендикулярную директрисе и проходящую через фокус параболы. Эту прямую выберем в качестве оси абсцисс. Теперь предположим, что фокус не совпадает с директрисой, и выберем середину отрезка между фокусом и директрисой в качестве начала координат. Осью ординат выберем прямую, проходящую через начало отсчета, и параллельную директрисе.

Ðèñ. 15.1. Определение параболы. Каноническая система отсчета параболы

239

III. Кривые и поверхности второго порядка

Такая система отсчета называется канонической системой от- счета для параболы. Если договориться, что ось абсцисс направлена от директрисы к фокусу, а ось ординат направлена так, что система отсчета является правой, то директриса и не лежащий на ней фокус однозначно определяют каноническую систему отсчета параболы.

Пусть теперь некая точка M с координатами M (x, y) принадлежит параболе. Тогда согласно определению параболы, расстояние от точки M до фокуса равно расстоянию от точки M до директрисы:

Здесь точка D является основанием перпендикуляра, опущенного из точки M на директрису.

Теперь перепишем уравнение (15.1) в координатном виде, используя выражения для расстояния между двумя точками через их координаты:

Мы получили так называемое каноническое уравнение параболы. С помощью этого уравнения можно исследовать свойства параболы.

15.2. Свойства параболы

Первое свойство, которое следует из канонического уравнения параболы, определяет значения переменной x у параболы. Так как в уравнении слева стоит величина y2 , которая всегда поло-

240

15. Парабола

жительна, то, следовательно, переменная x принимает только положительные значения. Это значит, что парабола лежит в правой полуплоскости канонической системы координат.

Более того, если в каноническом уравнении параболы заменить величину y на противоположную, то уравнение не изменит свой вид. Это значит, что ось абсцисс является осью симметрии параболы, поэтому она называется осью параболы. Пересечением оси параболы с самой параболой является точка, которая называется вершиной параболы. Вершина параболы совпадает с началом координат канонической системы отсчета.

Проведем теперь через фокус отрезок, который перпендикулярен оси параболы и концы которого лежат на параболе, — так называемую фокальную хорду. С помощью канонического уравнения можно определить характерные размеры этой хорды, в частности — длину отрезка FN , являющегося половиной фокальной хорды. Длина этого отрезка называется фокальным параметром параболы, и она оказывается равной:

Таким образом, фокальный параметр параболы совпадает с ее обычным параметром p, который равен расстоянию от фокуса до директрисы.

Еще одно свойство параболы можно получить, если провести наряду с параболой прямую, проходящую через начало отсчета. Уравнение этой прямой имеет вид y = kx.

При малых значениях x парабола лежит выше этой прямой, потому что x стремится к нулю быстрее, чем x. В то же время, каким бы малым не был бы угловой коэффициент, при достаточ- но больших значениях x парабола окажется ниже этой прямой. Действительно, для любого углового коэффициента существует решение уравнения, которое получается из равенства ординат параболы и прямой в точке пересечения:

241