Учебник

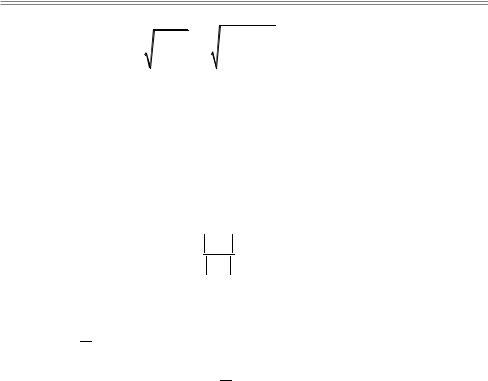
16. ЭЛЛИПС

16.1. Каноническое уравнение эллипса

Приведем определение эллипса как геометрического множества точек, то есть определение, независимое от системы координат.

Эллипс — это множество точек, сумма расстояний от которых до двух заданных точек (фокусов) постоянна.

Как и в случае с параболой, уравнение эллипса будет разным

âразных системах отсчета, а сам эллипс как геометрическая фигура не будет изменяться, то есть его форма и размеры в любой системе отсчета будут одинаковыми.

Получим уравнение для эллипса сначала в наиболее удобной для этого системе отсчета, которую выберем следующим образом. В начале предположим, что заданные фокусы различны и

обозначим их F1 è F2 . Тогда эти две точки однозначно определяют прямую, проходящую через них. Выберем эту прямую

âкачестве оси абсцисс нашей системы координат. Кроме того, однозначно определена и точка O — середина отрезка [F1F2 ], которую выберем в качестве начала отсчета. В качестве оси ор-

динат выберем прямую, проходящую через точку O и перпен- [F1F2 ]. Такая система отсчета с точностью

до замены направления осей на противоположные однозначно определяется двумя заданными фокусами эллипса и называется

канонической системой отсчета эллипса. Пример канонической системы отсчета приведен на рис. 16.1:

243

III. Кривые и поверхности второго порядка

MF1 + MF2 = 2a.

Обозначим расстояние между фокусами эллипса как 2c = F1F2 , тогда фокусы в этой системе отсчета будут иметь координаты F1 = (c,0) è F2 = (−c,0). Пусть некоторая точка M с координатами (x, y) принадлежит эллипсу. Тогда, вне зависимости от координат, сумма расстояний от точки M до фокусов, согласно определению, есть постоянная величина, которую мы обозначим как 2a :

Ðèñ. 16.1. Определение эллипса. Каноническая система отсчета эллипса

Точки F2 MF1 определяют треугольник, а согласно основному неравенству треугольника, длина каждой из его сторон меньше суммы длин двух других его сторон (см. задачу 5.2). В частности, F1F2 = 2c < MF1 + MF2 = 2a. Отсюда мы получаем одно из важных свойств эллипса:

Теперь перепишем уравнение (16.1) в координатном виде, используя выражения для расстояния между двумя точками через их координаты:

244

16. Эллипс

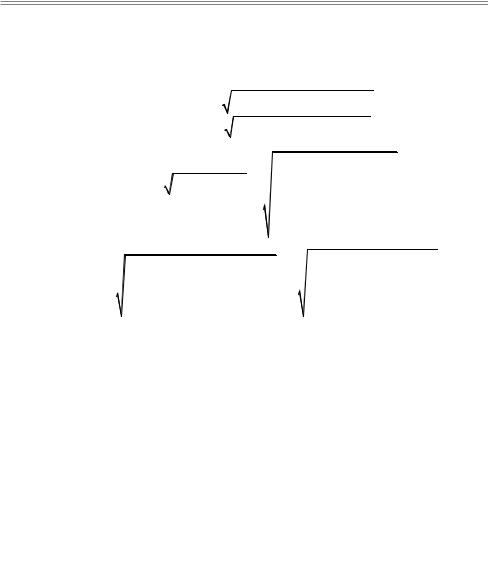
= (c − x)2 +(0 − y)2 +

+ (−c − x)2 +(0 − y)2 = (c − x)2 + y2 + (c + x)2 + y2 = 2a.

Чтобы избавиться от радикалов, мы умножим это равенство на разность радикалов, чтобы можно было воспользоваться формулой для разности квадратов:

((c − x)2 + y2 + (c + x)2 + y2 )((c + x)2 + y2 − (c − x)2 + y2 )= = 2a((c + x)2 + y2 − (c − x)2 + y2 )..

Откуда получаем, что

(c + x)2 + y2 −((c − x)2 + y2 )= 4xc = = 2a((c + x)2 + y2 − (c − x)2 + y2 ),

то есть разность корней равна

245

III. Кривые и поверхности второго порядка

Теперь собираем координаты в левой части

и вводим величину

b2 = a2 −c2 ,

которая положительна в силу неравенства (16.2) c < a. Тогда уравнение эллипса принимает вид

Мы получили так называемое каноническое уравнение эллипса. Исследуем свойства эллипса, исходя из его канонического уравнения.

16.2. Основные свойства эллипса

Анализ свойств эллипса как геометрической фигуры мы проведем, исходя из его уравнения, не сделав при этом ни одного геометрического измерения. В этом заключается преимущество аналитической геометрии, которая здесь, как и в случае с векторами, переводит геометрические понятия на язык алгебры.

Из канонического уравнения найдем выражение для перемен-

íîé x: x = ±a2 1− y2 . Отсюда следует, что x принимает значе- b2

íèÿ îò –a äî a, а переменная y — îò –b äî b:

−a ≤ x ≤ a,

−b ≤ y ≤ b.

Следовательно, эллипс как геометрическая фигура заключен внутри прямоугольника, стороны которого даются уравнениями x = ±a è y = ±b. Этот прямоугольник называется основным

246

16. Эллипс

прямоугольником эллипса. Средние кривые основного прямоугольника являются осями симметрии эллипса, которые совпадают с осями канонической системы координат. Наличие этих осей симметрии следует из того что, перемена знака координат не меняет самого уравнения.

шей. Поэтому величина a получила название большая полуось, а величина b — малая полуось. Точки эллипса, в которых абсолютные значения координат принимают свои максимальные значения x max = a è y max = b, называются вершинами эллипса. Вершины эллипса являются точками касания эллипса и его основного прямоугольника, и в то же время являются пересечениями эллипса со своими осями. Точка пересечения осей эллипса совпадает с началом отсчета канонической системы координат и является центром симметрии эллипса. Наличие центра симметрии следует из того, что одновременная перемена знака координат не меняет канонического уравнения:

Кроме того, наличие центра симметрии у любой фигуры следует из наличия двух перпендикулярных друг другу осей симметрии. Попробуйте это доказать самостоятельно.

Кроме того, мы будем также использовать понятие хорды эллипса как отрезка, соединяющего две точки эллипса. Хорду, проходящую через центр, называют диаметром эллипса. Среди диаметров эллипса выделяют большой диаметр, который совпадает с большой осью и проходит через оба фокуса, и малый диаметр, который совпадет с малой осью и перпендикулярен большому диаметру.

247

III. Кривые и поверхности второго порядка

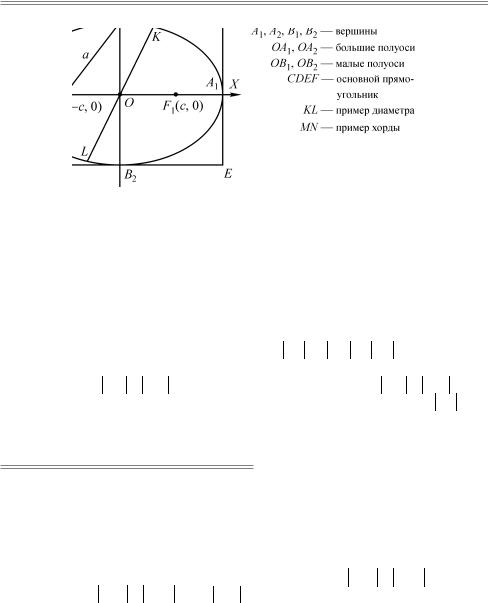
Ðèñ 16.2. Основные характеристики эллипса

На рис.16.2 отражены основные параметры эллипса, а также приведен пример отрезка [FB], соединяющего какой-либо фокус с какой-либо вершиной, лежащей на малой оси. Этот отрезок обладает интересным свойством — его длина совпадает с большой полуосью. Действительно, FB 2 = FO 2 + OB 2 = c2 +b2 ≡ a2 . Это же соотношение можно получить и другим способом. Так как F1B + F2 B ≡ 2a по определению эллипса, а F1B = F2 B из-за симметрии эллипса относительно оси OY , то, очевидно, FB = a.

16.3. Эллипс и окружность. Эксцентриситет эллипса

не определена однозначно, и в качестве оси абсцисс можно выбрать любую прямую, проходящую через точку O. Из определения эллипса в этом случае получаем F1M + F2 M = 2aF1M = F2M = a = OM , то есть эллипс образован точками, равноудаленными от точки O, а, следовательно, является окружностью. Так как окружность при поворотах вокруг своего центра переходит сама в себя, то становиться понятным, почему любая декартова система с центром в точке O является канонической для окружности.

248

16. Эллипс

В любой из таких систем отсчета уравнение окружности будет иметь вид

Это уравнение окружности можно записать в виде, принятом для записи канонического уравнения эллипса:

Таким образом, окружность является частным случаем эллипса. Теперь давайте «растянем» одну из осей координат (другими

словами, изменим масштаб), например, ось ординат: y → y ' = ky.

В новых координатах уравнение окружности примет вид:

то есть оно перейдет в уравнение эллипса. По этой причине про эллипс часто говорят, что эллипс — это сжатая окружность.

Ðèñ. 16.3. Переход окружности в эллипс при сжатии. Преобразование вращательного движения эллипса вокруг фокуса в поступательное

249

III. Кривые и поверхности второго порядка

Степень отличия эллипса от окружности, или степень сжатия эллипса, можно было бы определять отношением большой и малой полуосей a / b, которая равнялась бы единице у окружности. Однако, общепринятым параметром, который отличает эллипс от окружности, является отношение расстояния между фокуса-

22ac , которое у окружности равно нулю. Этот параметр получил название эксцентриситета эллипса:

Он описывает отклонение центра эллипса от его фокуса, то есть определяет своеобразную «расцентровку» эллипса. Отличие от нуля эксцентриситета эллипса можно использовать при преобразовании вращательного движения эллипса вокруг фокуса в поступательное движение, которое совершает при этом, в частности, точка, максимально удаленная в выбранном направлении от этого фокуса.

Используя связь между полуосями, можно получить еще одно выражение для эксцентриситета:

которое позволяет находить эксцентриситет прямо из параметров канонического уравнения.

16.4. Определение эллипса с помощью директрисы и эксцентриситета

Проведем через фокус эллипса хорду, перпендикулярную большой полуоси, например, отрезок NN1 на рис. 16.4. Это так называемая фокальная хорда, и половину ее длины можно найти прямо из канонического уравнения как ординату точки N, абсцисса которой равна абсциссе фокуса xN = xF1 = c. Òî åñòü:

250

16. Эллипс

Эта величина для эллипса носит такое же название, что и для параболы: фокальный параметр, и обозначается той же буквой:

Фокальный параметр, как и эксцентриситет, является одним из общих характеристик парабол, эллипсов и гипербол.

e = MF1 ML

Теперь проведем прямую, перпендикулярную большой оси эллипса и лежащую вне основного прямоугольника эллипса на

расстоянии ep от ближайшего фокуса:

F1D1 = ep ,

ãäå D1 — точка пересечения этой прямой и оси эллипса.

Эта прямая называется директрисой эллипса. Уравнение этой и симметричной ей директрисы имеют вид:

в чем можно убедиться, если найти расстояние от директрис до начал отсчета:

251

III. Кривые и поверхности второго порядка

Оно равно эксцентриситету и не зависит от координаты! При выводе мы использовали каноническое уравнение эллипса, связь между полуосями и определение эксцентриситета.

Рисунок 16.4. Директрисы и параметр эллипса. Определение эллипса через директрису и эксцентриситет

Мы видим, что для всех точек эллипса справедливо следующее правило: отношение расстояния от любой точки эллипса до

252