§1.4. Свободные колебания в динамических системах с распределенными элементами

В технике радиосвязи, радиолокации, в устройствах техники СВЧ, микроэлектроники и других широкое применение получили элементы, у которых размеры сравнимы или больше длины волны l>λ, К таким элементам относятся линии передачи энергии (двухпроводные, коаксиальные и микрополосковые линии, волноводы и др.).

Электрические цепи, для которых волновой характер процесса представляет основу используемых свойств цепи, а замена распреде­ленных элементов сосредоточенными приводит к утрате этих основ­ных свойств цепи, называют цепями с распределенными элементами. Токи и напряжения в таких цепях являются функциями координат сечения наблюдения цепи и времени t.

При составлении систем уравнений с распределенными элемен­тами возникают трудности: I) не выполняются законы Кирхгофа; 2) очень сложно произвести выбор реальной модели цепи с распре­деленными элементами; 3) напряжения и токи зависят не только от времени, но и от пространственных координат.

В связи с тем, что линии передачи сигналов являются состав­ной частью радиотехнической цепи, для анализа и синтеза которой необходимо знать напряжение и токи в линиях, широкое примене­ние получили методы теории электрических цепей. Возможность при­менения указанных методов основывается на представлении о линии в виде цепи с большим числом бесконечно малых по величине пассив­ных элементов или, иными словами, о линии как о цепи с распре­деленными (по ее длине) элементами. В соответствии с этим исполь­зуются понятия о так называемых погонных (распределенных) пара­метрах линии: резистивном сопротивлении R₀, индуктивности L₀ , емкости С₀ и проводимости G_o единицы длины линии. Их значения находят в общем случае методами теории электромаг­нитного поля.

Дифференциальные уравнения, связывающие в некоторый момент мгновенные значения токов и напряжений, имеют следующий вид:

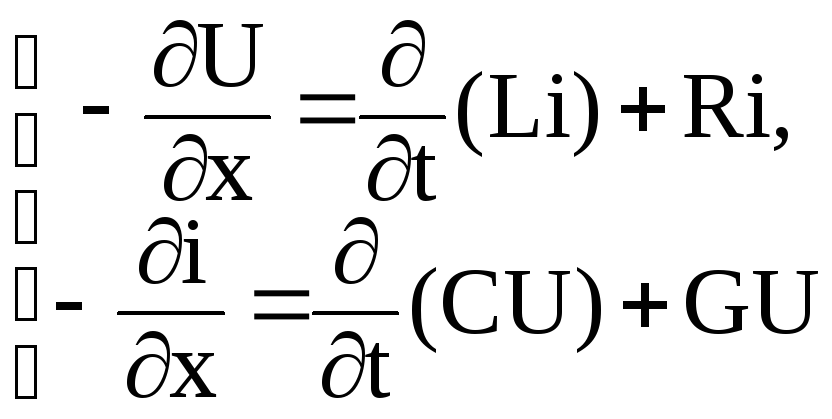
и часто называются телеграфными уравнениями, что обусловлено исторически, когда впервые применили линии связи для передачи телеграфных сигналов. Совместное решение дифференциальных урав­нений в частных производных при заданных начальных и граничных условиях позволяет в каждом конкретном случае решить поставлен­ную задачу на отыскание мгновенных значений токов и напряжений в линии.

§1.4.1.Классификация длинных линий

Если погонные параметры линии R, L, С и G посто­янные во времени и пространстве величины, то такую линию назы­вают однородной в пространстве и инвариантной во времени линейной линией.

Если погонные параметры R, L, С и G зависят от времени, линия называется параметрической.

Если параметры R, L, С и G представляют собой функ­ции напряжения U и тока

i , то такая линия называется нели­нейной.

§1.4.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом

Несмотря на внешнюю простоту телеграфных уравнений, их ана­литическое решение для произвольных сопротивлений генератора и нагрузки и сигнала произвольной формы отсутствует. Применение операторного метода, как было показано ранее, позволяет суще­ственно упростить отыскание мгновенных значений напряжения U(x,t) и тока i (x,t ).

Ограничимся рассмотрением линейной, однородной, инвариант­ной во времени длинной линией. В этом случае уравнение будет иметь вид:

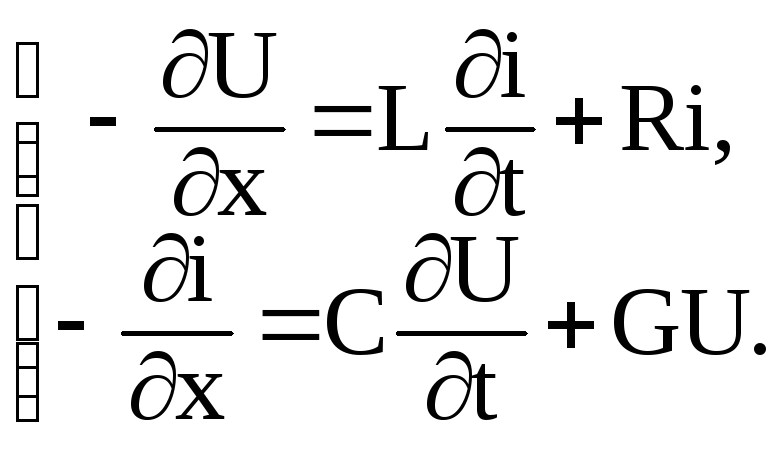
Напряжение U (x,t ) и токи i (x,t ) в длинной линии, а также источники, как и ранее удовлетворяют условию принадлежности к классу оригиналов.

В этом случае

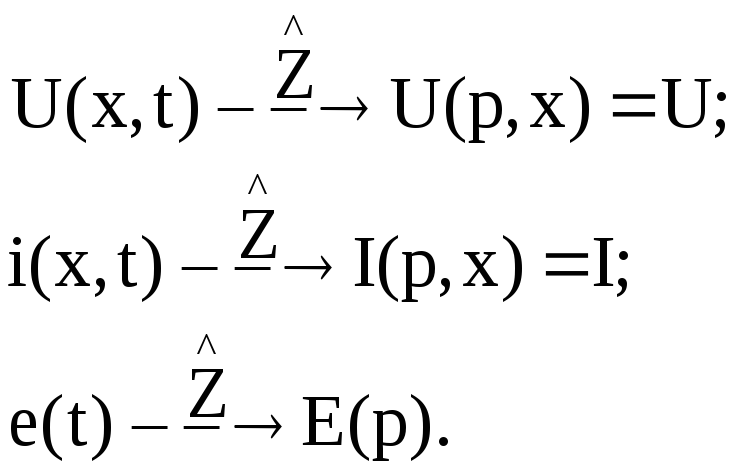
Применяя преобразование Лапласа к системе уравнений, получим систему операторных уравнений в полных производных:

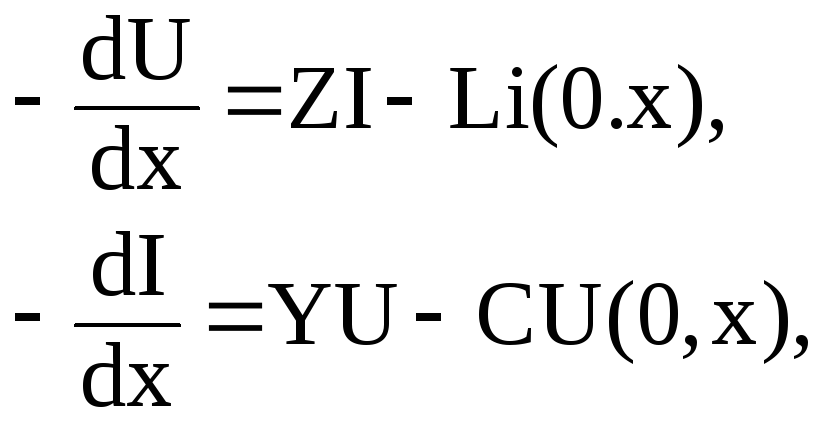
где Z=pL + R; Y=рC+G ; либо одно дифференциальное уравнение второго порядка:

где - операторная постоянная распространения волны;- функция начальных условий. Решение уравненияU (x_, p) состоит из общего решения однородного дифференциального уравнения и какого либо частного решения:

U(p,x)=A₁e^-γx+ A₂e^γx+U⁰.

Тогда из первого уравнения системы находим:

где - операторное волновое сопротивление; коэффициентыА₁(р) и A₂(р) определя­ются из граничных условий.

Решение операторной системы уравнений для изображения на­пряжения U(р,x) и тока I(р,x) найдено. Осуществив обратное преобразование Лапласа, восстанавливают оригиналы на­пряжения U( x, t) и тока I(х,t ). Однако решение в об­щем случае отыскать не удается. Рассмотрим некоторые частные случаи.

Линия без потерь

В этом случае R=G= 0 и . Тогда

Осуществляя обратное преобразование Лапласа, получим:

где

Следовательно, решение представляется в виде суммы прямой и обратной волны .

Линия без искажений

Для данной линии характерно выполнение соотношения .Следовательно,

Изображение напряжения в линии есть

Осуществляя обратное преобразование Лапласа, получим:

Следовательно, для линии без искажений мгновенные значения напряжения и тока представляют собой наложение прямой и обратной волн, затухающих в процессе распространения. Для линейных цепей с распределенными параметрами справедлив принцип наложения, и, следовательно, задачи анализа свободных и вынуж­денных колебаний могут рассматриваться порознь, аналогично це­пям с сосредоточенными параметрами.