
- •Глава 1.
- •§1.1.Преобразование Лапласа и его основные свойства.
- •§ 1.2. Применение операторного метода для анализа процессов в цепях сосредоточенными элементами.
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях.
- •§1.4. Свободные колебания в динамических системах с распределенными элементами
- •§1.4.1.Классификация длинных линий
- •§1.4.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •§1.4.Алгоритмы решения задачи о собственных колебаниях в длинной линии
- •Глава 2. Колебания в линейных праметричеких
- •§ 2.1. Линейные спектра входного сигнала, при прохождении через линейные параметрические цепи.
- •§ 2.2. Аксиоматики теории цепей в параметрическом случае.
- •§2.3. Прохождение сигналов через параметрические r – цепи.
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с обной степенью свободы. Энергетическое рассотрение стационарных колебаний в системах с одной степенью свободы.
- •§ 2.5.1. Процессы в параметрической колебательной системе с обной степенью свободы.
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы.
- •§2.5.Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье.
- •2.6. Параметрическое усиление колебаний в одноконтурной системе.
- •§2.2.4 Параметрический генератор(параметрон).
- •§2.2. Двухконтурные параметрические системы.
- •§2.2.1Теорема Менли-Роу.
- •§ 2.2.2 Параметрические умножение и деление частоты.
- •§2.4. Некоторые приближенные методы исследования процессов в. Параметрических системах
- •§2.4.1. Метод «замороженного» параметра.
- •§2.4.1 Метод замороженного параметра.(второй вариант).
- •§2.4.2 Метод последовательных приближений.
- •§2.4.2. Метод последовательных приближений (второй вариант).
- •§2.4.3 Метод вкб.
- •§2.4.3. Метод вкб (Вентцеля-Крамерса-Бриллюэна)(второй вариант).
- •Глава 3. Анализ колебаний в нелинейных цепях.
- •3.1 Нелинейные элементы цепей
- •§3.2.Особенности задач анализа колебаний в нелинейных цепях.
- •§3.3. Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений.
- •§3.4. Метод линеаризации.
- •§3.2. Метод гармонической линеаризации (мгл).
- •§3.2.1. Эквивалентные параметры нелинейных элементов.
- •§3.3.Методы малого параметра. Метод последовательных приближений.
- •§3.4.Метод медленно меняющихся амплитуд (ммма).
- •§3.5.Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде.
- •§3.6.Метод фазовой плоскости.
- •1.Метод изоклин.
- •2.Особые точки.
§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях.
Рассмотрим цепь, в которой в момент времени t=0 возбуждаются свободные колебания. Они обусловлены напряжениями, до которых в момент t=0 заряжены емкости цепи – uC(0) и токами протекающими в тот же момент через индуктивность – iL(0). Совокупность значений uC(0) и iL(0) составляет начальные условия задачи, которые при записи системы уравнений в операторной форме определяет правые части уравнений. Видно, что определение свободных колебаний в цепи является по существу задачей Коши.
Пусть среди всех колебаний напряжений и токов в цепи нас интересует одно Sвых(t), находящееся, например, в k-й части цепи. Решая систему уравнений по правилу Крамера, получим решение для искомого изображения в виде
Sвых(p)=![]() (1.29)
(1.29)
где ∆(p) и ∆k(p) – определители системы, составленные по правилу Крамера; A(p) – сомножитель, присутствующий в тех случаях, когда размерность искомого колебания отлична от размерности функций, выбранных в качестве исходных при составлении системы уравнений. Выражение для Sвых(p) является дробно-рациональной функцией
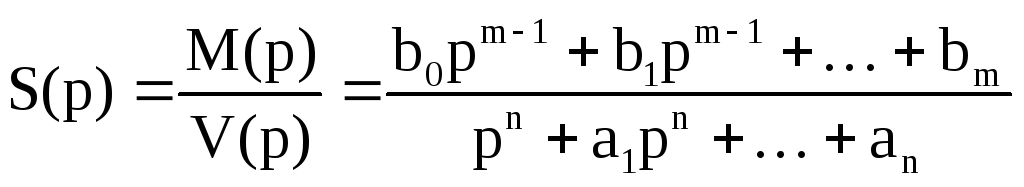 ,
(1.30)
,
(1.30)
причем m≤n, bk и ak – действительные числа.
V(p) – характеристический многочлен электрической цепи. Его корни полностью определяют характер решения – собственные колебания. M(p) – многочлен, определяющий конкретное свободное колебания, порожденное конкретными начальники условиями.
Искомое свободное колебание Sвых(p) находим, осуществляя обратное преобразование Лапласа.
Ограничимся
важным для практики случаем, когда корни
характеристического многочлена V(p) не
имеют кратных корней, иначе решение
получается более громоздким, но не
содержащим принципиально ничего нового
по сравнению с рассматриваемым случаем.
Поскольку коэффициенты a1,
a2
… an,
многочлена V(p) вещественны, его корни
принимают действительные pk
и попарно
комплексно-сопряженные
![]() и
и![]() значения. Причем в случае пассивных
устойчивых цепей действительные части
корней многочлена являются отрицательными
величинами
значения. Причем в случае пассивных
устойчивых цепей действительные части
корней многочлена являются отрицательными
величинами![]() ;
;![]() ;
;![]() .
Тогда решение задачи, определяемое
выражением
.
Тогда решение задачи, определяемое
выражением
![]()
![]()
![]() (t≥0),
(1.31)
(t≥0),
(1.31)
приводит
к виду![]()
![]() соs(ωlt+φl),
(t≥0)
(1.32)
соs(ωlt+φl),
(t≥0)
(1.32)
где
первая сумма соответствует действительным
корням pk=
- δk
и описывает
экспоненциально убывающие составляющие
свободных колебаний. Вторая сумма
соответствует парам комплексно-сопряженных
корней и описывает убывающие колебательные
составляющие.
![]() ,
,![]() ψl=arg
ψl=arg![]() .
Из полученного выражения видно, что
свободные колебания в устойчивых цепях
состоят из совокупности убывающих
составляющих и в целом являются
затухающими.
.
Из полученного выражения видно, что
свободные колебания в устойчивых цепях
состоят из совокупности убывающих
составляющих и в целом являются
затухающими.
В случае кратных корней решение имеет более громоздкий вид, но ничего нового принципиально не содержит. Если характеристический полином V(p) имеет кратные нули, тогда Sвых(t) представляется следующей суммой
Sвых(t)=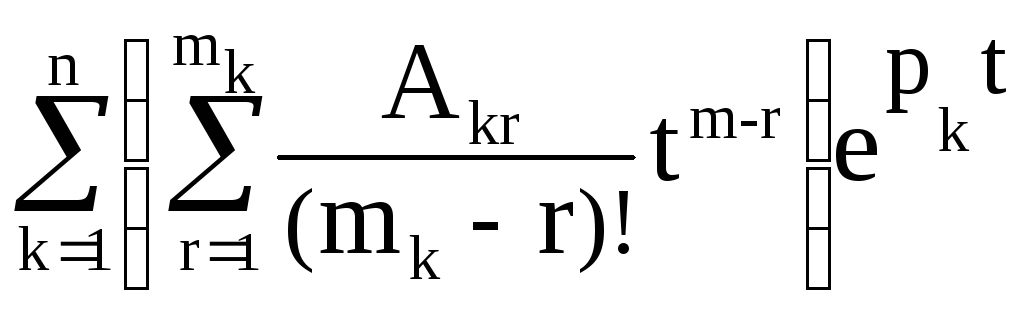 , (t
≥ 0),
, (t
≥ 0),
где mk – кратность k-го нуля,
Akr
=
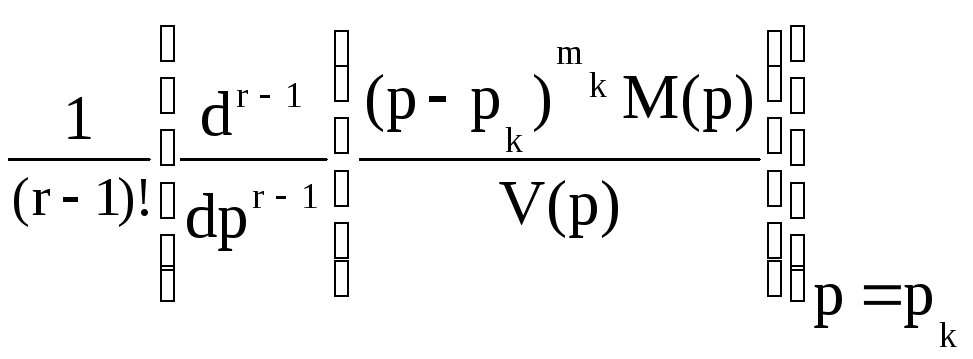 .
.
Каждому m - кратному нулю, лежащему на действительной оси, в этой сумме соответствует группа слагаемых вида
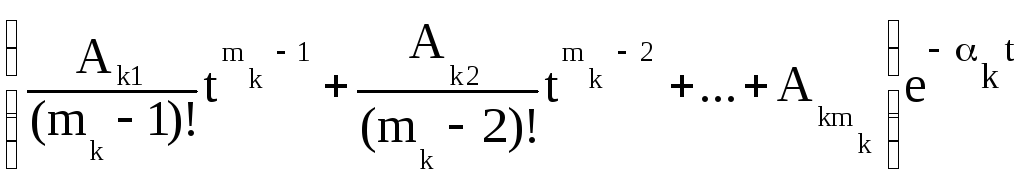 ,
,
а каждой m – кратной паре комплексно-сопряженных нулей – группа слагаемых вида
2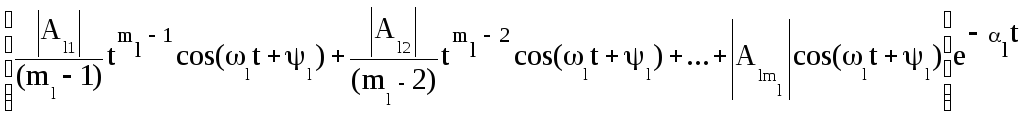
Корни характеристического уравнения V(p) = 0 имеют отрицательные вещественные части тогда и только тогда, когда положительны все определители последовательности
В цепях составленных из элементов активного сопротивления, корни характеристического многочлена цепи V(p) являются чисто мнимыми pl=iωl. А свободные колебания описываются выражением
![]() ,
(1.33)
,
(1.33)
которому соответствуют незатухающие стационарные колебания.
Если хоть у одной пары комплексно-сопряженных корней характеристического многочлена некоторой цепи V(p) действительная часть окажется положительной, pl =+δl± iωl, то в решении появится нарастающая колебательная составляющая Sleδltcos(ωlt+ψl). Цепи, для которых это имеет место, называют неустойчивыми. К их числу относятся всевозможные автогенераторы. В своем составе эти цепи обязательно должны иметь дополнительные источники энергии и электронные приборы (ЭП). Следует заметить, однако, что линейная теория неустойчивых цепей является верной, пока колебания в цепи настолько малы, что они не выходят за пределы линейных областей характеристик ЭП.
Одной из важнейших задач, возникающих при проектировании самых разнообразных цепей, является задача определения принадлежности цепи к устойчивым или неустойчивым цепям. Видно, что эта задача сводится к исследованию расположения корней характеристического многочлена цепи V(p) на комплексной плоскости. Если все корни V(p) располагаются в левой полуплоскости – цепь устойчива.
Методы, с помощью которых можно судить об устойчивости цепи не прибегая к вычислению корней ее характеристического многочлена, называется критериями устойчивости. Один из них – критерий устойчивости Раусса-Гурвица – формулируется следующим образом.
Корни характеристического уравнения V(p)=0 имеют отрицательные вещественные части тогда и только тогда, когда положительны все определители последовательности
Δ1=a1;
Δ2=![]() ;
Δ3=
;
Δ3=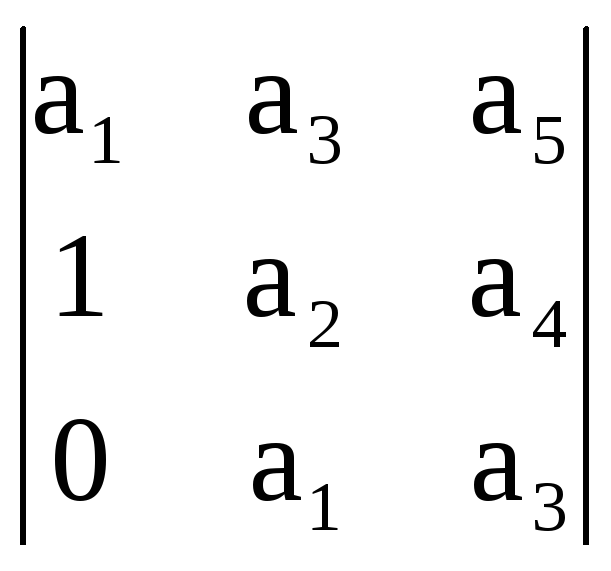 ;
;
![]() ;
Δn=
;
Δn= ;
(1.34)
;
(1.34)
Алгоритм решения задачи анализа свободных колебаний
Анализируя состояние цепи в момент времени t=0 определяем начальные условия – совокупность значений величин uc(0) и il(0).
Составляем схему цепи в операторных величинах. Ненулевые начальные условия в схеме будут отражены источниками с соответствующими операторными задающими характеристиками.
Выбираем метод и записываем систему уравнений (одно уравнение) в операторной форме.
Находим решение уравнений и представляем изображение искомого колебания в виде отношения многочленов.
Исследуем характеристический многочлен. При необходимости используем критерий устойчивости Раусса-Гурвица.
На основании общего вида решения задачи анализа, в зависимости от расположения корней V(p), определяем структуру решения.
Определяем коэффициенты решения и записываем его в окончательном виде. Строим график полученной функции.
Анализируем полученный результат.
Примеры анализа свободного колебаний
Пример 1. Контур ударного возбуждения
Пусть
в цепи рис.1 в момент времени t=0
электронный прибор, работающий в ключевом
режиме, запирается управляющим сигналом.
До запирания ток инжекторного электрода
равен I0.
Пренебрегая влиянием разделительной
емкости Cp
(т.к. Cp![]() C)
найти выходное напряжение Uвых(t)
при t
C)
найти выходное напряжение Uвых(t)
при t![]() 0.
Eп
0.
Eп
О
 пределяем
начальные условия
пределяем
начальные условия





















 к
к
Sупр у il(0)= I0; uc(0)= 0
и
I0 Cp




![]() L
C
R
Uвых(t)
L
C
R
Uвых(t)
Составляем схему в операторных параметрах


![]()













![]() pL
pL
![]() R U(p) = Uвых(p)
R U(p) = Uвых(p)
Записываем узловое уравнение для изображений
![]() (pC
+ G + 1
(pC
+ G + 1![]() pL
) U(p) = I0
⁄
p.
pL
) U(p) = I0
⁄
p.
Записываем решение уравнения
U(p)
=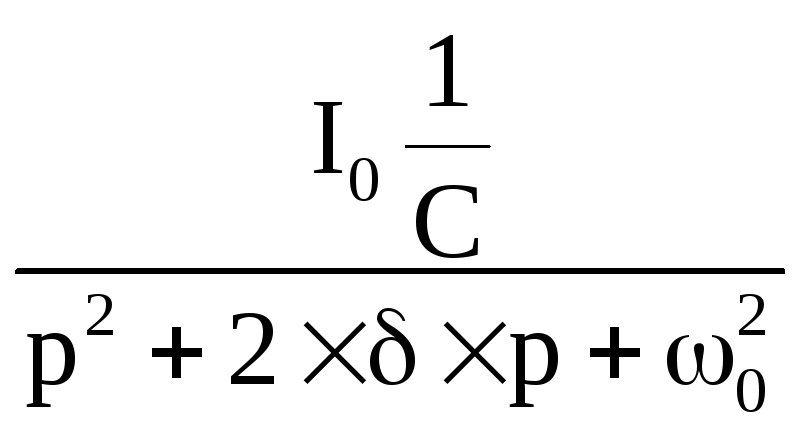 ,
где
,
где
![]()
![]() 0;
0;
![]() >0.
>0.
Исследуем характеристический многочлен V(p)= p2 + 2δp +
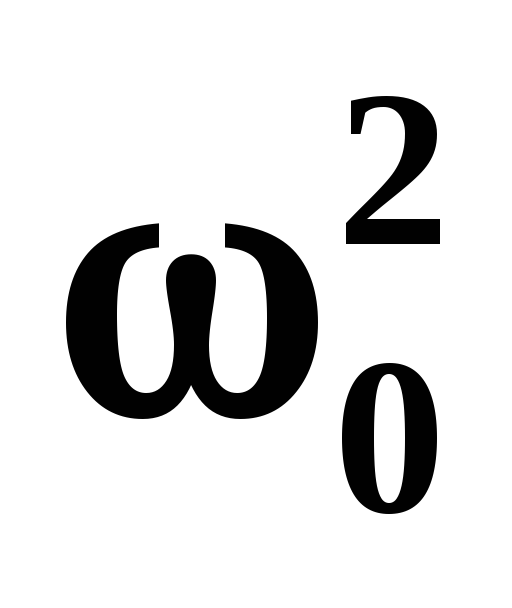 .Его корни p1,2= -δ
± ±
.Его корни p1,2= -δ
± ±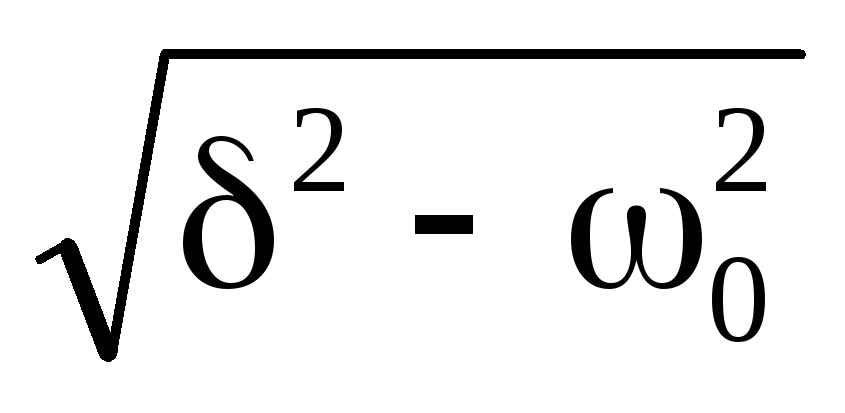 при условии
при условии (контур колебательный) являются парой
комплексно-сопряженных величинp1,2= -
(контур колебательный) являются парой
комплексно-сопряженных величинp1,2= - ,
где
,
где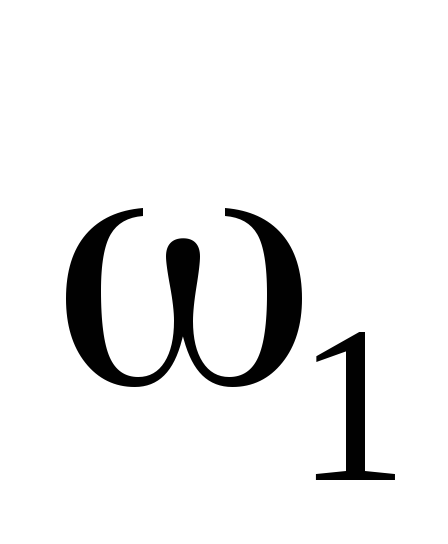 =
=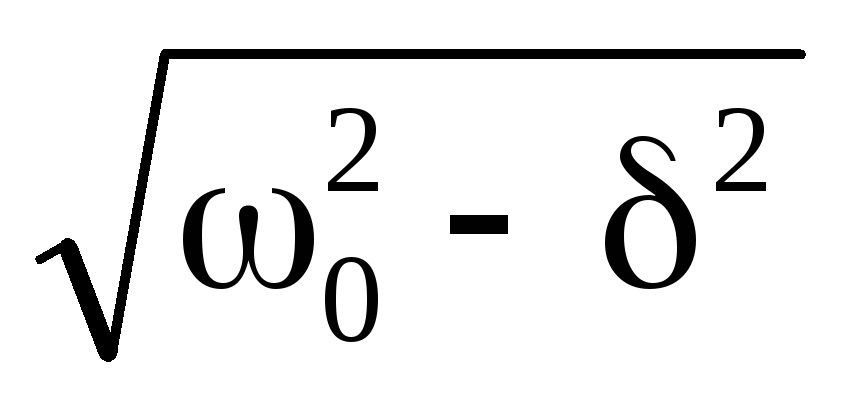 .
Вещественная часть корней – отрицательная,
следовательно цепь является устойчивой.
.
Вещественная часть корней – отрицательная,
следовательно цепь является устойчивой.На основании общего решения задачи о свободных колебаниях записываем структуру решения
Uвых(t) = U1e
–δtcos (ω1t + ψ1) , (t![]() 0).
0).
Определяем коэффициенты решения U1 и ψ1
U1
= 2![]() =
=![]() ; ψ1
= arg
; ψ1
= arg
![]() = -
= -![]() .
.
Записываем решение в окончательном виде
Uвых=![]() ,
(t
,
(t![]()
![]() 0 ).
0 ).
Анализируем полученный результат. Выходной сигнал Uвых(t) (рис. 2) представляет собой затухающее синусоидальное колебание начальная амплитуда которого, пропорциональна начальному току I0, частота
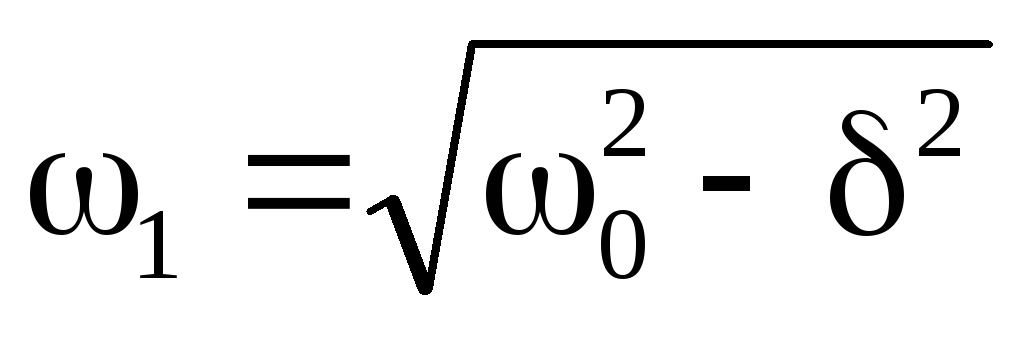 меньше
резонансного значения ω0; скорость
убывания колебаний тем меньше, чем
больше R (чем выше добротность колебательной
системы) и т.д.
меньше
резонансного значения ω0; скорость
убывания колебаний тем меньше, чем
больше R (чем выше добротность колебательной
системы) и т.д.
 Uвых(t)
Uвых(t)
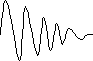

![]()
 t
t
Рис. 2
Пример 2 НАЧАЛЬНАЯ СТАДИЯ РАЗВИТИЯ КОЛЕБАНИЙ В АВТОГЕНЕРАТОРЕ.
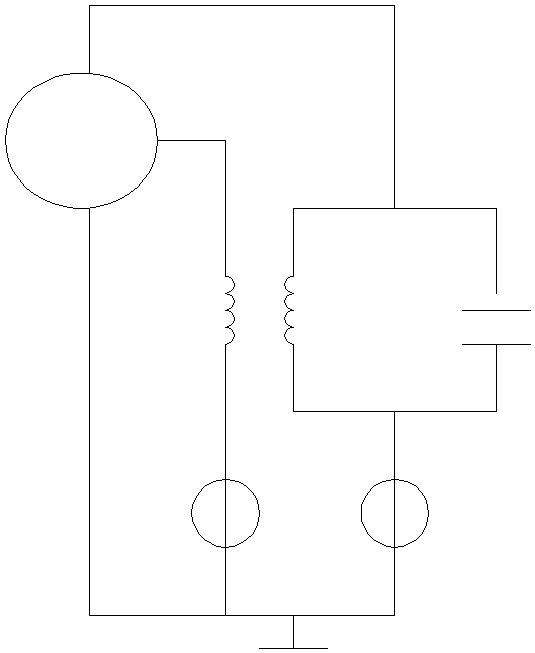
Данная цель – резонансный усилительный каскад с положительной обратной связью (рис.3.). Найти условия, при которых в цепи возникают автоколебания, и определить их характер.
 1.
Начальные условия – нулевые, но
предположим,
1.
Начальные условия – нулевые, но
предположим,
к у что в момент времени t = 0 произошло очень малое
 ЭП n
изменение тока ЭП и, следовательно, тока
индуктив-
ЭП n
изменение тока ЭП и, следовательно, тока
индуктив-
.ности. Пусть изображение этой флуктуацииJ0(t).
и L C Uвых(t) 2. Составляем схему цепи в операторных параметрах














 knу
knу
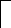 EсмEпит-SUу-n(p).
EсмEпит-SUу-n(p).
U(p)
Ri
![]() pL Uу-n(p)=
pL Uу-n(p)=
 .
.
Рис. 3.
n
3. Записываем узловое уравнение
(
pC + Gi
+
![]() )
U(p) = nSU(p) + J0(p)
.
)
U(p) = nSU(p) + J0(p)
.
Преобразуем его к виду
( pC +
Gi -
nS +
![]() )
U(p) = J0(p)
.
)
U(p) = J0(p)
.
4. Записываем решение уравнения
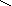
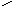
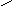
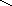 U(p) =
U(p) =
![]() , где
, где
![]() 0;
0;
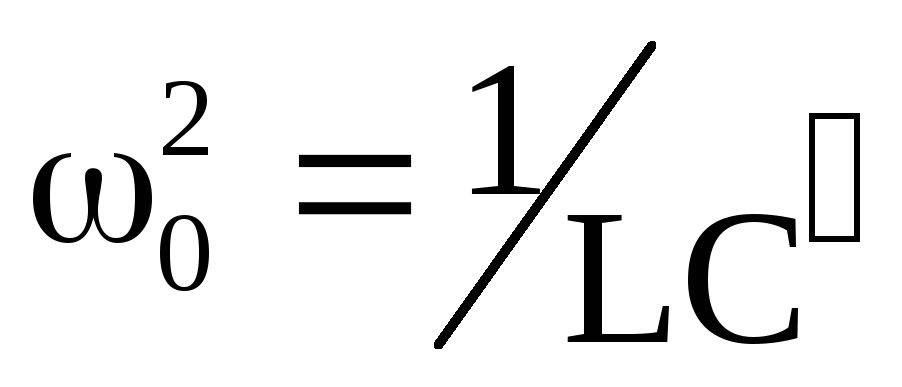 0.
0.
5. Исследуем
характеристический многочлен V(p) = p2
+ 2δp +![]() .
Его корни
.
Его корни
p1,2 = -![]() при условии
при условии![]() (контур колебательный) являются парой
комплексно сопряженных величин
(контур колебательный) являются парой
комплексно сопряженных величин![]() ,
где
,
где![]() .
При G
.
При G![]() nS
действительная часть корней отрицательна
и, следовательно, цепь устойчива. При
G
nS
действительная часть корней отрицательна
и, следовательно, цепь устойчива. При
G![]() nS действительная часть корней
положительна, цепь неустойчива, а
свободные колебания описываются
выражением
nS действительная часть корней
положительна, цепь неустойчива, а
свободные колебания описываются
выражением
U(p) =U1![]() ,(t
,(t
![]() 0).
0).
Анализируем полученные результаты. Если G
 nS,
то свободные колебания носят
затухающий характер и цепь в этом случае
является регенеративным усилителем.
Если жеG
nS,
то свободные колебания носят
затухающий характер и цепь в этом случае
является регенеративным усилителем.
Если жеG nS, то свободные колебания экспоненциально
нарастают от сколь угодно малой величины,
до значений, при которых наступает
ограничение амплитуды колебаний,
связанное с нелинейными областями ВАХ
ЭП (рис.4.). Скорость нарастания колебаний
тем больше, чем большеSиn, в этом случае цепь,
является генератором гармонических
колебаний частоты ω0.
nS, то свободные колебания экспоненциально
нарастают от сколь угодно малой величины,
до значений, при которых наступает
ограничение амплитуды колебаний,
связанное с нелинейными областями ВАХ
ЭП (рис.4.). Скорость нарастания колебаний
тем больше, чем большеSиn, в этом случае цепь,
является генератором гармонических
колебаний частоты ω0.
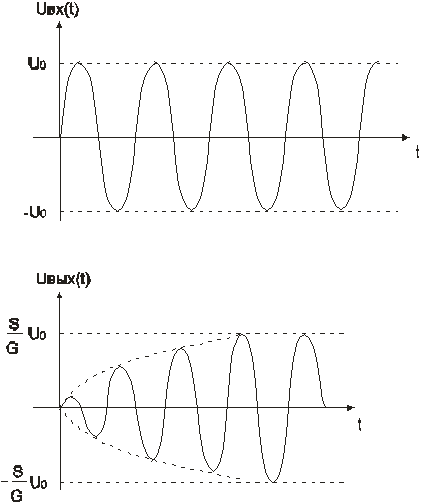
Рис.4
7. Анализируем полученный результат.
Сомножитель
![]() - есть
не что иное, как коэффициент усиления
на резонансной частоте.
- есть
не что иное, как коэффициент усиления
на резонансной частоте.
Выходные колебания устанавливаются не сразу. Причем чем больше Q, тем меньше δ, тем медленнее происходит процесс установления выходных колебаний и т.п.
