- •Глава 1.
- •§1.1.Преобразование Лапласа и его основные свойства.
- •§ 1.2. Применение операторного метода для анализа процессов в цепях сосредоточенными элементами.
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях.
- •§1.4. Свободные колебания в динамических системах с распределенными элементами
- •§1.4.1.Классификация длинных линий
- •§1.4.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •§1.4.Алгоритмы решения задачи о собственных колебаниях в длинной линии
- •Глава 2. Колебания в линейных праметричеких
- •§ 2.1. Линейные спектра входного сигнала, при прохождении через линейные параметрические цепи.
- •§ 2.2. Аксиоматики теории цепей в параметрическом случае.
- •§2.3. Прохождение сигналов через параметрические r – цепи.
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с обной степенью свободы. Энергетическое рассотрение стационарных колебаний в системах с одной степенью свободы.
- •§ 2.5.1. Процессы в параметрической колебательной системе с обной степенью свободы.
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы.
- •§2.5.Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье.
- •2.6. Параметрическое усиление колебаний в одноконтурной системе.
- •§2.2.4 Параметрический генератор(параметрон).
- •§2.2. Двухконтурные параметрические системы.
- •§2.2.1Теорема Менли-Роу.
- •§ 2.2.2 Параметрические умножение и деление частоты.
- •§2.4. Некоторые приближенные методы исследования процессов в. Параметрических системах
- •§2.4.1. Метод «замороженного» параметра.
- •§2.4.1 Метод замороженного параметра.(второй вариант).
- •§2.4.2 Метод последовательных приближений.
- •§2.4.2. Метод последовательных приближений (второй вариант).
- •§2.4.3 Метод вкб.
- •§2.4.3. Метод вкб (Вентцеля-Крамерса-Бриллюэна)(второй вариант).
- •Глава 3. Анализ колебаний в нелинейных цепях.
- •3.1 Нелинейные элементы цепей
- •§3.2.Особенности задач анализа колебаний в нелинейных цепях.
- •§3.3. Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений.
- •§3.4. Метод линеаризации.
- •§3.2. Метод гармонической линеаризации (мгл).
- •§3.2.1. Эквивалентные параметры нелинейных элементов.
- •§3.3.Методы малого параметра. Метод последовательных приближений.
- •§3.4.Метод медленно меняющихся амплитуд (ммма).
- •§3.5.Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде.
- •§3.6.Метод фазовой плоскости.
- •1.Метод изоклин.
- •2.Особые точки.
1.Метод изоклин.
 Поскольку
последнее уравнение, так же как и
предыдущее не удается решить аналитически,
прибегают к построению фазовых траекторий
методом изоклин. Для этого полагают,
что
Поскольку
последнее уравнение, так же как и
предыдущее не удается решить аналитически,
прибегают к построению фазовых траекторий
методом изоклин. Для этого полагают,
что
![]() ,
и задавая различные значения одной из
величинx
или y
можно рассчитать и построить на фазовой
плоскости график функции
,
и задавая различные значения одной из
величинx
или y
можно рассчитать и построить на фазовой
плоскости график функции
![]() , называемой изоклиной, т.к. она определяет
линии проходящие через интегральные
кривые в точках с одинаковым углом
наклона
, называемой изоклиной, т.к. она определяет
линии проходящие через интегральные
кривые в точках с одинаковым углом
наклона![]() =tg
α
.
=tg
α
.
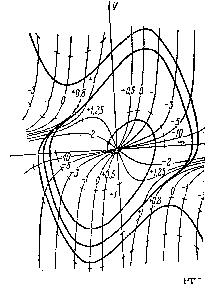
Изменяя значения соnst (от - ∞ до + ∞ ) можно построить поле изоклин, а после этого построить фазовый портрет. Например, для уравнения Ван-дер-Поля
![]()
Рис. 1. поле изоклин и фазовые портреты имеют вид.
2.Особые точки.
Заполнение фазовой плоскости полем направлений – трудоемкий процесс. Поэтому, часто для определения характера фазовых траекторий, используют метод, основанный на построении особых точек и особых линий. Общее количество особых точек невелико, характер фазовых траекторий вблизи них хорошо изучен. Если еще удается построить предельные циклы и сепаратриссы, что является очень трудоемкой задачей, то вид фазовых траекторий на плоскости удается установить без построения изоклин. ″До сих пор не существует достаточно общих теоретических методов для решения вопроса о существовании предельных циклов и определения места их расположения, за исключением случая систем, близких к линейным (ε « 1)″. (Боголюбов Н.Н., Митропольский Ю.А. «Асимптотические методы в теории нелинейных колебаний»).
Для
определения координат особых точек
вспомним определение, что через эту
точку проходит либо много фазовых
траекторий, либо ни одной. Это значит,
что в этой точке не определена фазовая
скорость vф
=
![]() ,
а это возможно если одновременно
равняется нулю
,
а это возможно если одновременно
равняется нулю![]() и
и![]() .
Тогда для определения координат особых
точек на фазовой плоскости необходимо
решить систему уравнений:
.
Тогда для определения координат особых
точек на фазовой плоскости необходимо
решить систему уравнений:
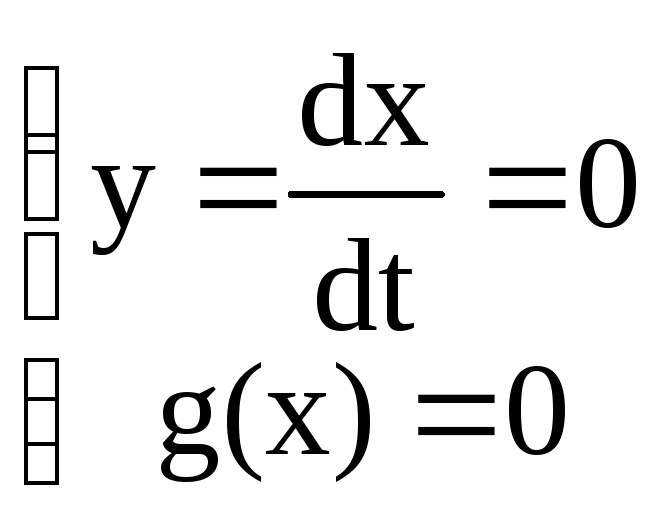 для
случая, когда колебания задаются одним
уравнением 2го
порядка (1) и
для
случая, когда колебания задаются одним
уравнением 2го
порядка (1) и
![]() для
случая, когда колебания задаются системой
уравнений (4).
для
случая, когда колебания задаются системой
уравнений (4).
Если рассматривать малые области отклонения колебаний вокруг особых точек, то уравнения описывающие колебания, можно линеаризовать, и по полученному виду определить характер особой точки. После линеаризации дифференциальное уравнение (1) принимает вид
![]() .
(5)
.
(5)
Т.к.
это уравнение линейное, то для его
анализа можно применять любой из методов
теории линейных цепей, например,
операторный метод. Тогда характеристическое
уравнение для уравнения (5) имеет вид:
p2
+ a1
p
+ a2
= 0. Корни характеристического уравнения
(5) равняются: p1,2
= –
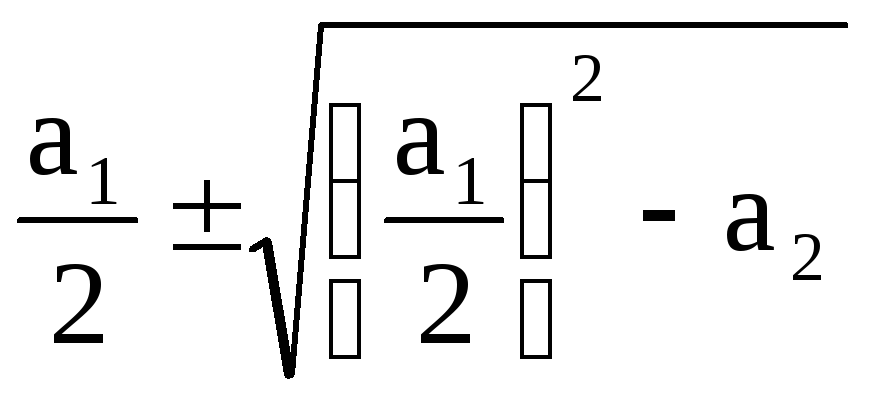 - могут принимать различные значения в
зависимости от знаков и величин
коэффициентов а1
и а2
.
- могут принимать различные значения в
зависимости от знаков и величин
коэффициентов а1
и а2
.
1). а1 = 0; а2 › 0.
Тогда
p1,2
= ± j
ω;
( где ω =
![]() ),
а колебания переменных имеют вид
),
а колебания переменных имеют вид
 .
.
Тогда
исключая из уравнений явно содержащееся
время t,
получим уравнение относительно переменных
y(x):
![]() ,
которое описывает в качестве фазовых
траекторий вложенные в друг друга
эллипсы (замкнутые траектории, т.е
периодические колебания).
,
которое описывает в качестве фазовых
траекторий вложенные в друг друга
эллипсы (замкнутые траектории, т.е
периодические колебания).
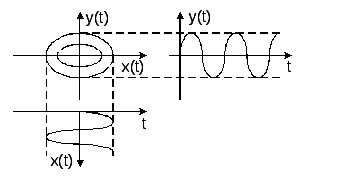
Особая точка типа центр
Рис.2.
2).а1
› 0; а2
› 0; а2
› (![]() )2
. Корни характеристического полинома
для этого случая равны:
)2
. Корни характеристического полинома
для этого случая равны:
p1,2
=
![]() .
В этом случае решение для переменных
представляет собой экспоненциально
затухающие гармонические колебания:
.
В этом случае решение для переменных
представляет собой экспоненциально
затухающие гармонические колебания:
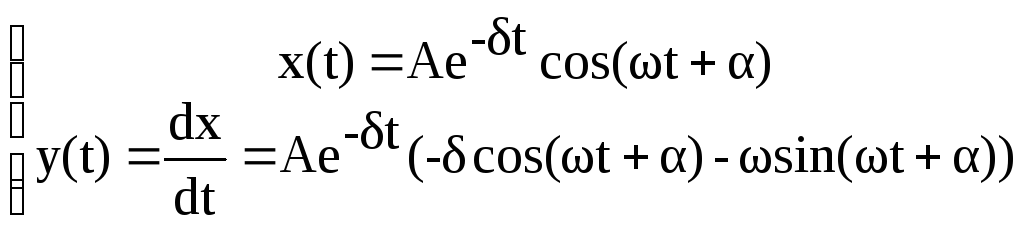 ,
тогда для случая ω » δ,
,
тогда для случая ω » δ,
 ,
вводя полярные координаты
,
вводя полярные координаты
![]() и вводя обозначение
и вводя обозначение![]() получаем уравнение траекторий колебаний
на фазовой плоскости в полярных
координатах ρ = ω А
получаем уравнение траекторий колебаний
на фазовой плоскости в полярных
координатах ρ = ω А![]() ,
т.е. накручивающуюся на особую точку
спираль.
,
т.е. накручивающуюся на особую точку
спираль.
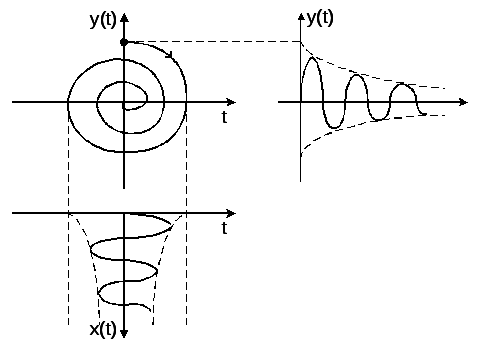
Особая точка – устойчивый фокус.
Рис. 3.
3).
а1 <
0; а2
> 0; а2
> (![]() )2.
Корни характеристического полинома
для этого случая равны:
)2.
Корни характеристического полинома
для этого случая равны:
p1,2
=
![]() .
В этом случае решение для переменных
представляет собой экспоненциально
нарастающие гармонические колебания:
.
В этом случае решение для переменных
представляет собой экспоненциально
нарастающие гармонические колебания:
 ,
тогда для случая ω » δ,
,
тогда для случая ω » δ,
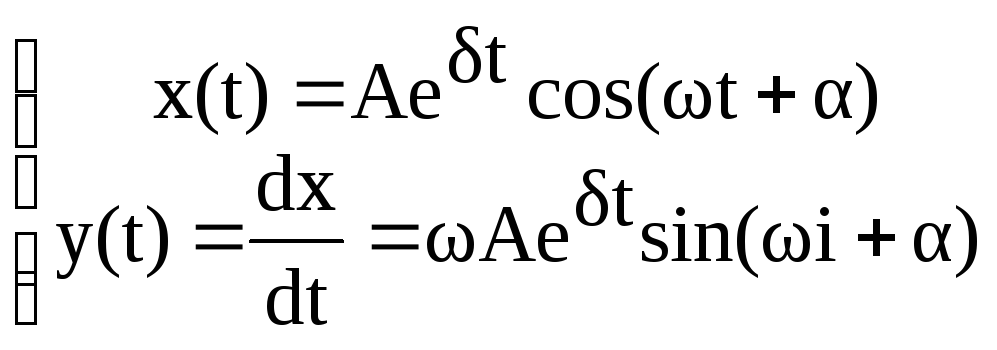 ,
вводя полярные координаты
,
вводя полярные координаты
![]() и вводя обозначение
и вводя обозначение![]() получаем уравнение траекторий колебаний
на фазовой плоскости в полярных
координатах ρ = ω А
получаем уравнение траекторий колебаний
на фазовой плоскости в полярных
координатах ρ = ω А![]() ,
т.е. раскручивающуюся от особой точки
спираль.
,
т.е. раскручивающуюся от особой точки
спираль.
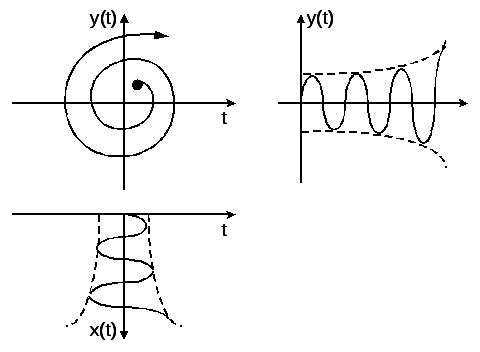
Особая точка – не устойчивый фокус.
Рис.4.
4).
а1<
0; а2
> 0; а2
> (![]() )2
. Корни характеристического полинома
для этого случая равны:
)2
. Корни характеристического полинома
для этого случая равны:
p1
= - δ1
и p2
= - δ2
. В этом случае решение для переменных
представляет собой экспоненциально
убывающие апериодические
колебания

1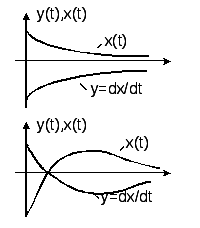 ).
).

1
1
Особая точка – устойчивый узел.
2).

2
Рис.6. Рис.5.
5).
а1 >
0; а2
> 0; а2
< (![]() )2
. Корни характеристического полинома
для этого случая равны:
)2
. Корни характеристического полинома
для этого случая равны:
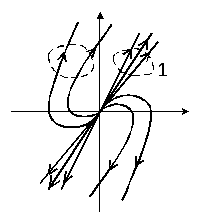
p1 = + δ1 и p2 = + δ2 . В этом случае решение для переменных представляет собой экспоненциально нарастающие апериодические колебания:

 y(t)
y(t)
2

 ).
1
2
).
1
2
 2
2
Особая точка – не устойчивый узел
x(t)
1).
Рис.8. Рис.7.
6 ).
а2
< 0, тогда p1
= + δ1
и p2
= - δ2
.
).
а2
< 0, тогда p1
= + δ1
и p2
= - δ2
.
 1
1
Особая точка – седло.
Прямые линии – называются сепаратриссами. Они
разделяют фазовую плоскость на области притяжения к двум устойчивым особым точкам 1 и 2.

2 Рис.9.
На плоскости значений коэффициентов а1 и а2, принадлежность особых точек, какому- то типу может быть представлена в виде следующего графика

Рис.10.
или таблицы:
|
а1
а2 |
а1 > 0 |
а1= 0 |
а1< 0 | ||
|
а2
< ( |
а2
> ( |
----
|
а2
< ( |
а2
> ( | |
|
уст. узел |
Уст. фокус |
центр |
не уст. узел |
не уст. фокус | |
|
а2 < 0 |
седло | ||||
Проиллюстрируем один из вариантов метода фазовой плоскости на примере анализа цепи с туннельным диодом.

Система уравнений имеет вид
![]()
![]()
![]()
![]() (для
контура 1)
(для
контура 1)
![]() (для
узла 1)
(для
узла 1)
Подставляя второе уравнение в первое получим
![]()
Аппроксимируем
φ(u)
рядом
![]()
Пусть
рабочая точка на характеристике выбрана
на середине падающего участка, а U0
–постоянная составляющая, соответствующая
выбранной рабочей точке. Обозначим
![]() -переменную
составляющую.
-переменную
составляющую.
Т огда
огда![]() .
Учитывая, что
.
Учитывая, что![]() и обозначая
и обозначая![]() запишем уравнение цепи в виде
запишем уравнение цепи в виде
![]()
Введем
безразмерное время τ:
![]() и приведём уравнение к виду
и приведём уравнение к виду![]()

![]()
Перейдём к уравнениям, позволяющим определить координаты особых точек. Обозначим
![]() ,
тогда из последнего уравнения
получаем:
,
тогда из последнего уравнения
получаем:

Делим второе уравнение на первое и тогда получим уравнение вида
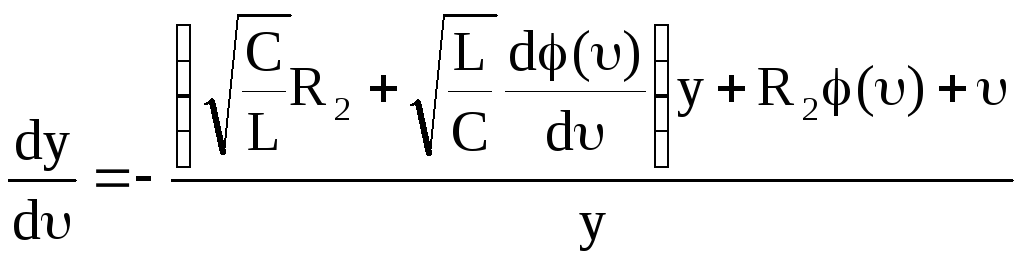
которое
описывает все интегральные кривые на
фазовой плоскости величин
![]() иy.
иy.
Особые точки на фазовой плоскости удовлетворяют уравнениям
![]() (т.е
все особые точки в рассматриваемом
случае располагаются на оси абсцисс
(т.е
все особые точки в рассматриваемом
случае располагаются на оси абсцисс
![]() )
)
![]() ,
,
откуда с учётом того, что y=0, получаем
![]() или
или
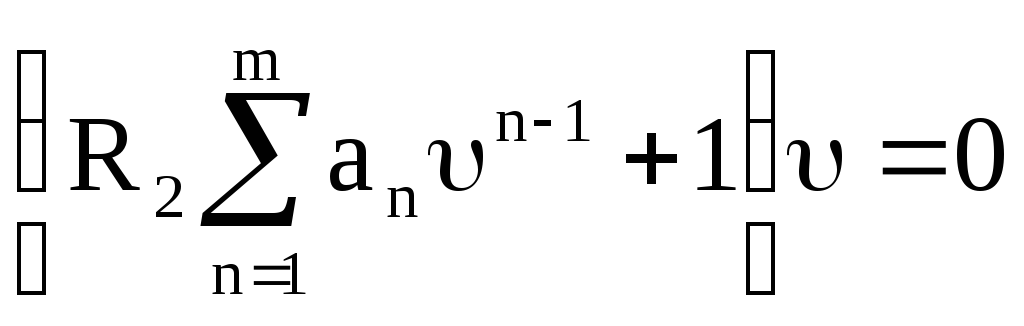
Т.е.
одна особая точка располагает в начале
системы координат y1=0;
![]() =0.
Для определения координат остальных
особых точек следует решить уравнение
вида
=0.
Для определения координат остальных
особых точек следует решить уравнение
вида![]()
Пусть,
например
![]() ,
,
тогда
![]() - (знакомый по предыдущим параграфам
вид аппроксимирующего полинома)
- (знакомый по предыдущим параграфам
вид аппроксимирующего полинома)
Следовательно, уравнение для координат особых точек примет вид
![]()
Откуда
находим, что
![]()
![]() ,
причём для существования этих особых
точек необходимо, чтобы
,
причём для существования этих особых
точек необходимо, чтобы![]() >0.
>0.
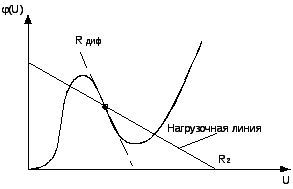
Фазовые
портреты для случая
![]() <0
и
<0
и
![]() >0
>0

Таким
образам на фазовой плоскости имеются
три особые точки. Первая с координатами
![]() существует при любых параметрах цепи,
вторая и третья с координатами
существует при любых параметрах цепи,
вторая и третья с координатами
 и
и существуют при условии, что
существуют при условии, что![]() >0,
т.е.R2
> R1диф.
>0,
т.е.R2
> R1диф.
На следующем этапе необходимо определить типы найденных особых точек.
Пренебрегая
слагаемыми 2ого
порядка малости
![]() в окрестности первой особой точки (в
окрестности 0) запишем уравнение ( ) в
виде
в окрестности первой особой точки (в
окрестности 0) запишем уравнение ( ) в
виде

Е сли
эта особая точка единственная, т.е.
сли
эта особая точка единственная, т.е.![]() <0,
тогда
<0,
тогда![]() >0
и точка является: либо центром
>0
и точка является: либо центром![]() ,
либо устойчивым фокусом или узлом (
,
либо устойчивым фокусом или узлом (![]() >
>![]() ),
либо неустойчивым фокусом или узлом(
),
либо неустойчивым фокусом или узлом(![]() <
<![]() ).
В последнем случае для неустойчивой
особой точки на фазовой плоскости обязан
существовать предельный цикл, поскольку
вследствие конечности энергии источника
).
В последнем случае для неустойчивой
особой точки на фазовой плоскости обязан
существовать предельный цикл, поскольку
вследствие конечности энергии источника![]() амплитуда
колебаний не может достигать бесконечно
больших значений.
амплитуда
колебаний не может достигать бесконечно
больших значений.
Фазовый портрет для этого случая представлен на рисунке. Именно этот случай рассматривался в предыдущих трёх параграфах. Причём раскачке колебаний соответствует область вблизи 0, установившимся колебаниям соответствует предельный цикл, который будет устойчивым.
Возвращаясь к исходному уравнению
![]()
Рассмотрим
интегральных кривых в окрестностях
![]() и
и![]() особых точек
особых точек
![]() ;
;
![]()
Положим
![]() и получим
и получим

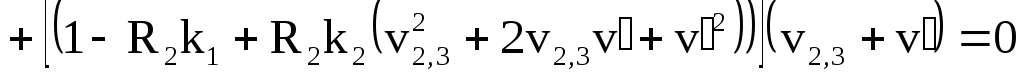
![]()
Учитывая,
что
![]() получаем
получаем
![]()
![]()
Замечаем
,что по условию существования корней
![]()
Следовательно
первая особая точка обязательно седло,
вторая и точки третья особые точки
обязательно не седла. При
![]() это устойчивый фокус или узел. Сепаратрисса,
порожденная седлом, разделяет фазовую
плоскость на 2 области притяжения к
устойчивым особым точкам 2 и 3.
это устойчивый фокус или узел. Сепаратрисса,
порожденная седлом, разделяет фазовую
плоскость на 2 области притяжения к
устойчивым особым точкам 2 и 3.
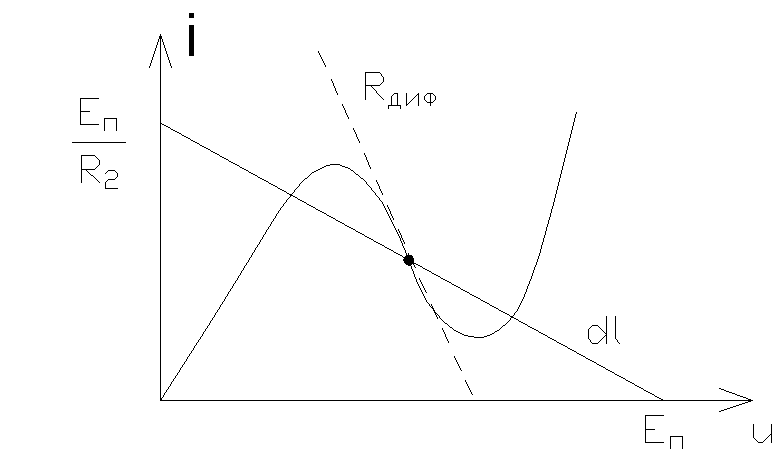
В
этих точках дифференциальное
сопротивление отрицательно и
следовательно
![]() может
быть < 0.
может
быть < 0.

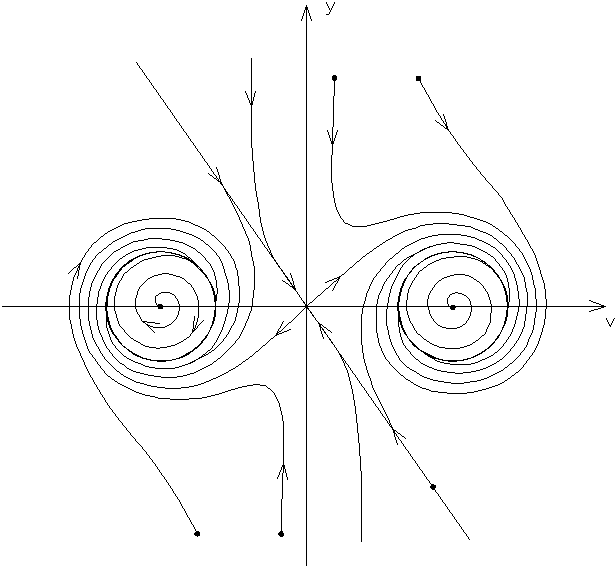
Сравним полученные результаты с результатами полученными ранее:
а)
В методе линеаризации мы получили, что
рабочая точка по постоянному току
устойчива когда
 .
Замечая ,что
.
Замечая ,что![]() ,
обнаруживаем совпадение критериев
устойчивости. Причем метод фазовой
плоскости указывает, что произойдет в
цепи при выполнение условия
,
обнаруживаем совпадение критериев
устойчивости. Причем метод фазовой
плоскости указывает, что произойдет в
цепи при выполнение условия
б)
В методе линеаризации было получено
условие устойчивости колебаний в
окрестности устойчивой рабочей точки
![]() >
>![]() .
В методе фазовой плоскости с учётом
.
В методе фазовой плоскости с учётом![]() ,
условие устойчивости
,
условие устойчивости![]() >
>![]() ,
совпадает с
,
совпадает с![]() >
>![]() .
.
в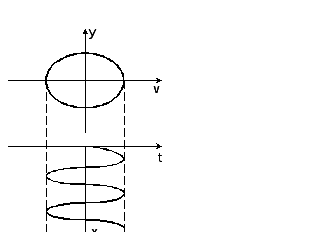 )
Методом гармонической линеаризации
были рассмотрены стационарные колебания
(для случая
)
Методом гармонической линеаризации
были рассмотрены стационарные колебания
(для случая![]() ).
На фазовой плоскости этим колебаниям
соответствует предельный цикл.
).
На фазовой плоскости этим колебаниям
соответствует предельный цикл.
г) Метод медленно меняющихся амплитуд позволил получить решение, включавшее в себя результаты как МЛ так и МГЛ внутри цикла.