Колебания и волны.

Введение.

Вряд ли есть необходимость специально обосновывать важное значение колебательных процессов в современной физики и технике. Можно без преувеличения сказать, что почти нет области в этих науках, в которой колебания не играли бы той или иной роли, не говоря уже о том, что ряд областей физики и техники всецело базируются на колебательных явлениях. Достаточно, например, указать область электромагнитных колебаний, включающую в себя и оптику, на учение о звуке, на радиотехнику и прикладную акустику, вибрации машин, автоколебания в системах регулирования и следящих системах. Все эти, казалось бы, различные и непохожие друг на друга колебательные процессы объединяются методами математической физики в одно общее учение о колебаниях.

Общность колебательных процессов, их разнообразие и в тоже время их специфическое своеобразие, играют существенную роль в установлении внутренних связей между весьма разнообразными, на первый взгляд, явлениями. Этим обстоятельством, как мне кажется, и обусловливается, главным образом, принципиальное значение и важность интересующей нас области.

Весьма существенно следующее: в области колебаний особенно объективно выступает взаимодействие между физикой и математикой, влияние потребностей физики на развитие математических методов и обратное влияние математики на физические знания.

В качестве оного из примеров можно взять машиностроение. Еще не так давно изучение колебаний здесь не придавалось особого значения, и расчеты на прочность велись на основе статических представлений о зависимости деформаций от нагрузок. Однако вместе со стремлением к увеличению числа оборотов и уменьшению габаритов при переходе к скоростному машиностроению пренебрегать ролью колебаний стало уже невозможно. Многочисленные аварии, связанные с увеличением фактических нагрузок из-за возбуждения колебаний, сделали необходимым для конструкторов и инженеров тщательное исследование возможных вибраций узлов машин и оценку их интенсивности. С развитием физики и математики большую роль теория колебаний сыграла в авиации (эффекты шимми), космонавтики и т.д.

Истоки современного учения о колебаниях мы можем заметить в классической механике времен Галилея, Гюйгенса, Ньютона в задачах о движении маятника. В трудах Лагранжа имеется уже сформировавшаяся теория малых колебаний. При дальнейшем развитии она получила название теории линейных колебаний, т.е. колебаний, характеризуемых линейными дифференциальными уравнениями с постоянными коэффициентами как однородных, так и со свободными членами, являющимися известными функциями времени.

В трудах ряда ученых линейные дифференциальные уравнения стали мощным орудием исследования. Так А.М. Крылов и его ученики, развивавшие теорию линейных колебаний, с успехом применяли ее к проблемам о качке корабля, к теории гироскопа, к задачам артиллерии.

Простота основных принципов, теории линейных дифференциальных уравнений с постоянными коэффициентами обусловила большую разработанность теории линейных колебаний, общность формулировок ее законов и их физическую наглядность. Свойство линейности дифференциальных операторов, интерпретируемое как принцип суперпозиции колебаний, позволили сводить исследование влияния произвольных приложенных сил на линейную колебательную систему к исследованию влияния сил простейшего типа, гармонически зависящих от времени. Тем самым выработался «спектральный» подход к колебательным процессам, получившим громадное значение и вне теории колебаний в собственном смысле.

Лишь после 20-х годов настоящего столетия, после работ Карсона, Дейча, Бромвича и др., математическая сторона символического метода начала существенно проясняться, связываясь с преобразованием Лапласа и мощными методами теории функций комплексного переменного. Вопросам теории и приложения символических методов в настоящее время посвящена обширная литература

Ввиду того, что теория линейных колебаний по указанным выше причинам разработана весьма детально, и ее математический аппарат действует, можно сказать почти автоматически, исследователи стремились изучаемые ими колебания подводить под линейные схемы, отбрасывая часто без должного обоснования нелинейные члены. При этом иногда совершенно упускалось из виду, что такая «линейная» трактовка может привести к существенным ошибкам не толь количественного, но и принципиально качественного характера.

Наш курс будет ориентирован на исследование колебательных процессов в различных радиотехнических системах. В прошлых семестрах вы изучали в основном линейные инвариантные системы, линейные системы с распределенными элементами и в меньшей степени нелинейные системы. На самом деле все процессы, происходящие в природе, если подходить более строго к моделям описывающих их, относятся к нелинейным процессам. Только лишь нелинейные системы позволяют получить все интересные устройства в радиотехнике, такие как детекторы, модуляторы, генераторы, пере множители, стабилизаторы и многие другие. Поэтому в курсе, который вы будете изучать, в этом семестре будут, представлены методы позволяющие, проанализировать процессы, происходящие в таких системах.

Классификация колебательных систем.

В соответствии, с изложенным выше все колебательные системы можно делить на линейные, параметрические и нелинейные.

Линейные цели описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Для линейных систем выполняется принцип суперпозиции, т.е. отклик системы на сложное воздействие, равняется сумме откликов на каждое воздействие в отдельности. В линейных инвариантных цепях происходит лишь деформация спектра, т.е. спектральные составляющие входного сигнала изменяют лишь свою амплитуду и новых спектральных составляющих не возникает.

Параметрические системы описываются линейными дифференциальными уравнениями с переменными коэффициентами, т.е. коэффициентами, зависящими от аргумента (времени).

Нелинейные системы описываются нелинейными дифференциальными уравнениями, т.е. уравнениями с коэффициентами, зависящими от функции (тока, напряжения). Для нелинейных систем принцип суперпозиции не выполняется. В параметрических и нелинейных системах происходит деформация спектра входного сигнала.

Кроме такой классификации колебательные системы можно разделить на дискретные (с сосредоточенными параметрами) и сплошные (с распределенными параметрами).

Дальнейшая классификация может идти по числу степеней свободы или по порядку степени дифференциального уравнения, описывающего систему. Известно, что формально число степеней свободы колебательной системы равно половине порядка ее дифференциального уравнения. Поэтому дискретные системы можно классифицировать на системы с нулевой, полу целой, одной и т.д. степенями свободы (из механики известно, что количество степеней свободы – это количество независимых переменных необходимых для полного описания движения системы).

Кроме того, колебательные системы могут быть консервативными и неконсервативными; автономными и неавтономными и т.д.

Глава 1.

Свободные и вынужденные колебания в линейных инвариантных динамических системах.

§1.1.Преобразование Лапласа и его основные свойства.

В технических науках, в особенности в теории линейных электрических цепей, технической кибернетики и др., широко используется преобразование Лапласа. Это интегральное преобразование, которое определенным функциям f(t) действительного переменного t, называемым оригиналами, по формуле

F(p)= (1.1)

ставит в соответствие функции F(p) комплексного переменного p=δ+iω называемые изображениями. Для связи f(t) и F(p) вместо (1.1) используют различные обозначения, в том числе F(p)=[f(t)] или f(t) F(p), где - оператор прямого преобразования Лапласа.

Обычно к классу функций – оригиналов относят «классические» функции ограниченного роста, удовлетворяющие условиям Дирихле и отличные от нуля при t≥0. Однако для ряда важных приложений удобно класс оригиналов расширить, включив в него обобщенные функции – импульсную функцию Дирака δ(t) и ее производные. Правомерность такого расширения обоснована в теории обобщенных функций.

Найдем изображение некоторых важных для практики функций:

а) Изображение единичной ступенчатой функции

σ(t)═{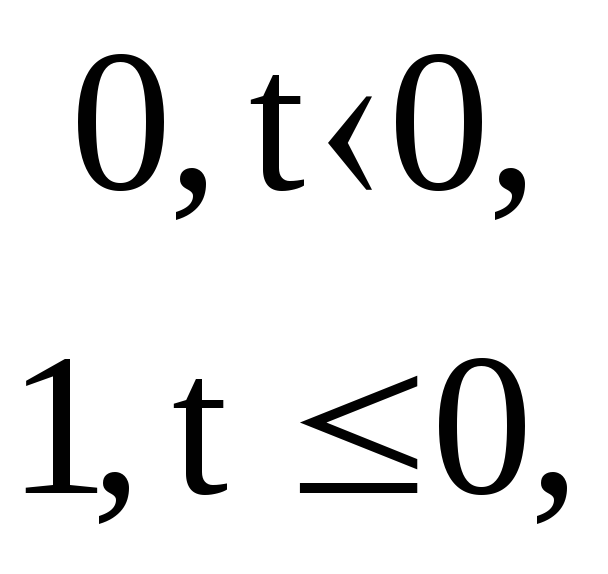 [σ(t)]==. (1.2)

б) Изображение экспоненциальной функции

f(t)={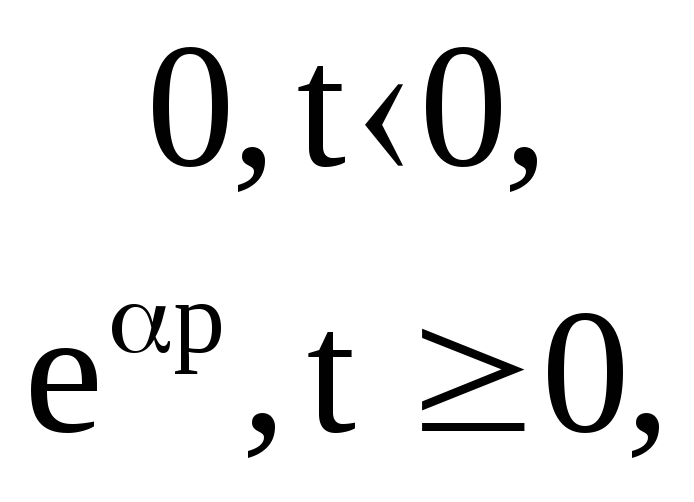 = e F(p)= =. (1.3)

в) Изображение импульсной функции Дирака

[δ(t)== e^-p0 = 1. (1.4)

Следующие свойства преобразования Лапласа являются основными для его широкой применимости. Они соответствуют операциям, которые выполняются над функциями-оригиналами, причем каждый раз функция, являющаяся результатом той или иной операции, должна принадлежать к классу функций – оригиналов. Во всех свойствах F(p) – изображение исходной функции – оригинала, подвергаемой операциям.

1. Линейность преобразования:

[] =. (1.5)

2. Изображение производной:

[] =pⁿ. (1.6)

3. Изображение интеграла:

[]=. (1.7)

4. Изображение функции с запаздывающим аргументом:

[f(t-θ)] = e^-pF(p) (1.8)

5. Изображение функции с экспоненциальным сомножителем:

[f(t)e^at]=F(p-a). (1.9)

5. Изображение свертки функций:

[dτ]=F₁(p)F₂(p). (1.10)

7. Изображение функции с измененным масштабом:

[f(аt)]=F(). (1.11)

8. Изображение функции с сомножителем tⁿ:

[tⁿ f(t)]=(-1)ⁿ F⁽ⁿ⁾(p). (1.12)

8. Изображение функции с сомножителем :

[f(t)]=. (1.13)

8. Изображение произведения функций:

[f₁(t)f(t)]= (1.14)

Зачастую изображения можно находить без сложного вычисления интеграла Лапласа, а лишь путем использования перечисленных свойств.

Пример: а) Изображение косинусоидальной функции:

Acosω₀tσ(t)=½A(e^iωt + e^-iωt)½A()=.(1.15)

б) Изображение прямоугольного импульса:

П(t)=A[σ(t) - σ(t-θ)] (1 - e^{-p θ)}. (1.16)

в) Изображение косинусоидальной функции с изменяющейся амплитудой:

σ(t)A(t)cosωt=½A(t)(e^iωt + e^-iωt)σ(t)½[A(p-iω) + A(p+iω)]. (1.17)

Обратное преобразование Лапласа, однозначно восстанавливающее оригинал по своему изображению, определяется интегралом:

f(t)= [F(p)]= (1.18)

Особую значимость для приложений имеет обратное преобразование дробно-рациональных функций F(p)=. Такую функцию достаточно разложить на элементарные дроби и, воспользовавшись свойством линейности ограничиться преобразованием дробей

F(p)=(t≥0). (1.19)