§2.4.2 Метод последовательных приближений.
В
системе могут рассматриваться как
свободные, так и вынужденные колебания.
Пусть колебания параметров происходят значительно медленнее по сравнению с характерными колебаниями напряжения или тока.
Этот метод позволяет получить ряд последовательных поправок к методу замороженного параметра.
Пусть у нас система с сосредоточенными параметрами (радиотехническая цепь).
.
Пусть
можно представить матрицу
в виде постоянной величины и медленно
изменяющейся вокруг нее переменной
части.
Тогда
-
будем считать, что это известная функция
времени.
Осуществим преобразование Лапласа.
Решение будем искать в виде
,
тогда
На первом этапе пренебрегаем последним слагаемым.
,
после чего находим:
-
эти найденные контурные токи подставим
в
и получим известный столбец функций.
Осуществим обратное преобразование
Лапласа. Подставим это в
.
И найдем, теперь первую поправку.
………
§2.4.2. Метод последовательных приближений (второй вариант).
Применяется
при медленном изменении параметров по
сравнению с характерным периодом. Как
предыдущий этот период основан на
преодр.
Система
уравнений цепи
Пусть
;
;
Тогда
еще
ничего не изменилось.
Обозначим
- и рассматриваем
как известные функции, тогда после
применения преобразования Лапласа
имеем
-
система алгебраических уравнений.
Решения
этой
системы
,
где
Ищем
в виде ряда
где
,
(
=
(
)
- решения, совпадающее с решением методом
«замороженного» параметра.
Эти
решения подставляем после
в
уравнения
и находим 2е
слагаемое
ряда
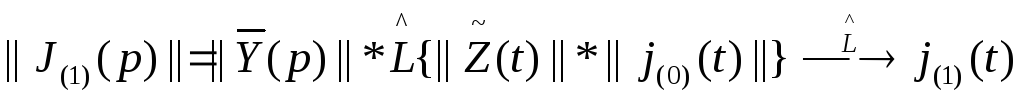и
т. д.
. . . . . . . . . . . . .
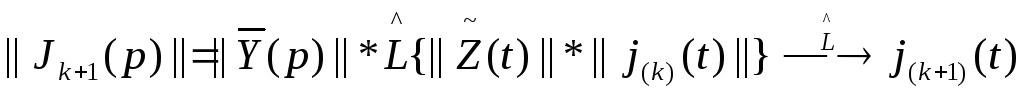
Правомерность
разложения, примененного в этом методе,
доказывается путем перехода к интегральным
уравнениям и использованием свойств
последних. Наконец
§2.4.3 Метод вкб.
Этот
прием связан с решение дифференциальных
уравнений вида
(илиS(t)).
Решение ищется в виде
-
связана со скоростью изменения функции
на первом этапе малой величины
теперь
продифференцируем это еще раз и подставим
в добавку.
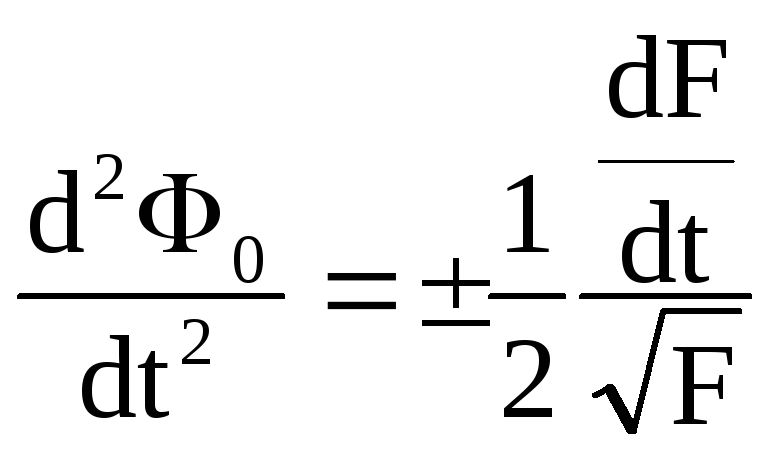
Если
окажется, что
,
то можно ограничится этим шагом.
Теперь
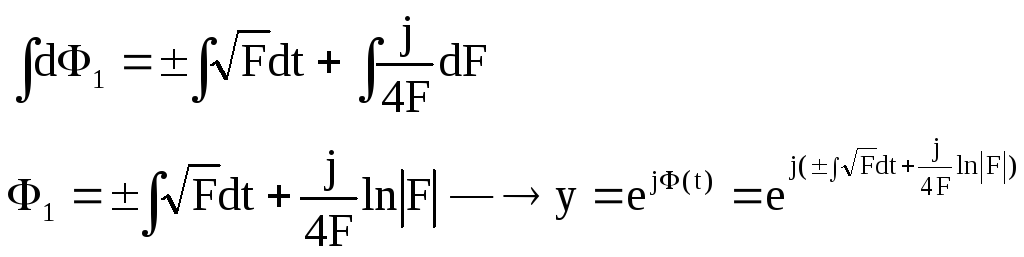
§2.4.3. Метод вкб (Вентцеля-Крамерса-Бриллюэна)(второй вариант).
Метод,
предназначен для нахождения приближенных
решений уравнений вида:
-
уравнение Хилла, причем на функциюF(t)
накладывается ряд ограничений.
При определенном подходе к анализу параметрических цепей, последние в ряде случаев, могут быть представлены соединением простых цепей, каждая из которых описывается дифференциальными уравнениями порядка не выше 2го.
В общем случае такой цепью является одноконтурная цепь, содержащая все элементы с переменными характеристиками. Уравнение цепи запишем в виде
,
где
или
,
где
Используем
замену 
,
находим первую и вторую производные
для q(t)
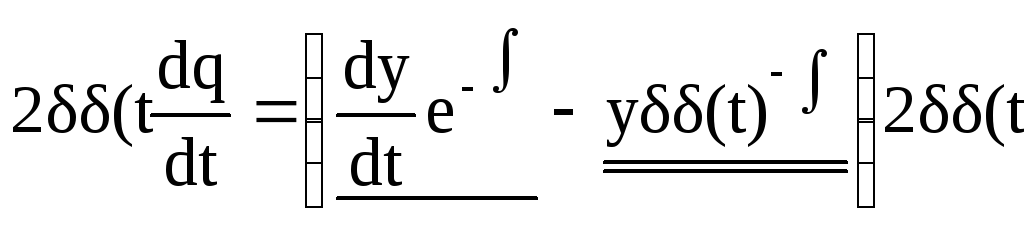
После подстановки получим
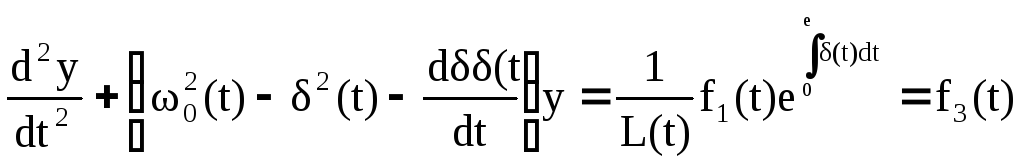
Решение
неопределенного уравнения Хилла
,
находится с помощью, метода вариации
постоянной составляющей решения
однородного уравнения Хилла
.
Найдем с помощью метода ВКБ решение однородного уравнения Хилла.
Для
того чтобы возможно было применить
метод ВКБ, функция F(t)
должна удовлетворять следующему условию
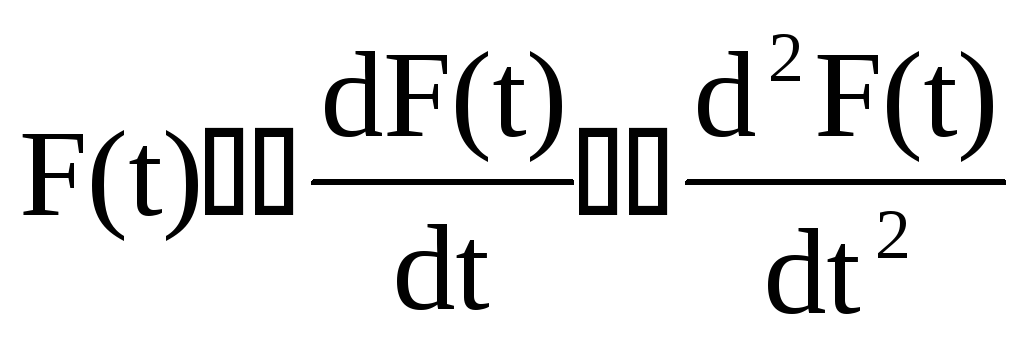(медленное изменениеF(t))
Пусть
,
т.у.F(t)>0
(это требование не обязательно в методе
ВКБ).
Ищем
решение однородного уравнения Хилла в
виде следующей функции
.
Тогда
.
Поэтому :
Полученное
уравнение является неоднородным, решить
которое труднее чем исходное. Однако,
если
мало, можно использовать метод итераций
.
Пусть
Тогда
нулевое приближение находим из уравнения
.
Условие
применимости нулевого приближения
Подставим Ф0 в правую часть уравнения.
,
(использовано разложение в ряд Тейлора
)
Откуда получаем 1е приближение
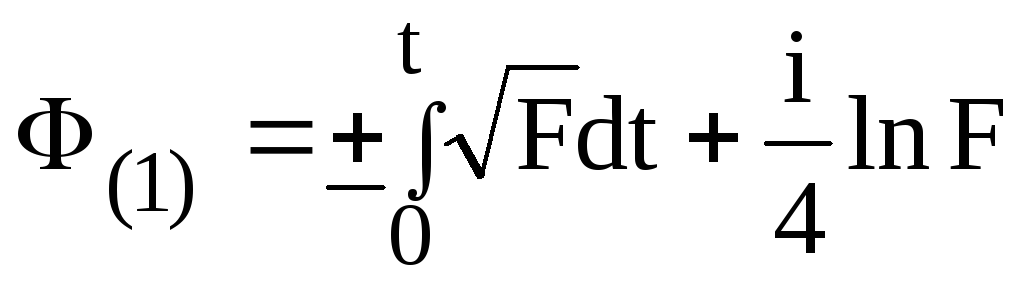
Процесс
итерации можно продолжить
,
но мы ограничимся
первым приближением. Как видно решением уравнения Хилла являются две функции
,
.
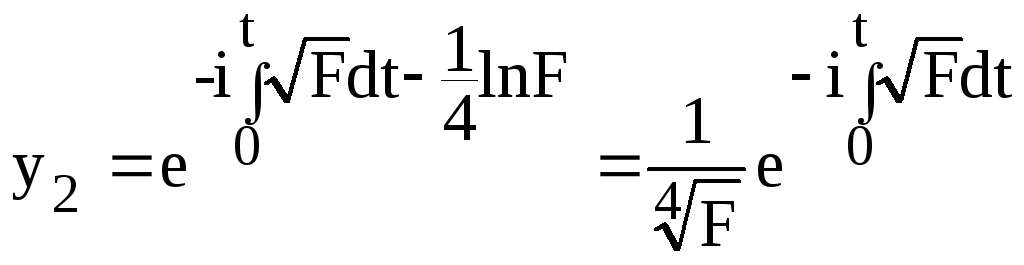Следовательно, решением уравнения Хилла будет сумма: y(t)=U1y1(t) + U2y2(t).
Решение неоднородного уравнения
можно
находить методом вариации произвольных
постоянных. Поэтому решение ищем в виде
,
где
и
- некоторые неизвестные коэффициенты.
Найдем 1ю
производную
.
При
произволе выбора коэффициентов потребуем,
что бы
,
тогда вторая производная:
.
Подставим найденные первую и вторую
производные в уравнение.
Таким
образом, имеем систему уравнений
относительно
откуда
находим
Пусть
,
тогда
,
тогдаu1
и u2
а
следовательно
,
возвращаясь к
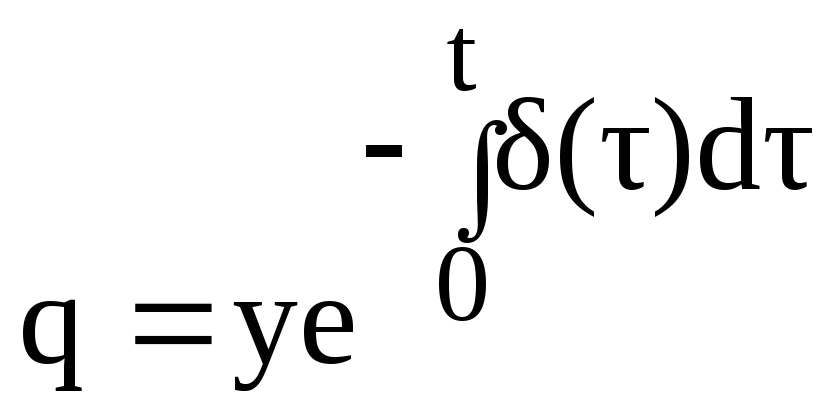
Напомним,
что
,
тогда переход к постоянным значениям
дает следующий результат:
,
а