§3.2. Метод гармонической линеаризации (мгл).

Метод МГЛ применим для исследования, как свободных, так и вынужденных колебаний в нелинейных цепях (системах).

S

нел. цепь

_вхcosω₀t S_выхcosω₀t или S_выхcosnω₀t

Идея метода: если за счет фильтрующих свойств нелинейной системы, колебания в ней близки к гармоническим, то нелинейные элементы в такой системе можно заменить эквивалентными линейными элементами, с параметрами соответствующими данному режиму гармонических колебаний. Метод применим для исследования стационарных процессов близких к гармоническим в нелинейных системах с ярко выраженными резонансными свойствами. После замены нелинейных элементов линейными колебания в цепи могут исследоваться любым из методов линейной теории.

§3.2.1. Эквивалентные параметры нелинейных элементов.

Рассмотрим нелинейный элемент – нелинейное сопротивление. Ток задан ВАХ нелинейного элемента. Пусть напряжение является гармоническим (в силу резонансных свойств внешней к нелинейному сопротивлению цепи).

G_экв

i = φ(u) i(t)

u(t) = Ucosω₀t u(t) = Ucosω₀t

i(t) = φ(Ucosω₀t) = cosnω₀t; i(t) = G_эквUcosω₀t;

где ;

Если нелинейная система включает в себя резонансный контур, то за счет резонансных свойств контура из всех гармоник существенными будет лишь составляющая основной частоты ω₀. Следовательно, ток i в нелинейном контуре есть

i(t) = (.

Сравнивнивая токи в нелинейном и эквивалентном ему линейном контурах получаем, что

G_экв = .

Аналогичным образом можно найти параметры С_экв, L_экв, R_экв:

R_экв = ;

C_экв = ;

L_экв = .

В выражения для эквивалентных параметров входят ВАХ нелинейных элементов. Определим эквивалентные параметры в двух случаях: полиномиальной и кусочно-линейной апраксимаций.

Полиномиальная аппроксимация.

В случае полиномиальной аппроксимации ВАХ нелинейных элементов могут быть представлены в виде

φ(U) = a₀ + a₁U + a₂U² + a₃U³ + …

Так как закон изменения напряжения у нас гармонический, то u(t)=Ucosω₀t и, следовательно

φ(Ucosω₀t) = a₀ + a₁Ucosω₀t + a₂U²cos²ω₀t + a₃U³cos³ω₀t + … = (a₀ + a₂ + …) + (a₁U +

+ a₃U³ + a₅U⁵ + …)cosω₀t + ( a₂U² + … )cos2ω₀t + …

Подставляя найденное выражение для ВАХ в выражение для G_экв получим

G_экв = a₁ + a₃U² + a₅U⁴ + …

Аналогично находим эквивалентные параметры нелинейных элементов в случае ампер-веберной и вольт-кулоновской характеристик. Выражение для любого эквивалентного элемента имеет вид

П_экв = a₁ + a₃A² + a₅A⁴ + … , где А – это амплитуда напряжения U для G_экв, C_экв и амплитуда тока I для R_экв , L_экв соответственно.

При кусочно-линейной аппроксимации вида

i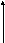(t)

i(t) =

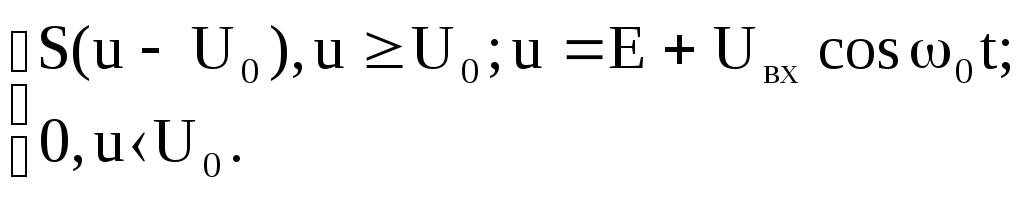
0 U₀ u(t)

С учетом того, что угол отсечки определяется выражением cosθ = , находим

i(t) =

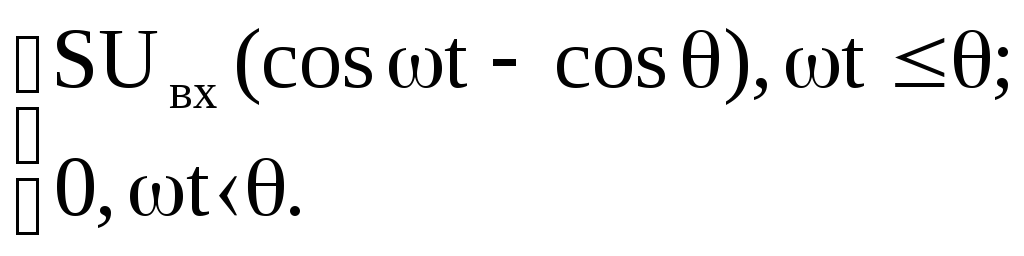
Тогда, с учетом того, что воздействие есть гармоническая функция, раскладываем ток в ряд Фурье

i(t) = , где I_n = SU_вх γ(θ), причем γ(θ) = - гамма функция, а θ = arccos.

Для иллюстрации МГЛ рассмотрим следующие упражнение.

Упр.1. Рассмотреть автоколебания в автогенераторе в схеме на туннельном диоде, определить амплитуду установившихся (стационарных) колебаний. Определить устойчивость автоколебаний.

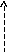
i L R₂ i(t) ξ

φ(t)

C U E_п v

U

Представим аппроксимацию ВАХ туннельного диода с помощью полиномиальной аппроксимации. В координатах связанных с точкой покоя ВАХ туннельного диода имеет вид

ξ

ξ = - k₁v + k₂v³, где k₁ и k₂ > 0.

Т.к. нелинейный элемент – туннельный диод подключен к внешней по отношению к нему резонансной цепи, то такой нелинейный элемент может быть заменен эквивалентной ему линейной проводимостью G_экв. Эквивалентная схема такого генератора для режима колебаний имеет вид

Тогда характеристический полином имеет вид

G_экв С L V(p) = p² + ()p + (1 + R₂G_экв) = p² + a₁p + a₂ .

C учетом представленной аппроксимации ВАХ нелинейного элемента полиномом третьей степени G_экв имеет вид

G_экв = - k₁ + k₂ U².

Корни характеристического уравнения имеют вид p_1,2 = -, причем для генератора гармонических колебаний (и корни имеют вид p_1,2 = -δ ± jω₁. Подставим выражение G_экв в выражение для коэффициента а₁, получим а₁ = . Поэтому т.к. коэффициентa₁= а₁(U) является функцией амплитуды U, то условием определения стационарной амплитуды гармонических колебаний есть равенство а₁(U_ст) = 0. Откуда находим, что

+ =0.

U_ст = .

Как уже отмечалось в методе линеаризации, для гарантированного получения генератора гармонических колебаний необходимо, чтобы R₂ = 0, следовательно

U_ст = .

Таким образом, стационарные колебания в автогенераторе гармонических колебаний имеют следующий вид

u(t) = U_стcos(ω₀t + φ) = 2cos(.

Стационарные колебания (найденные выше) являются устойчивыми. Для вывода условия устойчивости стационарных колебаний воспользуемся следующими рассуждениями. Если стационарные колебания устойчивы, то при отклонении амплитуды колебаний от стационарной, условие равенства коэффициента а₁(U) нулю не будет выполняться. Причем если (U_ст +∆U), то действительная часть корней характеристического полинома должна быть

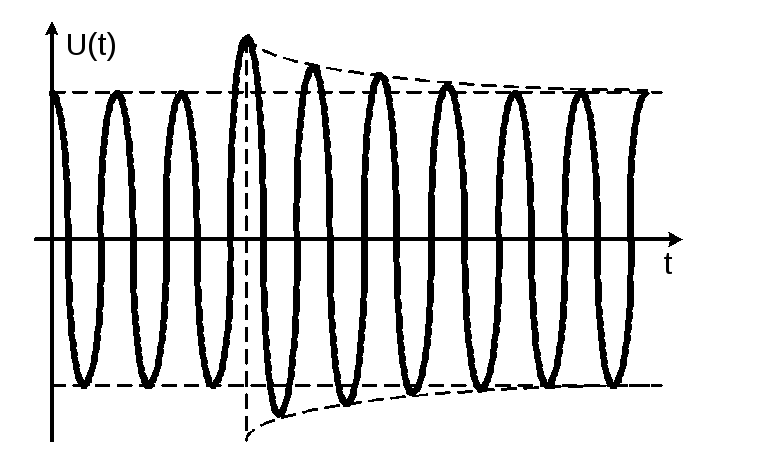
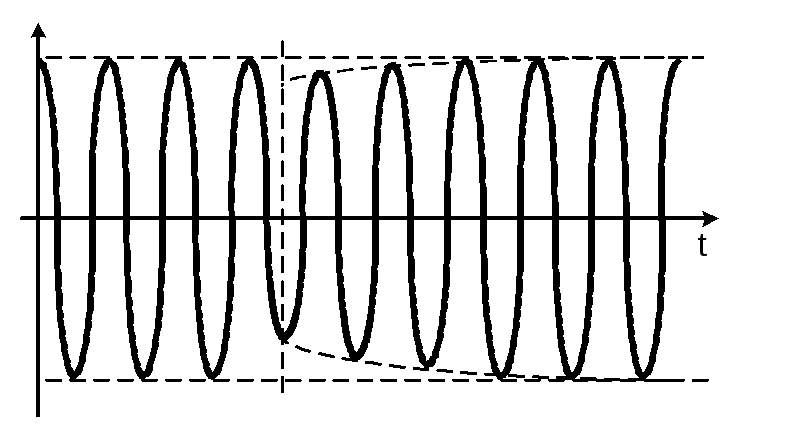
положительной, чтобы решение S_вых = S₀ e^-δtcos(ω₁t + φ) стремилось вернуться к стационарному решению. А при (U_ст - ∆U) действительная часть корней характеристического полинома должна быть отрицательной, чтобы решение S_вых нарастало и стремилось вернуться к стационарному решению. Таким образом, условием устойчивости стационарной амплитуды гармонических колебаний есть условие

а₁(U ± ∆U) = ±A∆U, где коэффициент А>0.

Проверим устойчивость стационарной амплитуды гармонических колебаний

δ(U_ст + ∆U) = =

= =A∆U +;

т.к. отклонения ∆U от стационарной амплитуды колебаний есть малая величина, то вторым слагаемым можно пренебречь. Т.о. стационарные колебаний в автогенераторе на туннельном диоде, являются устойчивыми.

График зависимости G_экв (U) представлен на рис. Значение U соответствующее G_экв=0 есть U_{ст .}

Итак в автооператоре на туннельном диоде состояние, когда колебания отсутствуют, является неустойчивым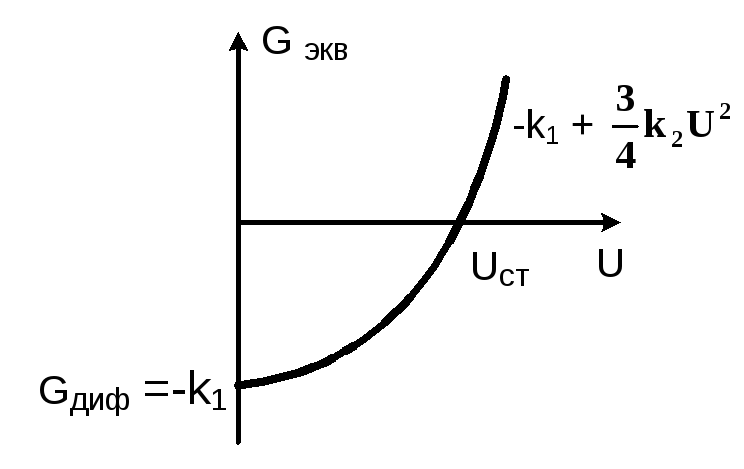

Малейшая флуктуация обуславливает возрастание амплитуды колебаний. При этом пока колебания малы, их амплитуда возрастает пропорционально . По мере

увеличения интервала t от момента возникновения колебаний амплитуда колебаний увеличивается, стремясь в пределе и величине U_ст. В цепи устанавливается режим автоколебаний.