§3.2.Особенности задач анализа колебаний в нелинейных цепях.

Анализ колебаний в нелинейных цепях представляет большие трудности. В настоящее время не существует единого математического метода, пригодного для исследования любых нелинейных цепей при произвольных режимах их работы. Каждый метод оказывается достаточно эффективным обычно лишь для одного или нескольких режимов работы того или иного класса нелинейных цепей.

В нелинейной цепи по сравнению с линейной возможен дополнительный режим – автоколебания. Поэтому при анализе могут исследоваться: устойчивость цепи ( ее состояние покоя ), устойчивость автоколебаний, установившейся режим автоколебаний, процесс установления автоколебаний, процесс исчезновения автоколебаний, преобразование автоколебания в устойчивой нелинейной цепи, взаимодействие внешнего колебания с автоколебанием в нелинейной цепи и другие.

Разновидности применяемых нелинейных цепей: - автогенераторы специальной и синусоидальной формы - умножители и делители частоты, т.е. преобразователи частот - ограничители

- выпрямители - модуляторы и демодуляторы - электронные реле.

Порядок дифференциального уравнения, описывающего колебания в нелинейной цепи, может быть различным до n=1020 и более. Соответственно многообразию видов нелинейных цепей, режимов их работы и поставленной задачи анализа в настоящее время известно несколько сотен различных методов исследования. Наиболее распространенные:

1. метод линеаризации

2. метод гармоничной линеаризации

3. методы малого параметра

4. метод усреднения

5. метод фазовой плоскости

6. метод интегральной аппроксимации

7. метод математического моделирования.

§3.3. Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений.

Рассмотрим нелинейную электрическую цепь, составленную частично или полностью из элементов активного сопротивления, каждый их которых определен своими характеристикамиU = f_k(i) и i = φ_k(u). Рассмотрим одномерную задачу анализа. Используем для анализа метод трансформации. φ_рез(u)

а)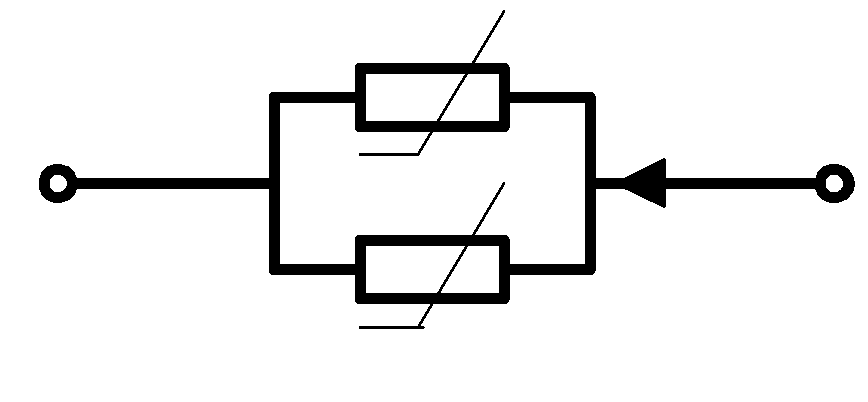

φ₁(u)

φ₂(u)

i = i₁+i₂ = φ₁(u)+φ₂(u) = φ_рез

б)

u = u₁+u₂ = f₁(i)+f₂(i) = f _рез(i)

Первый этап: цепь сводится к одному нелинейному элементу и при этом определяется напряжение или ток в цепи.

Второй этап: цепь разворачивается до искомого колебания.

Пример: 1^й этап

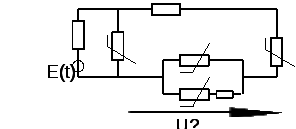
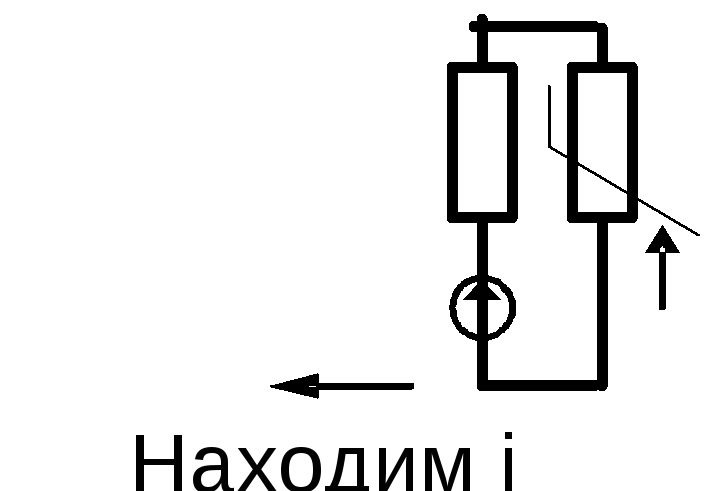
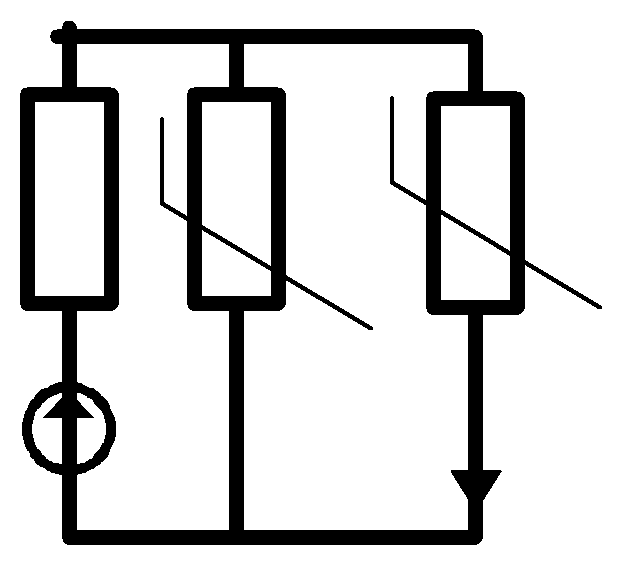
В нелинейной цепи, составленной из элементов R, происходит изменение спектра выходного колебания по сравнению со спектром входного колебания.

§3.4. Метод линеаризации.

Метод основан на предположении, что колебания, возбужденные в цепи, содержащей нелинейные элементы, являются настолько малыми, что участки характеристик нелинейных элементов, в пределах которых существуют колебания, могут считаться линейными.

Метод используется:

1. для анализа малых вынужденных колебаний в устойчивых цепях с нелинейными элементами.

2. для исследования устойчивости цепи при малых отклонениях от состояния покоя.

3. для исследования устойчивости периодического автоколебания.

Метод линеаризации использовался ранее при выводе схем замещения электронных приборов. Причем, параметры электронных ламп S = и , а также параметры транзисторов g_вх, g_обр, g_i и S – являются дифференциальными параметрами, определенными для некоторой окрестности рабочей точки (рекомендованной). Как следствие этого обстоятельства, анализ всех схем, содержащих электронные приборы ( усилители разнообразного назначения ), был проведен ранее именно методом линеаризации.

Алгоритм метода линеаризации для анализа вынужденных колебаний.

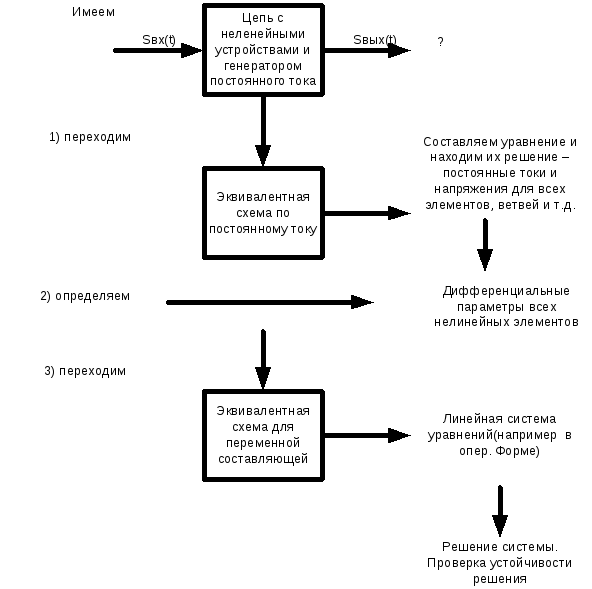
Рассмотрим применение этого метода для исследования устойчивости цепи при малых отклонениях от состояния покоя.

Цепь с нелинейным элементом и генератором постоянного тока

Пусть некоторая цепь содержит нелинейные устройства, а также генераторы энергии в виде источников постоянного напряжения или тока. Если колебания в цепи отсутствуют, то ее состояние покоя характеризуется постоянными значениями токовI₀ и напряжений U₀ ветвей, которые могут быть определены анализом режима постоянного тока. Постоянные значения токов и напряжений нелинейных элементов определяют положения рабочих точек на их характеристиках.

При возбуждении каким-либо образом цепи, колебаниями реакции будут отклонения ∆ U и ∆ i токов и напряжений от постоянных значений. Для анализа этих колебаний от схемы цепи переходят к схеме замещения для режима колебаний, причем нелинейные элементы заменяют линейными с параметрами, равными дифференциальными параметрам в определенной рабочей точке. Составляют систему уравнений для отклонений (колебаний). В операторной форме система имеет вид:

или

(справа в системе уравнений могут быть записаны изображения характеристических источников колебаний).

Характер колебаний в цепи определяется расположением корней характеристического уравнения

или pⁿ+a₁p^n-1+a₂p^n-2+…+a_n=0. Если все корни характеристического уравнения имеют отрицательные вещественные части ( т.е. если они лежат в левой полуплоскости ), тогда цепь является устойчивой. Свободные колебания в этом случае носят затухающий характер.

Если какие-либо корни характеристического уравнения имеют положительные вещественные числа, тогда в решении им будут соответствовать слагаемые вида:

S_eи S_ncos(ω_nt+ψ_n),

которые являются расходящимися. Такая цепь является неустойчивой.

Если характеристическое уравнение имеет порядок выше третьего, то корни не имеют аналитических выражений, связывающих их с коэффициентами a_k. Для анализа устойчивости следует либо вычислить корни уравнения каким-либо численным методом, либо использовать одни из критериев устойчивости, определяющих требование, которым должны удовлетворять коэффициенты a_k, для устойчивых цепей. Наиболее широкое распространение получили критерии Рауса – Гурвица, Михайлова и Найквиста.

Критерий устойчивости Рауса – Гурвица является аналитическим. Критерий Михайлова и Найквиста – графоаналитические.

Критерий Рауса-Гурвица предполагает рассмотрение главного определителя вида

D_{n =}

Из этого определителя выделяются:

1^й определитель D₁=a₁; 2^й определитель ; 3^й определитель

D₃= и т.д. Критерий Рауса – Гурвица устанавливает, что при a₀ > 0 все корни характеристического уравнения имеют положительные вещественные части, если все n определителя положительны.

Для иллюстрации метода линеаризации и критерия Рауса – Гурвица рассмотрим схему с туннельным диодом, способную при определенных условиях усиливать или генерировать колебания.

Моделирующая схема туннельного диода.

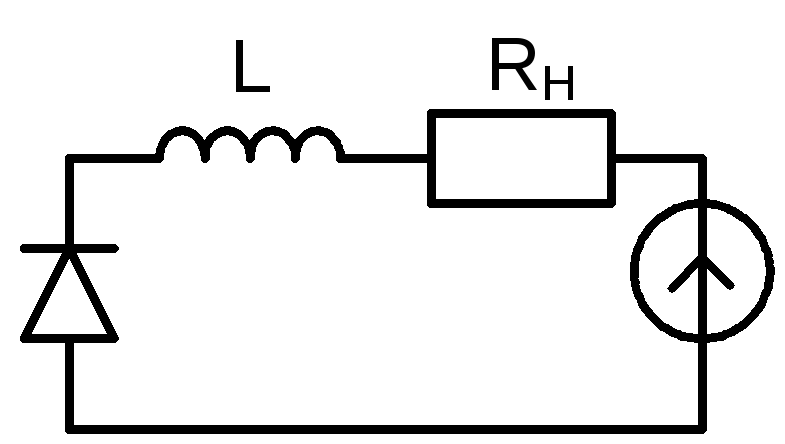
Эквивалентная схема режима постоянного тока имеет вид. Если (R₂=R_д+R_н), то состояние цепи описывается уравнениями:

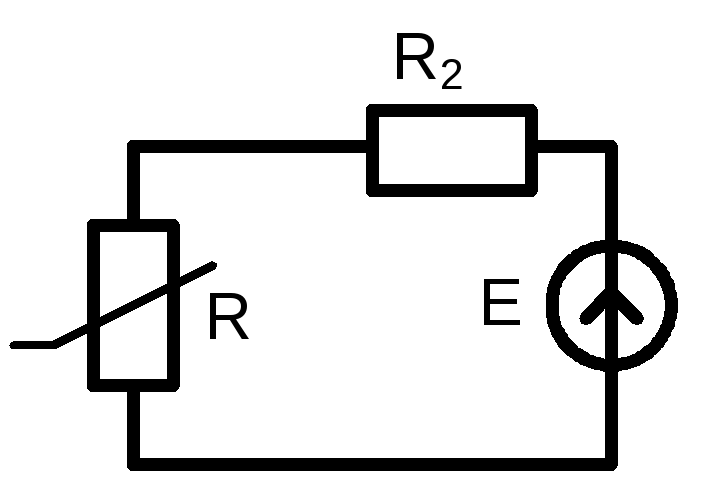
решение которых можно найти графическим методом.

Выберем рабочую точку на падающем участке характеристики. Возможное расположение нагрузочных линий представлено на рисунке.

Для режима колебаний эквивалентная схема представлена на рисунке. Уравнение цепи имеет вид:

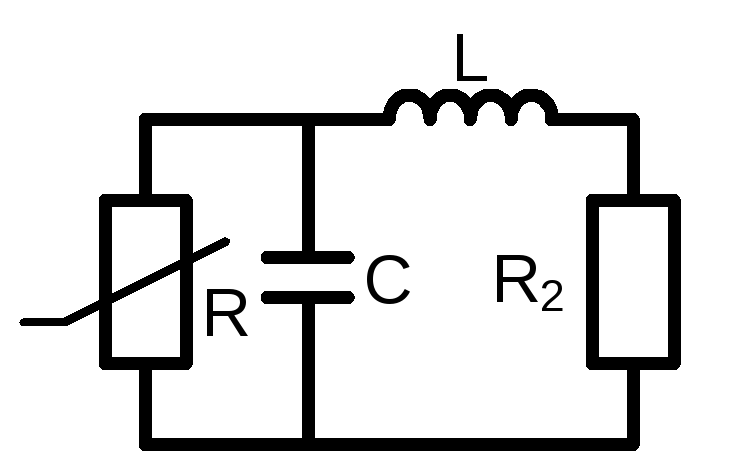
Характеристическое уравнение цепи определяется выражением

p²LC + p(LG_1диф + R₂C) + R₂G_1диф + 1=0 или

,

a₀p² + a₁p + a₂=0.

Определитель Рауса–Гурвица имеет следующий вид: . Состояние цепи является устойчивым, еслиD₁=a₁>0 и D₂=a₁a₂>0, т.е. если a₁>0 и a₂>0. Для коэффициента а₂ имеем >0. Учтем, что рабочая точка расположена на падающем участке характеристики, т.е.R_1диф<0 или . Тогда>0. Откуда для устойчивости рабочей точки по постоянному току имеем. Рассматривая коэффициентa₁ получаем, что для того чтобы а₁>0, необходимо чтобы ; т.е.;. Учитывая, что- эквивалентное сопротивление параллельного контура при резонансе, условие устойчивости запишем в виде:.

Если рассмотренную цепь использовать для усиления колебаний, необходимо обеспечить устойчивость: и положения рабочей точки и колебаний.

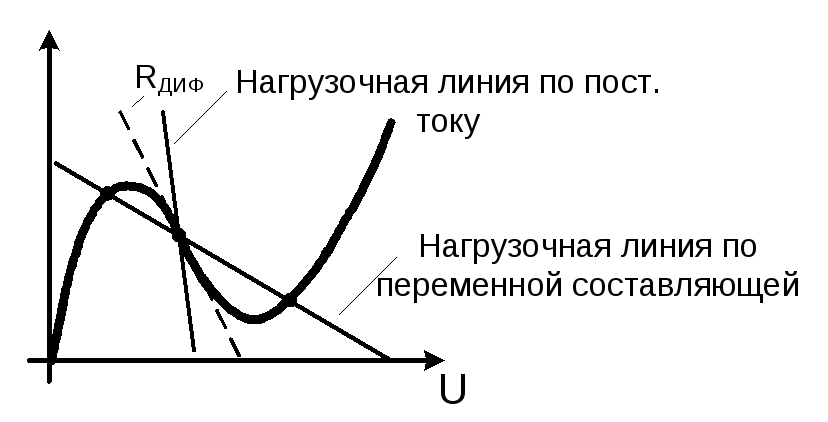i=φ(u)

Если цепь использовать для генерирования колебаний, необходимо обеспечить устойчивость рабочей точек (R₂<|R_1диф|) и неустойчивость колебаний (R_э.р.>|R_1диф|)

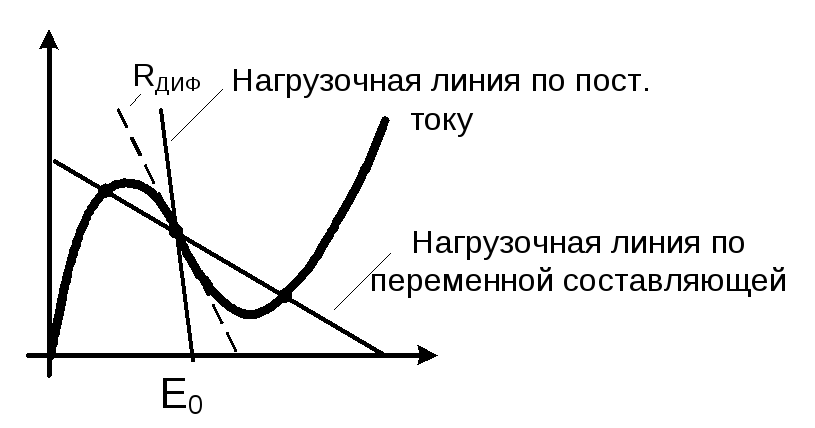i=φ(t)

Следует заметить, что оба режима использования схемы требуют выполнение условия R₂<|R_1диф| т.е. выполнение условия устойчивости положения рабочей

т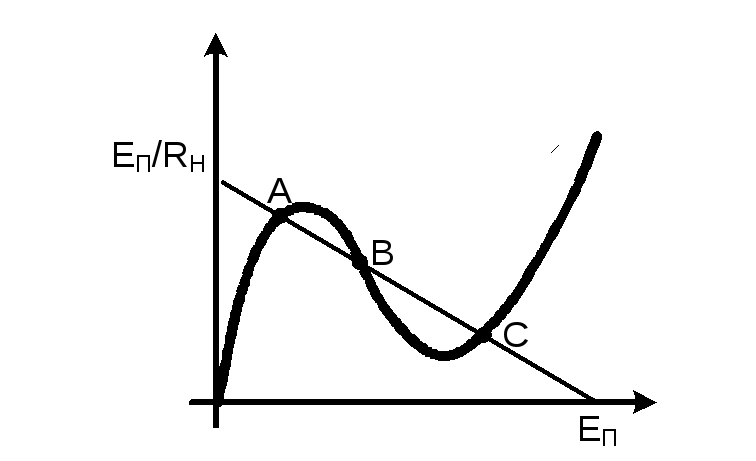очки. Если это условие не выполнять, т.е. еслиR₂>|R_1диф|, нагрузочная линия пересекает вольтамперную характеристику в трех точках при этом состояние цепи в т.А не устойчиво. При малейшем колебании цепь перейдет в состояние определяемое точками т.В или т.С

Метод линеаризации позволил выяснить условие, при котором в цепи могут возникнуть автоколебания, но этот метод не позволяет определить амплитуду установившихся колебаний. С этой задачей справится метод гармоничной линеаризации.