
- •Глава 1.
- •§1.1.Преобразование Лапласа и его основные свойства.
- •§ 1.2. Применение операторного метода для анализа процессов в цепях сосредоточенными элементами.
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях.
- •§1.4. Свободные колебания в динамических системах с распределенными элементами
- •§1.4.1.Классификация длинных линий
- •§1.4.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •§1.4.Алгоритмы решения задачи о собственных колебаниях в длинной линии
- •Глава 2. Колебания в линейных праметричеких
- •§ 2.1. Линейные спектра входного сигнала, при прохождении через линейные параметрические цепи.
- •§ 2.2. Аксиоматики теории цепей в параметрическом случае.
- •§2.3. Прохождение сигналов через параметрические r – цепи.
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с обной степенью свободы. Энергетическое рассотрение стационарных колебаний в системах с одной степенью свободы.
- •§ 2.5.1. Процессы в параметрической колебательной системе с обной степенью свободы.
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы.
- •§2.5.Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье.
- •2.6. Параметрическое усиление колебаний в одноконтурной системе.
- •§2.2.4 Параметрический генератор(параметрон).
- •§2.2. Двухконтурные параметрические системы.
- •§2.2.1Теорема Менли-Роу.
- •§ 2.2.2 Параметрические умножение и деление частоты.
- •§2.4. Некоторые приближенные методы исследования процессов в. Параметрических системах
- •§2.4.1. Метод «замороженного» параметра.
- •§2.4.1 Метод замороженного параметра.(второй вариант).
- •§2.4.2 Метод последовательных приближений.
- •§2.4.2. Метод последовательных приближений (второй вариант).
- •§2.4.3 Метод вкб.
- •§2.4.3. Метод вкб (Вентцеля-Крамерса-Бриллюэна)(второй вариант).
- •Глава 3. Анализ колебаний в нелинейных цепях.
- •3.1 Нелинейные элементы цепей
- •§3.2.Особенности задач анализа колебаний в нелинейных цепях.
- •§3.3. Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений.
- •§3.4. Метод линеаризации.
- •§3.2. Метод гармонической линеаризации (мгл).
- •§3.2.1. Эквивалентные параметры нелинейных элементов.
- •§3.3.Методы малого параметра. Метод последовательных приближений.
- •§3.4.Метод медленно меняющихся амплитуд (ммма).
- •§3.5.Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде.
- •§3.6.Метод фазовой плоскости.
- •1.Метод изоклин.
- •2.Особые точки.
§ 1.2. Применение операторного метода для анализа процессов в цепях сосредоточенными элементами.
Процессы в электрических цепях с сосредоточенными элементами носят колебательный характер и описываются электрическими колебаниями напряжений и токов в различных частях цепи. Эти колебания описывают скалярными функциями времени (t) и обозначают: u(t) – мгновенное значение напряжения, i(t) – мгновенное значение некоторого электрического колебания вообще.
Задача анализа процессов в цепи сводится к задачи Коши, т.е. к решению системы интегро-дифференциальных уравнений с заданными начальных условиями Для линейной цепи, составленной из постоянных элементов, система уравнений является линейной с постоянными коэффициентами.
При исследовании процессов свободных колебаний в цепях, а также исследовании вынужденных колебаний, решение системы уравнений удобно находить операторным методом, т.к. функции описывающие источники колебательного процесса – воздействия, а, следовательно, и функции, описывающие возникающие колебания – отклики, преобразуемы по Лапласу.
При использовании операторного метода для решения задач теории цепей удобно осуществить преобразование Лапласа для основных соотношений, составляющих аксиоматику теории цепей. Это позволяет миновать этап составления интегро-дифференциальных уравнений.
Пусть
функции, описывающие источники
колебательного процесса преобразуемы
по Лапласу. Обозначим изображения
напряжений в цепи U(p)=![]() [u(t)],
изображения
токов I(p)=
[u(t)],
изображения
токов I(p)=![]() [i(t)].
Назовем их
в дальнейшем операторными напряжениями
и операторными токами. Осуществим
преобразование Лапласа для выражений,
характеризующих основные идеальные
элементы цепей (см. Таблицы 1). Введем
понятие: операторное задающее напряжение
E(p)=
[i(t)].
Назовем их
в дальнейшем операторными напряжениями
и операторными токами. Осуществим
преобразование Лапласа для выражений,
характеризующих основные идеальные
элементы цепей (см. Таблицы 1). Введем
понятие: операторное задающее напряжение
E(p)=![]() [e(t)];
операторный задающий ток I(p)=
[e(t)];
операторный задающий ток I(p)=![]() [i(t)];
операторные сопротивления Z(p)
и операторные
проводимости Y(p)
основных
элементов и двухполюсников вообще.
Условимся описывать ненулевые начальные
условия для элементов индуктивности и
емкости источниками напряжения или
тока с соответствующими операторными
задающими характеристиками (см. Таблицу
1). Тогда для любых линейных цепей с
помощью метода контурных токов или
метода узловых напряжений можно записать
систему уравнений в операторной форме:
[i(t)];
операторные сопротивления Z(p)
и операторные
проводимости Y(p)
основных
элементов и двухполюсников вообще.
Условимся описывать ненулевые начальные
условия для элементов индуктивности и
емкости источниками напряжения или
тока с соответствующими операторными
задающими характеристиками (см. Таблицу
1). Тогда для любых линейных цепей с
помощью метода контурных токов или
метода узловых напряжений можно записать
систему уравнений в операторной форме:
![]() -
система контурных уравнений
-
система контурных уравнений
или
![]() -
система узловых напряжений
-
система узловых напряжений
Составленные
системы уравнений являются алгебраическими,
причем их правые части
![]() и
и
![]() содержат как изображение возбуждающих
источников (
содержат как изображение возбуждающих
источников (![]() или
или![]() ),
так и изображения ненулевых начальных
условий (
),
так и изображения ненулевых начальных
условий (![]() или
или![]() ).
При этом
).
При этом![]() ,
а
,
а![]() .
.
В теории цепей с сосредоточенными элементами выделяют две ключевые задачи анализа: исследование свободных колебаний в цепи и исследование прохождения сигнала через цепь. Важным частным случаем этих задач является исследование переходных процессов в цепи. В более общих случаях решение представлятся линейной комбинацией решений ключевых задач.
Таблица 1
|
Основные идеальные элементы цепей |
Их операторные характеристики | ||
|
i(t)=j(t) j(t) i(t)
|
I(p)=J(p) I(p) J(p)
| ||
|
U(t)=R
I(t)=G u(t)
R i(t) |
U(p)=R ZR(p)=R; YR(p)=G; ZR(p)=R I(p)
U(p)
| ||
|
U(t)=L i(t)= L i(t)
|
Нулевые начальные условия
U(p)=pLI(p);
I(p)=
Zp(p)=pL;
Yp(p)= Zp(p)=pL I(p)
U(p) |
Ненулевые начальные условия U(p)=pLI(p)-Li(0); Zp(p)=pL E(p)= =Li(0)
I(p) U(p) I(p)=
| |
|
i(t)=C u(t)=
C i(t)
U(t) |
Нулевые начальные условия
I(p)=pCU(p);
U(p)=
Zc(p)=
ZC(p)=
U(p)
|
Ненулевые начальные условия I(p)=pCU(p)-Cu(0);
J I(p) YC(p)=pC
U(p) U(p)=
U(p)
| |
















 Источник
тока
Источник
тока






 Активное
сопротивление
Активное
сопротивление



















 Индуктивность
Индуктивность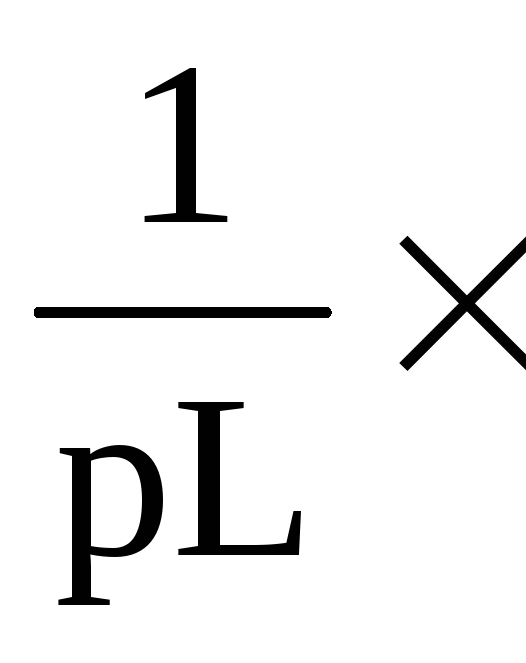 U(p);
U(p);






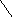
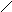
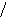




























 Емкость
Емкость