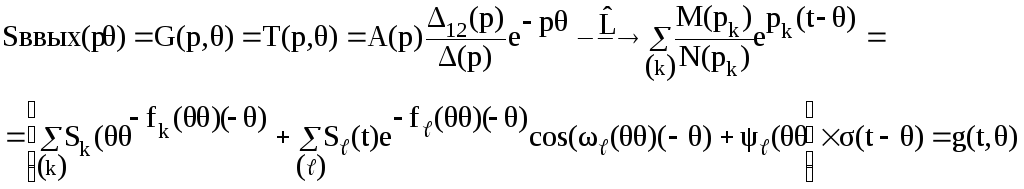- •Глава 1.
- •§1.1.Преобразование Лапласа и его основные свойства.
- •§ 1.2. Применение операторного метода для анализа процессов в цепях сосредоточенными элементами.
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях.
- •§1.4. Свободные колебания в динамических системах с распределенными элементами
- •§1.4.1.Классификация длинных линий
- •§1.4.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •§1.4.Алгоритмы решения задачи о собственных колебаниях в длинной линии
- •Глава 2. Колебания в линейных праметричеких
- •§ 2.1. Линейные спектра входного сигнала, при прохождении через линейные параметрические цепи.
- •§ 2.2. Аксиоматики теории цепей в параметрическом случае.
- •§2.3. Прохождение сигналов через параметрические r – цепи.
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с обной степенью свободы. Энергетическое рассотрение стационарных колебаний в системах с одной степенью свободы.
- •§ 2.5.1. Процессы в параметрической колебательной системе с обной степенью свободы.
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы.
- •§2.5.Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье.
- •2.6. Параметрическое усиление колебаний в одноконтурной системе.
- •§2.2.4 Параметрический генератор(параметрон).
- •§2.2. Двухконтурные параметрические системы.
- •§2.2.1Теорема Менли-Роу.
- •§ 2.2.2 Параметрические умножение и деление частоты.
- •§2.4. Некоторые приближенные методы исследования процессов в. Параметрических системах
- •§2.4.1. Метод «замороженного» параметра.
- •§2.4.1 Метод замороженного параметра.(второй вариант).
- •§2.4.2 Метод последовательных приближений.
- •§2.4.2. Метод последовательных приближений (второй вариант).
- •§2.4.3 Метод вкб.
- •§2.4.3. Метод вкб (Вентцеля-Крамерса-Бриллюэна)(второй вариант).
- •Глава 3. Анализ колебаний в нелинейных цепях.
- •3.1 Нелинейные элементы цепей
- •§3.2.Особенности задач анализа колебаний в нелинейных цепях.
- •§3.3. Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений.
- •§3.4. Метод линеаризации.
- •§3.2. Метод гармонической линеаризации (мгл).
- •§3.2.1. Эквивалентные параметры нелинейных элементов.
- •§3.3.Методы малого параметра. Метод последовательных приближений.
- •§3.4.Метод медленно меняющихся амплитуд (ммма).
- •§3.5.Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде.
- •§3.6.Метод фазовой плоскости.
- •1.Метод изоклин.
- •2.Особые точки.
§ 2.2.2 Параметрические умножение и деление частоты.
В случае, когда частоты становятся порядка
1 Ггц, то транзисторы перестают работать
и проблема умножения частоты на СВЧ
диапазоне сильно усложняется. Хотя в
СВЧ диапазоне транзисторы не работают,
но диоды продолжают работают, Тогда
включая диод между двумя резонаторами
можно получить умножение частоты и
причем коэффициент передачи будет
случае, когда частоты становятся порядка
1 Ггц, то транзисторы перестают работать
и проблема умножения частоты на СВЧ
диапазоне сильно усложняется. Хотя в
СВЧ диапазоне транзисторы не работают,
но диоды продолжают работают, Тогда
включая диод между двумя резонаторами
можно получить умножение частоты и
причем коэффициент передачи будет![]() ,
гдеn
номер гармоники.
,
гдеn
номер гармоники.
В диапазоне, меньше чем СВЧ умножение частот осуществляется с использованием обычного резонансного усилителя, работающего в нелинейной области ВАХ транзистора. При этом можно получать умножение до 10 раз. С помощью параметрических систем можно осуществить умножение и деление частот с высоким коэффициентом деления (имеется в виду высоким kp=1)
§2.3.Энергетическое рассмотрение 2-х контурного параметрического усилителя регенеративного типа. Определение критического коэффициента модуляции, вносимого сопротивления и коэффициента передачи на резонансной частоте.
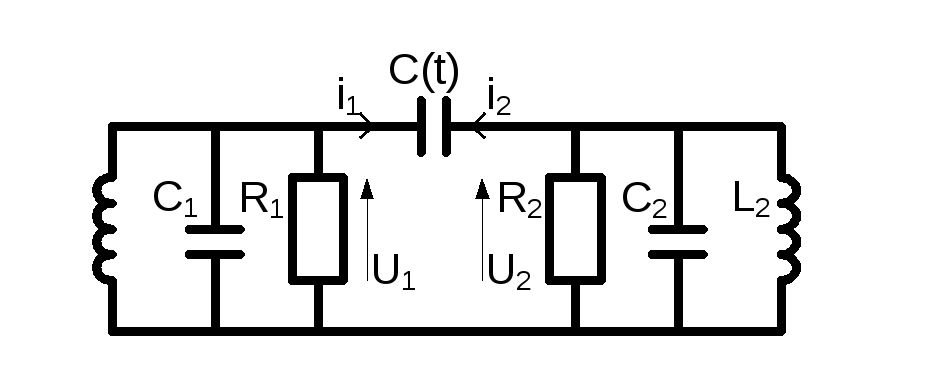
ω1=ωс ω2=ωн-ω1
![]() ;
т.к.
;
т.к.
![]()
![]() -
считается заданным
-
считается заданным
![]()
Первый контур имеет комплексное сопротивление Z1(ω) , а второй Z2(ω).
Будем считать, что
![]()

Тогда
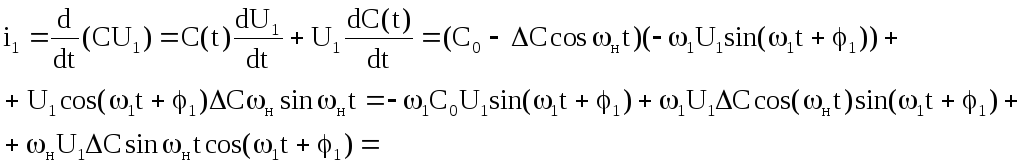

![]()

![]()

Последняя составляющая приведет к появлению напряжения на втором контуре, т.к. у него ω2 – резонансная частота.
![]() где
где
![]()
З а
счет резонансных свойств, возникло
напряжениеU2
на
сопротивлении
второго
контура,
которое будет приложено
к переменной
емкости
и Z1(ω),
но
а
счет резонансных свойств, возникло
напряжениеU2
на
сопротивлении
второго
контура,
которое будет приложено
к переменной
емкости
и Z1(ω),
но
![]() и
поэтому
и
поэтому![]() пренебрегаем по сравнению с
пренебрегаем по сравнению с![]()
Z1(ω2) Z2(ω2) U2
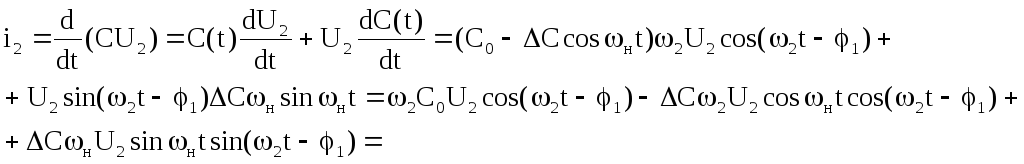

![]()

![]()
![]()
Вводим
настоящий ток, протекающий через емкость.
В нашей системе отсчета он равен
![]()
![]() На
частоте ω1
мы выделяем слагаемые с частотой ω1,
их остается 2. Рассмотрим
На
частоте ω1
мы выделяем слагаемые с частотой ω1,
их остается 2. Рассмотрим
![]()
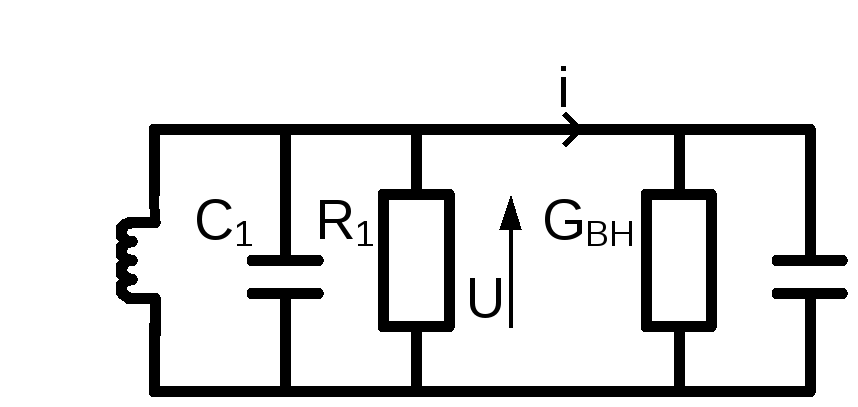
L1 C0
![]()
![]()
![]()
![]()
На
резонансной частоте ω1
у нас в
Z1(ω1)
присутствует только активное сопротивление,
причем теперь мы можем сказать чему
равна резонансная частота первого
контура
![]() ,
а проводимость
,
а проводимость![]()
При
m=mкр
![]()

Для
параллельного контура
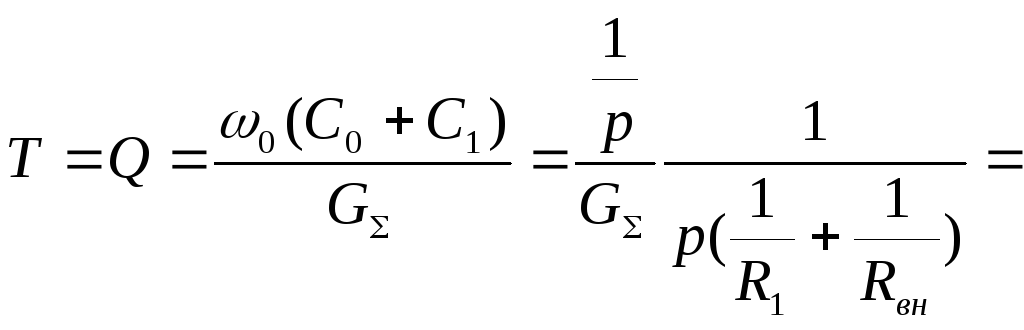
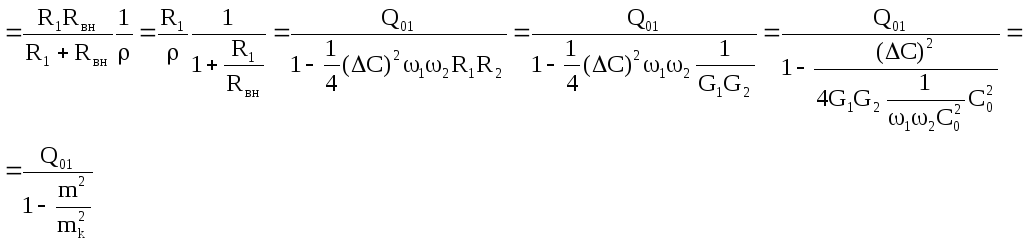

Отметим важную особенность: усилительные свойства 2х контурных параметрических усилителей в отличие от одноконтурных не зависят от сдвигов фаз между сигналом и накачкой.
§2.4. Некоторые приближенные методы исследования процессов в. Параметрических системах
§2.4.1. Метод «замороженного» параметра.
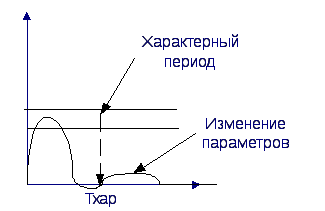
Применяются при очень медленном изменении параметров по сравнению с характерным периодом колебаний в системе.
 Система
уравнений
Система
уравнений
![]()
Полагаем
![]() ,
т.е. полагаем значение элементов
постоянными- «замороженными» и решаем
полученную систему уравнений с постоянными
коэффициентами.
,
т.е. полагаем значение элементов
постоянными- «замороженными» и решаем
полученную систему уравнений с постоянными
коэффициентами.![]() .
Применим преобразование Лапласа
.
Применим преобразование Лапласа![]() к нашей системе уравнений, и получаем
к нашей системе уравнений, и получаем![]() ,
откуда находим
,
откуда находим
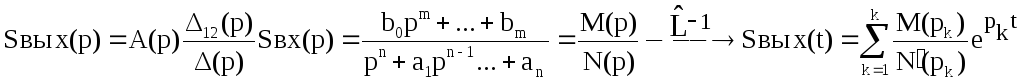
где b=b(R,G,L,C); a=a(R,G,L,C) рa=рa(R,G,L,C).
«Размораживаем» параметры, т.е. полагаем их функциями от параметра t, а следовательно коэффициенты становятся также функциями параметра t, т.е. b=b(t), a=a(t) и корни рk=рk(t). Поэтому окончательно получаем для Sвых:
Sвых
=
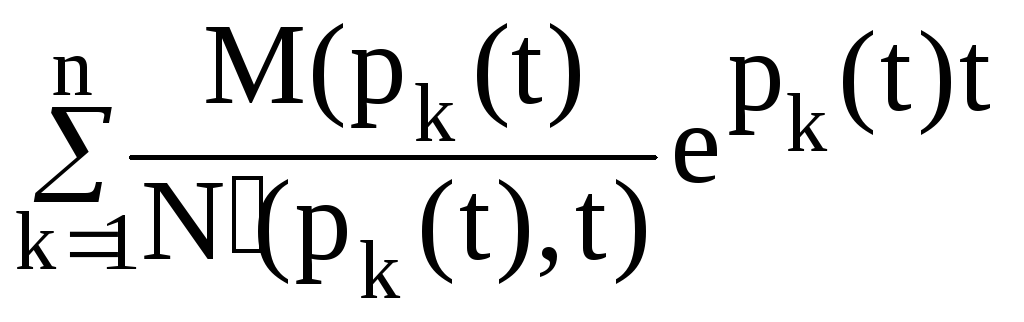
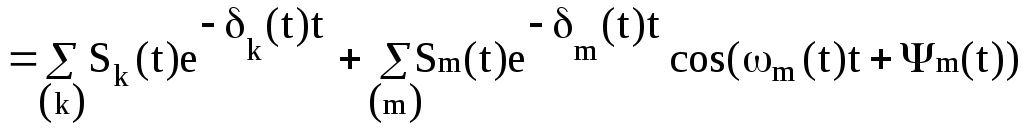
Определяем импульсную функцию для случая m<n.
![]() ,
,