
- •Красноярск 2006
- •Предисловие
- •1. Неопределенный и определенный интегралы
- •1.1. Определение неопределенного интеграла. Методы интегрирования
- •Решение:
- •Применяя указанные формулы, получим
- •1.2.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
- •Понятие определенного интеграла
- •Свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Теорема. Если функция f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке, то имеет место следующая формула:
- •Метод замены переменной в определенных интегралах
- •Метод интегрирования по частям в определенных интегралах
- •Вычисление площадей плоских фигур
- •Параметрические функции
- •Вычисление длины дуги плоской кривой
- •Вычисление площади поверхности вращения
- •Объем тела вращения
- •1.3 Несобственные интегралы
- •2.3 Задания на контрольную работу
- •3.1.Общая методология интегралов
- •3.2. Двойной интеграл
- •Правила вычисления двойного интеграла в полярной системе координат
- •3.3. Тройной интеграл
- •3. 4. Криволинейные интегралы
- •3.5. Поверхностные интегралы
- •7. Элементы теории поля
- •Понятие функции комплексного переменного
- •Предел и непрерывность функции комплексного переменного
- •Производная ФКП. Условия Коши-Римана
- •Интегрирование ФКП
- •Ряд Лорана
- •Особые точки
- •Вычеты
- •Преобразование Лапласа
- •4.2.Решение типовых примеров и задач
- •4.3.Задания на контрольную работу
- •5.1.1.Классификация линейных дифференциальных уравнений в частных производных второго порядка
- •5.1.2.Начальные и краевые условия
- •5.1.3.Уравнение колебаний струны
- •5.1.4.Уравнение теплопроводности
- •5.1.5.Уравнение Лапласа
- •5.2. Решение типовых примеров и задач
- •5.3. Задания на контрольную работу
- •10. Ряды
- •Задание 2. Найти область сходимости рядов:
- •Практикум по математике
- •4.1.Краткие сведения из теории
- •Комплексные числа

|
Решение. |
а) Вычислим |
|
площадь поверхности, |
||||||||||
|
полученной вращением отрезка прямой |
y = x (0 ≤ x ≤ R) |
||||||||||||
|
вокруг оси |
Ox |
(рис. |
1.15). |
|
Найдем |
производную: |
|||||||
Рис. 1.15 |
y′ = (x)′ = 1. Подставляя в формулу (1.6) получим: |
|||||||||||||
|
||||||||||||||
|
R |
|
R |
|
|
x2 |
|
|
R |
|
|
|||
|
|
|
|
|
|
|
||||||||
S = 2π ∫x 1 + 12 dx = 2π |
2 ∫xdx = 2 |
|
|
|
|
|
= 2π R2 . |
|||||||
|
2π |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
0 |
|
0 |
|
|
2 |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
||||||||
б) В параметрической форме формулу (1.6) можно записать в |
||||||||||||||
следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
′ |
|
2 |
|
′ |
(x)] |
2 |
dt . |
(1.7) |
|||
|
|
|
|
|
||||||||||
|
S = 2π∫y(t) [x (t)] |
|
+[y |
|
||||||||||
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда площадь поверхности, образованной вращением одной арки циклоиды вокруг оси Ox, будет равна
2π
S = 2π ∫ a(1 − cost) (asin t)2 + a2 (1 − cost)2 dt =
0 |
|
|
2π |
64 |
|
= 2 2π a2 ∫( 1 − cost)3/ 2 dt = |
πa2 . |
|
0 |
3 |
|
|
|
Объем тела вращения
Если площадь S(x) сечения тела плоскостью, перпендикулярной оси
Ox, является непрерывной функцией на отрезке [a; b], то объем тела вычисляется по формуле:
b |
|
V = ∫S(x)dx . |
(1.8) |
a
Выражение для функции S(x) получается достаточно просто в случае тел вращения. Если криволинейная трапеция, ограниченная кривой y = f (x), a ≤ x ≤ b , вращается вокруг оси Ox или оси Oy, то объемы тел
28
вращения вычисляются по формулам:
b |
b |
|
Vx =π ∫ f 2 (x)dx или |
Vy =π ∫ϕ2 ( y)dy . |
(1.9) |
a |
a |
|
Если криволинейный сектор, ограниченный кривой ρ = ρ(ϕ) и лучами ϕ =α , ϕ = β , вращается вокруг полярной оси, то объем тела вращения равен:
β
Рис. 1.16 V = 2 π ∫ρ3 sinϕdϕ . (1.10)
3 α
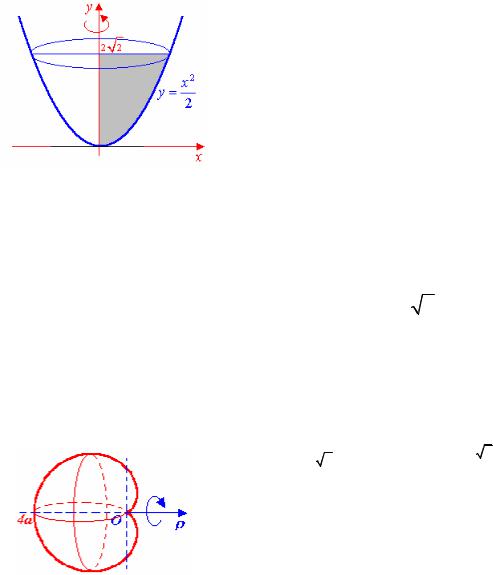
Пример. Найти объем тела, образованного вращением фигуры,
ограниченной а) |
линиями |
y = |
x2 |
, x =0, y = 2 |
2 |
|
вокруг |
оси Oy; б) |
||||||||
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кардиоидой ρ = 2a(1 − cosϕ) |
вокруг полярной оси. |
|
|
|
|
|
|
|
|
|||||||
Решение. а) Используя формулу (1.9), найдем объем данного тела (рис. |
||||||||||||||||
1.16): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
y2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Vy =π ∫ 2 ydy = 2π |
|
|
|
|
3 |
|||||||||
|
|
|
|
|
|
|
|
= |
8π (ед. ) |
|||||||
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
б) Используя формулу (1.10), найдем объем |
||||||||||||||
Рис. 1.17 |
данного тела (рис.1.17): |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
V = 2 π |
π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∫(2a(1 − cosϕ))3 sinϕdϕ = |
|||||||||||
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
16a3 π ∫(1 − cosϕ)3 d (1 − cosϕ) = |
||||||||||
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 16a3 |
π (1 − cosϕ)4 |
|
π |
= 16a3 π |
4 = 64 |
πa3 |
= 21 |
1πa3 . |
||||||||
|
||||||||||||||||
3 |
4 |
|
|
0 |
|
|
3 |
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
29
1.3 Несобственные интегралы
Несобственными интегралами называются: 1) интегралы с бесконечными пределами (несобственные интегралы 1-го рода); 2)
интегралы от неограниченных функций (несобственные интегралы 2-го рода).
Несобственный интеграл от функции f (x) в пределах от a до +∞
определяется равенством
+∞
∫
a
b |
|
f (x)dx = blim→+∞∫ f (x)dx . |
(1.11) |
a |
|
Если этот предел существует и конечен, то интеграл называется сходящимся, если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
Аналогично определяются:
a |
|
a |
|
+∞ |
|
b |
|
∫ |
f (x)dx = blim→−∞∫ f (x)dx и |
∫ f (x)dx = blim→+∞∫ f (x)dx . |
(1.12) |
||||
−∞ |
|
b |
|
−∞ |
|
a→−∞a |
|
Если функция имеет бесконечный разрыв в точке c отрезка [a;b] и |
|||||||
непрерывна при |
a ≤ x < c и |
при |
c < x ≤ b , |
то несобственный интеграл 2-го |
|||
рода определяется следующим равенством: |
|
|
|
|
|||
|
b |
|
c−ε |
|
b |
|
|
|
∫ f (x)dx = |
εlim→0 |
∫ f (x)dx + |
εlim→0 |
∫ |
f (x)dx . |
(1.13) |
|
a |
|
a |
|
c+ε |
|
|
Несобственный интеграл 2-го рода называется сходящимся, если оба предела в правой части существуют и конечны; если же хотя бы один из интегралов не существует или бесконечен, то несобственный интеграл называется расходящимся.
Пример. Вычислить несобственные интегралы (или установить их
30

|
|
+∞ |
+∞ |
dx |
|
1 |
|
|||
расходимость): а) |
∫ sin xdx ; б) |
∫ |
|
; |
в) ∫dx . |
|||||
|
2 |
|||||||||
|
|
0 |
−∞ 1 |
+ x |
|
0 |
x |
|||
|
Решение. а) Согласно формуле (1.12) |
получим |
||||||||
+∞ |
b |
|
|
|
|
|
b |
= lim (−cosb + 1)=1 − lim cosb , |
||
|
sin xdx = lim |
sin xdx = lim (−cos x) |
|
|||||||
|
|
|||||||||
∫ |
b→+∞ ∫ |
b→+∞ |
|
|
|
|
0 |
|
b→+∞ |
b→+∞ |
|
|
|
|
|||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
т.е. предел не существует и несобственный интеграл расходится.
б) Используя четность подынтегральной функции и формулу (1.12), получим:
+∞ |
dx |
|
+∞ |
dx |
|
|
b |
dx |
|
|
|
0b = 2 lim arctgb = 2 |
π |
|
∫ |
|
= 2 ∫ |
|
= 2 lim |
∫ |
|
= 2 lim arctg x |
|
=π . |
|||||
|
|
|
|
|||||||||||
1 + x |
2 |
1 + x |
2 |
1 + x |
2 |
2 |
||||||||
−∞ |
|
0 |
|
b→+∞ |
0 |
|
b→+∞ |
|
b→+∞ |
|
Следовательно, несобственный интеграл сходится и равен π .
в) Используя формулу (1.13), получим:
1 |
|
|
1 |
|
|
|
|
∫dx |
= lim |
∫dx |
= lim ln x |
|
ε1 = lim (−lnε) = +∞ . |
||
|
|||||||
0 |
x |
ε→+0 |
ε |
x |
ε→+0 |
|
ε→+0 |
Следовательно, несобственный интеграл расходится.
1.4. Задания на контрольную работу Задание 1.. Найти неопределенные интегралы. Первый и второй проверить дифференцированием.
1. а) |
∫2−2x+1 dx, |
б) ∫ x3x dx, |
|
|
в) ∫ |
|
|
2x2 −1 |
dx, |
||||
|
|
x |
3 |
− 5x |
2 |
+6x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
г) ∫ |
dx |
, д) ∫ |
|
|
dx |
|
, |
|
|
|
|
|
|
3 − 2sinx + cosx |
x |
3 |
1 + x |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
31
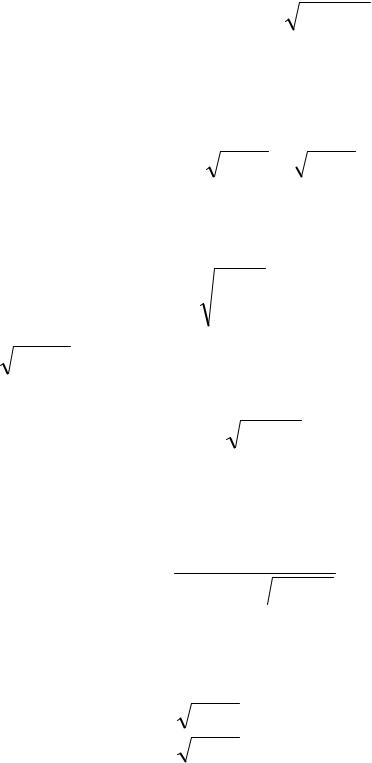
2. а) |
∫ |
2xdx |
, |
|
|
|
||
2 |
|
|
|
|||||
|
|
x |
|
+ 2 |
|
|
|
|
г) ∫ |
|
|
|
dx |
|
|
|
, |
sin |
2 |
xcos |
4 |
x |
||||
|
|
|
|
|||||
3. а) ∫sin3 x cos xdx,
г) ∫ |
|
dx |
|
, |
|
3cos x + 2 |
|||||
|
|
||||
4. а) |
∫ |
ln2 x |
dx, |
|
|
x |
|
||||
г) |
∫tg2 xsin2 xdx, |
|
||||||
5. |
а) |
∫ |
|
arctgx |
dx , |
|
||
1 + x2 |
|
|||||||
г) |
∫tg6 xdx, |
|
|
|||||
6. |
а) |
∫ex3 x2dx, |
б) |
|||||
г) |
∫ |
cos2 x |
dx, |
|
||||
sin |
6 |
x |
|
|||||
|
|
|
|
|
|
|||
б) ∫ x2 sin 3xdx, |
|
в) |
∫ |
x3 −2x2 +4 |
dx, |
|||||||||||||||||||||||||
|
|
x |
3 |
(x |
− |
|
|
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|||||||||||||
д) ∫ |
|
|
|
dx |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 |
− a2 ) x2 − a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
б) ∫(x2 − 2x)e−xdx, |
в) |
∫ |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
, |
|
|||||||||
|
x |
4 |
+ 2x |
2 |
+ |
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
д) ∫ |
|
xdx |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x +1 |
+ 3 |
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
б) ∫(5 − x)exdx, |
|
|
|
|
в) |
∫ |
|
|
x4 +1 |
dx, |
|
|||||||||||||||||||
|
|
|
|
|
|
x |
2 |
−1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
д) ∫ |
|
1 − x dx |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 + x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) ∫(3x2 +5)ln xdx, |
|
|
|
|
в) |
|
∫ |
|
|
|
|
dx |
|
|
|
, |
|
|
|
|||||||||||
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+8 |
|
|
|
|
|
||||||
д) ∫ x2 |
4 − x2 dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫(5x +1)e2xdx, |
в) |
∫ |
|
x4 +3x3 +3x2 −5 |
dx, |
|||||||||||||||||||||||||
|
x |
3 |
+ |
3x |
2 |
|
+3x + |
1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
dx
д) ∫(x2 +16) 9 − x2 ,
9 − x2 ,
7.а) ∫6xsin(x2 +3)dx, |
б) ∫(2x −1)2x dx, в) |
∫ |
x2 |
− x +4 |
|
|
dx, |
|||
(x +1)(x −2)(x |
−3) |
|||||||||
|
|
|
|
|
|
|||||
г) ∫sin4 xcos4 xdx, |
д) ∫ |
x +1 +1 |
dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x +1 −1 |
|
|
|
|
|
|
||
32

|
8. а) |
∫ |
|
|
|
|
|
tgx |
|
|
|
|
dx , |
|
б) ∫ x5x dx, |
|
|
|
в) ∫ |
|
|
|
4x(x −2) |
|
dx, |
||||||||||||||||||||||
|
|
cos |
2 |
|
x |
|
|
|
|
|
(x |
|
2 |
|
|
2 |
+ |
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1) (x |
|
1) |
|
|
||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
x + 3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
г) |
∫ |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
д) |
∫ |
|
|
|
|
|
|
dx, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
sin |
4 |
|
x |
|
|
|
|
|
|
|
|
x(1 + |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
9.а) |
∫ |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
,б) ∫(x3 + 5x −1)lnxdx, в) ∫ |
|
|
|
2x |
|
|
|
dx, |
|||||||||||||||||||
|
(1+ x |
2 |
|
)arctgx |
|
(x +1)(x |
2 |
|
|
2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1) |
|
||||||||||||||||||||||||||
|
г) ∫ |
cos3 x |
dx, |
|
д) |
∫ |
|
|
x |
|
|
dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
sin |
4 |
x |
|
|
x − |
3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫e |
1 |
|
dx2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
10. |
|
|
|
а) |
|
|
|
|
|
x |
|
|
|
|
|
|
б) |
∫ x2 cos xdx, |
|
|
|
|
|
|
|
в) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ |
2x2 −3x −3 |
|
|
|
|
|
|
dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(x −1)(x2 −2x +5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
г) |
∫sin4 xdx, |
|
|
|
|
д) |
∫ |
|
dx |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задание 2. Вычислить определенный интеграл. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
dx |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
б) ∫x cos3xdx |
|
|
|
|
|
||||||||||||||
|
1. а) |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
3 |
|
+ |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
cos(lnx)dx |
, |
|
|
|
|
|
|
|
|
|
|
1/2 |
x |
dx |
|
|
|
|
|||||||||||||||
|
2. |
|
|
а) ∫ |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
б) ∫x e |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3. а) |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
б) ∫x sinxdx |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
xlnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
exdx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4. а) ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
б) ∫x 5 |
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||
|
e |
2x |
+ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
33

e2 |
2 + lnxdx |
|
|
5. а) ∫ |
, |
||
x |
|||
1 |
|
1x2dx
6.а) ∫0 4 + x3 ,
1
7. а) ∫x(2 + x2 )7 dx,
0
0dx
8.а) -∫1 1 + 3 x +1,
|
1/2arctg2xdx |
, |
||||
9. а) |
∫ |
1 + 4x |
2 |
|||
|
0 |
|
|
|||
|
2 |
exdx |
|
|
|
|
10.а) |
∫ |
|
|
, |
|
|
1 + e |
2x |
|
|
|||
|
1 |
|
|
|
|
|
Задание 3. Вычислить несобственный расходимость.
|
|
∞ |
|
|
|
||
1. |
а) ∫x e- x2 dx , |
||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2. |
а) ∫x2 ex3 dx , |
||||||
|
|
-∞ |
|
|
|
||
|
|
-3 |
|
|
xdx |
|
|
3. |
а) |
∫ |
|
, |
|
||
|
2 3 |
||||||
|
|
-∞(x |
+1) |
|
|
||
|
|
∞ |
dx |
||||
4. |
а) |
-∫1 |
|
|
|||
|
, |
||||||
x2 + x +1 |
|||||||
34
|
1/2 |
|
|
|
|
|
|
|
|
|
б) |
∫arcsin2xdx |
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
|
|
|
|
|
б) |
∫arctg2xdx |
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
π/4 |
|
|
|
|
|
|
||
|
б) |
∫x2 sinxdx |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
б) |
∫ln(x + 2)dx |
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
б) |
∫x lnxdx |
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
б) |
∫x arctgxdx . |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
интеграл |
или доказать его |
|||||||||
|
|
1 |
|
|
dx |
|
|
|
||
|
б) ∫0 |
|
|
|
, |
|||||
|
x2 − 4x + 3 |
|||||||||
|
|
2 |
|
|
dx |
|
|
|
|
|
|
б) |
∫ |
|
|
|
|
, |
|
||
|
|
(x - 1)2 |
|
|
||||||
|
|
0 3 |
|
|
|
|||||
|
|
2 |
|
|
xdx |
|
|
|
|
|
|
б) |
∫0 |
|
, |
|
|
|
|
||
|
x2 − 4 |
|
|
|
||||||
|
|
1 |
|
|
x2dx |
|
|
|
|
|
|
б) |
∫ |
|
|
|
|
, |
|
|
|
|
|
x3 − |
1 |
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
||

|
|
∞ arctgxdx |
|
|
|
2 |
|
|
|
dx |
|
|
|
|
|
|
|||||||||
5. |
а) ∫ |
|
|
|
|
2 |
|
|
|
|
, |
|
б) ∫ |
|
|
|
|
|
, |
|
|
||||
|
|
x |
+1 |
|
|
|
|
|
2 |
|
|
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
(x - 2) |
|
|
|
|
|
|
||||||||
|
|
∞ |
|
|
|
dx |
|
|
|
|
|
|
4 |
|
|
|
dx |
|
|
|
|
|
|||
6. |
а) ∫ |
|
|
|
|
, |
|
|
|
б) ∫ |
|
|
|
, |
|
|
|||||||||
x |
|
2 |
x |
|
|
|
|
|
3 |
|
|
||||||||||||||
|
|
2 |
ln |
|
|
|
|
|
3 |
(x - 3) |
|
|
|
|
|
|
|||||||||
|
|
∞ lnxdx |
|
|
|
|
|
|
2 |
|
|
|
dx |
|
|
|
|
|
|
||||||
7. |
а) |
∫ |
|
|
|
|
|
|
, |
|
|
|
|
б) |
∫ |
|
|
|
|
|
|
|
|
|
, |
|
|
|
x |
|
|
|
|
|
|
x |
2 |
− x |
− |
2 |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
|
∞ |
|
|
|
xdx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
8. |
а) |
∫ |
|
|
|
|
, |
|
|
б) |
∫lnxdx , |
|
|
|
|
|
|
||||||||
(x |
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
+1) |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∞ |
|
|
|
|
|
dx |
|
|
|
|
|
3 |
|
|
|
dx |
|
|
|
|
|
|
|
9. |
а) ∫ |
|
|
|
|
|
|
|
, |
б) ∫ |
|
|
|
|
|
, |
|
|
|||||||
|
|
2 |
− 4x +7 |
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
-∞ x |
|
|
|
|
1 |
(x − 2) |
|
|
|
|
|||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
dx |
|
|
|
|
||
10. |
а) |
∫e- |
|
x dx , |
|
|
|
|
б) |
∫ |
|
|
. |
|
|
||||||||||
|
|
|
|
|
3 |
x −1 |
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
||||
Задание 4. Задачи на геометрические приложения определенного интеграла.
1. |
Вычислить площадь фигуры, ограниченной параболами |
y = x2 + 1 , |
|||
y = |
1 |
x2 |
и прямой y = 5 . |
|
|
2 |
|
|
|||
2. |
Вычислить длину дуги параболы y2 = 4x от вершины |
до |
точки |
||
М(1;2). |
|
|
|
||
3. |
Вычислить объем тела, полученного вращением вокруг оси 0у |
||||
криволинейной трапеции, ограниченной гиперболой xy = 4 , прямыми |
y =1, |
||||
y= 2 и осью 0у.
4.Вычислить площадь фигуры, ограниченной линиями, заданными
x = 9cost
уравнениями , y = 2(y ≥ 2).
y = 4sint
5. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах r = cos2ϕ .
35
6 |
Вычислить |
длину |
дуги |
кривой, |
заданной |
параметрически |
|
|
x = 5(t − sint) |
, |
0 ≤ t ≤ π. |
|
|
||
уравнениями |
|
|
|
||||
|
y = 5(1 − cost) |
|
|
|
|
|
|
7. |
Вычислить длину дуги кривой, заданной уравнением в полярных |
||||||
координатах r = 2(1 - cosϕ) , - π ≤ϕ ≤ −π/2. |
|
|
|||||
8. |
Вычислить объем тела, полученного вращением вокруг оси 0x |
||||||
фигуры, ограниченной графиками функций y = −x2 + 5x −6, y =0. |
|||||||
9. |
Вычислить объем тела, полученного вращением вокруг оси 0у |
||||||
фигуры, ограниченной графиками функций y = x2 - 2x + 1, |
y =0, x = 2. |
||||||
10. Вычислить |
площадь |
фигуры, |
ограниченной кардиоидой |
||||
r = 3(1 + cosϕ) . |
|
|
|
|
|
|
|
36
2.Дифференциальные уравнения
2.1.Краткие сведения из теории
2.1.1.Дифференциальные уравнения первого порядка
Дифференциальное |
уравнение первого |
порядка |
имеет |
вид |
||||
|
dy |
, x – независимая переменная, y – искомая функция. |
|
|
||||
F x, y, |
|
= 0 |
|
|
||||
|
|
|
||||||
|
dx |
|
|
|
|
|
|
|
Дифференциальное |
уравнение вида f1 (x)g1 ( y)dx + f2 (x)g2 ( y)dy = 0 , |
где |
||||||
f1 (x), |
g1 ( y), |
f2 (x), g2 ( y) |
– |
непрерывные |
функции, |
называется |
||
дифференциальным уравнением с разделяющимися переменными и его
решение находится в виде: ∫ |
f1 |
(x) |
dx +∫ |
g1 |
( y) |
|
dy = C . |
|
|||
f2 |
|
g2 |
( y) |
|
|||||||
|
|
(x) |
|
|
|
|
|||||
Дифференциальное |
уравнение |
вида |
P(x, y)dx + Q(x, y)dy = 0 |
называется |
|||||||
однородным, если P(x, y) и Q(x, y) — однородные функции |
от x и y |
||||||||||
одинакового измерения. Оно решается подстановкой t = |
y |
. |
|
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
Дифференциальное |
|
уравнение |
вида y′+ P(x) y = Q(x) |
называется |
|||||||
линейным неоднородным уравнением. Оно решается подстановкой y = u v ,
где u = u(x) , v = v(x) .
Дифференциальное уравнение вида y′+ P(x) y = Q(x) ya , где a —
действительное число называется уравнением Бернулли. Во всех случаях оно сводится к линейному с помощью подстановки z = y1−a . При a=0, a=1
уравнение становиться неоднородным линейным.
2.1.2. Дифференциальные уравнения, допускающие понижения порядка
Уравнение вида F(x, y, y', y'',K, y(n) ) = 0 называется дифференциальным
уравнением n-го порядка. Интегрирование дифференциальных уравнений
37
n-го порядка (в конечном виде) удается произвести только для некоторых частных случаев.
Решение уравнение y(n) = f (x) находится интегрированием данного уравнения n раз.
y = ∫∫∫K∫ f (x)dxn + C1 xn−1 + C2 xn−2 +K+ Cn−1 x + Cn .
n раз
Порядок уравнения вида F(x, y(k ) , y(k −1) ,K, y(n) ) = 0 можно понизить, взяв за новую неизвестную функцию z = y(k ) , и таким образом понижаем порядок на k единиц.
Уравнение вида F( y, y', y'',K, y(n) ) = 0 допускает понижение порядка на единицу, если положить y' = z , а за новый аргумент принять сам y.
2.1.3. Линейные уравнения с постоянными коэффициентами.
Дифференциальное уравнение y(n) + a1 y(n−1) + a2 y(n−2) +K+ an−1 y'+an y = 0
называется линейным однородным уравнением n-го порядка с
постоянными коэффициентами.
Для нахождения общего решения дифференциального уравнения составляется характеристическое уравнение, которое получают заменой производных соответствующими степенями переменной k, а сама функция заменяется единицей. В зависимости от корней характеристического уравнения находится общее решение дифференциального уравнения. Если корни характеристического уравнения k1, k2 ,K действительные и не кратные,
то |
решение |
уравнения |
имеет |
вид: |
y = C1ek1x +C2ek2 x +K. |
Если корни |
|||
k1, k2 ,Kдействительные |
и |
имеют |
кратность |
|
l1, l2 ,K |
,то |
|||
y = ek1x (C0 +C1x)l1 −1 + ek2 x (D0 + D1 x)l2 −1 +K. |
Если |
корни k1, k2 ,K |
комплексные |
||||||
k1 |
= a1 ±b1i, k2 = a2 ±b2i,K, то y = ea1x ( A1 cos b1x + B1 sin b1x) +ea2 x ( A2 cos b2 x + B2 sin b2 x) +K |
||||||||
|
Дифференциальное |
уравнение |
y(n) + a1 y(n−1) + a2 y(n−2) |
+K+ an−1 y'+an y = f (x) |
|||||
называется |
линейным |
неоднородным |
уравнением |
n-го порядка |
с |
||||
38
постоянными коэффициентами. Общее решение данного уравнения может быть найдено с помощью метода вариации постоянных (метод Лагранжа). Если правая часть данного дифференциального уравнения имеет специальный вид, то общее решение определяется формулой y = yн + yо , где yо – общее решение соответствующего однородного уравнения, а yн , —
частное решение данного неоднородного уравнения, которое находится с помощью метода неопределенных коэффициентов.
Метод вариации постоянных. Если y = C1 y1 +C2 y2 +K+Cn yn общее решение однородного уравнения, то общее решение неоднородного
уравнения ищут в |
виде |
|
|
y = C1 (x) y1 +C2 (x) y2 +K+Cn (x) yn . Функции |
|||||
C1 (x),C2 (x),K,Cn (x) находят из решения системы уравнений: |
|||||||||
C′y +C′y |
2 |
+K+C′y |
n |
= 0 |
|
|
|||
|
1 1 |
2 |
|
n |
|
|
|
||
C1′y1′ +C2′y2′ +K+Cn′yn′ = 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
. |
KKKKKKKKKKKKKK |
|||||||||
|
(n−2) |
|
|
(n−2) |
|
|
(n−2) |
= 0 |
|
C1′y1 |
+C2′y2 |
+K+Cn′yn |
|
||||||
|
′ (n−1) |
|
|
′ (n−1) |
|
|
′ (n−1) |
= f (x) |
|
C1 y1 |
+C2 y2 |
+K+Cn yn |
|
||||||
Метод неопределенных коэффициентов.
Укажем возможные случаи и соответствующие им виды частных решений:
Вид правой части |
|
|
Вид, соответствующего частного |
|||||||
дифференциального уравнения |
решения yн |
|
||||||||
y(n) + a y(n−1) |
+ a |
y(n−2) +K+ a |
n−1 |
y'+a |
n |
y = f (x) |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||
f (x) = Pm (x) – полином от x, степени m |
yн = Qm (x) , |
если 0 |
не |
является |
||||||
, где m может быть равным 0. |
|
|
корнем |
характеристического |
||||||
|
|
|
|
|
|
|
уравнения, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yн = xk Qm (x) , |
если |
0 |
является |
|
|
|
|
|
|
|
корнем |
характеристического |
||
|
|
|
|
|
|
|
уравнения с кратностью k. |
|
||
|
|
|
|
|
|
|
|
|
|
|
39
f (x) = Pm (x)eax , где |
m может быть |
yн = Qm (x)eax , если a |
не |
является |
||
равным 0. |
|
корнем |
|
характеристического |
||
|
|
уравнения, |
|
|
|
|
|
|
|
|
|
|
|
|
|
yн = xk Qm (x)eax , |
если |
a |
является |
|
|
|
корнем |
|
характеристического |
||
|
|
уравнения с кратностью k. |
|
|||
|
|
|||||
f (x) = (Pm (x) cosbx + Pm (x)sin bx)eax . |
yн = (Qm (x) cos bx + Rm (x) sin bx)eax , если |
|||||
1 |
2 |
|
|
|
|
|
Пусть m – наивысшая из степеней |
a+bi |
не |
является |
корнем |
||
данных полиномов. |
|
характеристического уравнения, |
||||
|
|
|
||||
|
|
yн = xk (Qm (x) cos bx + Rm (x) sin bx)eax , |
||||
|
|
если |
a+bi |
является |
корнем |
|
|
|
характеристического |
уравнения с |
|||
|
|
кратностью k. |
|
|
|
|
|
|
|
|
|
|
|
Если правая часть дифференциального уравнения, является суммой из вышеперечисленных функций, то частное решение тоже будет суммой в соответствии с каждым слагаемым.
2.1.4. Система дифференциальных уравнений
Совокупность уравнений вида
F |
(x, y |
, y |
,K, y |
, y′, y′ |
,K, y′) = 0 |
|
|
1 |
1 |
2 |
n |
1 |
2 |
n |
|
|
|
|
|
′ |
′ |
′ |
|
F2 (x, y1, y2 ,K, yn , y1 |
, y2 |
,K, yn ) = 0 |
, |
||||
|
|
|
|
|
|
|
|
KKKKKKKKKKKKK |
|
||||||
|
(x, y1, y2 |
|
′ |
′ |
′ |
|
|
Fn |
,K, yn , y1 |
, y2 |
,K, yn ) = 0 |
|
|||
называется системой дифференциальных уравнений первого порядка.
Если система принимает вид
y′ = P |
(x) y |
+ P |
(x) y |
+K+ P |
(x) y |
+ f |
(x) |
|
||
|
1 |
11 |
1 |
12 |
2 |
1n |
n |
1 |
|
|
y2′ |
= P21 (x) y1 + P22 (x) y2 +K+ P2n (x) yn |
+ f2 (x) |
, |
|||||||
|
|
KKKKKKKKKKKKK |
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
+ fn (x) |
|
|
yn′ = Pn1 (x) y1 + Pn2 (x) y2 +K+ Pnn (x) yn |
|
|||||||||
40
то она называется линейной. Если функции f1 (x), f2 (x),K, fn (x) тождественно равны нулю, то линейная система является однородной.
Одним из способов решения системы является метод исключения неизвестных. Из уравнений последовательно исключают неизвестные функции, и система сводится к одному дифференциальному уравнению n-го порядка относительно одной неизвестной функции. (Ниже рассмотрен пример.)
41

2.2. Решение типовых примеров и задач.
Задание 1. Найти общее решение дифференциального уравнения
5xy′+ x2 y = 0 .
Решение. Данное уравнение можно представить в виде
5x dydx + x2 y = 0 или . 5 dyy + xdx = 0
Решаем данное уравнение с разделяющимися переменными
5∫dyy + ∫xdx = 0
Интегрируем и получаем общее решение
5 ln y + x2 = C .
2
Задание 2. Найти общее решение дифференциального уравнения
2x2 y′ = y2 + xy .
Решение. Разделим на x 2 правую и левую части уравнения, получим
y |
2 |
y |
. |
||
2 y′ = |
|
|
+ |
|
|
|
x |
||||
x |
|
|
|||
Делаем подстановку y = xt , тогда y′ = t + xt′ и уравнение принимает вид:
|
|
|
2(t + xt ) = t |
|
+ t |
или 2xt |
|
= t |
|
|
− t . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
′ |
2 |
|
|
|
|
|
|
|
|
|
′ |
|
|
2 |
|
|
|
|
|
|
|
|
||||
Разделим переменные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
= |
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
t(t −1) |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
2dt |
|
= ∫ |
dx |
|
или 2∫ |
|
dt |
|
− 2∫ |
dt |
|
= ∫ |
dx |
. |
|
|
||||||||||||||
|
|
t(t −1) |
|
|
|
x |
|
|
|
|
|
t −1 |
|
|
|
|
t |
|
|
x |
||||||||||||
Интегрируем и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 (ln |
|
|
|
|
|
|
)= ln |
|
|
|
|
|
|
|
или |
t −1 |
2 |
|
|
. |
||||||||||||
t − 1 |
− ln |
t |
x |
+ ln C |
|
= C |
x |
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
t |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
42

Делаем обратную замену
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
= C |
x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если есть возможность, то выражаем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− |
Cx |
|
|
|
|
|
|
|
|
|
|
||||||||
Задание |
|
|
3. |
|
Найти |
|
решение |
|
дифференциального уравнения, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5y |
|
|
|
y(1)=1. |
|||
удовлетворяющее начальным условиям : 8y′− |
|
=18x , |
||||||||||||||||||||||||||||||||
3x |
||||||||||||||||||||||||||||||||||
Решение. Разделим на 8 правую и левую части уравнения, получим |
||||||||||||||||||||||||||||||||||
y′− |
5 y |
9 |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24 |
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Делаем замену |
y = uv , тогда y |
′ |
|
|
|
′ |
|
|
′ |
и уравнение принимает вид: |
||||||||||||||||||||||||
|
|
= u v |
+ uv |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
′ |
′ |
|
|
5 uv |
|
9 |
|
|
|
|
|
|
′ |
|
′ |
|
5 |
|
v |
9 |
|
||||||||
|
|
|
|
u v |
+ uv |
− |
|
|
|
|
= |
|
x или u v + u v |
|
|
− |
|
|
|
|
= |
|
x . (*) |
|||||||||||
|
|
|
|
24 |
|
x |
4 |
|
|
|
|
|
4 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 x |
|
|||||||||||
Выражение в скобках приравниваем к нулю.
v′ − 245 vx = 0 .
Решаем его, разделяя переменные
dvv = 245 dxx .
Решаем
24∫dvv = 5∫dxx .
Интегрируем и получаем
5
24 ln v = 5ln x или v = x 24 .
Подставляем полученное в уравнение (*)
′ |
5 |
|
9 |
|
или u |
′ |
|
9 |
|
1− |
5 |
. |
24 |
|
|
|
|
24 |
|||||||
u x |
+ u 0 = |
|
x |
|
= |
|
x |
|
|
|||
4 |
|
4 |
|
|
||||||||
Решаем его, разделяя переменные
43

|
|
|
|
19 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
du = |
9 |
x |
|
|
dx . |
|
|
|
|
|
|
|||||||
|
|
|
24 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интегрируем и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
u = |
|
54 |
|
x |
|
+ С . |
|
|
|
|
|
||||||||
|
|
|
24 |
|
|
|
|
|
|||||||||||||
|
|
43 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Делаем обратную замену |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
54 |
|
43 |
|
|
|
|
|
|
|
54 |
|
2 |
|
5 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ Cx 24 . |
|||||||
y = uv = x 24 |
|
x 24 + C |
|
= |
|
x |
|
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получили
y = 54 x2 + Cx 5 .
24
43
Подставим начальные условия для того чтобы найти неопределенный коэффициент C
|
54 |
12 |
5 |
|
или C =1 − |
54 |
|
11 |
. |
||||||||
1 = |
+ C 1 |
24 |
|
= − |
|||||||||||||
43 |
43 |
43 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, искомое уравнение имеет вид: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||
|
|
|
y = |
54 |
x2 |
− |
11 |
x |
|
. |
|
|
|
|
|||
|
|
|
24 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
43 |
|
43 |
|
|
|
|
|
|
|
|||||
Задание 4. Найти общее решение дифференциального уравнения
xy′′ + y′ = 3 . |
|
|
|
|
|
|
|
|
|
Решение. |
Введем замену |
y′ = z и y′′ = z′ , исходное уравнение |
|||||||
принимает вид: |
|
|
|
|
|
|
|
|
|
xz′+ z =3 |
или |
|
xdz = (3 − z)dx . |
||||||
Разделим переменные |
|
|
|
|
|
|
|
|
|
|
|
|
dz |
= |
dx |
. |
|
||
|
|
(3 − z) |
|
|
|||||
|
|
|
|
x |
|||||
Решаем |
|
|
|
|
|
|
|
|
|
|
∫ |
|
dz |
|
= ∫ |
dx |
. |
||
|
(3 |
− z) |
|
|
|||||
|
|
|
|
|
x |
||||
Интегрируем и получаем
44
ln |
|
3 − z |
|
= −(ln |
|
x |
|
+ ln C1 ) или z = 3 − |
1 |
. |
||
|
|
|
|
|||||||||
|
|
|
|
C x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Делаем обратную замену |
|
|
|
|
||||||||
|
|
|
|
|
|
y′ = 3 − |
1 |
. |
|
|
||
|
|
|
|
|
|
C x |
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Решаем полученное дифференциальное уравнение, получаем
|
|
y = 3x − |
ln |
C2 x |
. |
|
|
|
|
||
|
|
|
C |
||
|
|
|
|
1 |
|
|
Задание |
5. Найти решение |
дифференциального уравнения |
||
y′′ + 4y′ + 3y =9x2 |
+ 24x + 6 удовлетворяющего начальным условиям y(0) = 0 , |
||||
′ |
= −2 . |
|
|
|
|
y (0) |
|
|
|
|
|
Решение. Составим характеристическое уравнение, соответствующие однородному дифференциальному уравнению y′′ + 4 y′ + 3y = 0 , оно имеет вид:
k 2 + 4k + 3 = 0 .
Оно имеет корни |
k1 = −1, k2 = −3 , поэтому общее |
уравнение |
||
соответствующего однородного уравнения |
|
|||
|
yo = C1e−x + C2 e−3x . |
|
||
Частное решение, соответствующее правой части дифференциального |
||||
уравнения следует искать в виде |
|
|||
|
|
|
= Ax2 + Bx + C . |
|
|
|
y |
|
|
Дифференцируем это |
уравнение дважды и подставим |
полученные |
||
производные в исходное уравнение
2 A + 8Ax + 4B + 3Ax2 + 3Bx + 3C = 9x2 + 24x + 6 .
Приравнивая коэффициенты, стоящие при одинаковых степенях x, получаем систему равенств
|
2 |
: |
3A = 9 |
x |
|
||
x : |
8A +3B = 24 . |
||
|
0 |
: 2A + 4B +3C = 6 |
|
x |
|
||
45
Получаем |
A = 3, |
B = 0, |
C = 0 . |
|
Следовательно, |
частное |
решение |
||||||||||||||
исходного уравнения имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3x2 . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||
Общее |
уравнение |
|
y = yo + |
|
|
|
= C1e−x + C2 e−3x + 3x2 . |
Теперь, |
используя |
||||||||||||
y |
|||||||||||||||||||||
начальные условия, найдем неопределенные коэффициенты. Имеем |
|||||||||||||||||||||
|
|
|
|
|
y′ = −C1e−x −3C2 e−3x + 6x , |
|
|
||||||||||||||
таким образом, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y(0) = C1e−0 |
+ C2 e−3 0 + 3 02 = C1 + C2 = 0 , |
|
|
||||||||||||||||
|
|
′ |
|
|
|
−0 |
−3C2 e |
−3 0 |
+ 6 0 |
= - C1 −3C2 = −2 , |
|
||||||||||
|
|
y (0) = −C1e |
|
|
|
|
|
|
|
||||||||||||
отсюда |
C1 |
= −1, |
C2 |
=1. |
Решение |
дифференциального |
уравнения, |
||||||||||||||
удовлетворяющего начальным условиям, имеет вид |
|
|
|||||||||||||||||||
|
|
|
|
|
|
y = −e−x + e−3x + 3x2 . |
|
|
|||||||||||||
Задание 6. Решить систему дифференциальных уравнений |
|
||||||||||||||||||||
|
|
|
|
|
|
|
x′ |
= 5x + 4 y |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
= |
|
2x − 2 y |
|
|
|||||||||
|
|
|
|
|
|
|
y′ |
|
|
|
|
||||||||||
Решение. С помощью метода замены переменных: |
|
|
|||||||||||||||||||
Выразим из первого уравнения |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
y = |
|
1 |
|
(x′−5x) |
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||||||
и продифференцируем его |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y′ = |
|
1 |
(x′′−5x′) , |
|
|
|||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||
подставим полученные выражения во второе уравнение системы |
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(x′−5x) , |
|
|
|
|
|
|
|
|
(x′′−5x′) = 2x − 2 |
|
|
|
|||||||||||||
|
|
|
|
4 |
4 |
|
|
||||||||||||||
приводим подобные, помножив на 4 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
′′ |
|
|
|
′ |
−18x = 0 , |
|
|
|||||||
|
|
|
|
|
|
|
x −3x |
|
|
||||||||||||
Таким образом, получили линейное однородное уравнение с постоянными коэффициентами, решаем его. Составим характеристическое
46
уравнение, соответствующие однородному дифференциальному уравнению x′′−3x′−18x = 0 , оно имеет вид:
|
|
|
|
k 2 −3k −18 = 0 . |
|
|
|
|
||||||||||
Оно имеет корни |
k1 = −3, k2 |
= 6 , |
|
|
поэтому общее уравнение |
|||||||||||||
соответствующего однородного уравнения |
|
|
|
|
|
|
|
|||||||||||
|
|
|
x = C1e−3x +C2e6 x . |
|
|
|
|
|||||||||||
Подставим полученный x в y, выраженный из первого уравнения |
||||||||||||||||||
1 |
|
−3x |
|
6 x ′ |
|
|
|
|
|
|
−3x |
|
6 x |
)) , |
||||
y = |
|
((C1e |
|
+C2e |
|
|
) −5(C1e |
|
|
+C2e |
|
|||||||
4 |
|
|
|
|
|
|
||||||||||||
Делаем преобразования и получаем |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y = −2C1e−3 x + |
1 |
C2e6 x . |
|
|
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
Общее решение системы принимает вид |
|
|
|
|
||||||||||||||
|
|
|
|
x = C1e |
−3x |
+C2e |
6 x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
6 x . |
|
|
||||||||
|
|
|
y = −2C e |
−3x |
+ |
1 |
C |
e |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решаем систему через характеристическое уравнение:
Ищем частное решение системы в виде
x = p 1 e kx , y = p 2 e kx
возьмем производные от функций и подставим в исходную систему
|
|
|
|
kx |
|
kx |
|
|
|
|
kx |
|
|
kp1e |
= 5 p1e |
+ |
4 p2 e |
, |
|||||||||
|
|
|
|||||||||||
|
kp |
2 |
ekx |
= 2 p ekx |
− 2 p |
ekx |
|
||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|||
сократим все на ekx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5 − k) p1 + 4 p2 |
= 0 |
. |
|
|||||||||
|
|
2 p1 |
− (2 + k) p2 = 0 |
|
|||||||||
|
|
|
|
|
|||||||||
Составляем характеристическое уравнение, соответствующее данной системе
47
|
5 − k |
4 |
|
= 0 , |
|
|
|||
|
2 − 2 − k |
|
|
|
или k 2 − 3k −18 = 0 , его корни k1 = −3, k2 = 6 вещественны и различны.
При k1 = −3 система принимает вид
|
8 p |
+ 4 p |
|
= 0 |
. |
|
1 |
|
2 |
= 0 |
|
|
2 p1 + p2 |
|
|
||
Пусть p1 = C1 , тогда p2 = −2C1 и искомое частное решение
x1 = C1e−3x , y1 = −2C1e−3x .
При k1 = 6 система принимает вид
|
- p |
+ 4 p |
|
= 0 |
. |
|
1 |
|
2 |
= 0 |
|
|
2 p1 −8 p2 |
|
|||
Пусть p1 = 4C2 , тогда p2 = C2 и искомое частное решение
x2 = 4C2 e6 x , y2 = C2 e6 x .
Общее решение системы принимает вид
x = C1e−3x + 4C2 e6 x |
|||
y = −2C e−3x + C |
2 |
e6 x . |
|
|
1 |
|
|
Задача 7. Найти кривую, проходящую через точку (2;1), если угловой коэффициент касательной к ней в любой ее точке вдвое больше абциссы точки касания.
Решение. Угловой коэффициент касательной равен производной функции, задающую искомую кривую. Получаем уравнение
y′ = 2x .
Ищем решение этого дифференциального уравнения. y = x2 + C .
Найдем неопределенный коэффициент: y(2) =1 . Получаем
22 + C =1,
C = −3 .
Искомая кривая имеет вид y = x2 −3 .
48
