6. Ряды

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский институт железнодорожного транспорта, филиал ИрГУПС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

практикум математика часть 2.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2725 26 27 > Следующая >>>

Пример 2. Исследовать на сходимость ряд ∑

3 2 n 7 + 3 n 2 − 1

6.1.Числовые ряды

6.1.1.Краткие сведения из теории

∞

Числовым рядом называется выражение U1 +U2 +... +Un + ... = ∑Un ,

n=1

∞

где U1 , U2 , ... , Un - числовая последовательность. Числовой ряд ∑Un на-

n=1

зывается сходящимся, если существует lim Sn = S , где Sn - частичная сум-

n→∞

ма, S - сумма ряда.

Необходимый признак сходимости знакоположительных рядов: ес-

∞

ли ряд ∑Un сходится, то предел его общего члена при n→∞ равен нулю:

n=1

lim Un =0 . Обратное утверждение неверно. Если этот предел не равен 0, то

n→∞

ряд расходится.

Достаточные признаки сходимости знакоположительных рядов. 1. Признак сравнения.

∞	∞
Если даны два ряда ∑Un (6.1) и ∑Vn (6.2), общие члены которых удовле-
n=1	n=1
творяют соотношению	Un ≤Vn , то из сходимости ряда (6.2) следует сходи-

мость ряда (6.1) и из расходимости ряда (6.1) следует расходимость ряда

(6.2).

На практике используется предельный признак сравнения.

219

Если существует lim

конечный, отличный от нуля, то оба ряда либо

n→∞ Vn

сходятся, либо расходятся одновременно.

∞

В качестве образцового ряда берут ряд Дирихле

∑Vn = ∑

, кото-

n=1

n=1 n

рый при p ≤ 1

расходится, а при

p > 1

- сходится.

2. Признак Даламбера.

∞

Un+1

Если для ряда ∑Un существует lim

= q , то при

q <1 ряд сходится,

n=1

n→∞

при

q >1 - расходится, при

q =1

- неопределенность.

3. Радикальный признак.

∞

lim n Un = q ,

Если для ряда

∑Un

существует

то при

q <1 ряд

n=1

n→∞

сходится, при

q >1 -

расходится, при

q =1 -

неопределенность.

4. Интегральный признак сходимости.

Если существует функция f(x),

для которой f(n)=Un ,

где

Un- общий член

∞

ряда

∑Un , то данный ряд и интеграл ∫ f (x)dx сходятся и расходятся од-

n=1

новременно.

Признак сходимости знакочередующегося ряда (признак Лейбница).

∞

Если члены знакочередующегося ряда ∑(−1)n+1Un удовлетворяют усло-

n=1

виям:

U1 >U2 >U3 >... >Un >...

1)	lim Un =0	,
	n→∞

то ряд сходится, его сумма положительна и не превосходит первого члена U1, то есть 0 < S <U1 .

220

n =1; 2; 3; ...

Если в знакочередующемся ряде ограничить сумму n членами, то ошибка, совершаемая при замене суммы ряда S на частичную сумму Sn ,

не превосходит абсолютной величины первого из отброшенных членов. Сходимость знакочередующегося ряда по признаку Лейбница называ-

ют условной, а ряд условносходящимся..

Если сходится ряд, составленный из абсолютных значений членов знакочередующегося ряда (знакоположительный ряд), то такой знакочередующийся ряд называют абсолютносходящимся.

6.1.2. Исследование числовых рядов

Пример 1. Исследовать на сходимость ряд

253 + 327 + 1911 + 1546 +L

Решение: Для исследования любого числового ряда по любому из признаков сходимости необходимо иметь аналитическое выражение (формулу)общего члена ряда U n . В нашем случае видна закономерность: величина числителя увеличивается на 4 в каждом последующем члене ряда. Подбираем общую формулу для числителя: 4n −1. При эта формула удов-

летворяет числители заданного ряда. Величина знаменателя увеличивается на 7 в каждом последующем члене ряда и его общий член 7n +18 .

Общий член числового ряда U n

4n −1

7n +18

Исследуем ряд по необходимому признаку:

4n −1

n 4

−

limU

= lim

≠ 0.

7n +18

n→∞

n 7

Общий член U n

не стремится к нулю при n → ∞ значит, по необходи-

мому признаку ряд расходится.

221

Решение: Проверим выполнение необходимого признака.

																4 n	7	3 −				2	+		4						4			7					2						4
																																n				4	3	−				+
					4 3n7			− 2n + 4													n6				n	7
																																							n					n7
limU n		= lim										= lim																	= lim										n	6				n7			=
limU n		= lim										= lim										3			1				= lim										3								=
n→∞			n→∞ 3 2n7 + 3n2 −1										n→∞			3 n	7	2	+			3		−	1					n→∞ 3		n		7			2	+	3				−		1
																																				3
																																							n5						n7
																						n5			n	7
																						n5			n	7
		7			7			4 3	−	2		+	4						7			7														7
		7			7			4 3	−	n	6	+	n	7					7	−		7	4		3			4		3						7		4	3							1
				−							6			7						−			4					4					−					4
= lim n 4			n		3 lim										= lim n				4			3					=				lim n				12		=				lim							=
= lim n 4			n		3 lim										= lim n												=	3			lim n				12		=	3			lim				12		7	=
n→∞						n→∞				3			1			n→∞							3		2			3		2	n→∞							3	2		n→∞				12	n	7
								3 2	+	3		−	1												2					2									2							n
								3 2	+	n5		−	n7
										n5			n7
4	3	1		4	3
=			=				0 = 0
=	2	∞	=		2		0 = 0
3	2	∞	3		2

Необходимый признак выполняется, следует продолжить исследования по достаточным признакам. Применим достаточный предельный признак сравнения. В качестве известного (образцового) ряда возьмем ряд Дирихле

∞

∑ V

∑

n =1

n =1 n p

3n7 −2n + 4

U n

2n7 +3n2 −1

4 3n7 −2n + 4

n p

lim

= lim

n→∞

3 2n7 +3n2 −1

n p

Согласно предельного признака сравнения этот предел должен быть равен числу, отличному от нуля. Вместе с тем, при n → ∞ и числитель и зна-

менатель стремятся к ∞. Имеет место неопределенность ∞∞ . Что бы этот пре-

дел был равен числу отличному от нуля необходимо, чтобы и числитель и знаменатель стремились к бесконечности (увеличивались) с одинаковой интенсивностью. Это возможно при условии, что наибольшие степени алгебраических выражений числителя и знаменателя равны, т.е.

74 + p = 73 , откуда p = 73 − 74 = 127 .

222

Тогда:

4 3n7 − 2n + 4

n p

4 3n7 − 2n + 4 12 n7

4 n7 4 3 −

12 n7

lim

= lim

n→∞ 3 2n7 + 3n2 −1

n→∞

3 2n7 + 3n2 −1

n→∞

3 n7 3 2 +

−

12 n7

lim

≠ 0.

2 n→∞ 12 n7

Предельный признак сравнения выполняется при условии, что в ряде

∞

Дирихле ∑

p =

<1. Ряд Дирихле расходится, значит и исследуемый

n=1

ряд то же расходится.

∞

8n2 −3

Пример 3. Исследовать ряд ∑arctg

n=1

7n5 + 2n3 − 4

Решение: Исследуем ряд по необходимому признаку.

limU n = lim arctg

3 8n2 −3

= arctg lim

8n2 −

7n5 + 2n3 − 4

n→∞

n→∞ 7n5 + 2n3 − 4

3 n

8 −

= arctg lim

n→∞

n 7

−

7 +

−

3 8 −

−

= arctg lim n

3 n

lim

= arctg

lim n

= arctg

lim

n→∞

n→∞ 6

n→∞

7 +

−

= arctg

= arctg0 = 0.

Необходимый признак выполняется. Продолжим исследования по достаточному предельному признаку сравнения. Обратим внимание, что

limWn = lim		3 8n2 −3	= 0	. Этот предел вычислен при исследовании ряда по
		7n5 + 2n3 − 4
n→∞	n→∞

необходимому признаку.

Напомним следствие первого замечательного предела:

lim arctgW =1.

W →0 W

223

			arctg		3 8n2 −3
В нашем случае: lim	arctgWn	= lim			7n5 + 2n3 − 4	=1.

	Wn				3 8n2 −3
n→∞		n→∞
				7n5 + 2n3 − 4

Здесь выполняются все условия достаточного предельного признака сравнения. Остается только исследовать поведение ряда с общим членом

3		8n2 −3
Wn =			.
Wn =	7n5 − 2n3 − 4		.
	7n5 − 2n3 − 4

Второй раз используем достаточный предельный признак срав-

∞

нения с применением ряда Дирихле ∑Vn = ∑

, аналогично примеру 2.

n=1

3 8n2

−3

lim

= lim

7n5 + 2n3 − 4

= lim

3 8n2

−3 n p

+ p

, p =

−

n→∞ Vn

n→∞

n→∞ 7n5 + 2n3 − 4

2 3 6

n p

8n2 −3 6 n11

n2 3 8 −

6 n11

n11

= lim

lim

≠ 0.

n→∞

7n5 + 2n3 − 4

n→∞

n5 7 +

−

7 n→∞ 6 n11

Предельный признак сравнения выполняется при условии, что в

∞

ряде Дирихле ∑

, p =

>1.

Ряд Дирихле сходится, все остальные ряды, в

n=1

том числе и исходный – сходятся.

		Пример	4.	Исследовать	на	сходимость	ряд
∑∞	71n (4n5 − 2n3 + 3)	.
n=1	(2n −1)!

Решение: Проверка выполнения необходимого признака потребует громоздких вычислений (применение формулы Стирлинга). Практически при наличии в общем члене факториала можно сразу применить признак Даламбера.

224

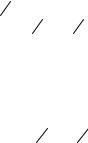
U n =

71n (4n5 − 2n3 + 3)

; U n+1 =

71n+1 (4(n +1)5 − 2(n +1)3 + 3)

(2n −1)!

(2(n +1) −1)!

(2n +1)!

71n+1 (4(n +1)5 − 2(n +1)3 + 3)

lim

U n+1

= lim

(2n +1)!

71n (4n5 − 2n3 + 3)

n→∞ U n

n→∞

(2n −1)!

(2n −1)!)

4 n 1 +

− 2 n

= lim

n→∞

71 n

4 −

(2n +1)!

4 1

−

(2n −1)!

= lim

lim

n→∞

71n

n→∞

−

n→∞

(2n +1)!

4 1+

−

(2n −1)!

4 − 2 0 +3 0

= 71

∞

lim

= 71

lim

2 3

(2n −1)! 2n(2n +1)

n→∞

4 − 2 0 +3 0 n→∞ 2n(2n +1)

4 −

∞

= 0 <1

∞

Ряд сходится.

∞ 3n − 2

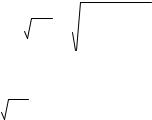
Пример 5. Исследовать на сходимость ряд ∑

n=1 3n + 4

Решение: По необходимому признаку получаем:

225

n2 lim 1+

n→∞

−

3n 1

−

−2

limU

=lim

= lim

n→∞

3n + 4

n→∞

3n 1

lim 1

n→∞

lim

−

n→∞

lim 1

n→∞

−

−∞

=0.

lim

e∞

n→∞3

lim 1+

n→∞

												3				2
										−			n		−		n
										−		2	n		−	3	n
												2				3
					1
		+			1
	limn→∞ 1
	limn→∞ 1		−			3n


=							2											=
=								3					4					=
								3					4
											n			n
									4		n		3	n
						4
				+		4

	lim 1						3n
	n→∞						3n


							4

Необходимый признак выполняется. Необходимо продолжить исследования по достаточным признакам. Из общего члена ряда легко извлечь корень n-ой степени, поэтому применим радикальный признак Каши.

3n − 2

3n − 2 n

n U n = n

3n + 4

3n − 2

3n + 4 − 6

−

lim n

U n

= lim

= lim 1

= lim 1 +

3n + 4

n→∞

n→∞ 3n + 4

n→∞

− 6

3n+4

3+4

lim

−

n→∞

3n+4

−6

3n+4

−6

lim

−

n→∞

n 3+

= lim 1 +

= e

3n + 4

3n +

n→∞

− 6

−

= e−

= e 3+

= e−2 =

<1.

∞

Ряд сходится.

226

Пример 6. Исследовать на сходимость ряд ∑∞ ln n.

n=2 n3

Решение: Необходимый признак:

limU	n	= lim	ln n

n→∞		n→∞ n3

	= lim	(ln n)′n
	= lim	(n3 )′n
	n→∞	(n3 )′n

		1		1		1
= lim		n	= lim		=		= 0.
	3n2			3n3		3 ∞
n→∞			n→∞

Применим интегральный признак:

∞

ln x

∞

U =ln x;

dU =

dx;

ln x

∞

ln x

∞

∫

dx =∫x−3 ln xdx=

+ ∫

−

dV = x

−3

dx;

V =−

;

2x2

ln x

lnb

ln2

(lnb)′b

ln2

=lim

−

=lim −

−

=−

lim

−

lim

(b2 )′b

b→∞

2x2

4x2

b→∞

2b2

4b2

2 4

2 b→∞

4 b→∞ b2

ln2

(2ln2

+1).

=−

lim

−

lim

2 b→∞ 2b

4 b→∞ b2

Несобственный интеграл сходится, значит и ряд сходится.

Пример 7. Исследовать на абсолютную и условную сходимость ряд

∑(−1)n+1	3	3n	2	− 4n + 7
∞
n=1	6 2n5 + 3n2 −9

Решение: Сходимость знакочередующегося ряда определяется по признаку Лейбница.

− 4n + 7

3 n2 3 3 −

−

3 3 −

lim

= lim

= lim n 3

lim

+ 3n

− 9

6 n5 6

2 + 3 − 9

6 2 + 3

− 9

n→∞

n→∞ 6

n→∞

1 3

3 −

3 3

= lim n−

∞

∞2

lim

0 = 0

6 2

∞

n→∞

2 +

−

2 n→∞

6 n

∞3

∞5

Признак Лейбница выполняется, ряд сходится условно.

227

Исследуем ряд на абсолютную сходимость по предельному признаку сравнения:

										3	3n2				− 4n + 7
lim	Un			= lim						6	2n5 +3n2									−9	= lim			3 3n2	−4n +7 n p						=		2		+ p =				5	, p =					5	−		2	=	1						=
										6

																																3
n→∞		Vn				n→∞										1						n←∞		6 2n5 +3n2 −9								3						6							6 3 6
3						2									n p						6	n 3 n2 3 3 −					4	+		7					1		2					5					3 3 −					4	+			7
																6											4			7																						4				7
			3n				−4n +7										n										n			2											−											n				2
																														2											−															2
																														n				n	6	n	3	n				6													n
= lim																			= lim												=lim													lim														=
= lim			6					5				2							= lim												=lim													lim														=
n→∞			6		2n			5	+3n			2	−9							n→∞						3			9		n→∞												n→∞								3						9
																						6 n5 6 2			+	3	−		9																6 2				+		3			−			9
																						6 n5 6 2			+	n3	−		n5																6 2				+		n3			−			n5
																										n3			n5																						n3						n5
				1		2		5	3 3 −						4		+			7		3
				1	+	2	−	5							∞		+			2			3
					+		−													2
= lim n6						3		6											∞		=			≠0.
= lim n6						3		6													=	6		≠0.
n→∞																3				9		6	2
									6		2 +					3		−		9			2
									6		2 +			∞3				−		∞5
														∞3						∞5

Выполнение условий предельного признака сравнения происходит при сравнении с расходящимся рядом Дирихле ( p = 16 <1) значит, знакочередую-

щийся ряд абсолютно расходится, но является условно сходящимся. ЗАМЕЧАНИЕ. Исследование знакочередующегося ряда, содержащего в

общем члене факториал, по признаку Лейбница усложнено вычислением предела факториала (нужно использовать формулу Стирлинга). В этом случае можно сразу исследовать ряд на абсолютную сходимость и, если она имеет место, то исследование завершается, т.к. абсолютно сходящийся ряд сходится условно и подавно.

6.2.Функциональные ряды

6.2.1.Краткие сведения из теории

∞

Область сходимости функционального ряда ∑Un (x) , где Un(x),

n=1

n=1,2,3… - функции одной переменой, есть совокупность значений переменной x, при которых ряд сходится. Сумма ряда в области сходимости являет-

228

∞

ся некоторой функцией от x : f (x) = ∑Un (x) , для x из области сходи-

n=1

мости.

Область сходимости определяется решением неравенства на основе достаточных признаков Даламбера или радикального признака :


lim	Un+1		(x)	<1;	lim n	Un (x)	< 1.
	Un+1		(x)
		Un (x)
n→∞		Un (x)			n→∞

Принадлежность концов интервала к области сходимости определяется на основе исследования числовых рядов, получающихся после подстановки значений этих концов в функциональный ряд.

В частном случае, если функциональный ряд представляет собой

∞

степенной ряд вида ∑an (x − x0 )n , область сходимости по приведен-

n=0

ным формулам определяется:

lim

= lim n

(x − x

x − x

lim n

, или

x − x

n→∞

lim n

R – радиус

n→∞

Здесь

R = lim

R =

где

сходимости .

an+1

n→∞

lim n

n→∞

Интервал сходимости получается в результате решения неравенства:

x − x0 R; x0 − R x x0 + R.

229

Если функция f(x) в точке а непрерывна вместе со своими производными, то в окрестности точки x=a справедлива формула (ряд) Тейлора:

∞

(n)

(a)

f (x)= ∑

(x − a)n =

n=0

= f (a) + f / (a)(x − a) +

f // (a)

(x − a)2

f /// (a)

(x − a)3 +K

f (n) (a)

(x − a)n +K .

При

a=0 ряд Тейлора преобразуется в ряд Маклорена :

∞

(n)

(0)

///

(0)

(n)

(0)

f (x)= ∑

xn =f (0) + f / (0)x +

2 +

+K+

xn +K .

n=0

Таблица рядов Маклорена для некоторых функций.

∞

ex = 1

+ x

+K+

+K= ∑

(−∞ < x < ∞) ;

n=0

2n+1

∞

2n+1

sin x = x −

−

+K+ (−1)n

+K= ∑(−1)n

(2n + 1)!

n=0

(−∞ < x < ∞) ;

∞

cos x = 1

−

+K+ (−1)n

+K=

∑(−1)n

(2n)!

n=0

(−∞ < x < ∞) ;

(1 + x)

= 1 + mx +

m(m −1)

m(m −1)(m − 2)

+K+

m(m −1)(m − 2)K(m − n + 1)

∞

−1)K(m − n + 1)

xn +K= ∑

m(m

n=0

(−1 < x ≤1) ;

230

n+1

∞

n+1

ln(1

+ x) = x −

−

+K+ (−1)n

+K= ∑(−1)n

(n + 1)

n=0

(−1 < x ≤1) ;

2n+1

∞

2n+1

arctg x = x −

−

+K+ (−1)n

+K= ∑(−1)n

2n + 1

n=0

(−1 < x ≤1) ;

2n+1

∞

2n+1

sh x =

+K+

+K= ∑

(−∞ < x < ∞) ;

(2n + 1)!

n=0

∞

ch x = 1 +

+K+

+K= ∑

(−∞ < x < ∞) .

(2n)!

n=0

В скобках указаны интервалы сходимости рядов.

Разложение функций в ряд Тейлора позволяет с любой степенью точности приближенно вычислить значение функции в точке, пределы, определенный интеграл, найти частное решение дифференциального уравнения (задачу Коши) и другие.

6.2.2 Решение типовых примеров с использованием функциональ-

ных рядов.

∞	(x + 2)	n
Пример 8. Найти область сходимости ряда ∑	(x + 2)			.
Пример 8. Найти область сходимости ряда ∑	(3n − 2)5		n	.
n=1	(3n − 2)5

231

Решение: Для определения области сходимости функционального ряда используем признак Даламбера числового ряда, при этом предел вычисляется

от выражений функционального ряда взятых по модулю: lim

U n+1 (x)

<1.

U n (x)

n→∞

lim

U n+1 (x)

= lim

+ 2)n+1 (3n − 2)5n

= lim

lim

3n − 2

lim

(x + 2)n+1

U n (x)

(3(n +1)− 2)5n+1 (x

+ 2)n

5n+1

3n +1

(x + 2)n

n→∞

n 3

−

(x + 2)n (x + 2)

lim

x + 2

<1.

(x + 2)n

5 n→∞

n→∞

n 3

x + 2

< 5;

-5 < x + 2 < 5;

−5 − 2 < x < 5 − 2;

− 7 < x < 3.

Тот же результат можно получить по приведенной ранее формуле для радиуса сходимости (но только для этого ряда).

1			1		1
an =		;	an+1 =		=		.
	(3n − 2)5n			[3(n +1)− 2]5n+1		(3n +1)5n+1


R = lim			a	n	= lim	(3n +1)5n+1
			a	n		(3n +1)5n+1
			an+1			(3n − 2)5n
	n→∞		an+1		n→∞	(3n − 2)5n
	x + 2	< 5;			− 7 < x < 3.
	x + 2	< 5;			− 7 < x < 3.

				1
	n	3	+			5n 5
	n	3	+	n
= lim				n	lim		= 5.
= lim				2	lim	5n	= 5.
n→∞				2	n→∞	5n
	n	3	−
	n	3	−	n
				n

Исследуем ряд на концах найденного интервала сходимости (подставляем значение концов интервала в функциональный ряд).

∞	(− 7	n	∞	5	n		∞	1
x = −7; ∑		+ 2)	= ∑(−1)n				= ∑(−1)n		.
		n		(3n − 2)5		n		3n − 2
n=1	(3n − 2)5		n=1				n=1

Этот знакочередующийся ряд сходится по признаку Лейбница:

lim	U n	= lim	1	=	1	= 0.

			3n − 2		∞
n→∞		n→∞

Значит конец интервала (точка) x = −7 входит в область сходимости ря-

да.

∞	(3 + 2)	n		∞	1
x = 3; ∑				= ∑		.
	(3n − 2)5		n		3n − 2
n=1				n=1

232

Данный числовой ряд с положительными членами расходится по признаку сравнения:

	U n			1			n p
lim		= lim	3n − 2			= lim		=
							3n − 2
n→∞ Vn		n←∞			1	n→∞

n p

p =1	= lim		n		=
			n
				2
	n→∞
	n→∞
		n 3	−
		n 3	−	n
				n

1		=	1	≠ 0.
3 −	2	=	3	≠ 0.
	2		3
	∞

∞	1
(ряд Дирихле ∑		при	p =1 расходится).
	p
n=1	n

Значит конец интервала x = 3 не входит в область сходимости ряда. Окончательный ответ: −7 ≤ x < 3.

Пример 9. Найти область сходимости ряда

∞

4n3 − 2n + 3

∑

2n3 + n

n=1

2 −3(3x2 +10x + 9)

Решение: Методика решения как в примере 8.

4(n +1)3 − 2(n +1)+ 3

lim

U n+1

(x)

= lim

2(n +1)3 + (n +1)2 − 3(3x 2 +10x + 9)n+1

U n (x)

4n3 − 2n + 3

n→∞

2n3 + n 2 − 3(3x 2 +10x + 9)n

(4(n +1)3 − 2(n +1)+ 3)

2n3

+ n 2 − 3(3x 2 +10x + 9)n

4(n +1)3

− 2(n +1)+ 3

= lim

(4n3 − 2n + 3) 2(n +1)3 + (n +1)2 − 3(3x 2 +10x + 9)n+1

4n3 − 2n + 3

n→∞

→∞

× lim

2n3 + n

2 − 3

lim

(3x 2 +10x + 9)n

2(n +1)3 + (n +1)2 − 3

(3x 2 +10x + 9)n (3x 2 +10x + 9)

n→∞

4 1

−

2 +

−

= lim

lim

n→∞

−

n→∞

n 2 1 +

233

1 3

−

1 3

4 1

∞2

∞3

2 +

∞ − ∞3

×lim

∞

n→∞

3x2 +10x

−

∞

∞3

2 1

∞

<1.

3x2 +10x +9

Трехчлен

3x2

+10x + 9

имеет

дискриминант

D =100 − 4 3 9 =100 −108 = −8 < 0 .

Т.к. коэффициент при x 2 равен 3 > 0 ,то этот трехчлен при любом x положительный, значит модуль можно опустить и остается решить неравенст-

во:

<1.

3x2 +10x + 9

−1

< 0;

1 −3x2

−10x −9

< 0;

−3x2

−10x −8

< 0;

3x 2 +10x +8

> 0.

3x2 +10x + 9

3x2 +10x

+ 9

3x2 +10x + 9

Т.к. знаменатель при любом x положительный, остается решить нера-

венство: 3x

+10x

+ 8

> 0. ; 3(x +

2) x

>0. Методом интервалов рис.6.1:

-2

−

Рис.6.1

Получаем два интервала сходимости: x < −2; x > −

Исследуем поведение функционального ряда на концах интервала сходимости.

При подстановке в функциональный ряд значений обоих концов интер-

∞	4n	3	− 2n	+ 3
валов образуется один и тот же числовой ряд ∑					.

n=1	2n3 + n2 −3

Действительно: (3x2 +10x + 9) x=−2 = 3(−2)2 +10(−2) + 9 =1;

234

(3x	2	+10x + 9)					4	2			4	+ 9	=1.

				4	= 3	−			+10	−
							3				3
			x=−
				3

Этот числовой ряд расходится по необходимому признаку:

4 −

− 2n

+ 3

4 −

∞2

∞3

limU n = lim

= lim

= ∞.

+ n

−3

2 + 2

− 3

2 +

2 −

n→∞

∞3 ∞4 ∞6

Значит, концы интервалов не входят в интервалы сходимости.

Окончательно

область

сходимости

исследуемого

ряда:

x(− ∞;−2) − 4 ;+∞ .

Пример 10. Найти область сходимости ряда

∑7 4n23n −3 sin 2n x.

Решение: Область сходимости определяем по методике примера 8.

Un+1 (x)

2n+1 sin2(n+1)

lim

= lim

4(n +1)3 −3

= lim

2n+1 sin2n+2 x 7

4n3 −3

Un (x)

2n sin2n x

2n sin2n x 7

4(n +1)3 −3

n→∞

7 4n3 −3

2n 2

sin2n x sin2 x

n3 7

4 −

= lim

lim

= 2

sin2 x

<1.

n→∞

sin2n x

n→∞

−

4 1

sin

2 x

;

sin x

;

−

< sin x <

;

−

+ kπ < x <

+ kπ, k = 0,±1,±2,K

Исследуем ряд на концах интервала сходимости.

Подставим значения обоих концов интервала в выражение sin 2n x :

	2n		2	n						1	2	n		1
	2n		2	n						1	2	n		1
sin		x = (sin		x)				=	±				=			.
sin		x = (sin		x)				=	±				=			.
					x=±	π	+kπ			2				2	n
						4				2				2

Это значит, на концах интервала сходимости исходный функциональный ряд становится одним и тем же числовым рядом.

235

∞

∑

n=1 7 4n3 −3

Исследуем на сходимость этот ряд.

Необходимый признак limU n

= lim

= 0 выполняется.

n→∞

n→∞ 7 4n3 −3

∞

По признаку сравнения

U n

7 4n3

−3

n p

p =

7 n3

ряд

lim

= lim

≠ 0

n→∞

−3

n→∞

7 n3 7 4 − 3

∞

расходится,

т.к. ряд Дирихле ∑

при

p =

расходится.

Значит концы

n=1

интервала

не

входят в

область

сходимости.

Область сходимости

ряда

− π

+ kπ < x <

+ kπ, k = 0,±1,±2,K.

Аналитическое решение поясняется графиком (рис.6.2):

0,7 sin x sin 2 x

0,5

− π 2

− π 4

π 4

π 2

Рис.6.2

Замечание. Последний пример показывает, что для его решения требуется уметь решать тригонометрические неравенства. В заданиях на контрольные работы встретятся примеры, при решении которых потребуется так же решать логарифмические и показательные неравенства.

Пример 11. Вычислить интеграл

236

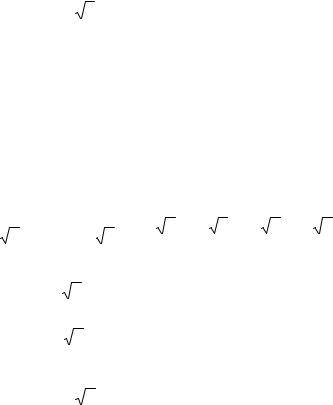
0,5		− cos x
∫	1		dx с точностью ε=0,001.

0		x

Решение: Используем разложение косинуса в ряд Маклорена:

cosU =

1 −

U 2

U 4

−

U 6

−L.

В нашем случае

U = x. Тогда cos

x =1−

(

x )2

( x )4

−

( x )6

(

x )8

+L=1−

−

−L.

1 − cos

x =1 −1 +

−

+L. =

−

+L.

1 − cos

−

+L.

0,5

− cos x

0,5

∫

dx = ∫

−

+L dx

−

4 8!

0,5

−

0,52

0,53

−

0,54

+L= 0,25 − 0,0052 + 0,000058 −L≈ 0,25 − 0,0052 = 0,2448.

2 4!

3 6!

Для обеспечения заданной точности ε = 0,001 достаточно взять два пер-

вых члена ряда. Третий член ряда по абсолютной величине < ε , и начиная с этого члена и далее, ряд можно отбросить. Этот расчет основан на свойстве знакочередующегося ряда: при замене суммы ряда частичной суммой происходит ошибка не превышающая по абсолютной величине значения первого из отброшенных членов.

Замечание. Если при вычислениях степенной ряд окажется знакопостоянным, то обеспечение заданной точности вычислений нужно производить

по оценке остаточного члена в форме Лагранжа: Rn (x) =						(x − a)n+1	f (n+1)(ξ), кото-
по оценке остаточного члена в форме Лагранжа: Rn (x) =						(n +1)!	f (n+1)(ξ), кото-
						(n +1)!
рый позволит выбрать необходимое число членов ряда n .
Пример 12. С помощью рядов решить дифференциальное уравнение:
y	′′	+ xy	′	+ y = 0; y(0) = 0,	′
y		+ xy		+ y = 0; y(0) = 0,	y (0) =1.

237

Решение: Решение ДУ находится в виде ряда Тейлора (Маклорена):

y(x) = y(a) +	y′(a)	(x − a) +	y′′(a)	(x − a)2	+L+	y(n) (a)	(x − a)n +L,
	1!		2!			n!

где точка x = a определяется из начальных условий (в приведенном примере

a = 0 )

Значения функции и её производных для ряда Тейлора находятся из начальных условий непосредственно для первых членов и для остальных членов ряда путем последовательного дифференцирования исходного ДУ, разрешенного относительно старшей производной и вычисленной в точке x = a . Для тех значений x , для которых получившийся ряд сходится, он представляет решение ДУ:

y(a) = y(0) = 0;

′

y (a) = y (0) =1;

y′′ = −xy′− y;

)

′′′

′ ′

+ xy

′′

− y

′

= −y

′

− xy

′′

− y

′

= −2 y

′

′′

= −(x y

− xy ;

(4)

= −2 y

′′

− y

′′

− xy

′′′

= −3y

′′

′′′

− xy ;

y(5)

= −3y′′′ − y′′′− xy(4) = −4 y′′′− xy(4);

y(6) = −4 y(4) − y(4) − xy(5) = −5y(4) − xy(5);

y(7 ) = −5y(5) − y(5) − xy(6) = −6 y(5) − xy(6);

y ′′(0 ) = 0; y ′′′(0 ) = −2; y (4 )(0 ) = 0;

y (5 )(0 ) = 2 4;

y(6)(0) = 0;

y(7 )(0) = −2 4 6.

Видна закономерность:

y(n) = −(n −1) y(n−2) − xy(n−1);

y(2n)(0) = 0; y(2n+1)(0) = (−1)n 2 4 6 L 2n.

Подставим все значения в ряд:

y(x) =0 +

x +

x2 −

x3 +

x4 +

2 4

x5 +

−

2 4 6

x7 +L+

(−1)

2 4 6 L 2n

x(2n+1)

(2n +1)!

Выполним преобразования:

y(x) = x −

2 4

x5 −

2 4 6

x7 +L+(−1)

2 4 6 L 2n

x2n+1

1 2 3

1 2

3 4 5

1 2 3 4 5 6 7

1 2 3 L 2n(2n +1)

y(x) = x −

−

+L+ (−1)n

x2n+1

3 5

1 3 5 7

1 3 5 L (2n +1)

1 3

Определим радиус сходимости этого ряда:

238

an =

;

an+1 =

1 3

5 L (2n +1)

1 3 5

L (2n +1)(2n + 3)

1 3 5 L (2n +1)(2n + 3)

= lim(2n + 3)

R = lim

= lim

= ∞

an+1

1 3 5 L (2n +1)

n→∞

Полученое решение ДУ справедливо для всех x .

6.3. Ряды Фурье и интегралы Фурье 6.3.1. Краткие сведения з теории

Если на интервале [-π,π] функция f(t) удовлетворяет условию Дирихле: функция непрерывна с конечным числом экстремумов или имеет конечное число точек разрыва первого рода - то ряд Фурье этой функции сходится в точках непрерывности к самой функции f(t), а в точках разрыва первого рода - к полусумме левого и правого пределов функции f(t).

∞

f (t) =

+ ∑(an cos nt + bn sin nt) ,

где

n=1,2,3,…

n=1

a0 =

∫

f (t)dt ;

an =

∫

f (t)cos ntdt ;

bn =

∫

f (t)sin ntdt .

−π

Если функция

f(t)

периодична с периодом

2π,

удовлетворяет усло-

вию Дирихле на этом перигде,

то ряд

Фурье данной

функции сходится

ней

для любого t.

То же самое относится и к

случаям,

если функция

f(t).периодична с периодом

или

2l. Соответствующие формулы имеют

вид:

∞

2π nt + bn sin

2π nt) ,

f (t) =

+ ∑(an cos

n=1

2π

где

a =

∫

f (t)dt ;

∫

f (t)cos

ntdt ;b =

∫

f (t)sin

ntdt

−

239

∞

π nt + bn sin

π nt) ,

f (t) =

+ ∑(an cos

n=1

где a =

1 l

f (t)dt ;

1 l f (t)cos π ntdt ;

= 1 l f (t)sin π ntdt .

l ∫

−l

Если функция

f(t)

четная, то

bn = 0 ;

если нечетная

a0 = an = 0 и

ряд Фурье упрощается.

Если

f(t) задана на полуинтервале, то ее можно разложить в ряд Фу-

рье по косинусам или синусам, продлив функцию соответственно четным или нечетным образом на весь период.

Иинтегралом Фурье представляется функция f (x) непериодическая, к ко-

торой предъявляются два условия:

1)должна быть кусочно-гладкая, т.е. должна быть на некотором интервале непрерывной и иметь непрерывную производную во всех точках этого интервала , за исключением, быть может, конечного числа точек, в которых функция имеет разрыв 1 рода (это аналог условия Дирихле);

2)должна быть абсолютно интегрируема на всей числовой оси, т.е.

∞

должен быть сходящимся ∫ f (x) dx = A ≠ ∞. На электротехническом языке

−∞

это означает одиночный импульс тока или напряжения, имеющий начало и конец.

Тогда функция f (x)					представляется несколькими видами интеграла
Фурье:
			∞	[A(α)cos				αx] dα,
а)	f (x) = ∫			[A(α)cos	αx + B(α)sin			αx] dα,
			0
		1	∞			1		∞
где	A(α) =	1	∫ f (t)cos α t dt, B(α)			1		∫ f (t)sin α t dt .
где	A(α) =	π	∫ f (t)cos α t dt, B(α)			π		∫ f (t)sin α t dt .
			∞				−∞

240

Здесь

f (x) и

f (t)

- одна и та же функция с аргументами x и

t. В

частных случаях

f (x) может быть четной и нечетной.

Если f (x)

- чётная, то B(α) =0,

тогда

∞

f (x) = ∫A(α)cosα x

dx ,

где

A(α) =

∫ f (t)cos

α t dt .

∞

Иногда вводят функцию F (α) =

∫ f (t)cos α t dt,

∞

тогда

f (x) =

∫F (α)cos α

dα.

В этом случае функцию F(α)

назы-

вают

косинуспреобразованием Фурье.

Если f (x)

- -нечетная, то A(α) =0

и тогда

∞

f (x) = ∫B(α)sin

α x

dα ;

B(α) =

∫ f (t)sin α tdt.

Если ввести функцию

∞

Φ(α) =

∫ f (t)sinα tdt

синус-преобразование

Фурье,

∞

то

f (x) =

∫Φ(α)sinα

x dα. .

b) Второй вид интеграла Фурье :

	1	∞	∞
f (x) =	1	∫dα ∫ f (t) cos α (t − x) dt .
f (x) =	π	∫dα ∫ f (t) cos α (t − x) dt .
0			−∞
с) Третий вид интеграла Фурье – в комплексной форме – здесь не рас-
сматривается.
Представить функцию f (x)				интегралом Фурье значит:
Вид а) -			найти функцию	A(α) и B(α) или F (α) или Φ(α) и под-

ставить в соответствующую формулу.

241

∞

Вид b) - посчитать внутренний интеграл ∫ f (t)cosα(t − x)dt и под-

−∞

ставить в формулу.

6.3.2. Решение типовых примеров с использованием рядов и интеграла Фурье

Пример 13. Разложить функцию f (t) = 2t в ряд Фурье на интервале(-

π,π).

Решение. Продолжим функцию периодическим образом с периодом

2π ( рис. 6.3. ).

f(t)

π/2

-π

-π/2

Рис. 6.3.

Функция

f (t) =

нечетная, поэтому коэффициенты

= a

=0 .

U = t;

dV = sin ntdt

bn =

∫

f (t)sin ntdt =

∫

sin ntdt =

dU = dt; V = − 1 cos nt

−π

−

cos nt

∫

cos ntdt

−

cos nπ +

sin nt

= − n1 cos nπ = n1 (−1)(−1)n = n1 (−1)n+1

242

∞

1 sin nt =sin t

− sin 2t

+ sin 3t

− sin 4t +K .

Ряд Фурье:

= ∑(−1)n+1

n=1

Равенство справедливо всюду, кроме точек разрыва (на концах интер-

вала), где ряд сходится к

0 , т.к. сумма ряда равна :

lim

π − π

t→(2π +1)−0

t→(2π −1)+0

2 2

= 0 .

Пример 14 . Разложить в

ряд Фурье

функцию

на

f (t) =

−1

интервале (π,π).

Решение. Продолжим функцию периодическим образом с периодом

2π (рис.6.4.)

f(t)

-3π -2π -π π 2π 3π t

-1

Рис. 6.4.

Функция

f (t) =

−1

четная,

поэтому

коэффициент

=0 .

π 3

π 2

a0 =

∫

f (t)dt =

∫ 3

−1 dt =

− t

−π

= 2

−1

−π

243

2 t2

2 π

U = t;

dV = sin ntdt

−1

sin nt

−

∫

t sin ntdt

V = −

dU = dt;

cos nt

4π

∫

(−1)n .

= −

−

cos nt

cos ntdt

cos nπ −

sin nt

3nπ

3n π

Ряд Фурье:

∞

π 2

cost

cos 2t

cos 3t

−1

+ ∑

(−1)n cos nt =

−1 −

−

−K .

n=1

Пример 15.

Разложить в ряд Фурье функцию

f (t) =

, −π ≤ t

≤0

2t,0 < t ≤

Решение. Продолжим функцию периодическим способом с периодом

2π (рис. 6.5.)

f(t)
	2π
	π
-2π -π		π	2π 3π	t
	-π			t
	-π
	Рис.6.5.

244

1 π

1 0

1 π 2

∫

∫ tdt + ∫2tdt =

a0 = π

f (t)dt =π

+ t

0 =

− 2 +π

−π

2t cos ntdt

U = t;

dV = cos ntdt

∫

f (t)cos ntdt =

∫

t cos ntdt +

∫

−π

dU = dt;

V = n sin nt

sin nt

cos nt

sin nt

cos nt

−π

−

cos nπ

cos nπ −

(

1 − (−1)n )+

((−1)n

−1)

π n

(1 − (−1)n − 2 + 2(−1)n ) =

((−1)n −1) =

0,n = 2k

a2k+1

= −

;k=0,1,2,…

;n = 2k + 1

+ 1)2

−

π(2k

πn

U = t; dV = sin ntdt

∫

π −π

f (t)sin ntdt =

t sin ntdt

2t sin ntdt

−π

dU = dt; V = − n cos nt

cos nt

sin nt

cos nt

sin nt

−

−π

−

cos nπ −

2π

cos nπ

3π

(−1)n+1

Ряд Фурье:

245

∞

f (t) =

+ ∑

−

cos(2k

1)t

+ ∑

(−1)n+1 sin nt =

π(2k + 1)

k=0

n=1 n

cost

cos 3t

cos 5t

sin t

sin 2t

sin 3t

−

+ 3

−

−K .

Пример 16.	Разложить функцию f (t) = t на интервале	(0 ;π) в ряд
косинусов.
Решение.	Чтобы в разложении были только косинусы,	необходимо
иметь четную функцию, поэтому продолжим функцию f (t) = t		на интерва-

ле (0 ;π) четным, периодическим образом ( рис. 6.6.) .

f(t)

−3π

−2π

−π

2π

Рис. 6.6.

2 π

(π 2

π 2

f (t)dt =

t dt =

− 0) =

=π

∫0

π ∫0

246

U = t

dV = cos

t dt

an =

f (t)cos n

t dt =

t cos

t dt =

∫0

dU = dt

V = n sin

n t

sin

−

∫

sin n

dt =

cos

n t

(cos nπ − cos0) =

πn

−

, n =

2k −1,

k =1, 2,3,...

(−1)

−1

(2k −

πn2

= 2k

bn = 0

∞

cost

cos 3t

cos 5t

f (t) = t

+ ∑

−

cos(2k

−1)t =

−

+...

π(2k −1)

k=1

Чтобы разложить ту же функцию f (t) = t на интервале (0,π) в ряд си-

нусов, нужно продолжить эту функцию нечетным, периодическим образом

(рис.6.7.).

		f(t)
-3π	-2π -π	π
		π
		π	2π	3π	t
		-π			t

Рис. 6.7.

а0 = аn =0

∫

∫ t sin n t

bn =

f (t)sin

n t dt =

dt =

(−

cos nt +

sin nt)

= −π2n π cos nπ = − 2n (−1)n = 2n (−1)n+1 .

247

∞	∞			nt = 2(sin t	− sin 2t	+ sin 3t	− sin 4t
f (t) = t = ∑bn sin	nt =∑2		(−1)n+1 sin	nt = 2(sin t	− sin 2t	+ sin 3t	− sin 4t	+...) .
n=1	.	n		1	2	3	4
	n=8

Еще раз обратим внимание на то, что указанные в примерах функции раскладываются в соответствующий ряд Фурье только в указанных интервалах (в одном периоде). За пределами интервалов этого разложения нет.

Если интервалы заданы (−T	, T ) или (−l,l) , то разложение в ряд
2	2

Фурье производят по приведенным выше формулам.

Пример 17. Найти косинус-преобразование Фурье и написать интеграл

cos

2x,

≤

Фурье для функции:

(рис.6.8).

f (x) =

Решение.

Построим график функции (рис. 6.8.)

f(x)

-π/2

-π/4

π/4

π/2

-1

Рис.6.8.

Проверим функцию

f(x)

на абсолютную интегрируемость:

∞

π / 2

cos

2x dx =

sin

π / 2

π − sin

∫

f (x)

dx = ∫

−π / 2

2 (sin

(−π ))= 0 .

−∞

−π / 2

Несобственный интеграл существует, значит f(x) абсолютно интегрируема на всей числовой оси.

Найдем косинус-преобразование :

248

∞

π / 2

∞

F (α) =

∫ f (t)cosαtdt =

∫ cos 2t cosαtdt

∫

0 cosαtdt =

π / 2

∫

21 [cos t(2 −α) + cos

t(2 +α)]dt =

sin t(2 −

sin t(2 +

π / 2

α) +

α)

2π

−α

2 +α

sin(π −

πα ) +

sin(π +

πα ) =

2π

−α

2π

2 +α

sin

πα

−

sin

πα =

2π

−α

2π

+α

πα

2α sin

πα

sin

−

sin

2π

2 +α

2π (4 −α2 )

−α2

2 2 −

Интеграл Фурье для функции:

∞

sin λα cosαxdα =

f (x) =

∫F

(α)cosαxdα =

∫

4 −α

∞

sin λα cosαxdα .

∫

4 −α

6.4.Задания на контрольную работу

Задание 1 . Исследовать на сходимость числовые ряды (для знакочередующихся рядов провести исследование на абсолютную и условную сходимость).

	1	+ 3 + 5		7		∞	3 n −1
а)			+		+K	б) ∑sin
	3						n5 + 2n2 − 3

		6 9	12			n=1

249

в) ∑∞ 2n3 − n

n=1 2n

д) ∑∞ ln3 n

n=1 n

а)	2 + 6			+		10		+	14	+K
	6	9				12			15
в)	∞	3	n	(4n			2	−1)
в)	∑	3		(4n				−1)
	n=1			(n		+ 1)!
	n=1
	∞	3	ln		2	n
д)	∑		ln			n
д)	∑			n
	n=1			n
	n=1

а) 62 + 78 + 1012 + 1712 +K

в) ∑∞ 3n+1 (4n4 + 2n2 −1) n=1 (3n)!

д) ∑∞ 3 ln2 n

n=1 n

а)	1	+	7		+ 13 +	20	+K
	10		14			22
					18
	∞	(4n		2	− 2n +	1)3	n
в) ∑
	n=1			(3n − 1)!

∞	3n −1	n2
г) ∑	3n + 2
n=1	3n + 2
∞		32n
е) ∑(−1)n+1
е) ∑(−1)n+1		(n + 2)!(2n −1)
n=1		(n + 2)!(2n −1)
n=1

б)
∞	7n + 3	n2
г) ∑	7n −1
n=1	7n −1

∞	4n + 5	3n+5
е) ∑(−1)n+1	3n + 1
n=1	3n + 1

∞		4n − 3
б) ∑
	(2n	+ 1) n + 3
n=1

∑∞ 2n2 + 1 n2

г) n=1 n2 + 1

∞	n	3	4	n
е) ∑(−1)n+1
	(n	+ 3)!
n=1


	∞			2	+ 2n
б)	∑	n
				n5 + 4
	n=1
г)	∞		9n			+7	n
	∑		9n			− 3
	n=1

250

д) ∑∞ 1

n=2 nln9 n

а) 64 + 109 + 1612 + 1522 +K

в) ∑∞ (2n −1)!(2n3 −1)

n=1 10n

д) ∑∞ 5 ln6 n

n=2 n

а)	6 +		9	+ 12 +	15		+K
а)	6 +		11	+ 12 +	15		+K
	9		11	13	15
	∞		(3n −1)!11n
в)	∑
в)	∑	(3n		+ 1)!(6n		3	+ n)
	n=1	(3n		+ 1)!(6n			+ n)
	∞			1
д)	∑			1
д)	∑		n	3 ln4 n
	n=2		n	3 ln4 n

а)

в)

∞

(6n)!(3n5 − n3 )

∑

n=1

∞

д)

∑

n=2

∞	5n − 6	3n+4
е) ∑(−1)n+1
е) ∑(−1)n+1	3n + 14
n=1	3n + 14

∞	n	2	+ 2n
б) ∑
	n5 + 4 (n −1)
n=1

г) ∑∞ (n + 4)n n=1 (n + 5)!

∞	(n + 4)6	n
е) ∑(−1)n+1	(n + 4)6
е) ∑(−1)n+1	(n +7)!
n=1	(n +7)!
n=1

∞	5		10	+1
б) ∑		n
	(5n	3
n=1		+ 4n) n

∑∞ 4n + 12 n2

г) n=1 4n + 9

∞	8n − 5	3n
е) ∑(−1)n+1	6n + 8
n=1	6n + 8

∞	3 9n + 1
б) ∑	3 9n + 1
б) ∑	n5 + n3
n=1	n5 + n3
∞	(n +n+34 )!
г) ∑	(n +n+34 )!
n=1	n
∞		n
е) ∑(−1)n+1 9			(2n	+ 5)
n=1		(n + 3)!
n=1

251

а) 142 + 1911 + 2420 + 2929 +K

	∞					6 n (3n −1)!
в)	∑
в)	∑		(3n		+ 1)!(2n		4	− 3n	2	)
	n=1		(3n		+ 1)!(2n			− 3n		)
	∞	5		ln	7	n
д)	∑			ln		n
д)	∑			n
	n=1			n
	n=1

а) 93 + 1611 + 1923 + 2730 +K

∞	n	7			2
в) ∑	41	(5n	+ n			−1)
n=1		(4n − 3)!
n=1
∞		1
д) ∑		1
д) ∑	(n + 1)ln		4	(n + 1)
n=1	(n + 1)ln			(n + 1)

10.

а) 71 + 114 + 157 + 1019 +K

	∞			(3n − 2)!5n
в)	∑
в)	∑	(3n)!(2n			5	− 3n	+ 1)
	n=1	(3n)!(2n				− 3n	+ 1)
	∞		4	(n + 1)
д)	∑ln			(n + 1)
	n=1		n + 1
	n=1

	∞		n + 4
б)	∑		n + 4
б)	∑	(2n + 1) n3 + 1
	n=1	(2n + 1) n3 + 1
г)	∞		7n − 2	n2
г)	∑		7n + 3
	n=1		7n + 3

∞	(n	2	+ 9)4	n
е) ∑(−1)n+1	(n		+ 9)4
n=1	(n + 8)!
n=1

	∞			n	3	+	4n	2
б)	∑			n		+	4n
б)	∑				n9 + 36
	n=1				n9 + 36
	∞			n	n+5
г)	∑			n
г)	∑		(n + 8)!
	n=1		(n + 8)!
	n=1
е)
∞		7n − 4					3n+8
∑(−1)n+1		5n + 9
n=1		5n + 9

∞	5n	2	+ 2
б) ∑
	3 n9 + 3n2
n=1

∑∞ 5n + 9 n2

г) n=1 5n − 9

∞	4	n	(3n	+ 8)
е) ∑(−1)n+1
n=1		(n + 4)!

252

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2725 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.201979.36 Кб10планы семинаров Н.П.Шевченко.doc
#
01.11.20183.81 Mб146Подвижной состав. Исправленное.doc
#
12.11.2019176.64 Кб6пособие для поведния семинрских знятий.doc
#
15.02.201530.97 Mб31пособие проводнику.docx
#
15.02.201523.98 Кб22почтовобагажный вагон.docx
#
15.02.20153.83 Mб98практикум математика часть 2.pdf
#
15.02.20154.76 Mб121практикум по математике часть 3.pdf
#
15.02.2015328.84 Кб47Практич_МТТ_с_приложением_МТТ.pdf
#
15.02.2015439.81 Кб33Практическое занятие.doc
#
18.09.201934.46 Кб4Предпринимательство.docx
#
15.02.201530.21 Кб12прием док-в в общ-е (1).doc