Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский институт железнодорожного транспорта, филиал ИрГУПС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

практикум математика часть 2.pdf

Скачиваний:

107

Добавлен:

15.02.2015

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2714 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Рис.3.20

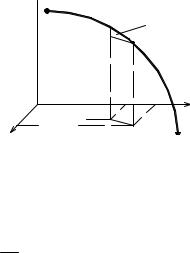
3.4. Криволинейные интегралы

Взависимости от величины (функции, поля), которая интегрируется по дуге (кривой) существует два рода криволинейных интегралов:

при интегрировании скалярной величины – интеграл I рода, при интегрировании векторной величины – интеграл II рода.

z A

xi x

3.4.1.Криволинейный интеграл I рода

3.4.1.1.Определение

f(x i, yi, zi)

Криволинейным интегралом I рода от скалярной функции f(x,y,z) по дуге AB называется предел интегральной суммы

	n	li = ∫ f (x, y, z)dl , где
lim ∑ f (xi , yi , zi )		li = ∫ f (x, y, z)dl , где
n→∞	i=1	AB
max	l→0

f(x,y,z) непрерывная скалярная функция в трехмерном пространстве на дуге AB(рис. 3.20), ∆li – длина i-ой элементарной дуги, на которые разбита вся дуга AB,

(i =1, n),

n – количество элементарных дуг,

		f(xi,yi,zi) – значение функции в точке (xi,yi,zi), принадлежащей
элементарной дуге ∆li.
		Если f(x,y,z) – линейная плотность распределения вещества на дуге AB
	кг	, то f(xi,yi,zi) ∆li – массаэлементарного куска дуги AB, интегральная сумма

	м

– приближенное значение, а ее предел – точное значение массы вещества в дуге AB (прута).

Физический смысл криволинейного интеграла I рода – это есть масса

вещества, заключенной в дуге AB (пруте, проводе и т.д.)

3.4.1.2. Вычисление криволинейного интеграла I рода

Вычисление сводится к расчету определенного интеграла.

Предварительно из рис. 3.20 следует:

li =

xi2

+ yi2 + zi2 . При переходе к

пределу интегральной суммы: dl =

dx 2

+ dy 2 + dz 2 .

Интегрирование определенного интеграла производится по одной

переменной. Поэтому переменные x, y, z, описывающие дугу AB в

трехмерном пространстве должны быть заданы параметрически.

= x(t)

Тогда

= y(t)

= z(t)

dl =

+ dy

+ dz

dt = (xt′) +(yt′)

+(zt′) dt.

t1 ≤ t ≤ t2

∫

f (x, y, z)dl = ∫2

f [x(t), y(t), z(t)]

(xt′)2 +(yt′)2 +(zt′)2 dt.

(3.1)

Если скалярная функция f(x,y) задана на дуге AB в двухмерном

пространстве, то существуют следующие формулы расчета криволинейного

интеграла I рода.

Для дуги AB, заданной параметрически:

x = x(t), y = y(t),t1 ≤ t ≤ t2 .

∫ f (x, y)dl = ∫2

f [x(t), y(t)]

(xt′)2

+ (yt′)2 dt .

(3.2)

Для

дуги

AB,

заданной гладкой

функцией

y = y(x), y(a) = A, y(b) = B (рис. 3.21).

(

)

(

)

dl =

+ dy

dx =

dx .

1 +

1 + (y′x )

b x

Рис.3.21

∫ f (x, y)dl = ∫b		f [x, y(x)] 1 + (y′x )2 dx .	(3.3)
AB	a

3.Для дуги AB, заданной гладкой функцией x = x( y), x(c) = B, x(d ) = A

(рис. 3.21).

	dl =			2
	dl =	dx2 + dy2 = dx		+1dy = 1+(x′y )2 dy .

			dy
	∫ f (x, y)dl = ∫c		f [x( y), y]		1 + (x′y )2 dy .		(3.4)
	AB	d
Замечание: для криволинейного интеграла I рода:						∫	= ∫ .
						AB	BA
4.	Для дуги	AB, заданной		в	полярной	системе координат:

r= r(ϕ),ϕ1 ≤ϕ ≤ϕ2 .

x = r cosϕ, y = r sinϕ, dx = (rϕ′ cosϕ − r sinϕ)dϕ, dy = (rϕ′ sinϕ + r cosϕ)dϕ, dl = dx2 + dy 2 =

= (rϕ′ cosϕ)2 − 2rrϕ′ cosϕ sinϕ + (r sinϕ)2 + (rϕ′ sinϕ)2 + 2rrϕ′ cosϕ sinϕ + (r cosϕ)2 dϕ = r 2 + (rϕ′)2 dϕ.

	ϕ	f [r cosϕ, r sinϕ] r 2 + (rϕ′)2 dϕ.
∫ f (x, y)dl = ∫2		f [r cosϕ, r sinϕ] r 2 + (rϕ′)2 dϕ.	(3.5)
AB	ϕ1

3.4.1.3.Некоторые приложения криволинейного интеграла I рода

1.Вычисление массы дуги (прута) AB с линейной плотностью вещества f(x,y,z).

m = ∫ f (x, y, z)dl

2.Вычисление длины дуги AB (если f(x,y,z) = 1).

L = ∫dl

3.Координаты центра масс xc, yc, zc дуги AB массой m.

	∫xf (x, y, z)dl		∫ yf (x, y, z)dl			∫zf (x, y, z)dl
xc =	AB	, yc =	AB		, zc =	AB
	m		m			m

4.	Моменты инерции Ix, Iy,			Iz, IO		дуги AB массой m относительно

осей Ox, Oy, Oz и начала координат.

I x = ∫(y 2 + z 2 )f (x, y, z)dl,I y = ∫(x2 + z 2 )f (x, y, z)dl, I z = ∫(x2 + y 2 )f (x, y, z)dl,

IO = ∫(x2 + y 2 + z 2 )f (x, y, z)dl.

При расчетах перечисленных величин в трехмерном пространстве следует пользоваться формулой (3.1), а в двухмерном пространстве формулами (3.2), (3.3), (3.4), (3.5).

3.4.1.4. Типовые примеры решения криволинейных интегралов I

рода.

	z
	2
	C
B	1

x 1

Рис.3. 22

Пример 1. Вычислить ∫(x2 y + 2z)dl , где AB –

		ABC
	дуга винтовой линии	x = cos t, y = sin t, z =	t	,0 ≤ t ≤ 2π;
	дуга винтовой линии	x = cos t, y = sin t, z =		,0 ≤ t ≤ 2π;
		6
	BC – отрезок прямой;	A(1;0;0), B(1;0;1), C(1;1;2).
y	Решение. Кривая интегрирования – ломаная
	ABC (рис.3. 22).

∫ = ∫ + ∫ .

			ABC AB		BC
•			x = cos t, y = sin t, z = t		6,0	≤ t ≤ 2π •
•

∫(x2 y + 2z)dl=	dl = (xt′)2 +(yt′)2 +(zt′)2 dt =								=
AB		=	(−sin t)2 +cos2 t +	1	dt	=	37	dt
		=	(−sin t)2 +cos2 t +		dt	=	6	dt
	•		36				6		•
									•

2π	2		t	37		37	2π	2		37	2π
= ∫ cos		t sin t + 2			dt = −		∫cos		t d cos t +		∫tdt =
			6	6		6				18
0							0				0

		= −		37	cos3 t			2π	+	37			t 2		2π		= −		37		(1	−1)+		37		4π 2			=		37			π 2 .
		= −							+								= −				(1	−1)+							=					π 2 .
				6		3		0		18	2				0				18					18			2			9
∫(x2 y + 2z)dl=•							• BC :		y − 0		=	z −1				, y = z −1, dy = dz, x =1, dx = 0, dl = dx2 + dy2 + dz 2 =
									y − 0			z −1
									1 − 0			2 −1
BC									1 − 0			2 −1
	•		2	2										2								3		2				2				3						7


= 2dz		• =	∫	(1 (z −1)+ 2z) 2dz = 2 ∫												(3z −1)dz =						2	z		− z			=		2			(4 −1)		−(2	−1)	=		2.
= 2dz		• =	∫	(1 (z −1)+ 2z) 2dz = 2 ∫												(3z −1)dz =						2	z		− z			=		2			(4 −1)		−(2	−1)	=		2.
			1											1								2						1				2						2
							∫ (x2 y + 2z)dl =										37	π	2 +	7		2 =	1		(2 37π 2 + 63 2 ).
							∫ (x2 y + 2z)dl =										9	π	2 +	2		2 =	18		(2 37π 2 + 63 2 ).
							ABC										9			2			18

Замечание. Здесь и далее знаком ∙│∙ выделены пояснения.

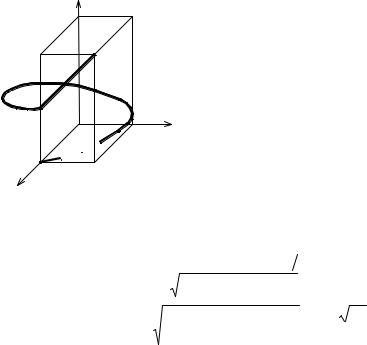
Пример 2. Найти массу дуги AB кривой γ, если ее линейная плотность меняется по закону ρ (M).

x = cost +t sin t

- эвольвента окружности, A(1;0), B(1;−2π), ρ(M ) = x2 + y 2 .

γ :

y = sin t −t cost

Решение. Нетрудно видеть, что при движении от A к B параметр t

меняется от 0 до 2π, т.е. 0 ≤ t ≤ 2π . Масса дуги определяется по формуле:

m = ∫ρ(M )dl = ∫

x2 + y2

dx2 + dy2 =•

x = cos t + t sin t; dx = (−sin t + sin t + t cos t)dt•

•

y = sin t − t cos t; dy = (cos t − cos t + t sin t)dt

•

2∫π (cost + t sin t)2

+ (sin t −t cost)2

t 2 cos2 t + t 2 sin 2 tdt =

2∫π

1 + t 2 tdt =

2∫π(t 2

+1)1 2 d(t 2

+1)=

(t 2 +1)3 2

2π

((2π )2 +1)3 −1

ед. массы.

2 0

3.4.1.5.Задания на контрольную работу

Задание 1. Вычислить.

∫x2 dl , AB – кривая y = ln x,1 ≤ x ≤ 2.

∫xdl , AB – кривая y = x2 , A(2;4), B(1;1).

∫

, AB – отрезок прямой,

A(0;−2), B(4;0).

+ y

∫γ

, γ – винтовая линия x = a cos t, y = a sin t; z = bt,0 ≤ t ≤ 2π.

x 2

+ y 2 + z 2

∫(x + y)dl , γ – правый лепесток лемнискаты r 2 = a2 cos 2ϕ.

∫

+ y 2 dl , γ – дуга кривой x = a(cost + t sin t), y = a(sin t −t cost),0 ≤ t ≤ 2π.

∫y2 dl , γ – первая арка циклоиды x = a(t −sin t), y = a(1 −cost).

∫xydl , γ – четверть эллипса

=1, x ≥ 0, y ≥ 0.

∫

, OA – отрезок прямой, O(0,0), A(1,2).

+ y

+ 4

10. ∫xyzdl , γ – винтовая линия x = a cos t, y = a sin t, z = bt,0 ≤ t ≤ 2π.

Задание 2. Найти массу дуги AB кривой γ, если ее линейная плотность

меняется по закону ρ(M).

= 3 cos t

, x ≥ 0, y ≥ 0, A(3;0), B(0;3), ρ(M )= xy.

γ :

= 3sin t

F (x, y, z)

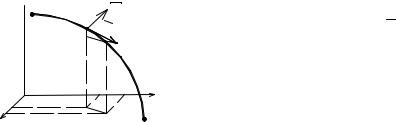
2.	γ : x = cos3 t , x ≥ 0, y	≥ 0, A(1;0), B(0;1), ρ(M )= x2 + y2 .
	y = sin3 t
3.	x = 2 sin t − sin 2t		, x ≥ 0,	A(0;1), B(0;−3), ρ(M )= x.
3.	γ :		, x ≥ 0,	A(0;1), B(0;−3), ρ(M )= x.
	y = 2 cos t − cos 2t

4.γ : x = t − sin t , A(0;0), B(2π;0), ρ(M )= y.y =1 − cos t

5.γ : x = cos t + t sin t , A(1;0), B π ;1 , ρ(M )= x.y = sin t − t cos t 2

6.γ : x = et (cost +sin t), A(1;1), B(−eπ ;−eπ ), ρ(M )= x2 + y2 .

y = et (cost −sin t)

7.	γ : x = (t 2 −2)sin t + 2t cost						, A(0;2), B(−2π;π 2 −2), ρ(M )= x2 + y2 .
	y = (2 −t 2 )cost + 2t sin t
8.	x	= 2(t − sin t)			, A(0;0), B(2π;4), ρ(M )= y2 .
8.	γ :	= 2(1 − cos t)			, A(0;0), B(2π;4), ρ(M )= y2 .
	y	= 2(1 − cos t)
9.	x	= 2 cos t	, x ≥		0, y ≥	0,	A(2;0), B(0;5), ρ(M )= xy.
9.	γ :		, x ≥		0, y ≥	0,	A(2;0), B(0;5), ρ(M )= xy.
	y = 5sin t
			3
10. γ : x = 2 cos			3	t , x ≥ 0, y		≥ 0, A(0;2), B(2;0), ρ(M )= xy.
10. γ : x = 2 cos				t , x ≥ 0, y		≥ 0, A(0;2), B(2;0), ρ(M )= xy.
	y = 2 sin3 t

3.4.2. Криволинейный интеграл II рода

3.4.2.1. Определение

zA F(xi, yi, zi)

zi	li
xix	yi	y
		y
		B

Рис. 3.23

непрерывная векторная

Криволинейным интегралом II рода от векторной функции по дуге AB

называется предел интегральной суммы

___

lim∑

(xi , yi , zi ) li = ∫

(x, y, z) dl

= ∫

, где

n→∞ i=1

l→0

(x, y, z) = Fx (x, y, z)i

+ Fy (x, y, z) j + Fz (x, y, z)k –

функция

(векторное

поле) в

трехмерном

пространстве на дуге AB (рис.3.23),

li = xii + yi j + zi k - вектор i-ой элементарной дуги, на которые разбита вся

____

дуга AB, (i = 1, n) , направлен он по касательной к элементарной дуге, xi , yi , zi - соответствующие координаты вектора li ,

n – количество элементарных дуг,

F (xi , yi , zi ) - значение векторной функции F в точке (xi , yi , zi ), принадлежащей i-ой элементарной дуге,

(xi , yi , zi )

li - скалярное произведение указанных векторов.

При

переходе от

интегральной суммы к ее пределу

li =

xi i

yi j + zi k преобразуется в dl = dxi + dyj + dzk и тогда криволинейный

интеграл II рода

∫

= ∫(Fx (x, y, z)i

+ Fy (x, y, z,)

+ Fz (x, y, z)k

) (dxi

+ dyj

+ dzk

)= ∫Fx dx + Fy dy + Fz dz.

По последнему виду этот интеграл еще называют интегралом по координатам, а иногда линейным (в силу линейности подынтегрального выражения).

Последний вид интеграла понимается как

∫Fx dx + Fy dy + Fz dz = ∫Fx dx + ∫Fy dy + ∫Fz dz.

Если

вектор

= dxi

+ dyj

+ dzk

представить

как произведение

единичного

вектора

n =

на

модуль

вектора

= dl , то

∫

= ∫

ndl = ∫ f (x, y, z)dl , где

скалярное

произведение векторов

n есть

скалярная функция f(x,y,z). Этим самым показывается связь криволинейных интегралов I и II родов.

Если Fr(x, y, z) – вектор силы на дуге AB, то скалярное произведение векторов F (xi , yi , zi ) li есть элементарная работа Ai силы F на i-ой

элементарной дуге, интегральная сумма – приближенное значение, а ее предел – точное значение работы A, которую затрачивает сила F по дуге AB.

Механический смысл криволинейного интеграла II рода – это есть работа, затрачиваемая силой F по дуге AB.

Если векторная функция есть напряженность электростатического поля E (x, y, z), то известные из электростатики соотношения физических величин

приводят к тому, что скалярное произведение

, El =

E =

векторов

(xi , yi , zi )

- элементарное электрическое напряжение на концах

i-ой элементарной дуги, интегральная сумма – приближенное значение, а ее предел – точное значение электрического напряжения UAB на концах дуги AB.

Электротехнический смысл криволинейного интеграла II рода – это есть электрическое напряжение между точками AB в электростатическом поле с напряженностью E.

U AB = ∫E dl.

3.4.2.2. Вычисление криволинейного интеграла II рода

Вычисление сводится к расчету определенного интеграла.

Если дуга AB задана в трехмерном пространстве, а интегрировать нужно по одной переменной (однократно), то задавать уравнение дуги AB нужно параметрически.

x = x(t)	dx = xt′dt
	dy = yt′dt t1 ≤ t ≤ t2 .
y = y(t)	dy = yt′dt t1 ≤ t ≤ t2 .
	dz = zt′dt
z = z(t)	dz = zt′dt

Тогда

∫F dl = ∫Fx (x, y, z)dx + Fy (x, y, z)dy + Fz (x, y, z)dz =

AB AB

= t∫2	(Fx (x(t), y(t), z(t))xt′ + Fy (x(t), y(t), z(t))yt′ + Fz (x(t), y(t), z(t))zt′)dt	(3.6)
t1

Если векторное поле F (x, y) задано на дуге AB в двухмерном пространстве, то вычисление криволинейного интеграла II рода можно производить по любой из следующих формул.

1.Для дуги AB, заданной параметрически:

x = x(t), y = y(t),t1 ≤ t ≤ t2

∫			= t∫2	(Fx (x(t), y(t))xt′ + Fy (x(t), y(t))yt′)dt.	(3.7)
		dl
	F
AB			t1

2.Для дуги AB, заданной гладкой функцией y = y(x), y(a) = A, y(b) = B

(рис. 3.21.)

∫			= ∫b (Fx (x, y(x))+ Fy (x, y(x))y′x )dx	(3.8)
		dl
	F
AB			a

3.Для дуги AB, заданной гладкой функцией x = x( y), x(c) = B, x(d ) = A

(рис. 3.21.)

∫			= ∫c (Fx (x( y), y)x′y + Fy (x( y), y))dy	(3.9)
		dl
	F
AB			d

Если кривая интегрирования замкнута, т.е. A и B совпадают, то криволинейный интеграл II рода называется циркуляцией вектора F по контуру l:

Ц = ∫ F dl.

При этом, очень важно указывать стрелочкой в контуре направление

интегрирования, т.к. для криволинейного интеграла II рода ∫	= − ∫ .
AB	BA

B(x, y, z) z

C(x, y0, z0)

z0 x 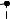D(x, y, z0)

y0 y y

A(x0, y0, z0) x0

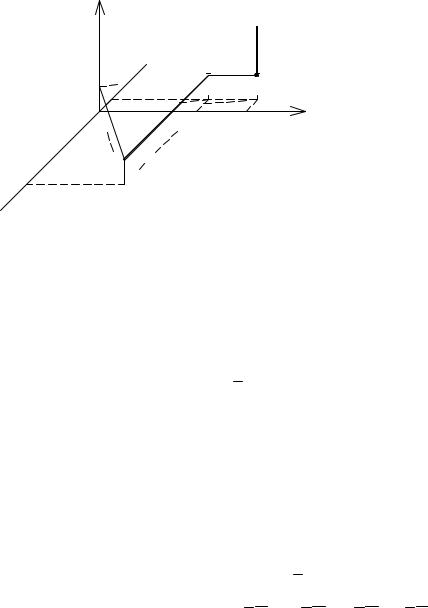
Рис. 3.24

В практике вычислений криволинейного интеграла II рода особое место занимают интегралы инвариантные (независимые) от кривой интегрирования. Условия инвариантности выводят из формул Грина и Стокса и достаточно широко отображены в литературе.

Для таких интегралов форма кривой безразлична, поэтому выбирают такую форму, для которой расчет интеграла был бы самым простым.

Классическим примером такого расчета являемся формула определения потенциала векторного поля.

Если векторное поле F потенциально (условия потенциальности см. стр.166), то оно инвариантно к кривой интегрирования, и дугу AB заменяют на самую простую ломаную AB (рис.3.24), состоящую из трех отрезков прямых параллельных соответствующей одной из координатных осей. Тогда уравнения каждого отрезка представляют собой одну из переменных при постоянстве двух других переменных.

Потенциал φ векторного поля F равен:

ϕ = ∫ F dl = ∫ F dl + ∫F dl + ∫F dl.

•

y = y0

, dy = 0

•

∫ Fdl = ∫Fx (x, y, z)dx + Fy (x, y, z)dy + Fz (x, y, z)dz=

∫Fx (x, y0 , z0 )dx,

z = z0

, dz = 0

•

Fx (x, y, z)dx + Fy (x, y, z)dy + Fz (x, y, z)dz=

•

z = z0 , dz = 0

•

Fy (x, y, z0 )dy,

∫

F dl =

x −const, dx = 0

•

(x, y, z)dx + F

(x, y, z)dy + F (x, y, z)dz=

• x −const, dx = 0•

= z

F (x, y, z)dz,

∫

y −const, dy = 0

∫

•

ϕ = ∫

= ∫Fx (x, y0 , z0 )dx +∫Fy

(x, y, z0 )dy + ∫Fz (x, y, z)dz.

(3.10)

3.4.2.3.Некоторые приложения криволинейного интеграла II рода.

1.Вычисление работы A силы F по кривой AB.

A = ∫F dl .

2. Вычисление электрического напряжения U в электростатическом поле с напряженностью E .

U = ∫E dl .

3. Площадь фигуры на плоскости, например, на плоскости z = 0, ограниченной замкнутой линией γ.

S= 1 ∫xdy − ydx. 2 γ

3.4.2.4.Типовые примеры решения криволинейных интегралов II

рода.

z	Пример 1. Вычислить
	C	∫(x2 + 2 yz)dx + (y 2 + 2xz)dy + (z 2 + 2xy)dz,
1		∫(x2 + 2 yz)dx + (y 2 + 2xz)dy + (z 2 + 2xy)dz,
		ABC
B	y AB	–	отрезок		прямой,	BC	–	дуга
1	y AB	–	отрезок		прямой,	BC	–	дуга
1	y = x2 , z =1, A(1;0;0), B(1;1;1),C(−1;1;1).
A
x		Начертить линию интегрирования.
Рис. 3.25		Решение. Линия интегрирования – рис. 3.25.
		∫	= ∫	+ ∫ .
		ABC	AB	BC

∫(x2 + 2 yz)dx + (y 2 + 2xz)dy + (z 2 + 2xy)dz =

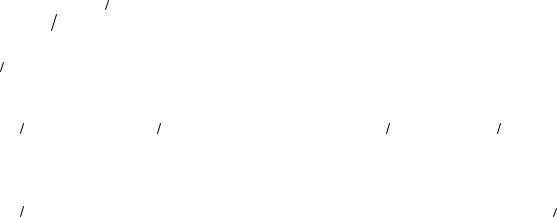
• AB :

y − 0

z − 0

, y = z, x =1, dy = dz, dx = 0•

1 − 0

•

1 − 0

•

= ∫(y

2 y)dy + (y

+ 2 y)dy = 2∫(y

+ 2 y)dy

+ y

∫(x2

+ 2 yz)dx + (y 2 + 2xz)dy + (z 2 + 2xy)dz=•

• BC : y = x2 , z =1, dy = 2xdx, dz = 0•

• =

−1

= ∫(x

)dx +(x

+ 2x)2xdx = ∫(2x

+7x

)dx =

−1)+

(−1

−1)

= −

∫ =

−

= −2.

ABC

Пример 2. Вычислить работу

силового

поля

при

перемещении

материальной точки вдоль дуги кривой γ от точки A до точки B.

= 2 cos t, y = 2 sin t,

F = (y 2 − z)i + (z 2

− x)j + (x2 − y)k ,

γ :

z = sin t,

A(2;0;0), B(0;2;1).

Решение. Нетрудно видеть, что при перемещении материальной точки от A к B параметр t кривой γ меняется от 0 до π2 .

A = ∫

= ∫(y 2

− z)dx + (z 2

− x)dy + (x2 − y)dz=•

• dx = −2sin tdt, dy = 2 cos tdt, dz = cos tdt,

0 ≤ t ≤ π 2•

•

= π∫2((4sin 2 t −sin t)(− 2sin t)+ (sin 2 t − 2 cos t) 2 cost + (4 cos2 t − 2sin t) cos t)dt =

π∫2(−8sin3 t + 2sin 2 t + 2sin 2 t cost − 4 cos2 t + 4 cos3 t − 2sin t cost)dt =

π 2

1 − cos 2t

1 + cos 2t

π 2

= 8 ∫ (1 − cos

t)d cost +

∫

− 4

+ 2 ∫ sin

td sin t + 4 ∫(1 −sin

t)d sin t −

π 2

cos

sin

π 2

− 2 ∫ sin td sin t =

8cost −8

−t −

sin 2t + 2

+ 4sin t

− 4

− 2

= −3 −

π ед. работы.

Пример

Найти

циркуляцию

вектора

вдоль контура γ ,

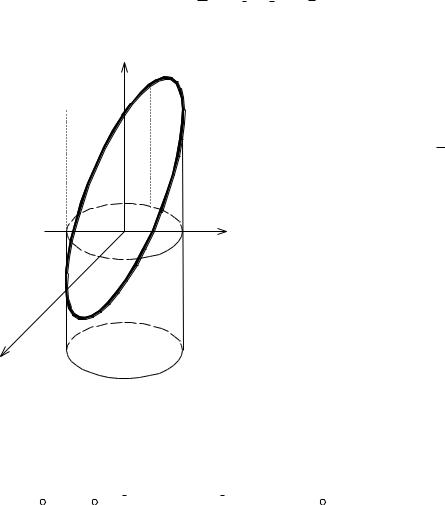
образованного пересечением двух поверхностей. Построить чертеж.

		F = 3yi − zj + 2xk ,γ : x2 + y2 = 9,
		2x − y + z = 2.
z		Решение. При пересечении данных
		поверхностей образуется контур – наклонный
		в пространстве эллипс (рис. 3.26). Чтобы найти
		циркуляцию вектора F вдоль этого эллипса,
		необходимо	вывести	аналитические
		выражения его в параметрической форме.
-3	3	y
		x = r cos t, y = r sin t, x2 + y 2 = 9, r 2 cos2 t + r 2 sin 2 t = 9,

r 2 = 9, r = 3.

2x − y + z = 2,2r cos t − r sin t + z = 2,6 cos t − 2 sin t + z = 2.

x = 3cos t,

dx = 3(−sin t)dt,

y = 3sin t,

dy = 3cos tdt,

− 6 cos t + 2sin t,

dz = (6sin t + 2 cos t)dt.

z = 2

0 ≤ t ≤ 2π,

Рис.3.26

Циркуляция вектора равна:

Ц = ∫

= ∫(3yi

)(dxi

+ dyj

+ dzk

)= ∫3ydx − zdy + 2xdz =

+ 2xk

− zj

2∫π(3 3sin t 3(−sin t)−(2 −6 cost + 2sin t)3cost + 2 3cost(6sin t + 2 cost))dt =

2∫π(− 27sin 2 t −6cost +18cos2 t −6sin t cost +36cost sin t +12cos2 t)dt =

2∫π(− 27sin 2 t +30cos2 t +30sin t cost −6cost)dt =

2π

(− 27)

1−cos 2t

1+ cos 2t

= ∫

+30

+15sin 2t

−6cost dt =

2π

= ∫

−

cos 2t +

cos 2t

+15sin 2t −6cost dt =

2π

= ∫

cos 2t +15sin 2t

−6cost dt =

t +

sin 2t

−

cos 2t −6sin t

= 3π.

3.4.2.5. Задания на контрольную работу

Задание 1. Вычислить интеграл, начертить линию интегрирования.

1.	∫(2 y + x)dx + 4xyzdy + xdz, AB – дуга y = x2 −3x + 2, z = 2,
ABC
		BC – отрезок прямой,					A(1;0;2), B(0;2;2);C(0;0;0).
2.	∫(y − x + 2z)dx + 2xyzdy + y 2 dz, ABС – ломаная, A(2;1;2), B(−1;1;0);C(−1;2;1).
ABC
3.	∫2xyzdx + (2z + x + y)dy + (z + x)dz, AB – дуга z = 3 y, x = −1;
ABC
		BC – отрезок прямой,					A(−1;1;1), B(−1;−1;−1);C(0;−1;1).
4.	∫(x − 2 y + z)dx + (y −3x − 2)dy + yzdz, AB – дуга z = x −1, y =1;
ABC
		BC – отрезок прямой,					A(2;1;1), B(1;1;0);C(1;2;2).
5.	∫(2 y −3x − z)dx + (4xy + 2z)dy + x2 zdz, AB – дуга y = 3x2 − x +1, z = 2;
ABC
		BC – отрезок прямой,					A(1;3;2), B(3;25;2);C(3;0;0).
6.	∫(2x − y − z)dx − 2xy2 zdy −5x2 dz, AB – отрезок прямой,
ABC
		BC – дуга y = z 2 − 4z + 4, x =1, A(2;−3;1), B(1;1;1);C(1;4;4).
7.	∫sin ydx + x2 zdy − y 2 xdz, AB – дуга y = 2 x, z = 0;
	ABC
		BC – отрезок прямой,					A(0;0;0), B(4;4;0);C(4;0;4).
8.	∫	zdy	−	zdx		+ xy2 dz, AB – дуга y = 3 x, z = 4;
8.	∫		−			+ xy2 dz, AB – дуга y = 3 x, z = 4;
ABC		x			y
		BC – отрезок прямой,					A(1;1;4), B(8;2;4);C(8;0;0).
9.	∫(x2 − y 2				+ z 2 )dx + (x2 + y 2 − z 2 )dy + xyzdz, AB – отрезок прямой,
ABC
		BC – дуга y = x3 , z = 2,					A(0;1;0), B(1;1;2); C(−1;−1;2).
10.	∫(2 y −3x + z 2 )dx − (x cos y + 2z)dy − z 2 dz, AB – отрезок прямой,
	ABC

BC – дуга x2 + z2 =1, y = 0 , A(0;2;1), B(0;0;−1);C(1;0;0).

Задание 2. Вычислить работу силового поля F при перемещении материальной точки вдоль дуги кривой γ от точки A до точки B.

,γ : x = cos t, y = sin t, z = cos t; A(1;0;1), B(−1;0;−1).

= 2 yi

+ xzj

+ yk

= xyi

+ z 2

,γ : x = cos t, y = sin t, z = 4 − cos t −sin t; A(1;0;3), B(−1;0;5).

+ xk

,γ : x = 5cos t, y = 5sin t, z = 4; A(5;0;4), B(−5;0;4).

= zi

− xzj

+ y 2 k

= xzi

, γ : x = 2 cos t, y = 2 sin t, z =1 − 2 cos t − 2 sin t; A(2;0;−1), B(0;2;−1).

+ xj

+ z 2 k

= y 2i

+ xyk

,γ : x = 2 cos t, y = 3sin t, z = 4 cos t −3sin t − 2; A(2;0;2), B(0;3;−5).

+ zj

+ 2z 2

+ yxk

,γ : x = 3cos t, y = 4sin t, z = 6 cos t − 4sin t +1; A(3;0;7), B(0;4;−3).

= xi

= y2i

, γ : x = 4 cos t, y = 3sin t, z = cos t − 3sin t − 3; A(4;0;−2), B(0;3;−6).

+ xzj

+ xk

= zxi

+ z 2

,γ : x = 2 cos t, y = sin t, z = 4 cos t −sin t −1; A(2;0;3), B(0;1;−2).

+ yk

9.F = z 2i + xj + xyk ,γ : x = 3cos t, y = 3sin t, z = 4; A(3;0;4), B(0;3;4).

10.F = yxi + x2 j + zk , γ : x = cos t, y = sin t, z = 4 sin t − 3 cos t; A(1;0;−3), B(0;1;4).

Задание 3. Найти циркуляцию вектора

вдоль контура γ ,

образованного пересечением двух поверхностей. Построить чертеж.

x2 + z2 = 4,

= 2zi

+ 4 yj − xk ,

γ :

x − y + 2z = 2.

= yzi

+ z2 k

z = 6(x2 + y2 )+ 2,

− 2xj

γ :

z = 8.

− 4 y2 k

x 2

+ y 2 + z 2 = 9,

= −zi

+ 2xj

γ :

+ y 2 = 4, z ≥ 0.

x 2

= x 2 i

+ y2

=16,

+ 2 yk

− 3zj

γ :

z = 2.

+ y2

= 4z2 ,

− zk ,

= 4yi

+ 2xzj

γ :

z =

= (3 − xy)i

− xk

y2 + z2 = 9,

+ 2zj

γ :

y −2x −4z = 4.

y = 4(x2 + z2 )−2,

= 5zi

+ xyj − xzk ,

γ :

y = 2.

= x2i

+ y2 k

+ y2 + z2 = 4,

− zj

γ :

y2 + z2 , x > 0.

= yzi

+ z2 = 9,

− xyk ,

+ 2xzj

γ :

y = 3.

10.

= 2z 2i

+ z2 = 9 y2 ,

− xyj

+ 4zk ,

γ :

y =1.

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2714 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.11.20183.81 Mб187Подвижной состав. Исправленное.doc
#
30.12.201984.44 Mб1Пособие 80Р.doc
#
12.11.2019176.64 Кб14пособие для поведния семинрских знятий.doc
#
15.02.201530.97 Mб33пособие проводнику.docx
#
15.02.201523.98 Кб26почтовобагажный вагон.docx
#
15.02.20153.83 Mб107практикум математика часть 2.pdf
#
15.02.20154.76 Mб123практикум по математике часть 3.pdf
#
15.02.2015328.84 Кб49Практич_МТТ_с_приложением_МТТ.pdf
#
15.02.2015439.81 Кб35Практическое занятие.doc
#
18.09.201934.46 Кб6Предпринимательство.docx
#
15.02.201530.21 Кб14прием док-в в общ-е (1).doc