
- •Красноярск 2006
- •Предисловие
- •1. Неопределенный и определенный интегралы
- •1.1. Определение неопределенного интеграла. Методы интегрирования
- •Решение:
- •Применяя указанные формулы, получим
- •1.2.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
- •Понятие определенного интеграла
- •Свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Теорема. Если функция f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке, то имеет место следующая формула:
- •Метод замены переменной в определенных интегралах
- •Метод интегрирования по частям в определенных интегралах
- •Вычисление площадей плоских фигур
- •Параметрические функции
- •Вычисление длины дуги плоской кривой
- •Вычисление площади поверхности вращения
- •Объем тела вращения
- •1.3 Несобственные интегралы
- •2.3 Задания на контрольную работу
- •3.1.Общая методология интегралов
- •3.2. Двойной интеграл
- •Правила вычисления двойного интеграла в полярной системе координат
- •3.3. Тройной интеграл
- •3. 4. Криволинейные интегралы
- •3.5. Поверхностные интегралы
- •7. Элементы теории поля
- •Понятие функции комплексного переменного
- •Предел и непрерывность функции комплексного переменного
- •Производная ФКП. Условия Коши-Римана
- •Интегрирование ФКП
- •Ряд Лорана
- •Особые точки
- •Вычеты
- •Преобразование Лапласа
- •4.2.Решение типовых примеров и задач
- •4.3.Задания на контрольную работу
- •5.1.1.Классификация линейных дифференциальных уравнений в частных производных второго порядка
- •5.1.2.Начальные и краевые условия
- •5.1.3.Уравнение колебаний струны
- •5.1.4.Уравнение теплопроводности
- •5.1.5.Уравнение Лапласа
- •5.2. Решение типовых примеров и задач
- •5.3. Задания на контрольную работу
- •10. Ряды
- •Задание 2. Найти область сходимости рядов:
- •Практикум по математике
- •4.1.Краткие сведения из теории
- •Комплексные числа
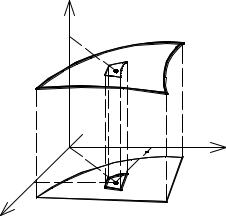
3.5.Поверхностные интегралы
Взависимости от величины (функции, поля), которая интегрируется по ограниченному куску гладкой кривой поверхности существуют два рода поверхностных интегралов.
При интегрировании скалярной величины (поля) – поверхностный интеграл I рода.
При интегрировании векторной величины (поля) – поверхностный интеграл II рода.
3.5.1.Поверхностный интеграл I рода
3.5.1.1.Определение
|
z |
|
Поверхностным интегралом I |
рода |
|
|
zi |
|
от скалярной функции ѓ(x,y,z) по |
||
|
σ |
Si |
ограниченному куску гладкой (кусочно- |
||
|
|
|
гладкой) поверхности σ называется |
||
|
|
yi |
предел интегральной суммы |
|
|
|
|
y |
n |
|
|
xi |
σxy |
xi yi |
n→∞lim ∑ f (xi , yi , zi ) |
Si = ∫∫ f (x, y, z)dS, |
где |
x |
|
max Si →0 i=1 |
σ |
|
|
|
|
ѓ(x,y,z) – ограниченная непрерывная |
|||
|
|
|
|||
|
|
|
скалярная функция (поле), |
|
|
|
|
Рис. 3.27 |
определённая на ограниченном куске |
||
гладкой поверхности σ (рис.3.27), |
Si – площадь i-ой элементарной площадки, |
||||
на которые разбит весь кусок поверхности σ, (i=1,n), n – количество элементарных площадок,
ѓ(xi,yi,zi) – значение функции в точке (xi,yi,zi) принадлежащей элементарной площадке Si.
100
Если ѓ(x,y,z) – поверхностная плотность распределения вещества [кг/м3], то ѓ(xi,yi,zi) Si - масса элементарного кусочка поверхности σ, интегральная сумма – приближённое значение, а её предел – точное значение массы всего куска поверхности σ.
Физический смысл поверхностного интеграла I рода – это есть масса куска кривой поверхности σ.
С помощью этого интеграла можно посчитать массу пустой цистерны, обшивки ракеты, корпуса подводной лодки и т. п.
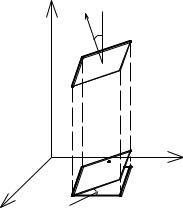
3.5.1.2. Вычисление поверхностного интеграла I рода.
|
z |
ni |
γ |
Расчёт |
сводится |
к вычислению |
|
|
двойного |
интеграла. |
Общеизвестно, |
||
|
|
|
Si |
|||
|
|
|
что двойной интеграл вычисляется по |
|||
|
|
|
|
|||
|
|
|
|
плоской области D. Значит нужен |
||
|
|
|
|
переход от куска кривой поверхности |
||
|
|
|
y |
σ к плоской области D. Этот переход |
||
|
|
|
xi |
осуществляется через проекцию σ на |
||
x |
|
γ |
yi |
|||
|
любую из координатных плоскостей, |
|||||
|
|
|
|
|||
|
Рис. 3.28 |
лишь бы выполнялось условие |
||||
однозначности проектирования.Чтобы осуществить этот выбор нужно обязательно иметь чертёж задачи.
Пусть поверхность σ однозначно проектируется на плоскость Z = 0 и эта проекция есть область σxy (рис. 3.27). Тогда каждая из элементарных площадок Si будет иметь проекцию на плоскость Z = 0 в виде xi yi (рис. 3.28).
101
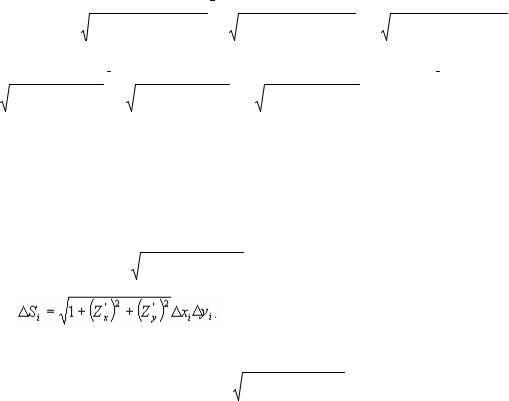
Элементарная площадка Si – кусочек плоскости изменяющей свою ориентацию от точки к точке по поверхности σ, площадка xi yi – тоже кусочек плоскости, но с постоянной ориентацией, так как лежит на самой плоскости Z = 0. Их площади связаны соотношением:
xi yi = cosγ, где γ - угол между их плоскостями.
Si
Но угол γ, это угол между единичным нормальным вектором ni
площадки Si и осью Oz (рис. 3.28), являющейся нормальным вектором площадки xi yi .
Напомним, если гладкая двухсторонняя поверхность σ задана уравнением Z = Z(x,y) или φ(x,y,z) = Z-Z(x,y) = 0, то единичный нормальный вектор к такой поверхности определяется как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
gradϕ |
|
|
|
|
ϕx' |
|
|
|
|
|
|
|
|
ϕy |
|
|
|
|
|
|
|
|
|
ϕz' |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n = ± |
|
|
|
|
= ± |
|
|
|
|
|
|
i + |
|
|
|
|
|
|
|
|
|
|
|
j + |
|
|
|
|
k |
= |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
gradϕ |
|
|
(ϕx' )2 +(ϕy' )2 +(ϕz' )2 |
|
|
|
(ϕx' )2 +(ϕy' )2 +(ϕz' )2 |
|
|
|
|
|
(ϕx' )2 +(ϕy' )2 +(ϕz' |
)2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
−Zx' |
|
|
−Zy |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=±(cosαi +cosβ j |
+cosγk), |
|||||||||||||||||||||
= ± |
|
|
|
|
|
|
|
i + |
|
|
|
|
|
|
|
j + |
|
|
|
|
|
|
|
k |
||||||||||||||||
|
1+(Z ' |
|
)2 +(Z ' |
)2 |
1+(Z ' |
)2 |
+(Z ' |
)2 |
|
1+(Z |
|
)2 |
+(Z ' |
)2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x |
|
|
y |
|
|
x |
|
|
y |
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где cosα ,cos β ,cosγ |
- направляющие косинусы. |
|
(3.11) |
|||
Поверхностный интеграл I рода, определяющий массу поверхности, не |
||||||
зависит от направления вектора |
|
, поэтому знаки ± опускаем. |
|
|||
n |
|
|||||
Откуда cosγ = |
1 |
|
|
и xi yi = cosγ Si , |
xi yi |
|
|
Si = cosγ |
, |
||||
1+ (Z x' )2 +(Z y' )2 |
||||||
При переходе от интегральной суммы к её пределу имеем:
dxdy = cosγ dS, |
dS = dxdy |
, dS = 1+(Zx' |
)2 |
+(Z y' )2 dxdy . |
(3.12) |
|
cosγ |
|
|
|
|
Таким образом, если функция ѓ(x,y,z) задана на поверхности σ, которая описывается уравнением Z = Z(x,y), и поверхность σ однозначно
102
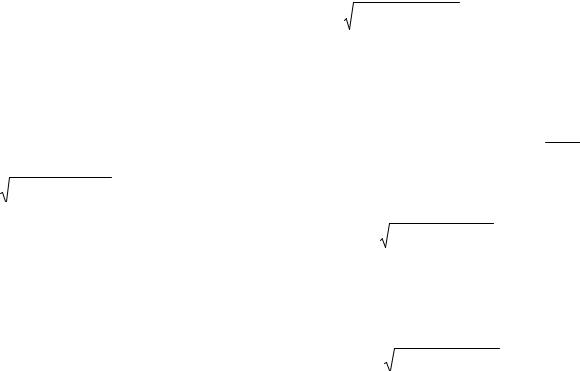
проектируется на плоскость Z = 0, то поверхностный интеграл I рода вычисляется:
∫∫ f (x, y, z)dS = ∫∫ f (x, y, z(x, y)) |
dxdy |
= ∫∫ f (x, y, z(x, y)) 1 + (Z x' )2 + (Z y' )2 dxdy. |
(3.13) |
||||
cosγ |
|||||||
σ |
σ |
|
σ |
xy |
|
||
|
|
xy |
|
|
|||
Если поверхность σ однозначно проектируется на другие координатные плоскости, например, на X = 0, то уравнение поверхности σ задаётся в виде
X=X(y,z) и те же рассуждения приводят к формулам: dydz = cosαdS, dS = cosdydzα ,
dS = 1 + (x'y )2 |
+ (xz' )2 dydz , |
|
|
|
||
∫∫ f (x, y, z)dS = ∫∫ f (x(y, z), y, z) |
dydz |
=∫∫ f (x(y, z), y, z) 1+ (x'y )2 + (xz' )2 dydz . (3.14) |
||||
cosα |
||||||
σ |
σ |
yz |
σ |
yz |
||
|
|
|
|
|||
Если расчёт привязать к плоскости Y = 0, то уравнение σ есть Y=Y(x,z)
∫∫ f (x, y, z)dS = ∫∫ f (x, y(x, z), z) |
dxdz |
=∫∫ f (x, y(x, z), z) 1+ ( yx' )2 + ( yz' )2 dxdz (3.15) |
||||
cos β |
||||||
σ |
σ |
xz |
σ |
xz |
||
|
|
|
|
|||
Если проекции σ на координатные плоскости представляют собой фигуры, ограниченные окружностью или эллипсом, то расчёт поверхностного интеграла I рода (формулы (3.13),(3.14),(3.15)) удобнее проводить в полярной системе координат (см. расчёт двойного интеграла в полярной системе координат).
3.5.1.3.Некоторые приложения поверхностного интеграла I рода
1.Вычисление массы материальной поверхности с поверхностной плотностью распределения массы ѓ(x,y,z).
m = ∫∫ f (x, y, z)dS .
σ
2. Вычисление площади поверхности σ (если ѓ(x,y,z) = 1).
S = ∫∫dS .
σ
103
3. Вычисление координат центра масс Xc, Yc, Zc материальной
поверхности σ: xc = |
myz |
= |
∫∫xf (x, y, z)dS |
, yc = |
m |
xz |
= |
∫∫yf (x, y, z)dS |
, |
|||||||
σ |
σ |
|
||||||||||||||
m |
m |
|
|
|
m |
|||||||||||
|
|
|
|
|
|
|
|
m |
|
|||||||
zc = |
m |
xy |
|
∫∫zf (x, y, z)dS |
|
|
|
|
|
|
|
|
|
|||
= |
σ |
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|||
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||
где myz, mxz, mxy – статические моменты материальной поверхности σ относительно координатных плоскостей.
4. Вычисление моментов инерции Ix, Iy, Iz, Io относительно осей Оx,Оy,Оz и начала координат материальной поверхности σ.
I x = ∫∫(y2 + z2 )f (x, y, z)dS, I y = ∫∫(x2 + z2 )f (x, y, z)dS, I z = ∫∫(x2 + y2 )f (x, y, z)dS,
σ σ σ
I0 = ∫∫(x2 + y2 + z2 )f (x, y, z)dS .
σ
При расчётах перечисленных величин следует пользоваться формулами
(3.13, 3.14, 3.15).
3.5.1.4. Типовой пример решения поверхностных интегралов I рода
Пример. Вычислить массу, координаты центра масс и моменты инерции относительно координатных осей и начала координат материальной оболочки, которая представляет собой полую тонкостенную конструкцию, выполненную из композитного материала с поверхностной плотностью γ (x, y, z) [кг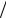 м2 ]. Оболочка имеет вид тела, ограниченного поверхностями S1, S2.
м2 ]. Оболочка имеет вид тела, ограниченного поверхностями S1, S2.
γ (x, y, z)= x2 , S1 : z = 2 − 12 (x2 + y2 ), S2 : z = 0.
Решение. Оболочка имеет вид тела – рис. 3.29, где S1 – “крыша”, S2 – основание.
104

|
z |
|
Масса оболочки |
|
|
|
||
|
|
m = ∫∫γ (x, y, z)dS |
= ∫∫x2 dS1 +∫∫x2 dS2 , |
|
|
|||
|
|
S1 |
|
|
||||
|
2 |
s |
S1 |
|
S2 |
|
|
|
|
|
|
|
|
||||
|
|
|
1 (x2 |
+ y2 ), |
|
|
||
|
|
|
S1 : z = 2 − |
|
|
|||
-2 |
S2 |
2 |
y |
2 |
|
|
|
|
(Z ' )2 |
+(Z ' |
)2 dxdy = |
|
|
||||
|
|
|
dS = 1+ |
1+ x2 |
+ y2 dxdy. |
|||
|
x |
|
1 |
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.29 |
S2 : z = 0 , dS2 = 1+(Zx' )2 +(Z y' )2 dxdy = dxdy. |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
1+ r 2 = t 2 ,t = 1+ r 2 , r = 0,t =1, |
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
∫r |
3 |
|
1+ r |
2 |
dr |
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
• r |
2 |
= t |
2 |
−1,2/rdr = 2/tdt, r |
= 2,t = |
|
|
5 • |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= ∫5(t 2 −1)ttdt = ∫5(t 4 −t 2 )dt = (t 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
− t3 ) |
5 |
= 1 |
(25 |
|
5 −1) − |
1 (5 |
5 −1) = |
10 |
|
5 + |
|
2 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
15 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
5 |
|
3 |
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
2π |
|
|
|
2 |
|
|
|
|
2 |
|
|
3 |
|
2 |
|
|
10 |
|
|
|
2 |
|
2π |
|
|
|
2 |
|
|
|
|
10 |
|
|
2 |
|
2π1 |
+ cos 2ϕ |
|
|
|
|
|
|
|||||||||||||||||||||
∫∫x |
|
dS1 |
= |
|
∫cos |
|
|
ϕdϕ∫r |
|
1+ r |
|
|
dr = |
|
|
|
|
5 + |
|
|
|
|
∫cos |
|
ϕdϕ |
= |
|
5 + |
|
|
|
∫ |
|
|
|
|
dϕ = |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
15 |
|
3 |
15 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
10 |
5 + |
|
|
|
2 |
|
|
|
1 |
ϕ + |
1 |
|
|
|
|
2π |
= |
10 |
5 + |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
3 |
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
0 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∫∫ |
x2 dS2 |
= |
∫∫ |
x2 dxdy=• |
|
x = r cosϕ, r = 2, |
|
|
|
|
|
|
|
|
• |
= |
2πcos2 |
ϕdϕ |
2 r3dr =2π |
1+ cos 2ϕ |
dϕ |
r 4 |
|
|
2 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
• dxdy = rdrdϕ,0 ≤ϕ ≤ 2π• |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
∫ |
|
|
|
∫ |
2 |
|
|
4 |
|
|
0 |
|
||||||||||||||||||||||||||||||||
S2 |
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
|
|
1 |
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
= 4π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
ϕ |
|
|
|
|
|
sin 2ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m = |
|
|
|
|
5 + |
|
|
|
|
π |
+ 4π = |
|
|
5 + |
|
|
|
π ≈ 36,401Ед.массы, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
3 |
|
15 |
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
координаты центра масс xc, yc, zc.
105

|
|
|
|
|
|
∫∫xγ (x, y, z)dS |
|
|
|
|
|
|
|
∫∫x3dS |
|
|
|
|
∫∫x3dS1 + ∫∫x3dS2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x |
= |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
S |
|
|
|
|
|
|
|
|
= |
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
c |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫∫x3dS1 =∫∫x3 |
|
|
|
|
1 + x2 + y2 dxdy =• |
|
|
|
x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
• |
|
= ∫∫r3 cos3 ϕ 1 + r 2 rdrdϕ = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S1 |
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
y = r sinϕ, dxdy = rdrdϕ |
|
|
|
• |
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2π |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
∫cos3 ϕdϕ∫r 4 |
|
1+ r 2 dr= |
|
|
|
∫r 4 |
|
1+ r 2 dr = A |
|
|
|
= A ∫(1−sin2 ϕ)d sinϕ = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
sin |
3 |
ϕ |
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
A sinϕ − |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
r |
5 |
|
2 |
|
|
|
|
32 |
|
sin |
3 |
ϕ |
|
|
|
|
2π |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
∫∫x |
3 |
dS2 = ∫∫x |
3 |
dxdy = ∫cos |
3 |
ϕdϕ∫r |
4 |
dr = ∫(1−sin |
2 |
ϕ)d sinϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
sinϕ − |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
5 |
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S2 |
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
∫∫yγ (x, y, z)dS |
|
|
|
|
|
|
∫∫yx2 dS |
|
|
|
|
|
|
∫∫yx2 dS1 + ∫∫yx2 dS2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
yc = |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
S |
|
|
|
|
|
|
|
|
= |
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫∫yx2 dS1 =∫∫yx2 |
|
1+ x2 + y2 dxdy =• |
|
|
x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
|
|
|
• |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S1 |
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
y = r sinϕ, dxdy = rdrdϕ |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
• |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= ∫∫r sinϕr 2 cos2 ϕ |
|
1+ r 2 rdrdϕ = ∫sinϕ cos2 ϕdϕ∫r 4 |
1+ r 2 dr= |
|
|
|
|
|
∫r 4 1+ r 2 dr = A |
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• 0 |
|
|
|
|
|
• |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= A2∫πcos2 ϕd(−cosϕ) =− A |
cos3 ϕ |
|
2π |
|
|
= − |
A |
|
(1−1)= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫∫yx2 dS2 = ∫∫yx2 dxdy = |
2∫πsinϕ cos2 ϕdϕ∫2 r 4 dr = − |
32 |
|
cos3 ϕ |
|
2π |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S2 |
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
5 |
|
3 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∫∫zγ (x, y, z)dS |
|
|
|
|
|
∫∫zx2 dS |
|
|
|
|
∫∫zx2 dS1 + ∫∫zx2 dS2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
zc = |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
S |
|
|
|
|
|
|
|
|
= |
|
S1 |
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫∫ |
zx2 dS = / z = 2 − |
1 |
|
(x2 + y2 ) / = |
∫∫ |
(2 − |
1 |
(x2 + y2 ))x2 |
1+ x2 + y2 dxdy = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=• |
|
• x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π,• |
|
• |
= ∫∫ |
(2 − |
1 |
r 2 )r 2 |
|
cos2 |
ϕ 1+ r 2 rdrdϕ = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y = r sinϕ, dxdy = rdrdϕ |
|
|
|
|
|
|
|
|
|
|
|
S1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2π |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
∫cos2 ϕdϕ∫(2r3 − |
r5 ) |
1+ r 2 dr. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫2 r3 |
|
|
|
1+ r 2 dr = |
|
10 |
|
|
|
|
5 |
|
+ |
2 |
|
|
|
(см. раньше). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
106
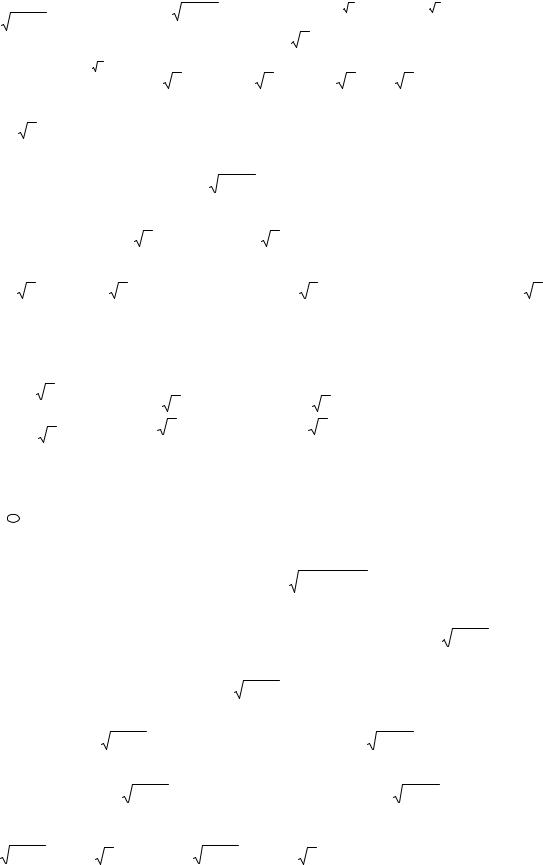
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
1+ r 2 = t 2 ,t = 1+ r 2 , r = 0,t =1, |
|
|
|
|
• |
|
|
|
|
5 |
|
|
|
|
|
|
5 |
(t 6 − 2t 4 +t)dt = |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫r5 |
|
|
1+ r 2 dr= |
|
|
|
|
• r |
2 |
|
|
= t |
2 |
|
−1,2/rdr = 2/tdt, r = 2,t = |
|
|
5 • |
|
|
= ∫(t 2 −1)ttdt = ∫ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5 |
|
|
|
−1)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
7 |
|
|
|
2 |
|
5 |
|
|
|
|
t |
3 |
|
|
|
|
|
|
5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
125 |
|
|
5 |
|
1 |
|
2 |
|
1 |
|
||||||||||||||||||||||||
= |
t |
|
|
|
− |
t |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
5 −1) − |
|
|
|
|
|
|
|
|
|
5 −1) |
+ |
|
|
|
|
|
−10 + |
− |
+ |
− |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(125 |
|
|
|
|
|
|
(25 |
|
|
|
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
7 |
|
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
7 |
|
|
|
5 |
|
|
|
3 |
|
|
|
7 |
|
|
7 |
5 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||
= |
200 |
|
|
5 |
− |
|
8 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
21 |
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫∫zx |
|
dS1 |
= |
|
|
∫cos |
|
|
ϕdϕ∫ |
2r |
|
− |
|
|
r |
|
|
|
|
1+ r |
|
|
|
dr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π1+ cos 2ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
200 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
2 |
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
15 |
2 |
|
21 |
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= |
20 |
|
|
|
|
|
+ |
|
4 |
|
|
− |
100 |
|
|
|
|
|
+ |
4 |
|
ϕ |
+ |
|
sin 2ϕ |
|
2π |
= |
|
|
|
|
20 |
|
− |
100 |
+ |
4 |
+ |
|
|
|
4 |
|
40 |
|
|
|
32 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π = |
|
|
|
5 + |
|
|
π. |
|||||||||||||||||||||||||||||
|
|
3 |
|
|
|
15 |
|
|
21 |
|
|
|
|
|
105 |
2 |
|
|
|
|
|
|
4 |
|
|
|
|
3 |
|
|
15 |
105 |
|
|
|
105 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
21 |
|
|
|
21 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
∫∫zx2 dS2 =• |
|
• z = 0• |
|
• = 0. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
200 |
|
|
5 + |
32 |
|
|
|
|
15 |
|
|
|
|
|
|
1 |
100 |
|
5 +16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
21 |
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
z |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
≈ 0,394ед.длины. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
10 |
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
5 +62 |
|
|
|
|
105 |
|
|
|
|
7 |
|
25 |
|
5 +31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Моменты инерции Ix, Iy, Iz, Io.
I x = ∫∫(y 2 + z 2 )γ (x, y, z)dS = ∫∫(y2 + z 2 )x2 dS1 + ∫∫(y2 + z 2 )x2 dS2 .
S |
S1 |
S2 |
∫∫(y |
2 |
+ z |
2 |
)x |
2 |
dS1 = ∫∫ |
|
|
|
2 |
|
+ |
|
2 − |
1 |
(x |
2 |
+ y |
2 |
|
2 |
|
|
|
2 |
1+ x |
2 |
|
+ y |
2 |
dxdy = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
y |
|
|
|
2 |
|
|
|
) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
• |
|
|
x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
|
• |
|
|
|
|
|
2 |
sin |
2 |
ϕ + |
|
|
|
|
|
|
1 |
r |
2 |
|
2 |
|
2 |
cos |
2 |
ϕ 1+ r |
2 |
rdrdϕ = |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
y = r sinϕ, dxdy = rdrdϕ • |
|
|
= ∫∫ r |
|
|
|
|
2 − |
|
2 |
|
|
|
|
r |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
• |
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ∫∫ r |
2 |
sin |
2 |
ϕ + 4 − 2r |
2 |
|
|
|
|
r |
|
r |
2 |
|
cos |
2 |
|
1+ r |
2 |
rdrdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
+ |
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
sin |
|
|
ϕ cos |
|
|
1+ r |
|
|
drdϕ + |
∫∫cos |
|
ϕ 4r |
|
|
|
− 2r |
|
|
|
|
|
|
r |
|
|
|
|
|
1+ r |
|
drdϕ = |
|
|
||||||||||||||||||||||||||||||||||||||
= ∫∫r |
5 |
2 |
2 |
ϕ |
2 |
2 |
3 |
|
|
5 |
+ |
|
1 |
7 |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2π |
|
|
|
|
2 |
ϕsin |
2 |
|
|
|
2 |
5 |
|
|
1+ r |
2 |
dr |
|
|
|
2π |
|
|
|
|
2 |
ϕdϕ |
2 |
|
4r |
3 |
− 2r |
5 |
+ |
|
1 |
r |
7 |
|
|
1 |
+ r |
2 |
dr. |
|
|
|||||||||||||||||||||||||||||
= ∫cos |
|
|
ϕdϕ∫r |
|
|
|
|
|
+ ∫cos |
|
∫ |
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫2 r3 |
|
1+ r 2 dr |
= 10 |
5 + |
|
|
2 |
|
, |
|
|
∫2 r5 |
1+ r 2 dr = |
|
200 |
|
|
5 |
− |
|
|
|
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
15 |
|
|
|
|
|
|
|
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
107

∫2 r 7 1+ r 2 dr =• |
|
1+ r 2 = t 2 , r = 0,t =1, |
|
|
|
|
|
|
|
|
• |
|
= ∫5(t 2 −1)3 t 2 dt = ∫5(t8 −3t 6 +3t 4 −t 2 )dt = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• 2/rdr = 2/tdt, r = 2,t = |
|
|
5 • |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
9 |
|
|
|
|
3 |
|
|
7 |
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
t |
3 |
|
|
|
|
5 |
|
|
|
|
|
1 |
(625 |
|
|
|
5 −1)− |
3 |
|
|
(125 |
|
|
|
5 −1)+ |
|
3 |
(25 |
|
|
|
5 −1) |
|
1 |
(5 |
|
|
5 −1)= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
t |
|
|
|
− |
t |
+ |
|
t |
− |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 |
|
|
7 |
|
|
|
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
9 |
|
|
|
7 |
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
= |
|
|
|
625 |
− |
|
375 |
|
|
+15 − |
5 |
|
− |
1 |
|
+ |
3 |
|
|
− |
3 |
+ |
1 |
= |
1840 |
|
|
|
5 + |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
9 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
3 |
9 |
|
7 |
|
|
5 |
3 |
|
63 |
|
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2π |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
8 |
|
|
|
2π |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
8 |
|
1 |
|
2π1−cos4ϕ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
∫cos |
|
|
ϕsin |
|
ϕdϕ∫r |
|
|
|
|
|
1+ r |
|
|
dr = |
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
sin |
|
2ϕdϕ = |
|
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
dϕ = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
105 |
4 |
|
|
|
|
21 |
|
|
|
|
105 |
4 |
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
200 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
1 |
|
|
|
|
|
|
|
|
|
sin |
ϕ |
|
2π |
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
5 |
|
− |
|
|
|
|
|
|
|
|
ϕ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
5 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
21 |
|
|
|
105 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
105 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2π |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫cos |
|
ϕdϕ∫ |
|
|
4r |
|
|
|
|
|
− |
2r |
|
|
+ |
|
|
|
|
r |
|
|
|
1+ r |
|
dr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2π |
1+ cos 2ϕ |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
1 |
|
1840 |
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
4 |
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
15 |
|
21 |
|
|
|
105 |
|
4 |
|
|
|
63 |
|
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
40 |
|
|
|
400 |
|
|
|
|
1840 |
|
|
|
|
8 |
|
|
|
|
|
|
16 |
|
|
|
|
|
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
sin 2ϕ |
|
|
2π |
|
|
|
100 |
|
|
|
|
|
220 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
5 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
ϕ + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
5 |
+ |
|
|
|
|
|
|
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
3 |
|
|
|
|
21 |
|
|
|
252 |
|
|
15 |
|
105 |
|
315 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫∫(y |
2 |
+ z |
2 |
|
)x |
2 |
dS1 |
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
π |
|
|
100 |
|
|
|
|
|
|
|
|
|
|
220 |
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
100 |
|
|
|
|
|
2 |
|
|
|
220 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
+ |
|
|
|
|
|
|
|
|
π = |
|
|
5 |
|
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
π |
= |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
105 |
|
4 |
|
|
63 |
|
|
|
|
|
315 |
|
21 |
|
63 |
105 |
|
315 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
250 |
|
5 |
|
+ |
|
214 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
63 |
|
|
|
|
315 |
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
x |
|
= r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
|
• |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫∫(x |
|
|
+ z )x dS2 |
|
= ∫∫ y |
|
|
+ |
2 |
|
− |
|
|
|
|
(x |
|
|
|
+ y |
|
|
) |
|
|
|
|
x dxdy= |
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = r sinϕ,dxdy = rdrdϕ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
• |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= ∫∫ |
|
|
|
sin |
ϕ + |
|
2 − |
|
|
r |
|
|
|
|
|
cos |
ϕrdrdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫∫r5 sin2 ϕcos2 ϕdrdϕ + ∫∫cos2 ϕ |
4r3 −2r5 + |
|
1 r7 drdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2π |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
5 |
|
|
|
|
1 7 |
|
|
|
|
|
|
π r6 |
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
r6 |
|
|
r |
8 |
|
2 |
|
16 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫sin |
|
ϕcos |
|
|
ϕdϕ∫r dr + ∫cos |
|
|
ϕdϕ∫ |
|
4r |
|
|
−2r |
|
|
+ |
|
|
|
|
|
r |
|
|
dr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
+π |
|
|
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
= |
|
|
π. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
6 |
|
|
|
|
r |
|
|
3 |
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
0 |
|
|
|||||||||||||||||||
I x = |
250 |
|
|
|
|
|
|
|
|
214 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
1894 |
|
|
|
|
≈ 46,766 ед. момента инерции. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
π + |
|
|
|
|
|
|
π |
|
|
= |
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
63 |
|
|
|
|
315 |
|
|
3 |
|
|
|
|
|
63 |
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
I y = ∫∫(x2 + z 2 )x2 dS = ∫∫(x2 + z 2 )x2 dS1 + ∫∫(x2 + z 2 )x2 dS2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
108
∫∫(x |
|
|
+ z |
|
)x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
2 |
− |
|
1 |
|
(x |
|
|
|
+ y |
|
|
) |
2 |
|
|
|
|
|
|
1+ x |
|
|
|
+ y |
|
|
dxdy = |
|
x = r cosϕ, r = 2,0 ≤ϕ |
≤ 2π, |
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
2 |
dS1 = ∫∫ x |
2 |
|
|
|
2 |
|
2 |
x |
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = r sinϕ,dxdy = rdrdϕ |
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ∫∫ |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
r |
|
|
|
cos |
|
|
ϕ + |
|
2 |
− |
|
|
|
|
r |
|
|
|
|
|
|
r |
|
cos |
|
|
ϕ |
1+ r |
|
rdrdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
4 −2r |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
cos |
|
|
|
|
ϕ 1+ r |
|
|
drdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
= ∫∫ |
r |
2 |
|
2 |
|
ϕ + |
2 |
|
|
+ |
|
1 |
r |
4 |
3 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
cos |
|
|
|
ϕ 1+ r |
|
|
|
drdϕ + ∫∫cos |
|
|
|
ϕ |
|
4r |
|
|
−2r |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
1+r |
|
drdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫∫r |
5 |
4 |
|
2 |
2 |
|
3 |
5 |
+ |
1 |
7 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
• |
|
2π |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2π 1+cos2ϕ 2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+cos4ϕ |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∫cos |
|
ϕdϕ = |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
|
= |
|
|
|
|
|
∫ 1+ 2cos2ϕ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 2π |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2ο |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫ |
|
|
|
+ 2cos2ϕ |
+ |
|
|
|
|
|
|
cos4ϕ |
dϕ = |
|
|
|
|
|
|
|
|
|
ϕ +sin 2ϕ |
+ |
|
|
|
sin 4ϕ |
|
|
= |
|
|
π• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
• 4 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
8 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
220 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
100 |
|
|
|
2 |
|
|
220 |
|
|
|
550 |
|
|
|
|
|
|
202 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
|
π + |
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
|
π |
= |
|
|
|
5 |
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
π |
= |
|
|
|
|
|
|
5 + |
|
|
|
π. |
|
|
|||||||||||||||||||||||||||||||||||||
21 |
|
|
|
|
105 |
4 |
|
|
63 |
|
315 |
|
|
|
7 |
|
|
63 |
35 |
315 |
|
63 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
315 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫∫(x |
2 |
|
+ z |
2 |
)x |
2 |
dS2 |
= ∫∫ |
|
|
|
|
2 |
|
+ 2 |
− |
|
1 |
|
(x |
2 |
|
|
+ y |
2 |
) |
2 |
|
|
2 |
dxdy= |
• |
|
x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
|
• |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
y |
= r sinϕ,dxdy = rdrdϕ |
• |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ∫∫ |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫r |
5 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
∫∫cos |
2 |
|
|
3 |
|
|
|
5 |
|
1 |
|
7 |
|
|
|
|||||||||||||||||||||||||||||||
r |
|
|
|
cos |
|
|
ϕ + |
|
2 |
− |
|
|
|
|
r |
|
|
|
|
|
|
r |
|
cos |
|
|
ϕrdrdϕ |
|
cos |
|
|
ϕdrdϕ + |
|
ϕ |
4r |
|
|
−2r |
|
|
+ |
|
|
|
r |
|
drdϕ = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2π |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
5 |
|
|
1 7 |
|
|
|
|
|
|
|
3 r6 |
|
2 |
|
|
|
|
|
|
4 |
|
r6 |
|
|
|
r8 |
|
2 |
|
|
|
32 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫cos |
|
|
|
ϕdϕ∫r dr + ∫cos |
|
|
ϕdϕ∫ |
4r |
|
|
|
|
−2r |
|
+ |
|
|
|
r |
|
dr = |
|
|
π |
|
|
|
|
|
|
|
|
+π |
|
|
|
|
− |
|
|
+ |
|
|
|
|
= |
|
|
|
π. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
3 |
|
32 |
|
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 6 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
550 |
|
|
|
|
|
|
|
|
|
|
202 |
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
550 |
|
|
|
|
|
|
|
3562 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
I y |
= |
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
π |
|
|
+ |
|
|
|
|
|
|
π |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
π ≈ 96,853 ед. момента инерции. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
63 |
|
|
|
|
315 |
|
|
|
|
3 |
|
|
|
|
63 |
|
|
|
|
|
|
315 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
I z = ∫∫(x2 + y2 )x2 dS = ∫∫(x2 + y2 )x2 dS1 + ∫∫(x2 + y2 )x2 dS2 .
S |
S1 |
S2 |
∫∫(x2 + y2 )x2 dS1 = ∫∫(x2 + y2 )x2 |
1+ x2 + y2 dxdy=• |
|
x = r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
||||||||||||||||||
|
|||||||||||||||||||||
S1 |
|
|
|
|
|
|
S1 |
|
2π |
|
|
2 |
|
|
|
|
• y = r sinϕ, dxdy = rdrdϕ • |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
2 |
|
2 |
|
|
2 |
|
2 |
5 |
|
2 |
|
200 |
|
8 |
|
|||
= ∫∫r |
|
r |
|
cos |
|
ϕ |
1+ r |
|
rdrdϕ = ∫cos |
|
ϕdϕ∫r |
|
1+ r |
|
dr = |
5 − |
|
|
π. |
||
|
|
|
|
|
|
|
105 |
||||||||||||||
S1 |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
21 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫∫(x2 + y2 )x2 dS2 = ∫∫(x2 + y2 )x2 dxdy = ∫∫r 2 r 2 cos2 ϕrdrdϕ =2∫πcos2 ϕdϕ∫2 r5 dϕ = π
S2 |
S 2 |
S2 |
0 |
0 |
•
=
r 6 |
|
2 |
32 |
|
|
|
|
= |
|
π. |
|
6 |
3 |
||||
|
0 |
|
200 |
|
8 |
|
32 |
200 |
|
1112 |
|
ед. момента инерции. |
|||||
I z = |
|
5 − |
|
|
π + |
|
π = |
|
5 + |
|
|
π ≈100,174 |
||
21 |
105 |
3 |
21 |
105 |
||||||||||
|
|
|
|
|
|
|
||||||||
109
Io = ∫∫(x2 + y 2 + z 2 )x2 dS = ∫∫(x2 + y2 + z 2 )x2 dS1 + ∫∫(x2 + y2 + z 2 )x2 dS2
S |
S1 |
S2 |
|
∫∫(x |
2 |
|
+ y |
2 |
+ z |
2 |
)x |
2 |
dS1 = ∫∫ |
|
|
|
2 |
+ y |
2 |
+ |
|
|
|
|
|
|
|
1 |
(x |
2 |
+ y |
2 |
|
|
|
2 |
|
|
2 |
|
|
1+ x |
2 |
+ y |
2 |
dxdy = |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
2 − |
2 |
|
|
|
) |
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
• |
|
|
x |
= r cosϕ, r = 2,0 ≤ϕ ≤ 2π, |
|
|
|
• |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
− |
|
1 |
r |
2 |
2 |
|
2 |
|
cos |
2 |
ϕ |
|
1 |
+ r |
2 |
rdrdϕ = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|
|
|
|
y = r sinϕ, dxdy = rdrdϕ |
|
|
|
|
|
|
|
|
= ∫∫ r |
|
|
+ |
|
|
2 |
|
|
|
|
|
r |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
• |
|
|
|
|
|
• |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
= ∫∫ |
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
7 |
|
|
2 |
|
|
|||||||||||||||||||||||||||||
|
|
4r |
− r |
|
+ |
|
r |
|
|
|
|
|
ϕ |
|
|
1+ r |
drdϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4r |
|
− r |
+ |
|
|
r |
|
1+ r |
dr |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
cos |
|
|
|
|
|
|
∫cos |
|
|
ϕdϕ∫ |
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π |
|
|
10 |
|
|
|
|
|
|
|
|
2 |
|
200 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
1 1840 |
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 + |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
15 |
|
21 |
|
|
|
|
|
|
|
|
|
4 |
|
|
63 |
|
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
40 |
|
|
|
200 |
|
|
|
|
|
|
460 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
4 |
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
196 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
π |
|
|
|
5 |
|
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
+ |
|
|
|
|
|
|
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
3 |
|
|
21 |
|
|
|
63 |
|
|
|
15 |
|
105 |
315 |
|
|
63 |
|
|
|
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∫∫(x |
|
+ y |
|
|
+ z |
|
|
)x |
|
dS2 |
|
= ∫∫ |
x |
|
|
|
+ y |
|
|
+ 2 |
− |
|
|
|
|
|
(x |
|
|
+ y |
|
|
) |
|
x |
|
dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= ∫∫ |
|
|
2 |
+ |
|
− |
r |
2 |
|
|
|
|
|
2 |
cos |
2 |
ϕrdrdϕ = ∫∫ |
|
|
|
3 |
|
− r |
5 |
+ |
|
r |
7 |
|
|
|
|
|
2 |
ϕdrdϕ = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
|
|
2 |
2 |
|
|
|
|
|
|
|
r |
|
|
|
4r |
|
|
|
|
|
|
4 |
|
|
cos |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2π |
|
|
|
2 |
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
5 |
|
|
|
1 7 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
r 6 |
|
|
|
|
r8 |
|
|
|
2 |
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
= ∫cos |
|
ϕdϕ∫ |
4r |
|
|
|
− r |
|
|
|
|
|
|
r |
|
|
dr |
|
= π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
+ |
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
r |
|
6 |
|
|
32 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Io |
= |
|
700 |
|
|
5 + |
|
196 |
|
|
+ |
40 |
|
|
|
|
|
|
700 |
|
5 + |
4396 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
63 |
|
|
|
315 |
π |
|
|
3 |
|
π = |
|
|
|
63 |
|
|
315 |
|
|
π ≈121,83 ед. момента инерции. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3.5.1.5. Задание на контрольную работу
Вычислить массу, координаты центра масс и моменты инерции относительно координатных осей и начала координат материальной оболочки, которая представляет собой полую тонкостенную конструкцию, выполненную из композитного материала с поверхностной плотностью
γ (x, y, z) |
кг |
|
. Оболочка имеет вид тела, ограниченного поверхностями S1, S2, |
3 |
|||
м |
|
|
|
S3. |
|
|
|
1. |
|
γ (x, y, z)= x2 + y2 , S1 : z = x2 + y2 +1, S2 : z = 5 . |
|
110

2. |
γ (x, y, z)= z2 , |
S1 : y2 + z2 = x2 , S2 : x = 2. |
3. |
|
|
|
|
|
|
|
4.γ (x, y, z)= x2 + y2 , S1 : z =  16 − x2 − y2 , S2 : z = 0.
16 − x2 − y2 , S2 : z = 0.
5.γ (x, y, z)= x2 + y2 , S1 : 4(x2 + y2 −1)+ z = 0, S2 : z = 0.
6. |
γ (x, y, z)= 1+ 2(x2 + y2 ), S1 : x2 + y2 − z = −1, S2 : z = 2, z > 0. |
7.γ (x, y, z)= y2 , S1 : x2 + z2 = 19 y2 , S2 : y = 3, y > 0.
8.γ (x, y, z)= z, S1 : z = 14 (x2 + y2 ), S2 : z =1.
9.γ (x, y, z)= y2 , S1 :1− z = x2 + y2 , S2 : z = 0.
10.γ (x, y, z)= z 2 , S1 : x2 + y2 = 4, S2 : y = −2, S3 : y = 2.
3.5.2.Поверхностный интеграл II рода
3.5.2.1.Определение
Поверхностный интеграл II рода от векторной функции (поля) F (x, y, z)
по ограниченному куску гладкой двухсторонней поверхности называется предел интегральной суммы:
n |
|
|
|
|
|
||||
n→∞lim ∑ |
|
(xi , yi , zi ) |
|
i |
Si = ∫∫ |
|
(x, y, z) |
|
|
F |
n |
F |
ndSi , где |
||||||
max S →0 i=1 |
σ |
||||||||
F (x, y, z) = Fx (x, y, z)i + Fy (x, y, z) j + Fz (x, y, z)k - векторная функция (поле)
определённая на ограниченном куске гладкой двухсторонней поверхности σ
(рис. 3.30),
Si – площадь i-ой элементарной площадки, на которые разбит весь кусок поверхности σ, ( i =1, n ). Элемент Si, как бесконечно малый участок кривой поверхности σ, можно с точностью до малых высшего порядка считать плоским,
111
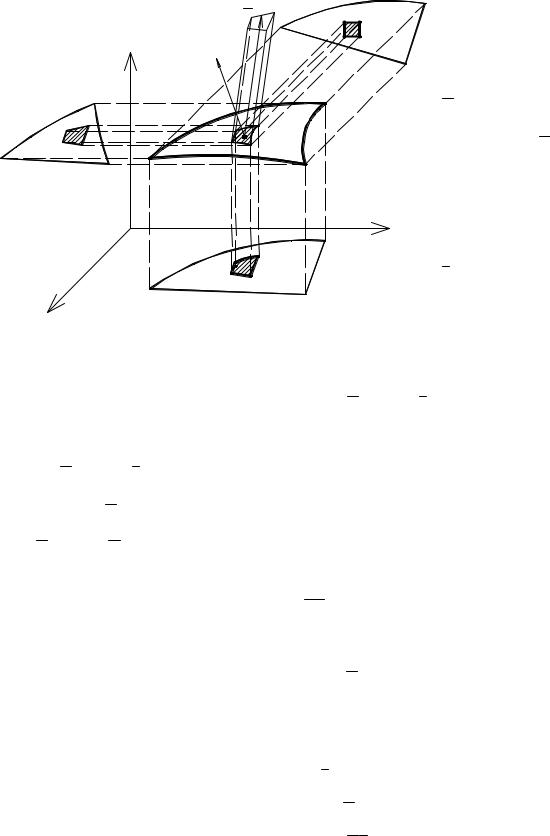
|
|
F |
σzy |
dy |
n |
– |
|
количество |
z |
|
|
dz |
|
|
элементарных |
||
|
ni |
|
|
|
|
|||
|
|
|
площадок, |
|
||||
|
|
|
|
|
|
|||
dz |
|
Si |
σ |
|
F(xi , yi , zi ) |
- |
значение |
|
|
|
|
функции |
F в точке |
||||
σxz dx |
|
|
|
|
||||
|
|
|
|
|
(xi,yi,zi), принадлежащей |
|||
|
|
|
|
y |
элементарной площадке |
|||
|
|
|
|
Si, |
|
|
|
|
x |
|
σxy dy dx |
|
|
ni - |
|
|
единичный |
|
|
|
|
нормальный |
вектор к |
|||
|
|
Рис. 3.30 |
|
|
поверхности σ в точке |
|||
|
|
|
|
(xi,yi,zi). |
|
|
||
|
|
|
|
|
|
|
||
Скалярное произведение векторов ( F(xi , yi , zi )ni ) есть высота цилиндра с |
||||||||
основанием Si (рис. 3.30), |
|
|
|
|
|
|
||
F(xi , yi , zi )n Si |
- объём указанного цилиндра. |
|
|
|
|
|||
Если F (x, y, z) |
- скорость жидкости, протекающей через поверхность σ, |
|||||||
то F(xi , yi , zi )ni |
Si - |
количество жидкости, протекающей через элементарную |
||||||
площадку Si |
в единицу времени м3 |
или расход жидкости, ещё проще – |
||||||
|
|
|
с |
|
|
|
|
|
поток жидкости. Тогда интегральная сумма – приближенное значение, а её предел – точное значение потока вектора F через всю поверхность.
Физический смысл поверхностного интеграла II рода – это есть количество жидкости, протекающей в единицу времени (расход, поток) через поверхность σ в направлении вектора n . Поэтому поверхностный интеграл II рода называют потоком векторного поля F через поверхность σ.
П = ∫∫F ndS .
σ
112
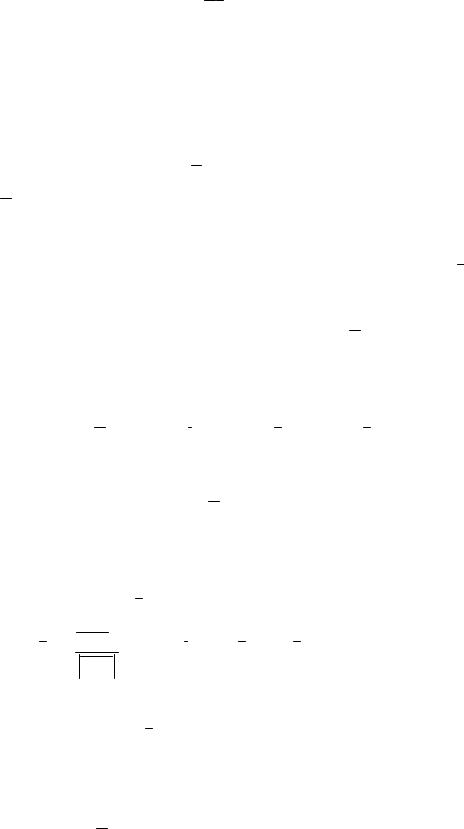
Скалярное произведение векторов ( Fn ) образует скалярную функцию f (x, y, z) и тогда поверхностный интеграл II рода преобразуется в
поверхностный интеграл I рода.
3.5.2.2. Вычисление поверхностного интеграла II рода
При определении потока вектора F через поверхность σ как правило задают: вектор F , поверхность σ (уравнение) и сторону двухсторонней поверхности. σ, через которую проходит поток. Последнее условие обычно кратко формулируется направлением единичного нормального вектора n к внутренней или внешней стороне поверхности σ: нормаль внутренняя или внешняя. От этого условия зависит знак потока вектора F , что отличает поверхностный интеграл II рода от поверхностного интеграла I рода.
Расчёт потока вектора сводится к вычислению двойного интеграла. Пусть векторное поле F = Fx (x, y, z)i + Fy (x, y, z) j + Fz (x, y, z)k. Поверхность
σ задана уравнением z = z(x, y) или ϕ(x, y, z)= z − z(x, y) = 0 .
Требуется найти поток П вектора F через поверхность σ, нормаль внешняя (внутренняя).
Воспользуемся формулами (3.11), приведёнными в 3.5.1.2, для единичного нормального вектора n к поверхности σ:
n= ± gradgradϕ = ±(cosαi + cos β j + cosγ k)
атакже формулами (3.12-3.15),устанавливающие связь направляющих косинусов cosα, cosβ, cosγ вектора n с элементами интегрирования dx, dy, dz, dS:
dxdy = cosγdS , dydz = cosαdS , dxdz = cos βdS . |
(3.16) |
Тогда поток П вектора F равен:
113

П = ∫∫F ndS = ∫∫(Fx (x, y, z)i + Fy (x, y, z) j + Fz (x, y, z)k)(±)(cosαi + cos β j + cosγ k)dS =
σσ
=±∫∫Fx (x, y, z) cosαdS + Fy (x, y, z) cos βdS + Fz (x, y, z) cosγdS =
σ
= ±∫∫Fx (x, y, z)dydz + Fy (x, y, z)dxdz + Fz (x, y, z)dxdy.
σ
По последнему виду интеграла поток вектора ещё называют поверхностным интегралом по координатам.
При расчёте потока вектора эту формулу нужно понимать так:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫Fx (x, y, z)dydz +∫∫Fy (x, y, z)dxdz + ∫∫Fz (x, y, z)dxdy |
|
(3.17) |
||
|
|
|
|||||||
П = ∫∫F ndS = ± |
|
||||||||
σ |
|
|
|
|
σ yz |
σxz |
σxy |
|
|
Здесь σyz, σxz, σxy есть проекции поверхности σ на соответствующие координатные плоскости (рис. 3.30). Обязательным условием применения формулы (3.17) для расчёта потока вектора является однозначность проектирования поверхности σ на координатные плоскости.
Если это условие нарушается, нужно поверхность σ разделить на куски σ1, σ2,…σm, удовлетворяющие этому условию и расчёт потока вектора производить по каждому из этих кусков поверхности, а затем суммировать (см. введение, общее свойство 3).
Например, для расчёта потока вектора через поверхность S1 (рис. 3.29) по формуле (3.17) нужно данную поверхность разделить на 4 части (по октантам) и в каждой из них вычислить три двойных интеграла, т.е. всего требуется вычислить 12 интегралов.
При этом необходимо правильно выбрать знак + или – перед интегралом.
Ниже приводится формула, позволяющая, например, для данного случая (рис. 3.29) рассчитать поток вектора только по одному двойному
интегралу. |
|
|
|
|
||
Перепишем формулы (3.16) в следующем виде: |
|
|||||
dS = |
dydz |
, dS = |
dxdz |
, dS = dxdy . |
(3.18) |
|
cosα |
cos β |
|||||
|
|
cosγ |
|
|||
114

Подставим формулы (3.18) в общую формулу для потока вектора:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dydz |
|
|
|
|
|
|
|||
|
|
|
|
∫∫F n |
|
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
cosα |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
σ yz |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dxdz |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.19) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
П = ∫∫F ndS = ∫∫F n |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
cos β |
|
|
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
σ |
|
|
|
σxz |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|||||||||
|
|
|
|
∫∫F n |
|
|
|
. |
|
||||||||||||||||
|
|
|
|
|
|
cosγ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Это и есть необходимые для расчёта формулы.
Замечание. Элемент интегрирования dS есть площадь бесконечномалой элементарной площадки, которая всегда положительная. Чтобы сохранить это обстоятельство в расчётной формуле при замене dS на соответствующие элементы интегрирования dx, dy, dz (положительные бесконечно-малые длины) и направляющие косинусы cosα, cosβ, cosγ по формулам (3.18), данные косинусы должны быть взяты по модулю.
Правила расчёта потока вектора
• По условиям задачи построить чертёж (рисунок) поверхности σ и по нему определить координатную плоскость, на которую поверхность σ проектируется однозначно. Этим самым выбирается одна из трёх формул (3.19) и область интегрирования сформированного в дальнейшем двойного интеграла.
Если поверхность σ однозначно проектируется на несколько координатных плоскостей, то от выбора одной из них может зависеть эффективность (простота) расчёта. Иногда могут встретиться случаи, когда неудачный выбор координатной плоскости приводит к неберущемуся интегралу, а удачный выбор разрешает все проблемы.
•По заданному уравнению поверхности σ найти единичный,
нормальный вектор n к этой поверхности по формуле (3.11).
115

Здесь же определяются конкретные значения для направляющих косинусов, которые могут быть как числами, так и аналитическими выражениями.
• Определить знак + или – для единичного, нормального вектора n , найденного по формуле (3.11). Для чего:
По условию задачи (нормаль внешняя или внутренняя) на рисунке построить вектор n ;
По рисунку определить знак того направляющего косинуса, который находится в выбранной формуле (3.19). Угол (α, β или γ) этого
косинуса будет острым или тупым и сохраняться при перемещении вектора n по всей поверхности σ, а значит и знак этого косинуса будет сохраняться по всей этой поверхности;
Выбрать знак + или – перед аналитическим выражением вектора n (3.11) таким, чтобы знак направляющего косинуса, определённого в предыдущем пункте, совпадал со знаком этого косинуса в формуле для n .
•Подставить значения F и n в формулу (3.19), произвести скалярное перемножение этих векторов, привести интеграл к двойному интегралу и рассчитать его. Если в подынтегральном выражении встречается переменная, не участвующая в интегрировании, то её нужно выразить через переменные интегрирования, используя уравнение поверхности σ. При необходимости двойной интеграл можно вычислить в полярной системе координат.
3.5.2.3. Некоторые приложения поверхностного интеграла II рода
Поверхностный интеграл II рода непосредственно применяется для вычисления потока вектора, о чём говорилось в 3.5.2.1. В тоже время, в формулах Остроградского-Гаусса и Стокса он нашёл применение как в самом анализе, так и в его приложениях, в частности, в теории поля.
116
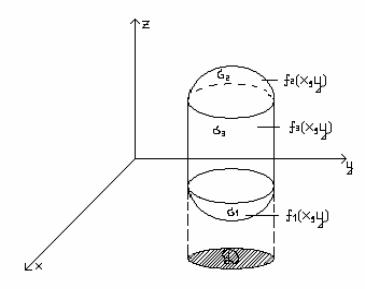
Отступая от традиционного изложения пособия, когда теоретические сведения давались в кратком виде, автор посчитал, что формулы Остроградского-Гаусса и Стокса необходимо дать в более развернутом виде, то есть доказать их, тем более, что в современной литературе эти доказательства несколько сокращены, недосказаны, а порой и непонятны студентам.
Ниже автор делает попытку доказать эти формулы с учетом этих обстоятельств.
Формула Остроградского-Гаусса (1828 г.)
Формула Грина устанавливает связь между криволинейным интегралом II рода по замкнутому контуру и двойным интегралом по плоской области, ограниченной этим контуром.
Аналогично связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по области, ограниченной этой поверхностью, устанавливает формула Остроградского-Гаусса.
Рис. 3.31
117
Пусть в пространстве задана трехмерная область V, ограниченная замкнутой поверхностью δ, проецирующаяся на плоскость xOy в выпуклую (правильную) двухмерную область D (рис 3.31),
Положим, что δ= δ1+ δ 2+ δ3, где поверхность δ1:Z=f1(x;y), δ2:Z=f2(x;y),
δ3:Z=f3(x;y), причем поверхность δ3- цилиндр, образующая которой параллельна оси Оz.
В подынтегральное выражение поверхностного интеграла II рода
|
|
|
|
|
_ |
_ |
|
|
|
|
|
|
|
|
П= ∫∫F n ds входит векторная функция (поле) |
||||||
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
|
_ |
|
_ |
|
|
_ |
_ |
|
|
|
|
F = |
Fx (x, y, z) i + Fy (x, y, z) j+ Fz (x, y, z) k . |
|||||
|
Формально (без всяких объяснений и причин) преобразуем тройной |
|||||||||
интеграл по области |
V от функции ∂Fz (x, y, z) |
к двойному интегралу по |
||||||||
|
|
|
|
|
|
|
|
∂z |
|
|
проекции D. |
|
|
|
|
|
|
||||
∫∫∫∂Fz (x, y, z) |
dxdydz =∙│∙ |
выделим внутренний интеграл по z ∙│∙= |
||||||||
V |
∂z |
|
|
|
|
|
|
|
|
|
= ∫∫( |
f ( x |
, y) |
∂Fz (x, y, z)dz)dxdy = ∙│∙ подынтегральное выражение внутреннего |
|||||||
2 ∫ |
|
|||||||||
D f1 ( x, y) |
|
∂z |
|
|
|
|
|
|
||
интеграла есть частный дифференциал функции Fz (x, y, z) по z∙│∙= |
||||||||||
|
f ( x, y) |
|
|
|
|
|
|
|
|
|
= ∫∫( |
2 ∫d z F (x, y, z))dxdy = ∫∫(Fz (x, y, z) |
|
ff12((xx,,yy)) )dxdy = |
|
||||||
|
|
|||||||||
D f1 ( x, y) |
|
|
|
D |
|
|
|
|
||
∫∫[Fz (x, y, f2 (x, y) − Fz (x, y, f1 (x, y))]dxdy = |
|
|
||||||||
D |
|
|
|
|
|
|
|
|
|
|
∫∫[Fz (x, y, f2 (x, y))]dxdy − ∫∫[Fz (x, y, f1 (x, y))]dxdy = |
|
|
||||||||
D |
|
|
|
|
D |
|
|
|
|
|
=∙│∙Заменим область интегрирования D на соответствующие кривые |
||||||||||
поверхности δ1 и δ 2∙│∙ = |
|
|
||||||||
|
= ∫∫Fz (x, y, z)dxdy − ∫∫Fz (x, y, z)dxdy = |
|
|
|||||||
|
|
δ2 |
|
|
δ1 |
|
|
|||
=∙│∙ |
воспользуемся одной из формул (3.16) |
dxdy = cos γds = cos(n, Oz)ds .Угол γ |
||||||||
есть угол между осью Оz и единичным нормальным вектором к |
||||||||||
соответствующей кривой поверхности ∙│∙ = |
|
|
||||||||
|
= ∫∫Fz (x, y, z) cos(n2 ,Oz)ds − ∫∫Fz (x, y, z) cos(n1,Oz)ds = |
|||||||||
|
|
δ2 |
|
|
δ1 |
|
|
|||
118

=∙│∙ заметим что угол (n2 ,Oz) острый, значит его косинус положительный, и данное слагаемое знак не меняет по всей поверхности δ2 . Угол (n1 ,Oz) тупой, значит его косинус отрицательный, и второе слагаемое меняет знак.
Прибавим к этой сумме 0= ∫∫Fz (x, y, z) cos (n3 ,Oz)ds Этот 0 получается в
δ3
результате того, что угол (n3 ,Oz) - прямой всюду, а значит cos (n3 ,Oz) = 0 ∙│∙=
= ∫∫Fz (x, y, z) cos(n2 ,Oz)ds + ∫∫Fz (x, y, z) cos(n1,Oz)ds + ∫∫Fz (x, y, z) cos(n3 , z)ds =
δ2 δ1 δ3
=∙│∙ данная сумма означает интегрирование одной и той же функции
Fz (x, y, z) по замкнутой поверхности δ = δ1 +δ2 +δ3 |
∙│∙= ∫∫Fz (x, y, z) cos( |
|
,Oz)ds. |
||||
n |
|||||||
|
|
|
|
|
δ |
||
Итак ∫∫∫∂Fz (x, y, z) |
= ∫∫Fz (x,y, z) cos( |
|
,Oz)ds.. |
|
|
|
|
n |
|
|
|
||||
V |
∂z |
δ |
|
|
|
||
Рассуждая аналогичным образом можно придти к формулам:
∫∫∫∂Fx (x, y, z)dxdydz = ∫∫Fx (x, y, z) cos( |
|
|
,Ox)ds |
||||
n |
|||||||
V |
∂x |
δ |
|||||
∫∫∫ |
∂Fy (x, y, z) |
dxdydz = ∫∫Fy (x, y, z) cos( |
|
,Oy)ds . |
|||
n |
|||||||
∂y |
|||||||
V |
δ |
||||||
Складываем левые и правые части полученных формул.
∫∫∫( |
∂F (x, y, z) |
+ |
∂Fy (x, |
y, z) |
+ |
∂F (x, y, z) |
)dxdydz = |
x |
|
|
z |
||||
∂y |
|
||||||
V |
∂x |
|
|
|
∂z |
|
= ∫∫[Fx cos(n,Ox) + Fy cos(n,Oy) + Fz cos(n,Oz)]ds .
δ
Это развернутая формула Остроградского-Гаусса. Её можно переписать, автоматически понимая, что координаты векторной функции (поля) F есть скалярные функции трех переменных:
|
∂F |
∂Fy |
|
∂F |
|
|
∫∫∫( |
x + |
|
+ |
z )dxdydz = ∫∫Fxdydz + Fy dxdz + Fz dxdy . |
||
∂y |
||||||
V |
∂x |
|
∂z |
δ |
||
Здесь учтены формулы (3.16).
Видно, что в правой части сосредоточен поверхностный интеграл II родапоток вектора F через всю замкнутую поверхность δ.
119
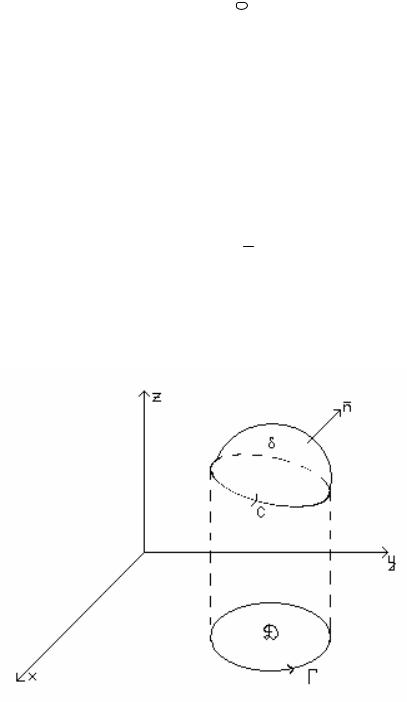
|
|
|
|
|
Если |
в |
|
левой |
части |
формулы |
выражение |
|||||||||||||||||||
|
∂F |
∂Fy |
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x |
+ |
|
+ |
|
|
z |
= divF обозначить как |
дивергенция |
векторного |
поля |
F , |
то |
|||||||||||||||
|
|
|
|
∂y |
|
|
|
|||||||||||||||||||||||
|
|
∂x |
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
формулу Остроградского-Гаусса можно записать сокращенно: |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫∫divF |
= ∫∫Fnds . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
δ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Прокомментируем формулу Остроградского-Гаусса. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Формула |
применяется при условии, что |
векторная функция(поле) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
должна быть непрерывна вместе с |
||||||||||||||||||||
|
|
F |
= Fx (x, y, z)i |
+ Fy (x, y, z) j + Fz (x, y, z)k |
||||||||||||||||||||||||||
частными |
производными первого |
порядка от координатных функций в |
||||||||||||||||||||||||||||
пространственной области V, ограниченной замкнутой поверхностью δ. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
Тогда тройной |
интеграл от |
дивергенции |
векторного |
поля |
|
|
|
|
по |
||||||||||||||||
|
|
|
|
|
|
F |
||||||||||||||||||||||||
некоторому объему равен потоку вектораF через замкнутую поверхность, ограничивающую данный объем.
Формула Стокса (1854 г.)
Рис. 3.32
Пусть в трехмерном пространстве задан кусок непрерывной кривой поверхности δ, описываемой формулой z = z(x, y) . С – кривая,
120
ограничивающая поверхность δ. D = δxy – проекция поверхности δ на
плоскость xOy. |
|
|
|
|
|
|
|
|
||||
|
|
Г- проекция кривой С на плоскость xOy (рис 3.32) . |
|
|||||||||
|
|
Прежде |
чем |
заставить |
циркулировать |
вектор |
||||||
|
|
|
|
|
|
|
|
|
формулу |
|||
|
F |
= Fx (x, y, z)i |
+ Fy (x, y, z) j + Fz (x, y, z)k по контуру С и доказывать |
|||||||||
Стокса, приведем два необходимых для этой цели предварительных сведения.
Сведение 1. В дифференциальном исчислении функции нескольких переменных существует формула полной производной.
|
Если θ =θ(x(t), y(t), z(t)), то θt' = |
dθ |
= |
∂θ |
|
dx |
+ |
|
∂θ dy |
+ |
∂θ |
|
dz |
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
dt |
∂x dt |
|
∂y dt |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z dt |
||||||||||
|
Здесь используем частный случай формулы полной производной. |
||||||||||||||||||||||||||||||||
|
Если Fz = Fz (x, y, z) = Fz (x, y, z(x, y)), где x,y- |
независимые переменные, а z |
|||||||||||||||||||||||||||||||
зависит |
от |
|
|
x |
|
,y, |
|
т.к. это уравнение |
поверхности (z=z(x y)), то |
||||||||||||||||||||||||
(F )' |
= |
|
∂Fz |
|
dx |
+ |
∂Fz |
|
dy |
+ |
∂Fz |
∂z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
z x |
|
|
|
∂x |
|
dx |
|
|
∂y dx |
|
∂z ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∙ |
dx |
|
|
|
dy |
|
= 0 -x,y- независимые переменные |
∙ |
|
|
|
|
|
||||||||||||||||||||
= │∙ |
|
|
=1; |
|
|
|
|
|
│∙ = |
|
|
|
|
|
|||||||||||||||||||
dx |
dx |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
= |
|
∂Fz |
+ |
|
∂Fz |
∂z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
||||||||||||
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналогичные рассуждения относятся к другим функциям.
Fy = Fy (x, y, z); (Fy )'x = |
∂Fy |
|
dx |
+ |
|
∂Fy |
|
dy |
+ |
|
|
∂Fy |
|
∂z |
= |
|
|
∂Fy |
+ |
|
∂Fy |
|
∂z |
; |
|
* |
||||||||||||||||||||||
∂x dx |
|
∂y dx |
|
|
∂z ∂x |
|
|
∂x |
|
∂z |
|
∂x |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Fx = Fx (x, y, z); (Fx )'y = |
∂Fx |
|
dx |
|
+ |
|
∂Fx |
|
dy |
|
+ |
|
∂Fx |
|
∂z |
|
= |
|
∂Fx |
|
+ |
∂Fx |
|
∂z |
|
; |
|
* |
||||||||||||||||||||
∂x dy |
|
∂y dy |
|
|
∂z ∂y |
|
|
∂y |
|
∂z ∂y |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Fz = Fz (x, y, z(x, y)); (Fz )'y = |
|
∂Fz |
|
dx |
+ |
|
∂Fz |
|
dy |
+ |
|
∂Fz |
|
∂z |
= |
|
∂Fz |
+ |
|
∂Fz |
|
∂z |
.* |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z ∂y |
||||||||||||||||||||||||||||
|
|
|
|
|
|
∂x dy |
|
∂y dy |
|
∂z ∂y |
|
∂y |
|
|
||||||||||||||||||||||||||||||||||
Обозначим все четыре необходимые в будущем формулы одной звездочкой.
Сведение 2. Уравнение поверхности Z=z(x,y) можно переписать в виде φ(x,y,z) =z-z(x,y)=0. Тогда можно определить единичный нормальный вектор
121

к этой поверхности как |
n = ± |
gradϕ |
|
. Знак перед дробью выбираем +, |
|
/ gradϕ |
/ |
||||
|
|
|
используя направление циркуляции вектора по контуру С как показано на рисунке (3.32) , направление вектора n от внешней стороны поверхности δ и правило правого винта.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ∂z |
|
|
|
|
|
|
|
− |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
gradϕ |
|
|
|
ϕx' i |
|
+ϕy' |
j |
+ϕz' k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
1 |
|
|
|
||||||||||
n = |
|
= |
= |
|
|
|
|
|
|
|
|
|
∂x |
|
i + |
|
|
|
|
|
|
j + |
k = |
||||||||||||||||||||||||
/ gradϕ |
/ |
|
|
/ gradϕ / |
|
|
|
|
|
|
|
|
|
/ gradϕ / |
|
/ gradϕ |
/ |
|
/ gradϕ / |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= cos(n,Ox)i |
+ cos(n,Oy) j + cos(n,Oz)k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Тогда направляющие косинусы будут выражаться: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
− |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
− ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
cos(n,Ox) = |
|
|
|
, |
|
cos(n,Oy) = |
|
|
∂y |
, |
cos(n,Oz) = |
|
|
1 |
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||
/ gradϕ / |
|
|
/ gradϕ / |
|
/ gradϕ / |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
С другой стороны, воспользуемся |
|
еще |
|
раз |
формулами (3.16) |
||||||||||||||||||||||||||||||||||||||||||
dxdy = cos γds = cos(n,Oz)ds , |
|
|
|
dydz = cosαds = cos(n, Ox)ds , dxdz = cos βds = cos(n, Oy)ds . |
|||||||||||||||||||||||||||||||||||||||||||
Откуда cos(n,Ox) = |
dydz |
|
, cos(n,Oy) = |
dxdz |
, cos(n,Oz) = |
dxdy |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Приравняем правые части для соответствующих равных левых частей:
− |
∂z |
|
|
|
− |
∂z |
|
|
dxdz |
|
|
|
|
|
∂x |
= |
dydz |
; |
∂y |
= |
; |
1 |
= |
dxdy |
. |
||||
/ gradϕ / |
|
ds |
|
/ gradϕ / |
|
ds |
|
/ gradϕ / |
|
ds |
|
|||
Последнее уравнение дает значение / gradϕ / = dxdyds , которое подставим
|
∂z |
|
|
|
− |
∂z |
|
|
|
|
|
|
− ∂x |
|
|
|
|
|
|
= |
dxdz |
|
|
в оставшиеся два уравнения: |
|
= dydz |
; |
∂y |
|
; откуда |
|||||
|
ds |
|
ds |
|
ds |
|
|
ds |
|
||
|
dxdy |
|
|
|
dxdy |
|
|
|
|
||
− ∂∂xz = dxdz , − ∂∂yz = dydz ** .
Обозначим эти необходимые формулы двумя звездочками ** .
Доказательство формулы Стокса.
122

|
Рассмотрим циркуляцию вектора |
|
по контуру С: |
|
|
|
|
||||||||||||||||||||||||||||||||
|
F |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Ц= ∫ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
Fdl = ∫ Fx (x, y, z)dx + Fy (x, y, z)dy + Fz (x, y, z)dz = |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
∂z |
|
|
|
∂z |
|
|
По данной замене переменной z на переменные |
||||||||||||||||||||||||
│∙z = z(x, y); dz = |
∂x dx |
+ |
|
dy |
|||||||||||||||||||||||||||||||||||
∂y |
|||||||||||||||||||||||||||||||||||||||
x и y |
осуществляется переход циркуляции вектора |
|
|
по плоскому контуру |
|||||||||||||||||||||||||||||||||||
F |
|
||||||||||||||||||||||||||||||||||||||
Г∙│∙ |
|
= ∫Fx [x, y, f (x, y)]dx + Fy [x, y, f (x, y)]dy + Fz [x, y, f (x, y)](∂z dx + |
∂z dy) = |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
∫[Fx (x, y, f (x, y)) + Fz |
(x, y, f (x, y)) |
∂z]dx +[Fy (x, y, f (x, y)) + Fz (x, y, f (x, y)) |
∂z]dy = |
||||||||||||||||||||||||||||||||||||
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
∂Q |
|
|
|
∂P)dxdy . |
|
∂y |
|||||
=∙│∙Напомним формулу Грина: ∫Pdx + Qdy = ∫∫( |
− |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
D |
|
∂x |
|
|
|
∂y |
|
|
|
|
|||
|
Используем формулу Грина в интересах доказательства формулы |
||||||||||||||||||||||||||||||||||||||
Стокса∙│∙ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= ∫∫[(Fy (x, y, f (x, y)) + Fz (x, y, f (x, y)) |
∂z )'x −(Fx (x, y, f (x, y)) + |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
+F (x, y, f (x, y)) |
∂z )' ]dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
z |
|
|
|
|
|
∂x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
=∙│∙При дифференцировании функций Fx , Fy , Fz воспользуемся |
||||||||||||||||||||||||||||||||||||||
формулами * ∙│∙ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= ∫∫D ( |
∂Fy |
∂Fy ∂z |
∂F ∂z |
|
∂F ∂z ∂z |
|
|
|
∂2 z |
∂F |
− |
∂F ∂z |
∂F ∂z |
∂F ∂z ∂z |
|||||||||||||||||||||||||
∂x + |
|
∂z ∂x |
+ ∂x ∂y |
+ ∂z ∂x ∂y |
+ Fz ∂x∂y |
− ∂y |
|
∂z ∂y |
− ∂y ∂x |
− ∂z |
∂x ∂y − |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
z |
z |
|||||
|
|
|
∂2 z |
|
|
|
|
|
∂F |
|
∂Fy |
|
∂z |
|
|
∂F |
∂F |
|
∂z |
|
|
|
∂Fy |
|
∂F |
∙ |
|||||||||||||
− Fz |
|
|
|
|
)dxdy |
= ∫∫[( |
|
|
|
z − |
|
)(− |
|
|
) +( |
|
x − |
|
z )(− |
|
|
) +( |
|
|
|
− |
x )]dxdy = = |
│∙ По |
|||||||||||
|
∂x∂y |
|
|
|
∂z |
∂x |
|
|
∂y |
|
∂x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
D |
∂y |
|
|
|
|
∂z |
∂x |
|
|
|
|
|
|
∂y |
|
|
|||||||||||||||||
формулам **, заменим частные производные на соответствующие отношения дифференциалов, при этом интегрирование по плоской области D нужно заменить на интегрирование по кривой области δ, т.к. появляется третья переменная z∙│∙ =
= ∫∫[( |
∂F |
|
∂Fy |
|
dz |
|
∂F |
|
|
∂F |
|
dz |
|
∂Fy |
|
∂F |
)]dxdy |
|
||||
z − |
|
|
) |
|
+( |
x − |
z ) |
|
|
+( |
|
− |
x |
= |
||||||||
|
∂z |
dx |
dy |
∂x |
||||||||||||||||||
δ |
|
∂y |
|
|
|
|
∂z |
|
|
∂x |
|
|
|
∂y |
|
|
|
|||||
|
∂F |
|
|
∂Fy |
|
|
|
|
∂F |
|
|
∂F |
|
|
|
∂Fy |
|
∂F |
||||
= ∫∫( |
|
z |
− |
|
|
|
)dydz + |
( |
|
x |
− |
|
z )dxdz + ( |
|
− |
x )dxdy . |
||||||
|
|
∂z |
|
|
∂x |
|||||||||||||||||
δ |
|
∂y |
|
|
|
|
|
|
∂z |
|
|
∂x |
|
|
|
|
∂y |
|||||
123

Получили развернутую формулу Стокса:
|
|
∂F |
∂Fy |
|
∂F |
∂F |
∂Fy |
|
∂F |
|
∫Fx dx + Fy dy + Fz dz = ∫∫( |
z − |
|
)dydz + ( |
x − |
z )dxdz + ( |
|
− |
x )dxdy . |
||
∂z |
∂x |
|||||||||
c |
δ |
∂y |
|
∂z |
∂x |
|
∂y |
|||
Ее можно записать в сокращенном виде.
Слеваизвестная развернутая формула циркуляции вектораF ,которую
сокращенно можно записать: Ц= ∫Fdl .
c
Интеграл справа можно представить как поток пока еще неопределенного вектора по поверхности δ.
Рассмотрим специальный вектор, называемый ротор (вихрь) вектора
|
|
, обозначаемый |
в |
|
|
|
|
||||||||||||
|
F |
|
сокращенном виде rotF |
и представляемый |
|||||||||||||||
определителем III порядка:. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
||
|
|
|
|
|
i |
|
|
|
j |
|
|
|
|
|
|||||
|
|
|
|
|
∂ |
|
∂ |
|
∂ |
|
, где первая строка определителя есть единичные |
||||||||
|
|
rotF |
= |
||||||||||||||||
|
|
∂x |
|
∂y |
|
∂z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Fx |
|
Fy |
|
Fz |
|
|
|
|
||||||
орты i ; j : k ; вторая строка – символические частные производные, в которых указано по какой переменной производится дифференцирование, без указания какая функция дифференцируется; третья строкакоординатные функции трех переменных исходного вектора(векторной функции, поля). Получить развернутую формулу rotF можно по правилу расчета определителя III порядка по элементам первой строки, при этом в соответствующих минорах второго порядка, вместо соответствующих диагональных произведений, нужно произвести частное дифференцирование соответствующей координатной функции вектора F (подставить в числитель частной производной недостающую функцию для дифференцирования).
124

Например, для обычного минора: |
|
a11; a12 |
= a |
a |
22 |
− a a |
21 |
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
a21; a22 |
11 |
|
12 |
|
||
|
∂ |
; |
∂ |
|
|
∂F |
|
∂Fy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
для нашего минора: |
∂y |
∂z |
= |
− |
. |
|
|
|
|
|
|
||||||
|
z |
|
|
|
|
|
|
|
|
||||||||
|
∂y |
∂z |
|
|
|
|
|
|
|||||||||
|
Fy ; Fz |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
k |
|
|
|
∂ |
|
|
; |
∂ |
|
|
|
|
∂ |
|
; |
|
∂ |
|
|
|
|
|
|
|
|
∂ |
; |
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
∂ |
|
∂ |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
∂y |
∂z |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
rotF |
|
|
|
|
|
i |
+ |
∂z |
|
|
|
∂x |
|
|
j |
+ |
|
|
|
k =∙│∙во |
втором |
слагаемом |
|||||||||||||||||||||||||||||||||||||||||||||||||
∂x ∂y ∂z |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
F ; F |
|
|
|
|
Fz ; Fx |
|
|
|
|
|
|
|
F ; F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Fx |
|
Fy |
|
Fz |
|
|
|
|
y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F |
∂Fy |
|
|
|
|
|
|
|
|
∂F |
|
∂F |
|
|
|
|
∂Fy |
|
∂F |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)i + ( |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
учтен знак минора |
|
|
│∙= ( |
|
|
|
z |
− |
|
|
|
|
|
|
x |
− |
|
|
|
z |
) j |
+ ( |
|
|
|
− |
x |
)k . |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂z |
|
∂x |
|
|
|
∂y |
|
|||||||||||||||||||||||||||||
|
|
Единичный |
|
|
нормальный |
|
|
|
|
вектор |
|
n к |
поверхности |
δ равен: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ cos(n,Oy) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ cos(n,Oz)k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
n = cos(n,Ox)i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Умножим левую и правую часть на ds: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
nds = cos(n,Ox)dsi |
|
+ cos(n,Oy)dsj |
|
+ cos(n,Oz)dsk |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
По формулам 3.16 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
dxdy = cos(n,Oz)ds , |
|
|
dydz = cos(n,Ox)ds , |
|
dxdz = cos(n, Oy)ds . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда вектор nds = dydzi + dxdzj + dxdyk .
Если осуществить скалярное произведение векторов:
|
|
|
|
|
|
|
|
|
|
∂F |
∂Fy |
|
|
|
|
|
∂F |
|
∂F |
|
|
|
|
∂Fy |
|
|
∂F |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
rotF |
nds =[ ( |
|
z |
− |
|
|
|
|
)i + ( |
|
x |
− |
z |
) j + ( |
|
|
− |
x |
)k ] |
|||||||||||||||||||
|
|
∂z |
∂z |
|
|
∂x |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
∂y |
||||||||||||
[ dydzi |
|
|
+ dxdzj |
|
+ dxdyk |
|
]= |
|
|
|
|
|
|
|
|
|
∂Fy |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= ( |
∂F |
|
|
|
∂Fy |
|
|
|
|
|
|
|
∂F |
|
|
|
|
∂F |
|
|
|
|
|
∂F |
|
)dxdy , то получим |
||||||||||||
|
|
z |
|
|
− |
|
)dydz + ( |
|
|
x |
|
− |
|
z |
)dxdz + ( |
|
|
|
− |
x |
||||||||||||||||||
∂y |
|
|
∂z |
|
|
|
|
|
∂x |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
∂x |
|
|
|
|
|
∂y |
|
|
|
|
|
|
||||||||||
подынтегральное выражение правой части развернутой формулы Стокса, а сама правая часть есть поток ротора вектора F через поверхность δ.
125
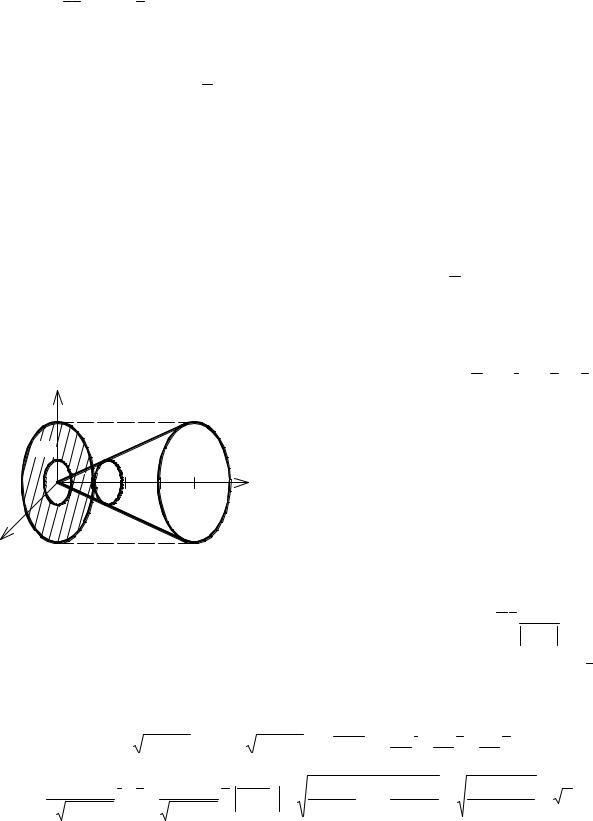
В сокращенном виде формула Стокса выглядит так:
Ц= ∫ Fdl = ∫∫rotFnds .
c δ
Циркуляция вектора F вдоль контура равна потоку ротора данного вектора через поверхность, натянутую на этот контур.
3.5.2.4. Типовые примеры решения поверхностных интегралов II рода
Пример 1. Вычислить поток векторного поля F через кривую поверхность тела V, заданного ограничивающими его поверхностями, нормаль внешняя.
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
F = 3xi −2 y j + zk , |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V : x2 + z2 = y2 , y =1, y = 4 . |
|
|
|
|
|||||||
σxz |
|
|
σ |
|
|
|
Решение. Кривая поверхность тела |
||||||||||
|
1 |
2 |
3 |
4 |
y |
V (рис. 3.33) есть боковая поверхность |
|||||||||||
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
усечённого конуса σ. Она однозначно |
|||||||||||
|
|
|
|
|
проектируется на плоскость y = 0 в виде |
||||||||||||
|
|
|
|
|
|
||||||||||||
|
Рис. 3.33 |
|
|
|
кольца. По формуле (3.19) определяем |
||||||||||||
|
|
|
|
расчётную формулу: |
П = ∫∫F n |
|
dxdz . |
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σxz |
cos β |
||
|
По формуле (3.11) определяем единичный нормальный вектор n |
||||||||||||||||
к поверхности σ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + z2 |
= y2 , y = |
x2 + z2 ,ϕ = y − |
x2 + z2 = 0, dradϕ = dϕ i + dϕ |
j + dϕ k = |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
dy |
dz |
|
|
|
|
= − |
2/ x |
i + j |
− |
z |
k, gradϕ = |
|
x2 |
+1+ |
|
z2 |
|
= |
2(x2 + z 2 ) |
= 2. |
|||
x2 + z2 |
+ z2 |
x2 |
+ z2 |
x2 |
+ z |
2 |
x2 + z2 |
|
|||||||||
2/ |
|
x2 |
|
|
|
|
|
|
|||||||||
126

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gradϕ |
|
|
x |
|
|
|
|
1 |
|
|
|
|
z |
|
|
|
|
|
||||
n = ± |
|
|
|
|
|
|
|
i + |
|
j + |
|
|
|
|
k |
|
|||||||
|
|
|
= ± |
− |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
ϕ |
|
2(x |
2 |
+ z |
2 |
) |
2 |
2(x |
2 |
+ z |
2 |
) |
||||||||||
|
|
||||||||||||||||||||||
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Выбираем знак «-» для вектора |
n |
|
. В формуле (3.19) для данного |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
случая стоит cosβ. В формуле (3.11) он имеет конкретное значение: cosβ= |
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
со знаком «+» . Но на рисунке 3.33 вектор |
|
|
и ось Oy составляют тупой угол, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
значит cos β |
|
отрицательный. Чтобы привести cosβ |
|
|
|
в формуле (3.11) в |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соответствие с рис.3.33, вектор |
|
|
нужно взять со знаком «-». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Окончательно: n = |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i − |
|
|
|
|
|
j + |
|
|
|
|
|
|
k. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(x2 + z 2 ) |
2 |
|
2(x2 + z2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Формируем расчётный интеграл. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
dxdz |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
П = ∫∫F ndS = ∫∫F n |
|
|
|
|
|
|
|
|
|
|
= ∫∫(3xi − |
2 y j + zk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
i − |
|
|
|
j + |
|
|
|
|
|
|
|
|
k |
|
|
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2/(x |
2 |
|
|
|
|
2 |
) |
|
|
|
2/(x |
2 |
|
|
2 |
) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
σ |
|
|
|
|
|
|
|
σxz |
|
|
|
|
cos β |
|
|
|
|
|
σxz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ z |
|
|
|
|
2/ |
|
|
|
|
|
|
|
|
+ z |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= σ∫∫xz |
|
|
|
+ 2 y + |
|
|
dxdz = |
|
σ∫∫xz |
|
|
|
|
+ 2 |
x |
|
+ z |
|
+ |
|
|
|
|
|
|
dxdz = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(x2 + z2 ) |
(x2 + z2 ) |
|
|
|
(x2 + z2 ) |
|
|
|
|
|
|
(x2 + z2 ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3x |
2 |
+ |
2(x |
2 |
+ z |
2 |
) + z |
2 |
|
|
|
|
|
5x |
2 |
|
+3z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= ∫∫ |
|
|
|
|
|
|
|
|
x |
2 |
+ z |
2 |
|
|
|
|
|
|
|
dxdz = ∫∫ |
|
|
|
|
x |
2 |
+ z |
2 |
dxdz = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
σxz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σxz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= ∙│∙ σ xz −есть кольцо: внутренняя окружность r1 = 1, внешняя окружность |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r2= 4. Перейдём к полярным координатам: x = rcosφ, z = rsinφ, 0≤φ≤2π, 1≤r≤4, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dxdy == rdrdφ ∙│∙ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 r 2 (2 cos2 ϕ + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2π |
|
|
|
4 5r 2 cos2 ϕ +3r 2 sin 2 ϕ |
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫ dϕ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rdr = ∫ dϕ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rdr |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
r 2 cos |
2 ϕ + r 2 sin 2 ϕ |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2π |
|
2 |
1 |
+ cos 2ϕ |
|
|
|
|
|
|
|
|
|
|
r3 |
|
4 |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
64 |
− |
1 |
= |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫ |
(2 cos2 ϕ + 3)dϕ∫r |
2 dr = ∫ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
+3 dϕ |
|
3 |
|
|
= ∫ |
(4 + cos 2ϕ)dϕ |
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
63 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
63 |
|
|
|
2π |
|
|
|
|
504 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
4ϕ |
+ |
|
sin 2ϕ |
|
|
|
|
|
= |
|
|
4ϕ |
|
|
|
|
|
|
= |
|
|
|
|
|
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 2. Даны векторное поле F и плоскость p, которая совместно с координатными плоскостями образует пирамиду V. Пусть σ – основание
127
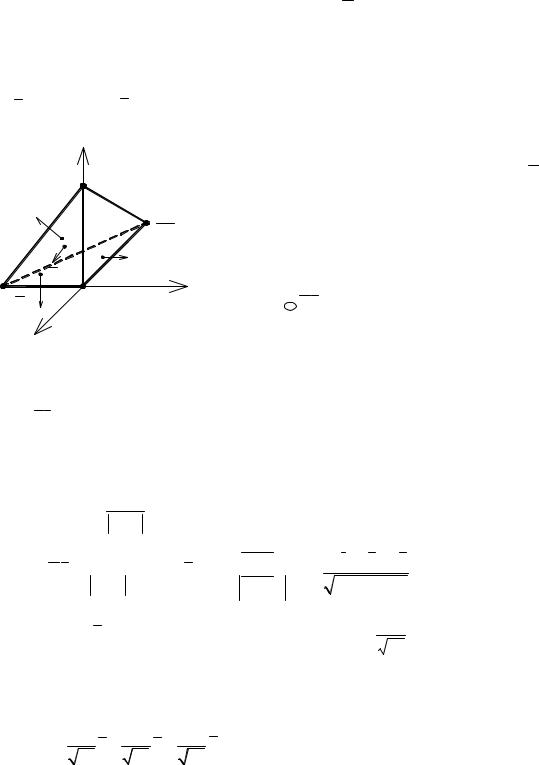
пирамиды, принадлежащее плоскости p, λ – контур ограничивающий σ. |
|||||||||||||||||
Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) поток векторного поля F через полную поверхность пирамиды |
||||||||||||||||
в направлении внешней нормали к её поверхности непосредственно; |
|
||||||||||||||||
|
б) тот же поток с использованием формулы Остроградского; |
||||||||||||||||
|
в) циркуляцию |
векторного |
поля |
F |
по замкнутому контуру λ |
||||||||||||
непосредственно; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
г) ту же циркуляцию – с использованием формулы Стокса. |
|
|||||||||||||||
F = (2z-3x-4y) j , p = 4z-3x-4y-4 = 0. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
z |
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|||
|
C 1 |
|
|
|
|
2а) Поток векторного |
поля |
F через |
|||||||||
nABC |
|
|
A |
4 |
полную поверхность пирамиды V (рис. 3.34), |
||||||||||||
|
|
|
- |
имеющей 4 грани равен сумме потоков через |
|||||||||||||
|
|
|
nAOC |
3 |
|||||||||||||
|
nBOC |
|
|
эти грани: |
|
|
|
|
|
|
|
|
|
|
|||
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
nAOB |
x |
|
|
|
y |
|
П = ∫∫F ndS = |
∫∫ |
|
+ ∫∫ + ∫∫ + ∫∫ |
|
||||||
|
|
|
|
|
|
|
σ |
|
DBC |
AOC |
AOB |
BOC |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ FnABC dS =∙│∙ поверхность |
АВС однозначно проектируется на все |
||||||||||||||||
ABC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координатные плоскости, поэтому можно выбрать любую из трёх формул |
|||||||||||||||||
(3.19). Пусть dS = cosdxdyγ |
∙│∙ = |
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫∫ |
F n ABC |
dxdy |
= |
∙ |
n ABC = ± |
grad p |
−3i −4 j + 4k |
|
|
|
|
||||||
cosγ |
│∙ |
grad p |
= ± |
2 |
|
2 |
+ 4 |
2 |
Выбираем знак «+» |
||||||||
AOB |
|
|
|
|
|
|
3 + 4 |
|
|
|
|
|
|
||||
в формуле для |
n ABC , так как в этом случае cosγ = |
4 |
|
> 0 |
в формуле и cosγ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- острый ). |
|
|||
также >0 в соответствии с рис.3. 34 ( угол γ = nABC Oz |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
4 |
∙ |
|
|
|
|
|
|
|
|
|
|
|
nABC = − 41 i − |
41 j + |
41 k |
│∙ = |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
128 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
dx4dy |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
= ∫∫ (2z −3x − 4 y)j |
− |
|
|
|
|
|
|
|
|
i − |
|
|
|
|
|
j + |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
= ∫∫ (2z −3x − |
|
4 y) − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
41 |
|
|
41 |
|
|
|
41 |
|
|
4 |
|
|
|
|
41 |
|
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΔΑΟΒ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= |
|
∫∫ |
(3x + 4 y −2z)dxdy = • |
|
• уравнение плоскости |
|
|
ABC : z = |
4 + 3x + 4 y |
• |
|
|
|
• = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ΔΑΟΒ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ΔΑΟΒ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
x + y |
|
|
|
|
|
|
|
|
|
|
ΔΑΟΒ∫∫ 2 |
|
x |
+ 2 y |
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3x + 4 y −2 |
1+ |
|
|
|
|
dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
• |
|
• AB : y = |
|
−3x −4 |
, AO : y = 0• |
|
• |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
3 |
x + 2 y −2 |
|
|
|
|
|
0 |
|
|
3 |
xy + y |
2 |
|
|
|
|
|
|
0 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ dx ∫ |
|
|
|
|
|
|
dy = ∫ dx |
|
|
|
|
|
|
−2 y |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
4 |
|
|
|
|
|
−3x−4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3x |
−4 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
3 |
|
|
|
|
|
|
|
|
|
−3x |
|
− |
4 |
|
|
|
|
|
|
|
|
|
−3x −4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3x −4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
= |
|
∫ |
|
|
|
x |
|
0 − |
|
|
|
|
|
|
|
|
|
|
|
+0 − |
|
|
|
|
|
|
|
|
|
− |
2 |
|
0 |
− |
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
−4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
9 |
|
|
2 |
|
|
|
|
3 |
|
|
|
9 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
9 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
9 x3 |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
x |
|
+ |
|
|
|
|
x − |
|
|
|
|
|
x |
|
|
− |
|
|
|
x −1− |
|
x −2 |
dx = |
|
|
|
|
|
|
|
|
x |
|
− |
|
|
|
x −3 |
dx = |
|
|
|
|
|
|
|
|
|
− |
|
|
|
x |
|
−3x |
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
8 |
|
2 |
16 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
2 |
16 3 |
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
−4∫/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4∫/ 3 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 / 3 |
||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
64 |
|
|
3 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
|
|
|
0 + |
|
|
|
|
|
|
− |
|
0 |
− |
|
|
|
|
−3 |
|
0 − |
|
|
|
= − |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
16 |
|
|
|
9 |
|
3 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
27 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
AOC dS = • |
|
|
|
AOC проектируется сам на себя, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
F |
|
|
n |
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dS = |
|
dxdz |
|
, n |
|
|
|
|
= |
|
|
|
, cos β =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙│ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos β |
|
|
|
|
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
= ∫∫ (2z −3x −4 y) |
|
|
|
jdxdz = ∫∫ (2z −3x −4 y)dxdz = • |
|
• y = 0, AC : z = |
4 +3x |
|
|
• |
= |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
• |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4+3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4+3x |
0 |
|
4 +3x |
|
2 |
|
|
|
|
|
4 +3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
(2z |
−3x)dz = |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫ |
|
|
dx |
|
∫ |
|
∫ |
dx |
z |
|
|
|
|
−3xz |
0 |
4 = |
|
∫ |
|
|
|
|
|
|
|
|
−3x |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−4 / 3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 / 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 / 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
27 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
9 |
|
|
|
|
|
3 |
|
|
0 |
|
4 |
|
|
|
3 |
|
|
16 |
9 43 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
|
|
x |
− |
|
|
|
|
|
x |
|
dx = x − |
|
|
|
|
|
x |
|
|
− |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
− |
|
|
|
− |
|
|
|
|
|
|
3 = |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
16 |
|
|
4 |
|
|
|
16 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−4∫/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 / 3 |
|
|
|
|
4 |
|
|
|
9 |
16 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
nAOB ds = • |
|
|
|
AOB проектируется сам на себя, |
|
AOB = − |
|
,cosγ = −1∙│∙ = |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
k |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫∫ F |
|
• |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫∫(2z − 3x − 4 y)j (− k )ds = 0
AOB
∫∫ |
|
|
|
BOC dS = • • |
|
BOC = |
|
• • = |
∫∫(2z − 3x − 4 y) |
|
|
|
dS = 0 |
F |
n |
n |
i |
j |
i |
||||||||
BOC |
BOC |
||||||||||||
129

|
|
|
П = ∫∫ |
|
nS = − |
20 |
+ |
|
4 |
|
= − |
|
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
3 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2б) по формуле Остроградского: П = ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
F |
nds = ∫∫∫divFdV. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divF |
|
= ∂Fx + |
∂Fy |
+ |
∂Fz |
|
= 0 + |
|
∂ |
|
(2z −3x −4 y) +O = −4. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
∂z |
|
|
∂y |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
1+ |
3 |
x+y |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
1+ |
3 |
x+y |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
П = ∫∫∫(−4)dv = −4∫∫∫dxdydz = −4 ∫ |
dx |
|
∫ |
|
|
dy |
|
|
|
∫ |
|
|
dz = −4 ∫ dx |
|
∫ |
dyz |
4 |
|
|
= |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ν |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
−4 |
3 |
|
|
|
− |
3 |
x−1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
− |
4 |
3 |
|
− |
3 |
x−1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||||||||
= −4 ∫0 |
dx ∫0 |
|
|
|
3 x + y)dy = −4 ∫0 |
|
|
|
|
|
|
|
4 |
|
|
3 xy + |
y2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
(1+ |
dx( y + |
) |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
−43 |
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
x−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
− |
x−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= −4 ∫0 |
(3 x +1+ 3 x( |
3 x +1) − |
1 |
(− |
3 x −1)2 )dx = −4 ∫0 |
( |
3 x +1+ |
9 |
|
|
x2 |
+ |
3 x − |
9 |
x2 − 3 x − |
1)dx = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
−4 3 |
4 |
|
|
|
|
4 4 |
|
|
|
|
2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 3 |
4 |
|
|
|
|
|
16 |
|
|
|
|
4 |
|
|
|
32 |
|
|
4 |
|
2 |
||||||||||||||||||||||||
0 |
|
1 |
|
3 |
|
|
9 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
3 |
|
16 |
|
3 |
|
64 |
|
8 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
−4 ∫ ( |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
+ |
|
|
|
x + |
|
|
|
x |
|
)dx = −4( |
|
|
x + |
|
|
|
x |
|
+ |
|
|
|
|
|
x |
) |
|
|
|
|
|
|
|
|
= −4 |
|
|
|
+ |
|
|
− |
|
|
|
+ |
|
|
|
= − |
|
|
. |
|||||||||||||||||||||||||
2 |
4 |
32 |
|
2 |
8 |
|
32 |
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
9 |
32 |
27 |
9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
−4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 3 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Ответы 2а и 2б совпали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2в) |
|
|
|
Циркуляция |
|
вектора |
|
|
|
|
|
|
|
|
|
|
вдоль |
контура-треугольника |
|
|
ABC |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(рис.3.34) непосредственно вычисляется:
Ц = ∫F dl = ∫F dl = ∫F dl + ∫F dl + ∫F dl.
l ABCA AB BC CA
∫ |
|
|
= |
|
|
• |
|
= (2z −3x − 4y) |
|
, |
|
= dxi |
|
+ dyj |
|
+ dzk |
|
• |
|
|
= |
F |
dl |
• |
|
F |
j |
dl |
|
|
|
|
• |
||||||||||
AB |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫(2z −3x −4 y)j (dxi + dyj + dzk )=
AB
= ∫(2z −3x − 4 y)dy=• |
|
• AB : 3x + 4 y + 4 = 0, z = 0• |
|
• = |
|||
|
|
||||||
AB |
|
|
|
|
|
|
|
= −∫14dy = 4 y |
|
−1 |
= −4. |
|
|
|
|
|
|
|
|
|
|||
0 |
|
0 |
|
|
|
|
|
130

∫ |
|
|
= ∫(2z −3x −4 y)dy=• |
|
•BC : z − y −1 = 0, x = 0• |
|
• = |
|
dl |
|
|
||||
F |
|||||||
BC |
|
|
BC |
|
|
|
|
= ∫0 (2( y +1) − 4 y)dy = ∫0 (2 − 2 y)dy =(2 y − y2 ) |
0 |
= −(−2 −1) = 3. |
||||||||
−1 |
|
|
−1 |
|
|
−1 |
|
|
|
|
∫ |
|
|
|
= ∫(2z −3x −4 y)dy=• |
|
•CA : 4x −3x −4 = 0, y = 0, dy = 0• |
|
• = 0 |
||
|
|
dl |
|
|
||||||
F |
||||||||||
CA |
|
|
CA |
|
|
|
|
|
|
|
Ц =  Fdl = −4 + 3 = −1.
Fdl = −4 + 3 = −1.
2г) По формуле Стокса: Ц = ∫l F dl = ∫∫rotFndS.
λσ
|
|
|
|
i |
|
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
∂ |
|
= − |
∂ |
(2z − 3x − 4 y) |
|
+ 0 |
|
+ |
∂ |
(2z − 3x − 4 y) |
|
= −2 |
|
− 3 |
|
. |
||||||
rotF |
|
= |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
i |
j |
k |
i |
k |
||||||||||||||||||||||
|
∂x |
|
∂y |
∂z |
∂z |
∂x |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
2z − 3x − 4 y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В формуле Стокса направление циркуляции вектора F и направление вектора n должны соответствовать правилу винта. В нашем случае вектор n должен быть по внешней нормали. Натянутая на контур λ поверхность есть плоский АВС.
|
|
Ц = ∫∫ |
|
|
|
|
nds = |
|
|
|
|
|
|
|
|
|
nABC ds = • |
|
|
• Воспользуемся случаем 2а: |
ds = |
|
dxdy |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
rotF |
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∫∫ rotF |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cosγ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
ABC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
dxdy |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
nABC |
= − |
|
|
|
|
i − |
|
|
|
|
j |
+ |
|
|
|
|
|
k• |
= |
∫∫ (−2i |
|
|
−3k ) |
− |
|
|
|
i − |
|
|
|
|
j + |
|
|
|
|
|
k |
|
4 |
|
|
= |
|
||||||||||||||||||||||||||||
41 |
|
41 |
41 |
41 |
41 |
|
|
41 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ∫∫ |
6 |
|
12 |
|
|
|
|
|
|
|
3 |
∫∫ |
dxdy = |
• |
|
• AB : y = − |
3 |
x |
−1, AO : y = 0• |
|
• |
|
|
|
3 |
|
|
0 |
dx |
0 |
|
dy = |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
− |
|
|
|
|
dxdy = − |
|
|
|
|
|
|
|
= − |
|
|
|
|
∫ |
∫ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
AOB 4 |
|
4 |
|
|
|
|
|
|
|
|
2 |
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
−4 3 |
− |
3 |
x |
−1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
0 |
|
|
|
|
|
|
3 0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
2 |
|
|
|
|
|
0 |
|
|
|
3 3 |
|
|
|
|
16 |
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= − |
|
|
dxy |
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
x +1 dx = − |
|
|
|
|
|
|
|
x |
|
+ x |
|
|
= − |
|
|
|
− |
|
|
|
+ |
|
|
|
|
= −1. |
|
|
|
|||||||||||||||||||||||||
2 −∫4 3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
− |
x−1 |
|
|
2 −∫4 3 4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
8 |
|
|
|
|
|
|
|
|
−4 3 |
|
|
|
2 8 |
|
|
|
|
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответы 2в и 2г совпали.
131

z |
|
|
Пример 3. Поверхность тела образована |
|||||||
1 C |
|
|
цилиндрическим параболоидом P и координатными |
|||||||
|
|
|
плоскостями. Найти: |
|
|
|
|
|||
0 |
|
B |
а) |
циркуляцию |
вектора |
F |
вдоль |
контура, |
||
|
1 |
y |
||||||||
A |
|
образованного |
|
пересечением |
|
цилиндрического |
||||
|
|
|
|
|||||||
x1 |
|
|
параболоида |
с |
координатными |
плоскостями |
||||
Рис. 3.35 |
|
|||||||||
|
непосредственно; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
б) ту же циркуляцию – с помощью формулы Стокса; |
|
|
||||||||
в) |
поток векторного |
поля |
F |
через |
полную |
поверхность |
тела в |
|||
направлении внешней нормали непосредственно; г) тот же поток с помощью формулы Остроградского.
F = (5x + y 2 − 2z)i + (x −3y − z 2 )j + (x2 + 2 y − z)k .
p : y 2 =1 − x − z.
Решение. а) Непосредственным образом циркуляция вектора F по полученному контуру (рис.3.35) равна:
Ц = ∫Fdl = ∫Fdl = ∫Fdl + ∫Fdl + ∫Fdl .
|
ABCA |
AB |
BC |
CA |
|||||||||
∫ |
Fdl = ∫[(5x + y 2 |
− 2z)i |
+ (x − 3y − z 2 ) |
|
+ (x2 + 2 y − z)k |
](dxi |
|
+ dyj |
|
+ dzk |
|
)= |
|
|
|
||||||||||||
j |
|
|
|||||||||||
AB |
AB |
|
|
|
|
|
|
|
|
|
|
|
|
∫(5x + y 2 − 2z)dx + (x − 3y − z 2 )dy + (x2 + 2 y − z)dz =
AB
132

=• |
|
|
• z = 0, dz = 0, AB : x =1 − y 2 , dx = −2 ydy • |
|
|
|
• |
|
= ∫1 [5(1 − y 2 )+ y 2 ](− 2 y)dy + (1 − y 2 |
− 3y)dy = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||
= ∫ |
(−10 y + |
8y |
|
+1 − y |
|
− 3y)dy =∫(1 −13y − y |
|
|
|
+ 8y |
|
)dy |
= y − |
|
|
|
y |
|
− |
|
|
|
|
|
y |
|
|
+ 2 y |
|
|
|
|
|
|
|
= |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||
=1 − |
13 |
− |
1 |
|
+ 2 |
= − |
23 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫ |
|
|
|
|
|
|
|
(5x + y 2 − 2z)dx + (x − 3y − z 2 )dy + |
|
|
|
(x2 |
|
+ 2 y − z)dz = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Fdl = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
BC |
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫1 [− 3y − (1 − y 2 )2 ]dy + (2 y −1 + y 2 )(− 2 y)dy = |
||||||||||||||||||||||||||||||||||||||||||||||||||||
=• |
|
|
• x = 0, dx = 0, BC : z =1 − y 2 , dz = −2 ydy • |
|
|
|
• |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫1 [− 3y −1 + 2 y 2 − y 4 − 4 y 2 + 2 y − 2 y3 ]dy = ∫1 (−1 − y − 2 y 2 − 2 y3 − y 4 )dy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
4 |
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
3 |
|
|
1 |
|
|
4 |
|
1 |
|
|
5 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
1 |
|
|
|
43 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= ∫ |
(1 + y + 2 y |
|
|
+ 2 y |
|
+ y |
|
)dy = y + |
|
y |
|
+ |
|
|
|
|
y |
|
|
+ |
|
y |
|
+ |
|
|
|
y |
|
|
|
=1 + |
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
+ |
|
|
|
|
|
= |
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
3 |
|
|
|
|
|
2 |
|
5 |
|
|
|
2 |
|
3 |
|
2 |
|
5 |
|
15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫ |
|
|
= ∫(5x + y 2 |
− 2z)dx + (x − 3y − z 2 )dy + (x2 |
+ 2 y − z)dz = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Fdl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
=• |
|
|
• y = 0, dy = 0, CA : z =1 − x, dz = −dx • |
|
• = ∫1 [5x − 2(1 − x)]dx + (x2 −1 + x)(− dx)= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= ∫ |
(7x − 2 − x |
|
|
+1 |
− x)dx = ∫(−1 + x − x |
|
|
)dx = |
− x + |
3x |
|
|
− |
|
|
|
x |
|
|
|
|
= −1 + 3 − |
|
|
|
|
= |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Ц = ∫Fdl = − 236 + 1543 + 53 = 3021 .
б) По формуле Стокса циркуляция вектора равна:
Ц = ∫Fdl = ∫∫rotFndS.
σ
Поверхность σ однозначно проектируется на все три координатные плоскости, поэтому можно для расчета вектора выбрать любую из трех формул (3.19). При этом расчет потока вектора будет значительно проще, если проектировать σ на плоскости z = 0 или x = 0 и этот расчет усложняется, если проектировать σ на плоскость y = 0.
Пусть поверхность σ спроектирована на плоскость x = 0. Тогда:
Ц = ∫ |
|
|
|
|
|
|
|
|
|
|
dydz |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
Fdl = ∫∫rotFndS = ∫∫rotFn |
|
|||||||||||||||
|
|
cosα |
|
|
||||||||||||
|
|
|||||||||||||||
|
|
|
|
σ |
|
σ yz |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
133

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
j |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
∂ |
|
|
|
|
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
rotF = |
|
|
|
|
|
|
|
|
|
= (2 |
+ 2z)i − (2 |
+ 2x)j + (1 − 2 y)k . |
|||||||||||||||||||||||||
|
∂x |
|
|
|
∂y |
|
|
|
|
∂z |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
5x + y 2 − 2z x − 3y − z 2 x2 + 2 y − z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Поверхность σ |
- это |
поверхность цилиндра |
y 2 =1 − x − z. Найдем |
||||||||||||||||||||||||||||||||||
единичный нормальный вектор к этой поверхности. |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
grad |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ϕ = x + y 2 + z −1, n = ± |
|
= ± |
i |
+ 2 yj + k |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
grad |
|
|
|
2 + 4 y 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
Циркуляция вектора |
|
|
происходит по контуру ABCA (рис.3.35), на |
||||||||||||||||||||||||||||||||||
F |
|||||||||||||||||||||||||||||||||||||
который натянута поверхность σ . Направление циркуляции вектора F по правилу винта связано с направлением вектора n к поверхности σ . В данном случае это внешняя нормаль, которая составляет острые углы со всеми координатными осями. Направляющие косинусы положительные. В формуле для n все направляющие косинусы также положительные. Значит знак единичного нормального вектора n должен быть «+».
|
|
|
|
|
|
|
|
|
|
|
dydz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i + 2 y |
j |
+ |
|
k |
|
|
|
|
|
dydz |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫∫[(2 + 2z)i − (2 + 2x)j + (1 − 2 y)k] |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Ц = ∫∫rotFn |
= |
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
cosα |
|
|
2 + |
4 y |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
σ yz |
|
|
|
|
|
|
|
|
|
|
BJC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + 4 y2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= ∫∫(2 + 2z − 4 y − 4xy +1 − 2 y)dydz=• |
|
•σ : x =1 − z − y 2 , BC : z =1 − y2 |
• |
|
|
• |
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
BOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1−y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1−y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= ∫dy ∫ |
[3 + 2z − 6 y − 4 y(1 − z − y2 )]dz =∫dy |
|
∫(3 + 2z −10 y + 4 yz + 4 y3 )dz = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= ∫1 dy[(3 −10 y + 4 y3 )z + z 2 + 2 yz 2 ] |
1−y2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫1 [(3 −10 y +10 y3 )(1 − y 2 )+1 − 2 y2 + y4 + 2 y − 4 y3 + 2 y5 ]dy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫1 (3 −10 y + 4 y3 −3y 2 +10 y3 − 4 y5 +1 − 2 y 2 + y 4 + 2 y − 4 y3 + 2 y5 )dy = |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
4 |
|
5 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
||||||||||||
= ∫(4 −8y −5y |
|
+10 y |
|
+ y |
|
|
− 2 y |
|
)dy = 4 y |
− 4 y |
|
− |
|
y |
|
+ |
|
y |
|
+ |
|
|
|
|
y |
|
− |
|
|
|
|
y |
|
|
|
= |
|||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
2 |
|
5 |
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||
= 4 − |
4 − |
5 |
+ |
5 |
|
+ |
|
1 |
− |
|
1 |
= |
21 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
5 |
3 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Как и следовало ожидать, результаты совпали.
134
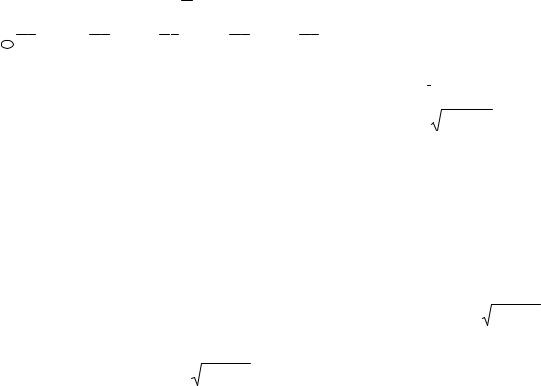
в) Поток векторного поля F через полную поверхность тела:
П = ∫∫F ndS = ∫∫ F ndS + ∫∫F ndS + ∫∫ F ndS + ∫∫F ndS.
|
|
σ |
ABC |
|
AOB |
BOC |
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
i + 2 y |
|
+ |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
grad |
|
|
j |
k |
||||||
∫∫FnABC dS. |
p : y |
=1− x − z,ϕ = x + y |
+ z −1, nABC = ± |
|
|
|
|
= ± |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||
|
|
|
gradϕ |
2 + 4 y |
||||||||||||||||||
ABC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выбираем перед формулой для nABC знак «+», т.к. вектор nABC с
любой координатной осью составляет острый угол, а значит, любой направляющий косинус – положительный. Поверхность АВС однозначно проектируется на любую координатную плоскость. Поэтому можно выбрать
любую из трёх расчётных формул (3.19). Но формула для |
cos β = |
|
2 y |
|
||||
|
+ 4 y2 |
|||||||
|
|
|
|
|
2 |
|||
сложнее, чем для cosα = cosγ = |
|
1 |
, |
что в дальнейшем приведёт к |
||||
|
+ 4 y2 |
|||||||
2 |
|
|
|
|
|
|
||
«осложнениям» в расчёте потока вектора. Выбираем проекцию поверхности АВС на плоскость z = 0 и это будет плоская область АОВ.
135
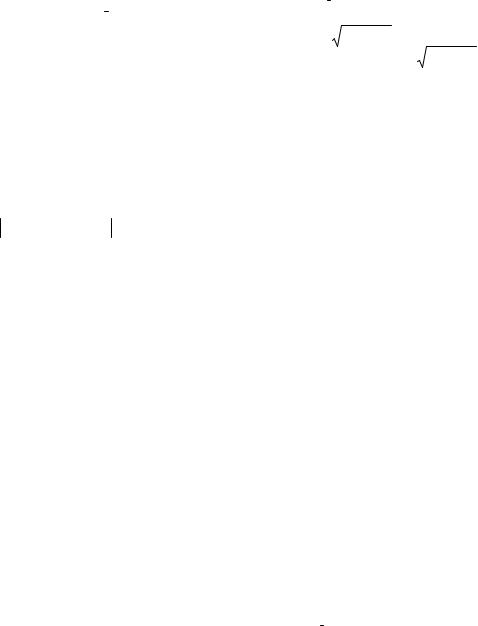
∫∫ |
|
nABC dS = ∫∫ |
|
nABC |
|
|
dxdy |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ABC |
|
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i + 2y |
|
+ |
|
|
|
|
|
dxdy |
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
j |
k |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫[(5x + y − 2z)i + (x − 3y − z )j + (x + 2y − z)k] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||
2 + 4y |
2 |
|
|
1 |
|
|
|
|||||||||||||||||||||||||||
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + 4y2 |
||||||||||||||
= ∫∫(5x + y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
+ 2y − z)dxdy=• |
|
|
|
|
|
|
|
|
|
|
|||||||||||
− 2z + 2xy − 6y2 |
− 2yz2 |
+ x2 |
|
|
• z =1 − x − y2 |
• |
|
• = |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= AOB∫∫[5x + 2y − 5y2 + 2xy −3(1 − x − y 2 )− 2y(1 − x − y2 )2 + x2 ]dxdy = |
|
|
|
|
|
|||||||||||||||||||||||||||||
=AOB∫∫(5x + 2y − 5y2 + x2 + 2xy − 3 + 3x + 3y2 − 2y − 2yx2 − 2y5 + 4xy + 4y3 − 4xy3 )dxdy =
AOB
11−y2
•AB : x =1 − y2 • • = ∫dy ∫(− 3 + 8x + x2 − 2y 2 + 6xy − 2yx2 + 4y3 − 4xy3 − 2y5 )dx =
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
5 |
|
1−y2 |
|
|
2 |
|
|
|
1 |
|
|
3 |
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= ∫dy (−3 − 2y |
|
+ |
4y |
|
− |
2y |
|
)x |
|
+ |
4x |
|
+ |
|
|
x |
|
+ |
3x |
|
y − |
|
|
|
||||||||||||||
|
|
|
|
|
3 |
|
|
3 |
|
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
(− 3 − 2y 2 |
+ 4y3 − 2y5 )(1 − y2 )+ 4(1 − y2 )2 + |
(1 − y2 )3 |
+ |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
= ∫ |
|
3 |
(1 − y |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
− 2y |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
−3 − 2y |
2 |
+ 4y |
3 |
− 2y |
5 |
+ 3y |
2 |
+ 2y |
4 |
− 4y |
5 |
+ 2y |
7 |
+ 4 −8y |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= ∫ |
|
|
|
|
3 + 3y5 − |
|
2 |
y + 2y3 − 2y5 |
|
|
2 |
y7 − 2y3 + 4y5 |
|
|
|
|||||||||||||||||||||||
0 + 3y − 6y |
|
+ |
|
− |
||||||||||||||||||||||||||||||||||
3 |
|
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yx |
3 |
− 2x |
2 |
y |
3 |
|
|
1−y2 |
|
= |
|
|
|
||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3y(1 − y2 )2 − |
|
|
y(1 − y2 )3 |
− |
|||||||||||||
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy = |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 4y4 + |
1 |
|
− y2 + y 4 − |
1 |
y6 + |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
3 |
dy = |
|||||
2y7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= ∫ |
|
|
|
|
+ |
|
|
|
|
|
y |
− |
|
8y |
|
|
− |
2y |
|
|
+ 7 y |
|
|
|
|
− y |
|
|
− |
|
|
|
|
y |
|
+ |
|
|
|
|
|
|
y |
|
dy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
4 |
|
|
y + |
7 |
|
y |
2 |
|
|
|
− |
|
8 |
|
y |
3 |
− |
1 |
|
y |
4 |
+ |
7 |
|
y |
5 |
− |
|
1 |
|
|
y |
6 |
|
− |
|
|
1 |
|
|
|
y |
7 |
+ |
1 |
y |
8 |
|
|
1 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
3 |
|
|
6 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
5 |
|
|
|
6 |
|
|
|
|
|
21 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= |
|
4 |
+ |
|
7 |
− |
|
8 |
− |
|
1 |
|
+ |
|
7 |
|
− |
1 |
− |
1 |
|
|
+ |
|
|
1 |
|
= |
|
253 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
3 |
|
6 |
3 |
|
2 |
|
5 |
|
6 |
21 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
420 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
](− |
|
|
||||||||||||||||||||||||||||||||
∫∫ |
|
|
nAOBdS=• |
|
• nAOB = − |
|
|
, z =0 • |
|
|
• |
|
= ∫∫[(5x + y2 |
− 2z)i + (x −3y − z 2 ) |
|
+ (x2 |
+ 2y − z) |
|
|
)dxdy = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F |
k |
|
j |
k |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1−y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1−y2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= ∫∫(− x |
|
|
|
|
− 2y)dxdy= |
|
|
|
|
• AB: x =1 − y |
|
• |
|
|
|
= ∫dy ∫(− x |
|
− 2y)dx =∫dy |
− |
|
|
x |
|
− 2yx |
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
AOB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= ∫ |
− |
|
(1 |
− y |
|
|
) |
|
2y(1 − y |
|
|
)dy = ∫ |
− |
|
|
|
(1 |
−3y |
|
|
|
+3y |
|
− y |
|
)− 2y + 2y |
|
dy = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
5 |
|
|
|
|
7 |
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|||||||||||||||||||||||
= ∫ |
− |
|
+ y |
|
|
− y |
|
|
|
+ |
|
|
|
y |
|
|
− 2y + 2y |
|
dy = |
|
− |
|
|
|
|
|
y + |
|
|
y |
|
− |
|
|
|
y |
|
+ |
|
|
y |
|
− y |
|
+ |
|
y |
|
|
= |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
3 |
|
|
|
|
3 |
3 |
|
|
5 |
|
21 |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||||||||||||||
= − |
|
1 |
|
+ |
1 |
|
− |
|
1 |
+ |
1 |
|
|
−1 + |
1 |
|
= − |
137 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
3 |
3 |
|
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
210 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
136

∫∫ |
|
|
nBOC dS =• |
|
• nBOC |
|
= −i, x = 0 • |
|
|
|
• = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
BOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫∫[(5x + y 2 −2z)i +(x −3y − z 2 ) |
|
+(x 2 + 2 y − z) |
|
](−i)dydz = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
j |
k |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
BOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1−y2 |
1 |
|
|
|
1−y |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= ∫∫(2z − y 2 )dydz=• |
|
• BC : z =1− y 2 |
• |
|
|
• |
= ∫dy |
∫(2z − y 2 )dz =∫dy(z 2 − y 2 z) |
= |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
BOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
||||
= ∫1 [(1− y 2 )2 − y 2 (1− y 2 )]dy = ∫1 (1−2 y 2 + y 4 − y 2 + y 4 )dy = ∫1 (1−3y 3 + 2 y 4 )dy = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
2 |
|
|
|
5 |
|
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= y − y |
|
+ |
|
|
y |
|
|
|
=1−1+ |
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
5 |
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫∫ |
|
nAOC dS=• |
|
• nAOC = − |
|
, y = 0 • |
|
|
• |
|
|
= ∫∫[(5x + y2 − 2z)i + (x − 3y − z 2 ) |
|
+ (x2 |
+ 2y − z) |
|
](− |
|
)dxdz = |
|||||||||||||||||||||||||||
F |
|
j |
|
|
j |
k |
j |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
1 |
|
|
|
1−x |
|
|
2 |
|
|
|
|
|
1 |
|
1 |
|
|
3 |
|
1−x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= ∫∫(z |
|
− x)dxdz= |
|
|
|
• AC |
: z =1 |
− x • |
|
|
= ∫dx ∫ |
(z |
|
− x)dz =∫dx |
|
|
z |
|
− xz |
= |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
AOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
||||||
|
1 |
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
2 |
|
|
|
1 |
|
|
3 |
|
|
|
|
2 |
|
|
1 |
|
1 |
|
|
2 |
|
|||||||
= ∫ |
|
(1 |
− x) |
|
− x(1 − x) dx = ∫ |
|
|
|
|
− x |
+ x |
|
|
− |
|
|
|
x |
|
|
− x + x |
|
dx = ∫ |
|
− 2x |
+ 2x |
|
− |
||||||||||||||||||||||||||||
3 |
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||
|
1 |
x − x |
2 |
|
|
2 |
x |
3 |
|
|
|
1 |
y |
4 |
|
1 |
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= |
|
|
|
+ |
|
|
− |
|
|
|
|
= |
|
|
|
|
−1 |
+ |
|
|
− |
|
|
|
|
|
= − |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
3 |
|
12 |
3 |
3 |
|
12 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
П = 420253 − 137210 + 52 −121 = 112420 = 154 .
г) Определим тот же поток по формуле Остроградского:
div |
|
= |
∂ |
(5x + y2 − |
2z)+ |
∂ |
(x −3y − z2 )+ |
|
∂ |
|
|
(x2 + 2 y − z)= 5 −3 −1 =1. |
|||||
F |
|
|
|||||||||||||||
∂x |
∂y |
|
∂z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
1− y 2 |
1−x− y 2 |
1 |
1− y 2 |
|
1−x− y |
2 |
1 |
1− y 2 |
||||
|
|
|
|
|
|||||||||||||
П = ∫∫∫dV = ∫dy ∫dx ∫dz = ∫dy ∫dxz |
|
|
|
= ∫dy ∫(1 − x − y2 )dx = |
|||||||||||||
|
|
V |
|
0 |
0 |
0 |
|
0 |
0 |
|
|
0 |
|
|
0 |
0 |
|
13 x3 dx =
П = ∫∫∫divFdV.
V
|
1 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
1− y 2 |
1 |
|
|
|
|
2 |
|
1 |
|
|
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= ∫dy x − |
|
|
|
x |
|
|
− y |
|
x |
|
|
|
|
|
= ∫ |
1 |
− y |
|
− |
|
(1 |
− y |
|
) − y |
|
(1 |
− y |
|
) dy = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
1 |
|
|
4 |
|
2 |
|
|
4 |
|
|
|
1 |
1 |
|
|
2 |
|
1 |
|
|
4 |
|
|
|
1 |
|
|
1 |
|
3 |
|
1 |
|
5 |
|
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= ∫ 1 |
− y |
|
|
|
− |
|
|
+ y |
|
− |
|
|
|
|
y |
|
− y |
|
+ y |
|
dy |
= ∫ |
|
|
|
− y |
|
+ |
|
|
y |
|
dy = |
|
|
y − |
|
y |
|
+ |
|
|
y |
|
|
|
= |
|||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
3 |
|
10 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||
= |
1 |
− |
|
1 |
+ |
|
|
1 |
|
= |
|
8 |
|
= |
|
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
3 |
10 |
|
|
30 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответы потоков через полную поверхность совпали.
137
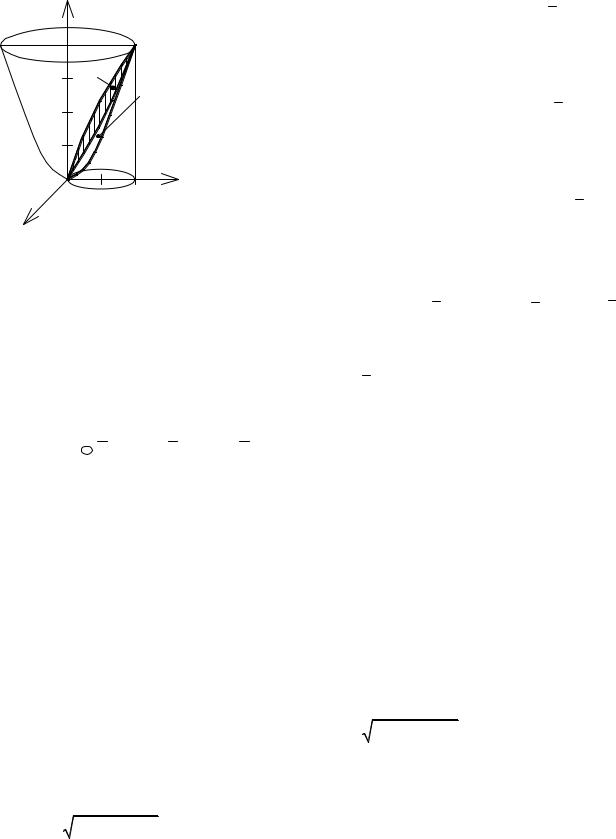
z |
|
|
|
|
Пример 4. Даны векторное поле F |
и |
две |
||||||||
|
|
|
|
|
|||||||||||
4 |
|
|
|
поверхности, |
образующие |
пространственное |
|
тело |
|||||||
3 |
z = 2y |
|
|
ограниченное |
|
замкнутой |
поверхностью |
|
σ . |
||||||
|
z = x2+ y2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
Вычислить: а) поток векторного поля |
F |
через |
|||||||||
1 |
V |
|
|
полную поверхность σ |
тела (нормаль внешняя); б) |
||||||||||
|
1D |
2 |
y |
тот |
же |
поток |
– |
с |
использованием |
формулы |
|||||
x |
|
|
|
Остроградского; |
в) |
циркуляцию |
вектора |
F |
по |
||||||
|
|
|
замкнутому |
контуруγ , |
образованного |
|
при |
||||||||
|
Рис. 3.36 |
|
|
||||||||||||
|
|
пересечении данных поверхностей; г) ту же |
|||||||||||||
|
|
|
|
||||||||||||
циркуляцию – с использованием формулы Стокса |
F = (3x − y − z)i + 3yj + 2zk , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
% |
|
|
σ1 : z = x2 + y2 ,σ2 : z = 2 y. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
4а) Поток векторного поля F |
через полную поверхность σ |
|||||||||||||
равен сумме потоков через обе поверхности: |
|
|
|
|
|
|
|
||||||||
П = ∫∫FndS = ∫∫Fn1dS + ∫∫Fn2 dS,
σ |
σ1 |
σ2 |
где σ1 - поверхность z = x2 + y2, или ϕ1 = x2 + y2 − z = 0 - параболоид вращения ,
σ2 - поверхность z = 2y, или ϕ2 = 2 y − z = 0 - плоскость (рис. 3.36). Обе поверхности однозначно проектируются на плоскость z = 0. Поэтому оба
потока через σ1 и σ2 |
вычислим по одной и той же формуле (3.19), у которой |
||||||||||||||||||||||||||||||||||||||
ds = |
dxdy |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
• |
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2xi |
+ 2 yj |
− k |
. Для |
|
выбираем |
|||||||||||||||
|
∫∫Fn1ds = ∫∫ |
Fn1 |
|
|
= |
• n1 |
= ± |
|
= ± |
n1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
cosγ |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
gradϕ1 |
4x |
+ 4 y |
+1 |
||||||||||||||||||||||||||||||||
|
σ1 |
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
знак |
«+». |
|
|
|
|
|
|
|
Это |
|
|
приводит |
|
в |
|
|
|
соответствие |
знак |
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosγ = − |
|
|
|
|
|
|
|
|
|
|
< 0 ,определяемого по формуле для n , со знаком того |
||||||||||||||||||||||||||||
|
+ 4 y2 |
+1 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
4x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
жеcos γ < 0 , |
определяемого |
по |
рис.3.36. |
На |
рис.3.36 |
видно, |
что по всей |
||||||||||||||||||||||||||||||||
поверхности |
|
σ |
1 |
|
|
угол |
( n ^ Oz) = γ -тупой, |
|
а |
|
значит |
|
cos γ < 0 |
• |
|
• = |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
138

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2xi |
+ 2 yj |
− k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= ∫∫ (3x − y − z)i + 3yj + 2zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
+ 4 y |
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
− z)2x + 6y |
2 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− 2xy − 2xz + 6y |
2 |
− 2z)dxdy = |
• |
|
• z = x |
2 |
|
|
2 |
|
• |
= |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
= ∫∫ (3x − y |
|
2z dxdy = ∫∫(6x |
|
|
|
|
|
|
+ y • |
|
|
||||||||||||||||||||||||||||||||||||||||||||
σчн |
|
− 2xy − 2x(x |
|
+ y |
|
) + 6 y |
|
|
|
|
σxy |
|
+ y |
|
))dxdy = |
∫∫ 4(x |
|
|
+ y |
|
) − 2xy − |
2x(x |
|
+ y |
|
) dxdy = |
|||||||||||||||||||||||||||||
= ∫∫(6x |
|
|
|
|
− 2(x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
пересечении |
|
поверхностей |
|
и |
|
|
|
|
образуется |
|
кривая – |
|||||||||||||||||||||||||||||||||||||||||||
|
σ1 |
σ 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
пространственный эллипс (рис.3.36), проекция которой на плоскость z=0 есть
окружность. Это значит, что обе поверхности σ1 и σ 2 имеют одну и ту же проекцию σ xy в виде круга.
Выведем уравнение этой окружности:
z = x2 + y 2 , z = 2 y, x2 + y 2 = 2 y, x2 + (y −1)2 =1
Это уравнение окружности, смещенной вправо на 1, с радиусом
равным 1. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Для |
вычисления |
потока поля |
|
|
перейдем к полярной |
системе |
|||||
F |
|||||||||||||||
координат. Уравнение окружности примет вид: |
|
||||||||||||||
|
|
|
|
x = r cosϕ, y = r sinϕ, r 2 cos2 ϕ + (r sinϕ −1)2 |
=1, r 2 cos2 ϕ + r 2 sin 2 ϕ − 2r sinϕ +1 =1, |
||||||||||
|
|
|
|
r 2 |
= 2r sinϕ, r = 2sinϕ,0 ≤ π. |
|
|
|
|
||||||
|
|
|
|
Вернемся к вычислению потока вектора |
|
через поверхность σ1 : |
|||||||||
F |
|||||||||||||||
∫∫ |
|
|
|
|
|
= r2 , r = 2sinϕ, |
|||||||||
F |
ndS = ∫∫ 4(x2 + y2 )−2xy −2x (x2 + y2 ) dxdy = •• x = r cosϕ, y = r sinϕ, x2 + y2 |
||||||||||||||
σ1 |
σxy |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
π |
2sinϕ |
|
|
|
|
||
0 ≤ϕ ≤π, dxdy = rdrdϕ• |
|
• = ∫dϕ ∫ (4r2 −2r2 cosϕ sinϕ −2r3 cosϕ)rdr = |
|
||||||||||||
|
|
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
2 sin ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫dϕ |
∫ (4r3 − 2r3 cosϕsinϕ − 2r4 cosϕ)dr = |
|
|||||||||
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
139

|
π |
|
|
|
(r |
4 |
− |
1 |
r |
4 |
cosϕ sinϕ |
− |
2 |
r |
5 |
cosϕ) |
2 sin ϕ |
= |
|
π |
|
|
|
|
|
|
|
|
|
|
4 |
|
ϕ −8cosϕsin |
5 |
|
ϕ |
|
− |
|
64 |
cosϕsin |
5 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫dϕ |
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
∫ |
16sin |
|
|
|
|
|
|
|
5 |
|
|
ϕ dϕ = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
π |
|
|
|
1 |
− cos 2ϕ 2 |
dϕ − |
104 |
π |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
(1 − 2 cos 2ϕ + cos |
2 |
2ϕ)dϕ − |
104 |
|
sin6 ϕ |
|
π |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫16 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
5 |
∫sin |
|
|
ϕd sinϕ = ∫4 |
|
|
|
|
|
5 |
|
6 |
|
|
|
|
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ cos 4ϕ |
|
|
|
|
|
|
|
|
π |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
π |
||||||||||||||||||||
= 4 |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
4 |
|
− 2 cos 2ϕ + |
cos 4ϕ |
|
|
|
|
|
|
|
|
|
|
ϕ −sin 2ϕ + |
sin 4ϕ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 − 2 cos 2ϕ |
|
|
|
|
|
|
|
|
dϕ = |
∫0 |
|
|
|
|
|
|
dϕ = 4 |
|
|
|
|
|
|
|
|
= 6π. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
∫∫Fn2 ds = ∫∫Fn2 |
|
= |
|
|
|
n2 |
|
= ± |
2 |
|
= ± |
|
|
|
|
|
= ± |
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
+1 |
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
gradϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
σ2 |
|
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для n2 выбираем знак «-» На рис.3.36 единичная нормаль n2 к поверхности |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
σ2 (плоскости) всюду имеет острый угол |
|
γ =( n2 ^Oz), |
|
|
а значитcosγ > 0 . В |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
формуле для |
|
|
n |
|
cosγ = − |
1 |
|
< 0 . Чтобы устранить это несоответствие, |
знак n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
выбираем «-» тогда n |
|
= − |
2 |
|
|
+ |
|
|
1 |
|
|
|
|
|
|
• |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
• |
|
|
||||||||||||||||||||||
∫∫ (3x − y − z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫(−6 y + 2z)dxdy = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
i |
+ 3yj |
+ 2zk |
− |
|
|
|
|
|
j + |
|
|
|
|
|
|
k |
|
|
|
|
1 |
|
|
|
|
|
|
= |
|
•σ2 : z |
= 2 y • |
|
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
σ |
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= ∫∫(−6y + 4 y)dxdy = ∫∫(−2 y)dxdy = • |
|
|
• |
|
|
Перейдем к полярным координатам. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Область интегрирования σxy - |
|
тот же круг: r = |
2sinϕ , |
|
|
|
|
0 ≤ ϕ ≤ π , y |
= rsinϕ , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dxdy = rdrdϕ • |
|
• |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
π |
|
|
|
2 sin ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
2sinϕ |
|
|
|
|
2 |
|
π |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
π |
|
|
1 − сos2ϕ |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
= −2∫dϕ |
∫ |
|
r sinϕrdr = −2∫sinϕdϕ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
∫8sin |
|
ϕdϕ |
= − |
|
|
|
|
|
|
∫ |
8 |
|
|
|
|
|
|
|
|
|
|
|
dϕ = |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
− 2 π∫2(1 − 2сos2ϕ + + cos2 2ϕ)dϕ = − |
|
2 π∫(2 − 4 cos 2ϕ + |
1 + cos 4ϕ)dϕ = − |
2 π∫(3 − 4 cos 2ϕ + cos 4ϕ)dϕ = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= − |
2 (3ϕ |
− 2sin 2ϕ + 1 sin 4ϕ) |
|
π |
|
= −2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П = ∫∫ |
|
ndS = 6π − 2π = 4π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4б) По формуле Остроградского: П = ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
F |
ndS = ∫∫∫divFdV. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
140

div F = ∂∂x (3x − y − z) + ∂∂y 3y + ∂∂z 2z = 3 + 3 + 2 = 8.
П = ∫∫∫8dV = 8V
V |
|
|
|
|
Вычисление объема |
V |
произведем |
в цилиндрической системе |
|
координат. Область V |
(рис.3.36) снизу |
ограничена |
поверхностью |
|
z = x2 + y2 = r 2 cos2 ϕ + r 2 sin 2 ϕ = r 2 |
(нижний |
предел |
интегрирования |
|
внутреннего интеграла), сверху - плоскостью z = 2 y = 2r sin ϕ |
(верхний предел |
|||
интегрирования), область D –область интегрирования двойного интеграла –
круг - r = 2 sin ϕ,0 ≤ ϕ ≤ π.
|
|
π |
2 sin ϕ |
2r sin ϕ |
π |
2 sin ϕ |
|
π |
V = ∫∫∫dV = ∫∫∫rdrdϕdz = ∫dϕ |
∫ rdr |
∫dz =∫dϕ |
∫ |
rdr z |
r22r sin ϕ = ∫dϕ |
|||
V |
V |
0 |
0 |
r 2 |
0 |
0 |
|
0 |
2 sin ϕ
∫r(2r sinϕ − r 2 )dr =
0
|
π |
|
|
2 sin ϕ |
2 |
|
|
|
|
|
|
3 |
π |
|
|
|
|
|
r 3 |
|
r 4 |
|
|
2 sin ϕ |
|
π 16 |
|
4 |
|
|
4 |
|
π 4 |
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(2r sinϕ − r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= ∫dϕ |
|
∫ |
|
|
|
2sin |
ϕ |
|
|
|
− |
|
|
0 |
|
|
|
|
= ∫ |
|
|
|
sin |
ϕ − 4sin |
|
ϕ dϕ = ∫ |
|
sin ϕdϕ = |
||||||||||||||||||||||||
|
|
|
)dr = ∫dϕ |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
0 |
|
|||||||||
π |
4 |
|
1 − cos 2ϕ |
2 |
|
|
|
1 |
|
π |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
π |
|
|
|
|
|
|
|
|
|
1 + cos 4ϕ |
|
|
|
||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
dϕ |
= |
|
|
|
|
∫(1 − 2 cos 2ϕ + cos |
|
2ϕ)dϕ |
= |
|
|
|
∫ 1 |
− 2 cos 2ϕ + |
|
|
|
dϕ = |
|
|
|||||||||||||||||||||
3 |
|
|
|
2 |
|
|
3 |
|
|
3 |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
π |
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
− 2 cos 2ϕ + |
|
|
|
cos 4ϕ dϕ = |
|
|
|
ϕ −sin 2ϕ + |
|
|
sin 4ϕ |
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
3 ∫0 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
П = 8V = 8 π2 = 4π.
Ответы 4а и 4б совпали.
4в) Для определения циркуляции вектора F вдоль контура, полученного в результате пересечения поверхностей σ1 и σ2 ,каковым является пространственный эллипс (рис.3.36), необходимо вывести аналитическое выражение последнего в параметрической форме.
x = r cos t, y = r sin t, z = x2 |
+ y 2 = r 2 , z = 2 y = 2r sin t, r = 2sin t. |
Подставив значение |
r = 2sin t в выражение для x,y,z получим |
необходимое задание кривой интегрирования в параметрической форме.
141

x = r cos t
y = r sin t
z = 2 y =
=2sin t cost = 2sin 2t,
=2sin t sin t = 2sin 2 t,
2r sin t = r 2 = 4sin 2 t, 0 ≤ t ≤ π.
dx = 2 cos 2tdt, dy = 4sin t cos tdt, dz = 8sin t cos tdt.
Определим циркуляцию вектора F по данному контуру в направлении возрастания параметра t.
Ц = ∫F dl = ∫[(3x − y − z)i + 3y j + 2zk](dxi + dy j + dzk )= ∫(3x − y − z)dx + 2 ydy + 2zdz =
γ γ γ
= π∫[(3sin 2t − 2sin 2 t − 4sin 2 t)2 cos 2t + 3 2sin 2 t 4sin t cos t + 2 4sin 2 t 8sin t cos t]dt =
0 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
1 − cos 2t |
|
3 |
|
π |
|
1 |
+ cos 4t |
||
= ∫ |
3sin 4t −12 |
|
cos 2t +88sin |
|
t cos t dt = ∫ 3sin 4t − 6 cos 2t + 6 |
|
|
|
dt + |
|||
2 |
|
|
|
2 |
||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
||
|
|
π |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+88∫sin |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
π |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
td sin t = |
− |
|
|
|
|
cos 4t −3sin 2t |
+ 3t + |
|
|
|
sin 4t + 22sin |
|
t |
|
0 |
= 3π. |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
4 |
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4г) По формуле Стокса: Ц = ∫ |
|
|
|
|
|
|
|
ndS. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
F |
= ∫∫rotF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|
∂ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
rotF |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
∂x |
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3x − y − z 3y |
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
|
|
2z |
− |
|
3y i + |
|
|
|
|
|
(3x − y − z) − |
|
|
|
2z j + |
|
3y |
− |
|
|
(3x − y − z) k |
= − j + k . |
|||||||||||||||||||||||||||||
∂y |
∂z |
∂z |
|
∂x |
∂x |
∂y |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Здесь на контур циркуляции γ |
|
|
натянуты две поверхности: |
вектора F |
|||
σ1 - параболоид вращения z = x2+y2 |
и σ2 - плоскость z = 2y. Очевидно, что |
||
расчет циркуляции вектора F с помощью формулы Стокса как по одной так и по второй поверхности, приведет к одинаковому результату. Рассмотрим оба случая.
Случай 1. Пусть натянутой поверхностью будет σ1 , которая однозначно проектируется на плоскость z = 0. Выбор формулы (3.19) повторяется. В 4а)
|
|
|
− |
− − |
||
|
− |
|
2x i |
+ 2 y j−k |
|
|
определен вектор n1 |
= ± |
. Ещё раз напомним, циркуляция вектора |
||||
|
|
|||||
|
|
|
4x2 + 4 y2 +1 |
|||
− |
|
|
|
− |
||
F |
и направление вектора n1 должны соответствовать правилу винта. В |
|||||
142

нашем случае циркуляция |
− |
|
|
|
F происходит в сторону увеличения параметра t |
||||
|
|
− |
должен быть направлен во |
|
(рис. 3.36), тогда соответствующий вектор n1 |
||||
внутрь области V. В этом случае угол γ |
− |
^Oz) – острый, cosγ > 0 . В |
||
= ( n2 |
||||
− |
1 |
<0. Устраняем это несоответствие |
||
выражении для n1 , cosγ = − |
||||
4x2 + 4 y2 +1 |
||||
|
|
|
||
−
выбором знака «-» для n1 , тогда:
− |
− |
− |
n1 = . − 2 x i |
− 2 y j + k . |
|
− |
|
|
4 x 2 |
+ 4 y 2 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
− |
− |
|
−2x i+ |
2 y j+ k |
|
|
dxdy |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ц = ∫∫rotFn1ds = ∫∫rotFn |
|
|
|
|
|
= ∫∫ |
− j |
+ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫(2 y +1)dxdy = |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
σ1 |
|
|
|
|
|
|
|
|
|
|
|
σxy |
|
|
|
|
|
|
|
|
|
|
cosγ |
|
σxy |
|
|
|
|
4x |
|
+ 4 y |
|
|
+1 |
|
|
|
|
|
|
|
σxy |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y2 |
+1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= • |
|
• решаем как в 3а): r = 2sinϕ , 0 ≤ ϕ ≤ π , y = rsinϕ , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
π |
|
|
|
|
|
2 sin ϕ |
|
|
|
|
|
|
|
|
|
π |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
r2 |
|
|
2 sin ϕ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
dxdy = rdrdϕ • |
= |
|
∫dϕ |
|
∫ |
(2r sinϕ +1)rdr = ∫dϕ |
|
r |
sinϕ + |
= |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
= |
π |
|
16 |
sin |
4 |
ϕ + 2sin |
2 |
ϕ |
|
|
|
|
= |
π |
16 |
1 − сos2ϕ 2 |
|
2 |
1 − сos2ϕ |
|
|
|
|
|
= |
|
|
|
|
|||||||||||||||||||||||||||||||||
∫ |
|
3 |
|
|
|
|
|
|
dϕ |
∫ |
|
3 |
|
|
2 |
|
|
+ |
|
|
|
|
|
|
2 |
|
|
|
|
dϕ |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
4 |
(1 − 2 cos 2ϕ |
+ cos |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
∫ |
|
|
|
|
|
2ϕ) +1 − cos 2ϕ dϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
π |
|
4 |
− |
8 |
cos 2ϕ |
+ |
|
4 |
1 |
+ cos 4ϕ |
|
− cos 2ϕ |
|
|
|
π |
|
|
|
|
11 |
cos 2ϕ + |
2 |
cos 4ϕ |
|
||||||||||||||||||||||||||||||||||||
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
dϕ = |
|
3 − |
|
|
|
dϕ = |
||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
11 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
sin 2ϕ + |
sin 4ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3ϕ − |
|
6 |
6 |
|
|
= 3π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Случай |
2. |
|
|
|
|
Натянутая |
поверхность |
|
|
|
|
σ2 , |
как |
|
и |
σ1 , однозначно |
|||||||||||||||||||||||||||||||||||||||
проектируется на плоскость z = 0 в ту же область σxy . Так как направлению
циркуляции вектора |
− |
|
по контуру γ |
соответствует вектор |
− |
(рис.3.36), то |
|||||||||||||||||||||||||||||
F |
n2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
2 |
|
− |
1 |
− |
|
все дальнейшие рассуждения (см. 3а) приводят к вектору n2 |
= − |
|
|
j+ |
k . |
||||||||||||||||||||||||||||||
|
5 |
|
5 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
− |
|
dxdy |
|
|
|
|
|
|
|
|
|
2 − |
1 |
− dxdy |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ц = ∫∫rotF n2 ds = ∫∫rotF n2 |
|
|
|
|
|
= ∫∫(− j + k ) − |
|
j+ |
|
k |
|
|
|
|
|
= ∫∫3dxdy = |
|||||||||||||||||||
|
|
cosγ |
|
|
5 |
5 |
|
|
1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||
σ |
2 |
|
|
|
σ |
xy |
|
|
|
|
|
|
|
σ |
xy |
|
|
|
|
|
|
|
|
|
|
σ |
xy |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
143
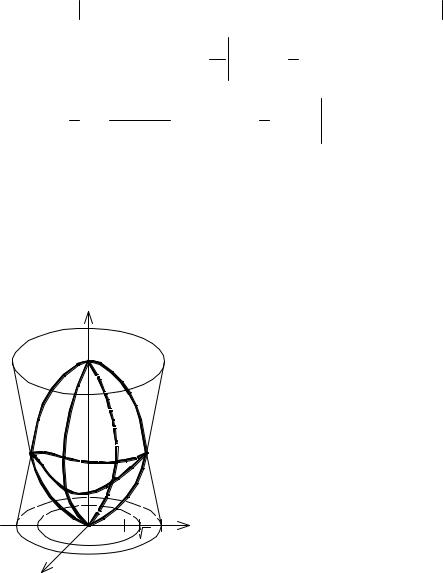
= • |
• Переход к полярным координатам – см. 3а • |
• |
= |
|
|||||||||||||
π |
|
2 sin ϕ |
|
π |
r2 |
2sinϕ |
= |
3 |
π |
|
2 |
ϕdϕ = |
|
|
|
|
|
= 3∫dϕ ∫ |
rdr = 3∫dϕ |
2 |
0 |
|
2 |
∫4sin |
|
|
|
|
|
||||||
0 |
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
||||
= 3 |
π |
4 1 − сos2ϕ dϕ = 3 |
ϕ |
− 1 sin 2ϕ π |
= 3π. |
|
|
|
|
||||||||
2 |
∫0 |
|
2 |
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
Ответы 4в) и 4г) совпали. |
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 5. Дано тело, полная поверхность которого образована двумя |
|||||||||||||||||
поверхностями II порядка σ1 и σ2 . Вычислить: |
|
|
|
|
|||||||||||||
а) |
поток |
векторного |
поля |
|
− |
|
|
|
|
|
поверхность |
тела в |
|||||
|
F через полную |
|
|||||||||||||||
z |
|
|
направлении внешней нормали к её поверхности |
||||||||||||||
|
|
|
|
непосредственно; |
|
|
|
|
|
||||||||
|
|
|
|
б) тот же поток – с помощью формулы |
|||||||||||||
|
|
|
|
Остроградского; |
|
|
|
|
|
|
|||||||
|
|
|
|
в) |
циркуляцию вектора |
− |
|
|
|
||||||||
|
|
|
|
F по замкнутому контуру, |
|||||||||||||
|
|
|
|
образованному пересечением поверхностей σ1 и σ2 |
|||||||||||||
|
|
|
|
непосредственно; |
|
|
|
|
|
||||||||
|
|
1 |
2 |
2 y г) ту же циркуляцию – с помощью формулы Стокса. |
|||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
− |
|
− |
|
− |
|
− |
σ1 : z = x2 + y2,σ2 : z = 4-3x2-y2. |
|
|||||||
|
|
F = (2x −3y) i |
+ 4 y j− z k , |
|
|||||||||||||
Решение. |
|
Тело |
представляет |
собой |
«яйцо» (рис.3.37), |
снизу |
|||||||||||
ограниченное параболоидом вращения z=x2+y2 (поверхность σ1), сверху – эллиптическим параболоидом z = 4-3x2-y2 (поверхность σ2). Кривая пересечения этих поверхностей есть «волнообразный» пространственный эллипс. В интересах дальнейших вычислений необходимо вывести формулы
−
для кривой пересечения поверхностей (контур циркуляции вектора F ) и её проекцию на плоскость z = 0.
144
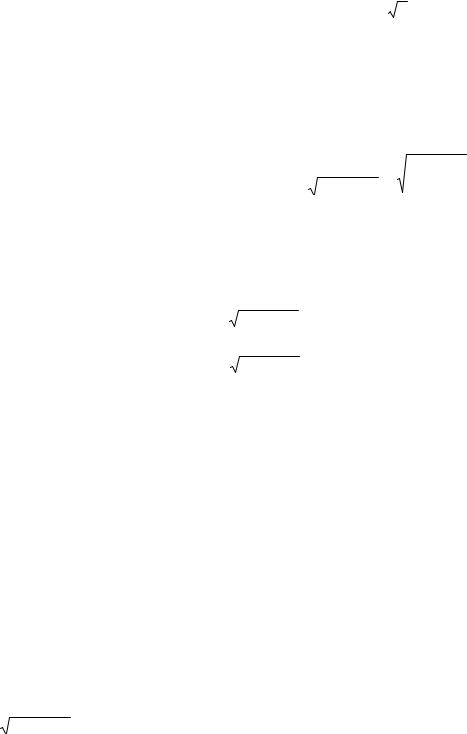
Приравнивая, левые и правые части уравнений поверхностей, находим аналитическое выражение для проекции кривой пересечения на плоскость z=0.
2 |
2 |
2 2 2 2 |
|
2 |
|
y2 |
|
x |
+y = 4-3x -y , 4x +2y = 4, |
x |
|
+ |
|
=1 |
|
|
( 2)2 |
||||||
Проекция кривой пересечения на плоскость z = 0 есть эллипс. В полярной системе координат формула эллипса представляет собой:
x = r cost, |
y = r sin t, r 2 cos2 t + |
1 |
r 2 |
sin 2 t =1; |
|
|
2r 2 cos 2 t + r 2 sin 2 t = 2 , r 2 |
+ r 2 cos 2 t = 2 , |
||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r 2 = |
|
|
2 |
= |
|
|
|
|
|
4 |
|
; |
r = |
|
2 |
|
= |
|
2 |
. |
|
|
|
|
|
|
||||||
|
|
1 |
+ cos2 t |
3 |
+ cos 2t |
|
|
|
1 + cos2 t |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|||||||||||||||
Теперь нетрудно получить формулу для контура циркуляции вектора |
||||||||||||||||||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = r sin t |
и z = x2+y2 = r2, то |
|||||||||||
F в параметрической форме. Т.к. x = r cost, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
= |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y |
= |
|
|
|
|
|
|
|
|
,0 |
≤ t ≤ 2π. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z |
= |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) |
Поток вектора |
|
|
− |
|
|
через |
|
|
|
полную |
поверхность |
тела равен: |
|||||||||||||||||||||
|
F |
|
|
|
|
|
||||||||||||||||||||||||||||
|
− − |
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П=П1+П2= ∫∫F n1 ds + |
∫∫F n2 ds . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
σ1 |
|
|
|
σ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обе поверхности и σ1 : z = x2+y2 и σ2 : z = 4-3x2-y2 однозначно |
||||||||||||||||||||||||||||||||||
проектируется |
только на |
плоскость |
z |
|
= |
0. Поэтому для расчета потоков |
||||||||||||||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− − |
||||||
вектора |
F П1 |
и П2 выбираем одну и туже формулу: П = ∫∫F n |
|
|
dxdy |
|
, где |
|||||||||||||||||||||||||||
|
|
cosγ |
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ xy |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
плоская область интегрирования σxy одна и та же и ограничена эллипсом
r = |
2 |
. |
3 + cos 2t |
−
Определим единичный нормальный вектор n1 для поверхности σ1 : z =
x2+y2
145

2 2 |
|
|
|
grad |
|
ϕ1 |
|
|
|
|
|
|
|
|||||
− |
|
|
|
|
|
2x i + 2 yj − k |
|
|
|
|||||||||
ϕ1 = x +y -z = 0, |
n1 |
=± |
|
|
|
|
|
= ± |
|
|
|
|
|
|
|
. . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
gradϕ1 |
4x2 + 4 y 2 + |
1 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||
По условию задачи поток вектора вычисляется в направлении внешней нормали к поверхности. Для поверхности σ1 этот вектор с осью Oz составляет
тупой угол (рис.3.37 ), т.е. |
cosγ – |
отрицательный. Для выполнения этого |
|||||||||||||||||||||
условия |
выбираем |
перед |
|
формулой |
|
для |
|
|
− |
знак + и тогда |
|||||||||||||
|
|
|
|
n1 |
|||||||||||||||||||
cosγ = − |
|
1 |
|
|
|
< 0 , что и требуется. |
|
|
|
|
|
|
|
|
|
|
|||||||
4x2 + 4 y 2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
− |
− |
|
− |
|
|
dxdy |
|
|||||
|
− − |
|
− |
|
− |
− |
2x i+ 2 y j− k |
|
|
|
|||||||||||||
П1 = ∫∫F n1 ds = |
∫∫ |
(2x −3y) i+ 4 y j− z k |
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||
|
|
|
|
2 |
|
2 |
|
|
|
1 |
|||||||||||||
|
σ1 |
|
σ1xy |
|
|
|
|
|
4x |
|
+ 4 y |
|
+1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y2 +1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫(4x2 |
− 6xy +8y 2 |
+ z)dxdy=• |
|
• z = x2 |
+ y 2 |
• |
|
• = ∫∫(4x2 |
− 6xy +8y 2 + x2 + y 2 )dxdy = |
||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
σ1xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1xy |
|
|
|
|
|
|
|
|
|
=∫∫(5x2 − 6xy + 9 y2 )dxdy =
σ1xy
=• • т.к. проекция σ1xy поверхности σ1 на плоскость xOy есть область
ограниченная эллипсом, для вычисления двойного интеграла целесообразно перейти к полярным координатам: x = r cost, y = r sin t,
0 ≤ r ≤ |
|
2 |
,0 ≤ t ≤ 2π • |
|
• = |
|
|
||||
|
+ cos 2t |
||||
3 |
|
2 |
|||
2 |
|
|
|
||
2π |
3+cos 2t |
|
= ∫dt |
∫(5r 2 cos2 |
|
00
−3r 2 sin 2t)rdr = 2∫π
0
|
|
|
|
|
|
|
|
2π |
3+cos 2t |
|
|
|
|
t − 6r 2 cos t sin t + 9r 2 sin 2 t)rdr = ∫dt |
|
∫(5r 2 + 4r 2 sin 2 t − |
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
r 4 |
|
|
2 |
|
2π 5 + 4sin 2 t −3sin 2t |
|
||||
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
3+cos 2t |
|
|
|||||
dt(5 + 4sin |
|
t −3sin 2t) |
|
|
|
|
|
= 4 |
∫ |
|
|
|
dt. |
|
4 |
|
|
|
|
(3 + cos 2t) |
2 |
||||||
|
|
|
|
|
0 |
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы решить этот определенный интеграл нужно применить подстановку tgt = q. Пределы интегрирования при новой переменной q
совпадут, т.к. при t = 0, tg0 = 0; при t = 2π, tg2π = 0. При этом нужно учесть,
что при изменении t от 0 до 2π в точках |
π |
и |
3 |
π тангенс не существует |
|
2 |
2 |
||||
|
|
|
146

(разрыв II рода), а определенный интеграл превращается в несобственный интеграл II рода. Строгая запись решения такого интеграла становится достаточно громоздкой.
Поступим так: найдем первообразную этого интеграла в новой переменной q без учета пределов (неопределенный интеграл), вернемся к старой переменной t, восстановим пределы интегрирования и произведем подсчёт.
|
|
|
|
4∫ |
5 |
|
+ 4sin 2 t −3sin 2t |
dt= |
• |
|
• tqt = q |
|
|
; |
|
dt = |
|
|
|
|
|
dq |
|
|
|
|
, |
|
sin t = |
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
, |
cos t = |
|
1 |
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(3 + cos 2t) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
|
|
|
q |
2 |
|
+1 |
q |
2 |
+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
sin 2t = |
|
|
|
2q |
|
|
|
, cos 2t |
|
= |
1 |
− q2 |
|
• |
|
• |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
+ q2 |
|
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
5 |
+ 4 |
|
|
q2 |
|
|
|
− |
3 |
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= 4∫ |
1 |
+ q2 |
|
|
1 |
+ q2 |
|
|
|
dq |
|
|
|
|
|
|
4∫ |
5(1 + q2 ) + 4q2 − 6q |
|
|
|
= ∫ |
|
9q2 |
|
− 6q + 5 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq = |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 − q |
2 |
2 |
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 + 2q |
2 |
2 |
(2 |
+ q |
2 |
) |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 + q |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= 9∫ |
|
|
q2 dq |
|
|
|
|
− 6∫ |
|
|
|
|
|
qdq |
|
|
|
|
|
+ 5∫ |
|
|
|
|
dq |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
) |
2 |
|
|
(2 |
2 |
) |
2 |
|
|
|
(2 + q |
2 |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
(2 + q |
|
|
|
|
|
|
|
|
|
|
|
+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Найдем первообразную каждого интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
dq |
|
|
|
|
= ∫ |
|
2 + q |
2 |
+ 2 |
− q |
2 |
|
|
|
|
|
|
1 |
|
∫ |
|
|
dq |
|
|
|
+ ∫ |
|
2 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 |
+ q |
2 |
) |
2 |
|
|
|
4(2 + q |
2 |
) |
2 |
|
|
|
|
4 |
2 + q |
2 |
|
(2 |
+ q |
2 |
) |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
2 |
∫d |
|
2 + q |
2 |
4 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 + q |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
qdq |
|
|
|
= |
|
1 |
∫ (2 + q2 )−2 d (2 + q 2 ) = − |
|
|
|
|
1 |
|
|
|
|
|
|
+ C. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
) |
2 |
2 |
|
2(2 + q |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
q 2 dq |
|
|
|
= ∫ |
|
q 2 + 2 − 2 |
|
dq = ∫ |
|
|
|
dq |
|
|
|
− 2∫ |
|
|
|
|
|
dq |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(2 |
+ q |
2 |
) |
2 |
|
|
(2 + q |
2 |
) |
2 |
|
2 |
+ q |
2 |
|
(2 + q |
2 |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
1 |
|
arctg |
|
q |
|
|
− 2 |
1 |
|
( |
|
1 |
arctg |
|
|
q |
|
|
+ |
|
|
|
q |
|
|
|
) |
|
+ C = |
|
1 |
|
arctg |
q |
|
|
|
− |
|
|
|
|
q |
+ C. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
4 |
|
|
|
2 |
|
|
|
2 |
|
|
2 + q2 |
|
|
2 |
|
2 |
|
|
|
|
|
2(2 + q2 ) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Для каждого интеграла вернемся к старой переменной t, восстановим пределы интегрирования и вычислим каждый интеграл.
147

2π |
|
dtgt |
|
|
|
|
||
∫ |
|
|
|
|
= |
|||
(2 + tg |
2 |
t) |
2 |
|||||
0 |
|
|
|
|
||||
+ |
1 |
arctg |
|
tgt |
||||
2 |
2 |
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
tgt |
|
|
|
|
tgt |
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
tgt |
|
|
π |
−0 |
|
|
tgt |
|
|
|
3 |
π −0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
2 |
1 |
|
|
|
2 |
|
|||||||||||||||||||||
|
|
arctg |
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
arctg |
|
|
+ |
arctg |
|
|
|
|
+ |
|||||||||||||||||||||||||
4 |
|
|
2 |
2 |
|
2 + tg |
2 |
t |
|
|
|
|
|
4 |
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
π |
+0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2π |
|
|
tgt |
|
|
|
π |
−0 |
|
|
|
tgt |
|
|
|
|
|
π −0 |
|
|
|
tgt |
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
+ |
|
|
|
|
2 |
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||
|
|
3 |
|
π +0 |
|
2 + tg 2t |
|
|
|
|
|
|
2 |
+ tg 2t |
|
|
π |
|
|
|
|
2 + tg 2t |
|
|
3 |
π +0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
π |
|
|
|
|
|
|
|
|
|
1 π |
|
|
|
|
π |
|
|
|
|
|
1 |
|
|
|
|
π |
|
|
|
|
= |
1 2 |
π |
|
= |
|
π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
− 0 |
+ |
|
|
|
|
|
|
|
|
− |
− |
|
|
+ |
|
|
|
|
0 − |
− |
|
|
+ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
4 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
4 2 |
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
2π tg td tg t |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2π |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
π |
−0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
π −0 |
|
|
1 |
|
|
|
2π |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
2 |
|
+ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫0 (2 + tg |
2 |
t) |
2 |
|
2(2 |
|
+ tg |
2 |
t) |
|
|
2 |
|
(2 |
+ tg |
2 |
t) |
|
|
|
|
(2 + tg |
2 |
t) |
|
|
|
|
|
|
(2tg |
2 |
t) |
|
3 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
+0 |
|
|
|
|
|
π +0 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= − |
|
|
0 − |
|
|
|
|
+ 0 + |
|
|
|
− 0 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2π |
|
tg 2 td tg t |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
tg t |
|
|
|
tg t |
|
|
|
|
2π |
|
|
1 |
|
|
2π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
|
|
|
|
arctg |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
) |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
(2 + tg |
2 |
|
|
t) |
2 |
|
2 |
2 |
|
|
|
2 |
2(2 + tg |
2 |
t) |
0 |
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
(Здесь опушены несложные пределы). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Окончательно определяем поток П1 |
|
вектора |
|
|
− |
через поверхность σ1: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
F |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
П1= 9 |
π |
|
|
|
−6 0 + 5 |
|
|
π |
|
|
= |
|
|
23π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
−
Определяем единичный нормальный вектор n2 для поверхности σ2 :z = 4-3x2-y2.
|
|
|
|
|
|
|
|
|
|
|
− |
− |
− |
|
|
|
ϕ2 = 3x2 + y2 + z − 4 = 0 , n2 |
= ± |
|
grad |
ϕ2 |
|
|
= ± |
|
6x i |
+ 2 y j+ k |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
gradϕ2 |
|
|
|
|
36x2 + 4 y 2 |
+1 |
|
|
|
||
Для поверхности |
σ2 |
внешняя |
нормаль |
− |
составляет с |
осью |
Oz |
|||||||||
( n2 ) |
||||||||||||||||
острый угол (рис.3.37), |
т.е. |
cos γ – положительный. В формуле |
для |
− |
||||||||||||
n2 |
||||||||||||||||
выбираем знак + и тогда cosγ = |
1 |
|
|
|
|
тоже положительный. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
36x2 + 4 y 2 +1 |
|
|
|
|
|
||||||||
148

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
− |
|
dxdy |
|
|
|
|
||||
|
|
|
|
|
− |
− |
|
|
|
|
|
|
− |
|
|
|
− |
− |
6x i |
+ 2 y j+ k |
|
|
|
|
|
|||||||||||||||||
П2 = ∫∫F n2 ds = |
∫∫ |
(2x − |
3y) i |
+ 4 y j− z k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
σ2 |
|
|
|
|
σ2 xy |
|
|
|
|
|
|
|
|
|
|
36x |
|
|
+ 4 y |
|
+1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36x2 + 4 y 2 |
+1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫∫(12x2 |
|
−18xy + 8y 2 |
− z)dxdy=• |
|
• z = 4 − 3x2 − y 2 |
• |
|
• |
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
σ2 xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫∫(12x2 |
|
−18xy + 8y 2 |
− 4 + 3x2 + y 2 )dxdy = ∫∫(15x2 |
|
−18xy + 9 y 2 − 4)dxdy = |
|||||||||||||||||||||||||||||||||||||
σ2 xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ2 xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
=• |
|
|
• производим такой же переход к полярным координатам • |
|
|
• = |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2π |
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
3+cos 2t |
|
|
|
|
|
|
|||||||||
= ∫dt |
∫(15r 2 cos2 t −18r 2 cos t sin t +9r 2 sin 2 t −4)rdr = ∫dt |
|
|
∫ |
(9r 2 |
+6r 2 cos 2 t − |
|
|
|
|
||||||||||||||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
3+cos |
2t |
|
|
|
|
|
|
|
|
|
|||||||||
−9r |
|
sin 2t |
−4)rdr = |
dt (9 +6 cos |
|
t − |
9 sin 2t) |
|
|
− 2r |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2π |
9 +6 cos |
2 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= ∫ |
|
|
|
t −9 sin 2t |
4 − |
|
|
|
|
dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(3 +cos 2t) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для вычисления этого определенного интеграла поступим таким же образом, как в предыдущем случае.
|
|
|
9 + 6cos |
2 |
t −9sin 2t |
|
|
|
|
|
|
8 |
|
|
|
|
• |
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∫ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
dt= |
• tgt = q • |
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(3 + cos 2t) |
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
9 + 6 |
|
|
|
|
−9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1+ q2 |
|
|
|
8 |
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= ∫ |
|
4 |
|
|
1+ q2 |
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
1− q |
2 |
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1− q |
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
|
1 |
+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
9(1+ q |
2 |
) + 6 −18q |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
q |
2 |
dq |
|
|
|
|
qdq |
|
|
dq |
|
|
|
dq |
|
|||||||||||||||
= |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
dq = 9 |
|
|
|
|
−18 |
|
+15 |
|
− 4 |
|
|
. |
||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
∫(2 + q2 )2 |
|
|
∫2 |
|
||||||||||||||||
|
|
|
2 2 |
|
2 + q2 |
2 |
|
|
|
2(2 |
+ q2 ) |
|
|
|
(2 + q2 )2 |
|
∫(2 |
+ q2 )2 |
|
+ q2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
(1+ q ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Все интегралы вычислены ранее, кроме последнего:
∫ |
|
dq |
|
= |
1 |
arctg |
q |
+ C; |
2∫π |
dtgt |
|
= |
1 |
arctg |
tgt |
2 |
+ q |
2 |
2 |
2 |
2 |
t |
2 |
2 |
|||||||
|
|
|
|
|
0 2 + tg |
|
|
||||||||
2π
0
= 2π2 .
Определяем поток П2:
П2 = 9 π2 −18 0 +15 2π2 − 4 2π2 = 172 π2 .
−
Определяем поток вектора F через полную поверхность:
149

П = П1 + П2 = |
23π |
+ |
17π |
= |
40π |
=10 2π. |
||||
2 |
2 |
2 |
2 |
2 |
2 |
|||||
|
|
|
|
|||||||
−
б)Поток вектора F через полную поверхность тела по формуле
Остроградского: П = ∫∫∫divFdV .
V
Определим дивергенцию вектора |
|
− |
: |
|
|
|
|||||
F |
4 y + ∂ (−z) = 2 + 4 −1 = 5 . |
||||||||||
div F = ∂Fx |
+ ∂Fy |
+ ∂Fz = ∂ |
(2x −3y) + ∂ |
|
|
||||||
− |
|
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
∂z |
∂x |
|
|
∂y |
|
|
∂z |
|
|
Тройной интеграл вычислим в цилиндрической системе координат:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4−3x2 −y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
3+cos 2t |
|
|
|
4−2r 2 cos2 t −r 2 |
|
|||||||||||||||||||||||||||||
П = ∫∫∫div F dV |
= 5 ∫dt |
|
∫rdr |
∫dz=• |
|
• x = r cos t, y = r sin t • |
|
• |
|
= 5 ∫dt |
|
|
∫rdrz |
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x2 +y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2π |
|
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 5 |
∫dt |
|
|
∫ |
(4 − 2r 2 cos2 t − r 2 |
|
− r 2 )rdr = 5 ∫dt |
|
|
|
∫(4r − 2r 3 cos2 t − 2r 3 )dr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2π |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2π |
|
8 |
|
|
|
|
|
|
|
|
|
8cos |
2 |
t |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= 5 ∫dt |
2r |
|
|
− |
|
|
|
|
|
r |
|
cos |
|
|
t − |
|
|
r |
|
|
|
|
|
|
|
|
= 5 ∫ |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
dt. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
3 + cos 2t |
|
(3 |
+ cos 2t) |
2 |
|
(3 + cos 2t) |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Вычислим этот интеграл, как это делалось в а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8cos |
2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
= |
|
|
|
•tgt = q |
• |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
+cos 2t |
(3 +cos 2t) |
2 |
(3 +cos 2t) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 5∫ |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
1+ q |
2 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
dq |
|
= 5∫ |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
8(1+ q |
2 |
) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
dq = |
|||||||||||||||||||||||
|
|
|
|
1−q |
2 |
|
|
|
1 |
−q |
2 |
2 |
|
|
1−q |
|
2 |
2 |
|
1+ q |
2 |
|
|
|
|
|
2 |
) |
4(2 |
+ q |
2 |
) |
2 |
|
4(2 + q |
2 |
) |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(2 + q |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1+ q |
|
|
|
|
|
1 |
+ q |
2 |
|
|
|
|
|
|
|
1+ q |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= 5∫ |
8 + 4q2 −2 −2 −2q |
2 |
|
dq = 5∫ |
|
|
|
2q2 + 4 |
|
dq =10∫ |
|
dq |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
(2 + q2 )2 |
|
|
|
|
|
|
(2 + q2 )2 |
2 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Воспользуемся решением этого интеграла в а).
П =10 |
2π |
=10 2π. |
|
2 |
|||
|
|
Как и следовало ответы а) и б) совпали.
−
в) Циркуляция вектора F по замкнутому контуру γ :
−−
Ц= ∫F dl .
r
150

Аналитическое выражение для контура γ |
в параметрической форме: |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
= |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
+ cos 2t |
|
|
|
|
|
|
(−2) sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
(−2sin t) |
|
|
|
3 + cos 2t − 2 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 + cos 2t |
|
|
(−2sin t)(3 + cos 2t) + 2 cos t sin 2t |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt = |
dt. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3 + cos 2t)3 |
|||||||||||||
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
γ : |
y |
= |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
+ cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 cost |
3 + cos 2t − 2sin t |
|
(−2) sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos t(3 + cos 2t) + 2sin t sin 2t |
|
|
||||||||||||||||||||||||||||
|
|
|
|
dy = |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 + cos 2t |
|
|
dt = |
dt. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3 + cos 2t)3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
(−4)(−2) sin 2t |
|
|
|
|
|
8sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
z |
= |
|
|
|
|
|
|
|
|
, |
|
|
dz = |
dt == |
|
|
|
|
dt. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
+ cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
(3 + cos 2t)2 |
|
|
|
(3 |
+ cos 2t)2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
0 |
≤ t ≤ 2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
− |
− |
− |
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ц = ∫Fdl |
|
|
|
|
= ∫ (2x |
−3y) i |
+ 4 y j− z k (dx i+ dy j+ dz k) |
= ∫(2x −3y)dx + 4 ydy −zdz = |
|
||||||||||||||||||||||||||||||||||||||||
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||
=• |
|
|
• переход к параметрической форме • |
|
• |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2π |
|
|
|
|
|
2 cost |
|
|
|
|
|
|
|
2sin t |
(−2sin t)(3 + cos 2t) + 2 cos t sin 2t |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||
|
∫ |
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
|
|
|
|
|
(3 + cos 2t) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2sin t |
|
2 cos t(3 |
+ cos 2t) + 2sin t sin 2t |
|
|
|
|
|
|
4 |
|
|
|
|
8sin 2t |
|
|
|
|
||||||||||||||||||||||||
+ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt. |
|
||||||
3 + cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + cos 2t |
(3 + cos 2t) |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3 + cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При решении этого интеграла повторим алгоритм решения в пункте а).
∫ |
|
4 cos t |
|
(−2 sin t)(3 + cos 2t) + 2 cos t sin 2t |
dt |
|||||||
|
3 + cos 2t |
|
|
|
|
(3 + cos 2t) 3 |
|
|
||||
− ∫ |
6 sin t |
|
|
|
|
(−2 sin t)(3 + cos 2t) + 2 cos t sin 2t |
||||||
3 + cos 2t |
|
|
|
(3 + cos 2t) |
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
+ ∫ |
8 sin t |
|
|
|
|
2 cos t(3 |
+ cos 2t) + 2 sin t sin 2t |
dt |
||||
3 + cos 2t |
|
|
|
(3 + cos 2t) |
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
− |
|
|
|
|
|
|
|
|
|
dt + |
|
|
|
|
|
|
|
|
|
− ∫ |
|
32 sin 2t |
|
dt =• |
|
• tgt = q, dt = |
dq |
|
, |
|
|
|
|||||||
(3 |
+ cos 2t) |
3 |
1 + q |
2 |
|||||
|
|
|
|
|
|
|
|||
sin t = |
|
|
q |
|
|
|
|
, cos t = |
|
|
1 |
|
|
, sin 2t = |
|
|
2q |
|
, cos 2t = |
1 − q 2 |
|
• |
|
• |
= |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 + q 2 |
|
|
1 + q 2 |
|
1 |
+ q 2 |
1 + q 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2q |
|
|
|
|
|
1 − q |
2 |
|
|
|
|
1 |
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
3 |
+ |
|
|
|
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
+ q |
2 |
|
|
|
|
|
|
1 + q |
2 |
|
1 |
+ q |
2 |
|
1 + q |
2 |
1 |
+ q |
2 |
|
|
|
|
dq |
|
|
|||||||||||||||||
= ∫ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|||||||||||||||||
3 + |
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− q |
2 |
|
3 |
|
|
|
|
|
|
|
1 |
+ q |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
151
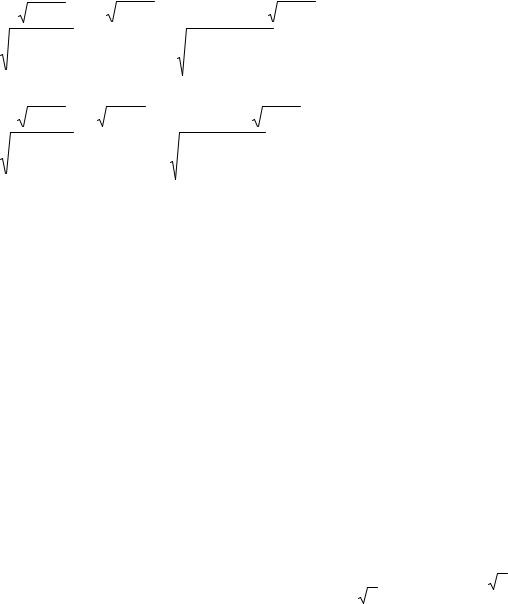
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
1 |
− q |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
3 + |
|
|
|
|
+ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
− q |
2 |
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
1 |
+ q |
2 |
|
1 + q |
2 |
1 |
+ q |
2 |
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
− ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
3 + |
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
− g |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
+ g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
− q |
2 |
|
|
|
|
|
|
q |
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
1 |
+ q 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q |
2 |
|
1 + q 2 |
1 |
+ q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q 2 |
|
|
|
|
|
|
|
|
dq |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
|
|
|
|
1 |
− q |
2 |
3 |
|
1 |
+ q |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= ∫ |
4( |
−8q − 4q 3 |
|
+ 4q)dq |
|
|
−∫ |
6(−8q 2 |
− 4q 4 |
+ 4q 2 )dq |
|
+∫ |
8(8q + 4q 3 |
|
+ 4q 3 )dq |
−∫ |
64q(1 + q 2 )dq |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4(2 |
|
+ q |
2 |
) |
2 |
|
(1 + q |
2 |
) |
|
|
|
|
4(2 + q |
2 |
) |
2 |
(1 + q |
2 |
) |
|
|
|
4(2 |
+ q |
2 |
) |
2 |
|
(1 + q |
2 |
) |
|
|
|
|
|
|
8(2 + q |
2 |
) |
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= ∫ |
|
− 4qdq |
|
|
|
+ ∫ |
|
|
|
6q 2 dq |
|
|
−∫ |
|
16qdq |
|
|
|
|
−∫ |
|
8q(1 + q 2 )dq |
= 6 |
∫ |
|
|
|
q 2 dq |
|
|
|
|
+12∫ |
|
|
qdq |
|
|
|
|
|
− |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2 |
|
+ q |
2 |
) |
2 |
|
(2 |
+ q |
2 |
) |
2 |
|
(2 |
+ q |
2 |
) |
2 |
|
|
|
(2 + q |
2 |
|
) |
3 |
|
|
|
(2 |
+ q |
2 |
) |
2 |
|
(2 |
+ q |
2 |
) |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
− 8∫ |
(q + q 3 )dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(2 + q |
2 |
) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Первые два интеграла вычислены в пункте а). Вычислим последний интеграл:
∫ |
(q + q3 )dq |
= ∫ |
|
qdq |
|
|
+ ∫ |
|
q3 dq |
|
|
|
|
|
|
1 |
∫(2 |
+ q |
2 |
|
|
−3 |
d (2 + q |
2 |
|
|
|
|
1 |
∫ |
q2 + 2 − 2 |
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
) |
|
|
|
|
) |
+ |
|
|
|
|
|
|
|
|
|
d(2 |
+ q |
|
) = |
|||||||||||||||||||||
(2 + q |
2 |
) |
3 |
(2 |
+ q |
2 |
) |
3 |
(2 + q |
2 |
) |
3 |
2 |
|
|
|
|
|
|
|
2 |
(2 + q |
2 |
) |
3 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= − |
1 |
∫(2 |
+ q2 )−3 d (2 + q |
2 ) + |
1 |
∫(2 + q2 )−2 d (2 + q2 ) = |
|
1 |
|
|
|
|
|
− |
|
|
1 |
|
|
|
|
+ C. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
) |
2 |
|
2(2 + q |
2 |
) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4(2 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
При восстановлении переменной t и пределов интегрирования эти |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегралы сводятся к нулю (см. пункт а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Окончательно циркуляция вектора: Ц = 6 |
π |
|
|
+12 0 −8 0 = 3 2π. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
г) Циркуляция вектора |
|
|
по формуле Стокса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ц= ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rot |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
ndS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
∂ |
|
|
= 3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rot |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x −3y |
|
4 y |
|
|
|
− z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
На контур γ натянуты обе поверхности σ1 и σ2, которые однозначно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
проектируются |
на |
|
плоскость |
|
|
z |
= |
|
|
|
|
|
0, |
|
|
образуя |
|
|
известную |
область |
|||||||||||||||||||||||||||||||||||||||||||||||
152
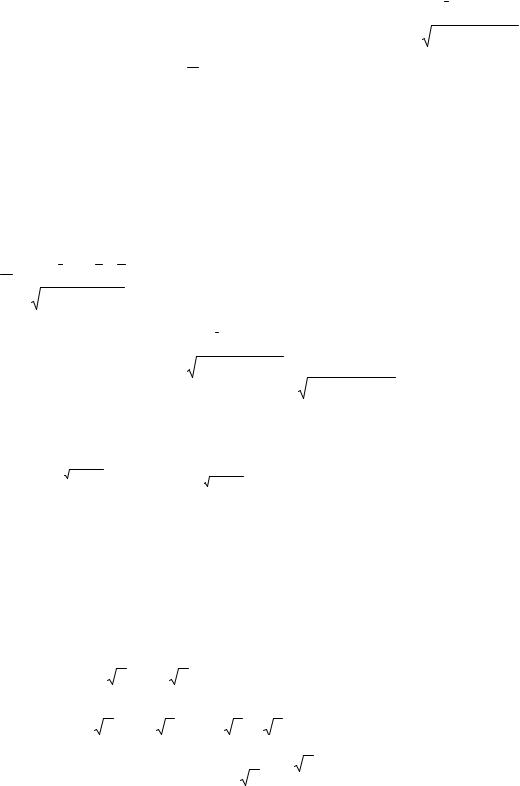
интегрирования, ограниченную эллипсом. Произведём расчёт циркуляции с использованием обеих поверхностей.
2 2 |
2 2 |
|
|
|
grad |
ϕ1 |
|
|
2xi + 2 y |
j |
− |
k |
|
|
|
|
|
|
|
||||||||||
Для σ1: z = x +y , φ1 |
= x +y -z = 0, |
n1 = ± |
|
|
|
|
= ± |
|
. |
|||||
|
|
ϕ1 |
|
4x2 + 4 y 2 +1 |
||||||||||
grad |
|
|||||||||||||
Циркуляция вектора F по замкнутому контуру γ в сторону увеличения параметра t происходит против часовой стрелки, если смотреть на этот контур сверху (рис.3.37). Согласно правила винта единичный нормальный вектор к поверхности σ1 в этом случае направлен во внутрь (нормаль внутренняя) и должен составлять с осью Оz острый угол и cosγ>0. Это условие в формуле для n1 выполнится, если выбрать перед формулой знак «-»,
т.е. n1 = −2xi −2 y j + k .
4x2 + 4 y2 +1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2xi − 2 y j |
+ k |
|
|
dxdy |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ц= ∫∫rot F n1dS = ∫∫3k |
|
|
|
|
|
|
= ∫∫3dxdy = |
|
|
||||||||||||||||||||||||||
|
|
|
4x |
2 |
+ 4 y |
2 |
+1 |
|
|
|
1 |
|
|
|
|
||||||||||||||||||||
|
|
σ1 |
|
|
|
|
σ1xy |
|
|
|
|
|
|
|
|
|
|
|
σ1xy |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y 2 +1 |
|
|
|||||
=• |
|
• переход к полярной системе координат: |
x = r cos t, y = sin t • |
|
• = |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
2π |
2 |
|
|
2π |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3+cos 2t |
|
r |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3+cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= 3 ∫dt |
|
∫ |
rdr = 3 ∫dt |
|
|
|
= |
6 ∫ |
|
|
dt. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
+ cos 2t |
|
|
|
|
|
|||||||||||||||||||||
|
0 |
|
0 |
|
|
0 |
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методика расчёта этого интеграла такая же как в а).
∫ |
|
|
|
dt |
= |
• |
|
• tg |
|
= q, dt = |
|
|
dq |
|
|
;cos 2t = |
1 − q2 |
• |
|
• |
= ∫ |
|
|
|
|
dq |
|
|
|
|
|
= ∫ |
|
dq |
|
= |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3 + cos 2t |
|
|
1 + q |
2 |
1 + q |
2 |
|
|
|
1 − q |
2 |
|
|
|
2 |
|
|
4 |
+ 2q |
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+ |
|
|
|
|
(1 |
+ q |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
1 |
|
∫ |
|
dq |
|
|
|
= |
|
1 |
|
|
1 |
arctg |
|
q |
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
2 + q |
2 |
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
2π |
|
dtgt |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
tgt |
|
|
2π |
|
|
|
2π |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∫0 |
|
|
= |
|
|
|
|
arctg |
|
|
|
|
0 |
|
|
= |
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
2 + tg 2t |
2 |
|
2 |
|
2 |
|
|
|
2 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Циркуляция вектора: Ц = 6 |
π |
= 3 2π. |
|
2 |
|||
|
|
||
Для σ2 : |
|
|
153
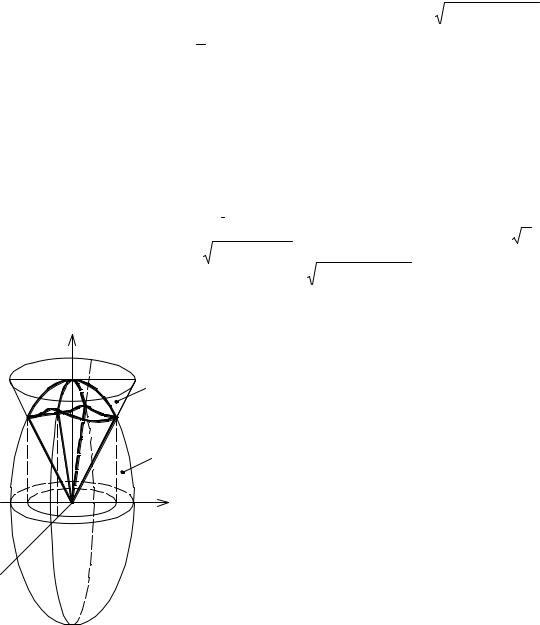
|
|
|
grad |
ϕ2 |
|
|
|
|
|
|
|
|
z = 4 −3x2 − y 2 ,ϕ2 = 3x2 + y 2 + z − 4 = 0; n2 |
= ± |
|
|
= ± |
6xi |
+ 2 yj + k |
. |
|||||
|
|
|
|
|
|
|||||||
|
|
|
gradϕ2 |
|
|
36x2 + 4 y 2 +1 |
||||||
Циркуляция вектора F по замкнутому контуру γ в сторону увеличения
параметра t определяет по правилу винта то же самое расположение вектора
n2 |
на внешней стороне поверхности σ2 |
(нормаль внешняя), тогда угол между |
|||||||||||||||||||||
n2 |
и осью Oz острый, |
cos γ > 0, значит в формуле для n2 |
нужно выбрать знак |
||||||||||||||||||||
«+». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6xi + 2 y j + k |
dxdy |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Ц = ∫∫rotF n2 dS = ∫∫3k |
|
|
|
= |
∫∫3dxdy = 3 2π, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
36x |
2 |
4 y |
2 |
+1 |
|
1 |
|
|||||||||||||||
|
σ2 |
σ2 xy |
|
|
|
|
|
|
|
σ2 xy |
|||||||||||||
|
|
|
|
36x2 + 4 y 2 +1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z
σ1
σ2
y
 x
x
Рис. 3.38
σ2 образуется контур
т.к. σ1xy = σ2 xy .
Все циркуляции, определяемые разными формулами, совпали.
|
|
|
|
|
− |
Пример 6. Вычислить циркуляцию вектора F |
|||||
вдоль |
контура |
γ |
образованного |
пересечением |
|
кругового конуса σ1 и эллипсоида σ2: |
|
||||
а) непосредственно; |
|
|
|||
б)с помощью формулы Стокса. |
|
||||
− |
|
− |
− |
− |
σ1:z2=x2+y2, |
F |
= ( 2 x − |
y ) i |
+ ( x − 2 y ) j + z k |
||
σ2 :z=9-3x2-6y2.
Решение. При пересечении поверхностей σ1 и
– пространственный «волнообразный» эллипс
−
(рис.3.38). Для определения циркуляции вектора F вдоль данного контура необходимо вывести аналитическую формулу этого контура в параметрической форме.
x = r cost, y = r sin t, z 2 = x 2 + y 2 = r 2 cos 2 t + r 2 sin 2 t = r 2 , z = r ;
Осталось выразить r через параметр t:
154
z2 = 9 −3x2 −6 y2 , r2 = 9 −3r2 cos2 t −6r2 sin2 t, r2 = 9 −3r2 −3r2 sin t,
4r 2 |
+ 3r 2 sin 2 t = |
9, r 2 = |
|
|
|
9 |
|
|
= |
|
|
|
|
9 |
|
|
|
= |
|
18 |
|
|
|
, |
|
|
|
|||||||||||
4 |
|
+ 3sin 2 |
t |
4 |
+ |
3 |
1 |
− cos 2t |
11 −3cos 2t |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r = |
18 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
11 −3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Одновременно |
|
|
это |
есть |
уравнение |
|
|
эллипса |
|
– проекции контура |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
на плоскость z = 0. |
|
|
|
|
|
|
|
|
|||||||||||||||
циркулирования вектора F |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Выражения для самого контура следующие: |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−sin t) |
11 −3cos 2t − |
|
cos t 6 sin 2t |
|
||||||||||||
|
|
x |
= |
|
|
|
|
|
18 |
|
|
|
|
cost, dx = |
|
18 |
2 11 −3cos 2t |
dt = |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
11 |
−3cos 2t |
|
|
|
|
|
|
|
|
|
11 −3cos 2t |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
18 |
(−sin t)(11 −3cos 2t) −3cos t sin 2t |
dt. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
11 −3cos 2t |
− |
sin t 6 sin 2t |
|
|
|
||||||||||
|
|
y |
= |
|
|
|
|
|
18 |
|
|
|
|
sin t, dy = |
|
18 |
2 11 −3cos 2t |
dt = |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
11 −3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 −3cos 2t |
|
|
|
|
|
|||||||||||||
|
= |
18 |
cos t(11 −3cos 2t) −3cos t sin 2t |
dt. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
(−3) 2(−sin 2t) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
z |
= |
|
|
|
|
|
18 |
|
|
|
|
, dz = |
18 |
|
|
2 |
11 −3cos 2t |
|
|
dt = |
18 |
|
|
(−3sin 2t) |
dt |
|||||||||||
|
|
11 |
−3cos 2t |
|
|
|
|
|
|
|
|
(11 −3cos 2t)3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 −3cos 2t |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
0 ≤ t ≤ 2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
определяется: |
|
||||||
|
|
а) Непосредственно циркуляция вектора F |
|
|||||||||||||||||||||||||||||||||||
|
|
− |
|
|
− |
+ |
|
|
|
− |
|
|
|
− |
|
|
− |
|
− |
|
|
|
− |
∫(2x |
− y)dx + (x − 2 y)dy + zdz |
|||||||||||||
Ц = ∫Fdl = ∫ (2x − y) i |
(x − 2 y) j+ z k (dx i+ dy j |
+ dz k) = |
||||||||||||||||||||||||||||||||||||
|
γ |
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|||||||
Вычисляем каждый из пяти интегралов отдельно.
|
2π |
18 |
|
|
(−sin t)(11 −3cos 2t) −3cos t sin 2t |
|
||
∫xdx = |
∫ |
cos t 18 |
|
dt. |
||||
11 − 3cos 2t |
(11 − 3cos 2t) |
3 |
||||||
γ |
0 |
|
|
|
|
|||
Вычисление этого и последующих интегралов произведём таким же образом, как в предыдущем примере 5а).
155

tgt = q, dt = |
|
|
dq |
|
, cos t = |
|
|
1 |
|
|
,sin t = |
|
|
|
q |
|
, cos 2t = |
1 |
− q2 |
,sin 2t |
= |
|
|
2q |
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 + q2 |
|
|
+ q2 |
|
|
|
1 |
|
|
|
1 |
+ q2 |
|
1 + q2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
+ q2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
18cos t |
|
|
|
|
|
(−sin t)(11 −3cos 2t) −3cos t sin 2t |
dt |
=18∫ |
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
11 |
−3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
11 −3 |
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
q |
|
|
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 + q2 |
|
11 −3 |
1 + q |
2 −3 |
|
|
|
1 |
+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q2 |
|
|
dq |
|
|
|
(−q)(8 +14q |
2 |
) − 6q |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=18∫ |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
= |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 + q2 |
|
(8 +14q2 )2 (1 + q2 ) |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
11 − |
1 |
+ q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=18∫ |
(−14)q(1 + q2 ) |
|
dq = −18∫ |
|
|
14qdq |
|
|
= −9∫(8 +14q |
2 |
) |
−2 |
d |
(8 +14q |
2 |
) |
= |
|
|
|
9 |
|
|
. |
|||||||||||||||||||||||||||||||||||||||
(8 +14q |
2 |
)(1 |
+ q |
2 |
) |
(8 +14q |
2 |
) |
2 |
|
|
|
|
|
8 |
+14q |
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Возвращаемся |
|
к |
|
|
|
|
|
переменной |
|
|
|
t |
|
|
с восстановлением |
|
|
пределов |
|||||||||||||||||||||||||||||||||||||||||||||
интегрирования
2π |
|
|
14tgtdtgt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
π |
−0 |
|
|
|
|
|
|
|
|
|
3 |
π −0 |
|
|
|
|
|
|
|
2π |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|
|
2 |
|
|
9 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
−18 ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
(8 +14tg |
2 |
t) |
2 |
|
8 |
+14tg |
2 |
t |
|
8 |
+14tg |
2 |
t |
|
8 |
+14tg |
2 |
t |
π |
8 |
+ |
14tg |
2 |
t |
|
|
3 |
|||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+0 |
|
|
π +0 |
|||||||||||||||||||||||||||||||||||||
= 0 − |
9 |
+ 0 − 0 + |
9 |
|
− 0 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2π |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
cos t(11 |
− 3cos 2t) |
− 3sin t sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∫ ydy = ∫ |
|
|
|
|
|
|
|
|
|
sin t |
18 |
|
dt. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
11 |
− 3cos 2t |
|
|
|
|
|
(11 − 3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
γ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
tgt = q, dt = |
|
dq |
|
|
, cos t = |
|
|
1 |
|
|
|
, sin t = |
|
q |
, cos 2t = |
1 |
− q 2 |
, sin 2t = |
|
2q |
|
|
. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
+ q 2 |
|
|
1 + q 2 |
1 + q 2 |
1 |
+ q 2 |
1 + q 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
q
∫ |
18 sin t |
|
|
|
|
cos t(11 − 3cos 2t) − 3sin t sin 2t |
dt |
=18∫ |
||||||||||||||||||||||||||||||
11 |
− 3cos 2t |
|
|
|
|
|
|
|
(11 − 3cos 2t) |
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
|
q |
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
− |
3 |
|
|
2 |
|
− 3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
11 |
1 + q |
|
|
1 + q 2 |
+ q |
|
|
|
|
|
|
dq |
|
|
|||||||||||||||||||
|
|
|
1 + q 2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
= 18∫ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
+ q |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
11 − 3 |
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 18∫ |
|
8q(1 + q 2 ) |
|
|
|
|
dq = 18∫ |
|
|
8qdq |
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||
(8 +14q |
2 |
) |
2 |
(1 + q |
2 |
) |
(8 |
+14q |
2 |
) |
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 + q 2 |
|
|
||||
|
1 |
− q 2 |
|
|||
11 − 3 |
|
|
||||
|
|
|
|
|
||
1 |
+ q 2 |
|
|
|||
|
|
|
||||
q(8 +14q 2 − |
6q 2 ) |
dq = |
||||
(8 +14q 2 ) 2 (1 + q 2 ) |
||||||
|
||||||
156

Такой интеграл уже решен ранее и его конечный результат равен нулю.
|
2π |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−3) sin 2t |
|
|
|
|
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∫zdz = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
11 − 3cos 2t |
|
|
|
|
|
(11 − |
3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
γ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Такие |
|
же |
|
|
|
|
вычисления |
|
|
|
приводят |
|
|
и |
|
|
|
этот |
|
|
|
|
интеграл |
|
|
|
к |
нулю. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2π |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cost(11 −3cos 2t) −3sin t sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
∫xdy = ∫ |
|
|
|
|
|
|
|
|
|
|
|
cost |
|
18 |
dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11 −3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
γ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Производим аналогичные действия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
18cos t |
|
|
|
|
|
cos t(11 −3cos 2t) −3sin t sin 2t |
|
dt |
= |
18∫ |
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
11 |
−3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
11 −3 |
1 − q |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
1 + q2 |
|
|
1 + q |
2 |
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
(8 +14q2 − 6q2 ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
18∫ |
|
|
dq = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 + q |
2 |
|
|
|
(8 +14q |
2 |
) |
2 |
(1 + q |
2 |
) |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 −3 |
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
=18∫ |
|
|
8(1 + q2 ) |
|
|
|
|
|
|
|
|
|
|
=144∫ |
|
|
|
|
|
dq |
|
|
|
|
|
=144∫ |
|
8 +14q2 |
+8 −14q2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq = |
|
|||||||||||||||||||||||||||||||||||
|
(8 +14q |
2 |
) |
2 |
(1 |
+ q |
2 |
|
) |
(8 |
+14q |
2 |
) |
2 |
|
|
|
|
16(8 |
|
+14q |
2 |
) |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
8 −14q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (q |
|
14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
9 ∫ |
8 +14q |
2 + ∫ |
(8 |
|
+ |
14q |
2 |
) |
2 dq |
|
|
= 9 ∫ |
14(( 8) |
2 |
+ |
( 14q) |
2 |
) |
+ ∫d |
|
|
8 |
+14q |
2 |
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14q |
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= |
|
|
|
|
|
arctg |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
8 |
14 |
|
|
|
8 |
|
|
|
8 |
+ |
14q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Возвращаемся |
|
|
|
к |
|
|
|
|
переменной |
|
|
|
|
t |
|
с |
|
|
|
|
восстановлением |
|
|
|
|
пределов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегрирования.
|
2π |
|
dtgt |
|
|
|
|
|
|
1 |
|
|
|
|
|
14tgt |
|
|
tgt |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|||||||||
144 ∫ |
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
= |
9 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
(8 +14tg |
2 |
t) |
2 |
|
|
|
|
|
|
|
|
|
8 |
|
|
8 +14tg |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
8 14 |
|
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgt |
|
|
|
|
|
π |
−0 |
|
|
|
|
|
|
|
|
|
|
tgt |
|
|
|
|
3 |
π −0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
7 |
|
|
|
|
|
|
|
|
1 |
|
|
|
7 |
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= 9 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||
|
4 7 |
|
arctg |
4 |
tgt |
8 |
+14tg |
|
|
|
|
|
|
4 7 |
arctg |
4 |
tgt |
8 +14tg |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
0 |
|
|
|
|
|
|
|
|
|
|
t |
|
π |
+0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
157

|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
tgt |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
+ |
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
tgt |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
− 0 |
+ |
|
|
|
|
− |
− |
|
|
|
|
|
|
+ 0 − |
− |
|
|
|
|
= |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 + |
|
14tg |
|
|
t |
|
|
π |
+0 |
|
|
8 7 |
|
|
|
|
|
|
8 7 |
|
|
|
|
|
8 7 |
|
|
|
|
|
|
|
8 7 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
= 9 |
|
|
4π |
= |
|
|
9π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2π |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−sin t)(11 − 3 cos 2t) − 3 cost sin 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
∫ ydx = ∫ |
|
|
|
|
|
|
|
|
|
sin t |
|
|
18 |
|
|
|
dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
11 |
− 3 cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11 − 3 cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
γ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Повторяем аналогичные действия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
|
|
18sin t |
|
|
|
|
|
|
|
(−sint )(11 −3cos 2t) −3 cost sin 2t |
dt |
=18∫ |
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11 −3cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
(11 −3cos 2t) |
3 |
|
|
|
|
|
|
|
|
|
11 −3 |
1 − q |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
11 |
1 + q |
2 −3 |
|
|
|
|
|
|
|
|
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 + q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + q2 |
|
|
|
|
dq |
|
|
|
|
|
|
|
q(−8q −14q |
3 |
|
− 6q) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=18∫ |
|
|
|
dq |
= |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ q |
2 |
|
|
(8 |
|
+14q |
2 |
) |
2 |
(1 |
+ q |
2 |
) |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 −3 |
1 + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
=18∫ |
|
|
(−14)q2 (1 + q2 ) |
|
|
dq = −18∫ |
14q2 dq |
|
= −18∫ |
14q2 +8 −8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
(8 +14q |
2 |
) |
2 |
(1 + q |
2 |
) |
(8 |
+14q |
2 |
) |
2 |
(8 |
+14q |
2 |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
dq dq dq dq
=−18 ∫8 +14q2 −8∫(8 +14q2 )2 =144∫(8 +14q2 )2 −18∫8 +14q2 =
=• • Воспользуемся решением предыдущего интеграла • • =
= 9∫ |
|
dq |
|
+ 9∫ |
8 −14q2 |
|
dq −18∫ |
dq |
|
= −9∫ |
dq |
|
+ 9∫ |
8 −14q2 |
|
dq. |
||||
8 |
+14q |
2 |
(8 +14q |
2 |
) |
2 |
8 +14q |
2 |
8 +14q |
2 |
(8 +14q |
2 |
) |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Возвращаемся к переменной t, восстанавливаем пределы интегрирования, используем вычисления предыдущего интеграла. Не трудно видеть, что
|
|
|
∫ydx = − |
9π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
2 7 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Итоговый результат циркуляции вектора |
− |
вдоль контура γ : |
||||||||||||||
F |
||||||||||||||||
|
|
|
|
|
|
|
9π |
|
|
|
9π |
|
18π |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ц = ∫Fdl = ∫(2x − y)dx + (x − 2 y)dy + zdz = − |
− |
|
|
|
+ |
|
= |
|
= |
|
7π. |
|||||
|
|
|
|
7 |
||||||||||||
γ |
|
|
γ |
|
|
|
2 7 |
|
2 7 2 7 |
|
|
|||||
158

б)Циркуляция вектора |
− |
||
F с помощью формулы Стокса определяется: |
|||
− − |
|
− |
|
Ц = ∫F dl = ∫∫rotF n ds., где σ - поверхность, натянутая на контур циркуляции.
λσ
Внашем примере на этот контур натянуты обе поверхности σ1 и σ2.
−
Определим циркуляцию вектора F в обоих случаях. Обе поверхности однозначно проектируются на плоскость z = 0 в одну и ту же область,
ограниченную эллипсом r = |
18 |
|
. Поэтому для определения потока |
|||||||||||||||||
11 −3cos 2t |
||||||||||||||||||||
вектора rotF выбираем формулу: ∫∫rotF n ds = ∫∫rotF n dxdy . |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
σ xy |
|
cosγ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
− |
|
|
|
− |
− |
|||||||||
|
|
σ1 : z2 = x2+y2 ; ϕ1 = x2+y2-z2 = 0, |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
n1 = ± 2x i |
+ 2 y j− 2z k . |
|||||||||||||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y2 + 4z2 |
|||||||||
−
Циркуляция вектора F в сторону увеличения параметра t происходит против часовой стрелки, если смотреть на контур циркуляции сверху
−
(рис.3.38).По правилу винта этой циркуляции соответствует вектор n1 ,
направленный во внутреннюю сторону поверхности конуса σ1. Этот вектор составляет с осью Оz острый угол значит и поэтому нужно перед
−
формулой для n1 выбрать знак «-», т.е.
−
i
rotF = ∂ ∂x
2x − y x
n |
|
− |
|
− |
− |
|
− |
− |
− |
= − 2x i |
+ 2 y j− 2z k |
= − 2x i |
− 2 y j+ 2z k |
||||||
− |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4x2 |
+ 4 y2 + 4z 2 |
|
4x2 + 4 y2 + 4z 2 |
|||||
|
|
|
|||||||
−−
j k
∂ |
|
∂ |
=2 к. |
|
|
|
− |
∂y |
|
∂z |
|
− 2y z |
|
||
159
|
|
|
|
|
|
|
|
|
− |
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
− |
|
− |
|
− 2x i |
− 2 y j+ 2z k |
dxdy |
|
|
|
|
|
2z |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫2 |
|
dxdy = |
||||||||||
Ц = ∫∫rotF |
n ds = ∫∫2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
2z |
|
|
|
|
|||||||||||||||
|
σ |
σxy |
|
|
4x |
|
+ 4 y |
|
|
+ |
4z |
|
|
|
|
|
|
σ xy |
|
|
2z |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 + 4 y 2 + 4z 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
2π |
|
18 |
|
|
2π |
|
|
|
|
|
|
|
18 |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
11−3 cos 2t |
|
r |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
π |
|
|
|
|
9 |
|
||||||||
= 2∫∫dxdy = 2 ∫dt |
|
∫rdr = 2 ∫dt |
|
|
|
11−3 cos 2t =18 ∫ |
dt =18 |
|
= |
7π. |
|||||||||||||||||||||||
|
|
|
|
|
1 −3cos 2t |
2 |
7 |
7 |
|||||||||||||||||||||||||
σ xy |
0 |
0 |
|
|
|
0 |
2 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||
Этот интеграл по известной методике определялся ранее.
|
|
σ2 : z = 9-3x2-6y2, ϕ2 = 3x2+6y2+z2-9 = 0, |
|
− |
|
− |
− |
|
|
|
||||||||||||||||
|
|
n2 = ± 6x i |
+12 y j+ |
2z k . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36x2 +144 y2 + 4z2 |
|
|
|
||||
|
|
Для |
|
поверхности |
|
эллипсоида |
|
σ2 |
вектор |
− |
|
|
|
|
|
|||||||||||
|
|
|
|
|
n2 , соответствующий |
|||||||||||||||||||||
циркуляции вектора |
− |
|
направлен во внешнюю сторону поверхности, |
угол |
||||||||||||||||||||||
F , |
||||||||||||||||||||||||||
(n2 , |
|
− |
|
|
cos γ > 0 , знак перед |
− |
|
|
|
|
|
|
|
|
|
|||||||||||
|
O z) - острый, |
n2 - «+». |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
− |
|
− |
|
|
|
dxdy |
|
|
|
|
9 |
|
|
||
|
|
|
|
|
− |
− |
|
|
6x i+12 y j+ |
2z k |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ц = ∫∫rotF |
n ds = ∫∫2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2∫∫dxdy = |
|
|
7π. |
||||||||
|
36x |
2 |
+144 y |
2 |
+ 4z |
2 |
|
2z |
|
7 |
|
|||||||||||||||
|
|
σ |
|
σxy |
|
|
|
|
|
|
|
|
|
|
σ xy |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
36x2 +144 y 2 + 4z 2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3.5.2.5. Задания на контрольную работу.
−
Задание 1. Вычислить поток векторного поля F через кривую поверхность тела V, заданного ограничивающими его поверхностями (нормаль внешняя).
1. |
− |
− |
− |
, |
|
|
|
F = x 2 |
i+ z 2 |
j |
|
|
|
||
2. |
− |
|
− |
+ |
|
− |
|
F = (x |
+ xy 2 ) i |
( y − yx 2 ) j+ |
|||||
3. |
− |
− |
|
− |
− |
, |
|
F = z 2 x i+ x |
2 y j+ y 2 z k |
|
|||||
4. |
− |
|
− |
|
− |
+ |
|
F = (x +y 2 |
) i+ ( y + z 2 ) j |
||||||
V: z 2 =1− x − y , x = 0, y = 0, z = 0.
− − , V: x2 + y2 = z2, z = 1, z = 9.
(z 3) k
V: 4z = y2, 2x – y = 0, x + y = 9, z =0.
−
(z + x2 ) k , V: x + y = 6, y =  3x , z=4y, z = 0.
3x , z=4y, z = 0.
160
5. |
− |
− |
− 2x j |
− |
|
− |
|
|
|
|
V: x = y2 + z2 - 1, x = 3, x = 8. |
|||||||||||
F = 3z i |
−4 y k , |
|
|
|
||||||||||||||||||
6. |
− |
|
2 |
|
− |
3z |
2 |
− |
2 − |
, |
|
|
|
|
|
|
|
|
2 |
|||
F = 2 y |
i+ |
|
j− x |
k |
|
|
V: x + z = 4, x = y , z = 0. |
|||||||||||||||
7. |
− |
|
− |
|
|
2 |
|
− |
|
|
|
− |
|
|
|
|
|
|
|
2 |
y = 3 - x, y = 0,z=0. |
|
F = 4z i |
+ 3x |
|
|
j− 2xyz k , |
|
|
V: z = 1 - x , |
|||||||||||||||
8. |
− |
2 |
− |
|
2 |
− |
, |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
F = y |
|
i+ z |
|
k |
|
|
|
|
|
|
V: y = 1 – x - z, x = 0, y = 0, z = 0. |
|||||||||||
9. |
− |
|
|
|
|
|
− |
|
|
( y − x |
2 |
− |
− |
|
V: y |
2 |
+ z |
2 |
|
2 |
||
F = (x + xy) i+ |
|
) j+ (z −1) k |
|
|
|
= x , x = 1, x = 4. |
||||||||||||||||
10. |
− |
|
2 |
− |
|
|
|
2 |
− |
2 |
− |
, |
V: |
|
2 |
2z – y = 0, z + y = 9, x = 0. |
||||||
F = y |
|
x i+ z |
|
y j+ x |
|
z k |
4x = y , |
|||||||||||||||
Задание 2. Даны векторное поле |
− |
и плоскость p, которое совместно |
||||||||||||||||||||
F |
||||||||||||||||||||||
с координатными плоскостями образует пирамиду V. Пусть σ - основание пирамиды, принадлежащее плоскости p, λ - контур, ограничивающийσ . Вычислить:
−
а) поток векторного поля F через полную поверхность пирамиды (нормаль внешняя) непосредственно;
б) тот же поток с использованием формулы Остроградского;
|
|
|
|
|
|
|
− |
в) циркуляцию вектора F по замкнутому контуру λ непосредственно; |
|||||||
г) ту же циркуляцию – с использованием формулы Стокса. |
|||||||
1. |
|
|
= (3x − 4y + z) |
|
, p = 2x – 3y + z – 2 = 0. |
||
F |
i |
||||||
2. |
|
− |
|
− |
|
||
|
F = (2x +3y −6z) j , p = 2y – 3x - 3z – 3 = 0. |
||||||
3. |
|
− |
|
− |
, p = 2z + 3x – y - 2 = 0. |
||
|
F = (2 y −5x +3z) k |
||||||
4. |
|
− |
|
− |
, p = x – 2y - 3z – 3 = 0. |
||
|
F = (4 y −7x − |
2z) i |
|||||
5. |
|
− |
|
− |
|
||
|
F = (3x +6 y −2z) j , p = y + 3x - 4z – 4 = 0. |
||||||
6. |
|
− |
|
− |
|
||
|
F = (5x −2 y − |
4z) k , p = z - 2y - 3x – 3 = 0. |
|||||
7. |
|
− |
|
|
|
|
|
F = (6z −2 y −3x) j , p = 3x + 2y – z – 2 = 0. |
|||||||
8. |
|
− |
|
|
|
|
|
F = ( y + 2z −3x)i , p = 3y - 2z + 3x – 3 = 0. |
|||||||
161

9. |
− |
− |
F = (3y −2x −3z) k , p = 3z + 2x - 2y – 3 = 0. |
||
−−
10.F = (5x −6 y + z) i , p = 4x - 3y + 4z – 3 = 0.
Задание 3. Поверхность тела образована цилиндрическим параболоидом Р и координатными плоскостями. Найти:
a) Циркуляцию вектора F вдоль контура, образованного пересечением цилиндрического параболоида с координатными плоскостями непосредственно;
b)Ту же циркуляцию – с помощью формулы Стокса;
c)Поток векторного поля F через полную поверхность тела в направлении внешней нормали непосредственно;
d)Тот же поток – с помощью формулы Остроградского.
1. |
|
= (2x − y2 +3z)i + (x − 4 y − 2z 2 ) |
|
+ (x2 − 2 y + z) |
|
|
|
, p : y2 = 4 −4x − z, x = 0, z = 0, y ≥ 0. |
||||||||||||||||
F |
j |
k |
||||||||||||||||||||||
2. |
|
= (z − x + 2 y2 )i + (3y − x + z 2 ) |
|
|
|
|
+ (x2 − y −3z) |
|
, p : x2 = 4x + y + z −4, x = 0, z = 0, y = 0. |
|||||||||||||||
F |
j |
k |
||||||||||||||||||||||
3. |
|
= (4 y2 +3x − z)i + (x + 2 y − z 2 ) |
|
|
|
+ (z − 2x2 −5 y) |
|
|
|
|
, p : z2 = 9 −3x − y, x = 0, z ≥ 0, y = 0. |
|||||||||||||
F |
|
j |
k |
|||||||||||||||||||||
4. |
|
= (x − 2z + y2 )i + (3z2 − 2x + y) |
|
+ (3y − 4z + x2 ) |
|
, p : y2 = x + 4 y + z −4, x = 0, z = 0, y = 0. |
||||||||||||||||||
F |
j |
k |
||||||||||||||||||||||
5. |
|
= (2z − y2 +3x)i + (y − 2z 2 + x) |
|
+ (5z + y − x2 ) |
|
|
|
, p : x2 = 4 − 4 y − z, x ≥ 0, z = 0, y = 0. |
||||||||||||||||
F |
j |
k |
||||||||||||||||||||||
6. |
|
= (y2 − 2x + z)i + (z 2 − y −3x) |
|
+ (y + 2z −2x2 ) |
|
, p : z 2 = 3x + y +6z −9, x = 0, z = 0, y = 0. |
||||||||||||||||||
F |
j |
k |
||||||||||||||||||||||
7.F = (3x − 2 y2 + z)i + (4x − y − z 2 )j + (2x2 − y + z)k, p : y2 = 9 −3x − z, x = 0, z = 0, y ≥ 0.
8.F = (6z + 2y2 − x)i +(2 y − x +2z2 )j +(3z −4 y + x2 )k, p : x2 = 6x +3y + z −9, x = 0, z = 0, y = 0.
9.F = (3y2 −2x − z)i + (4z 2 − 2x + y)j + (y + 2x2 − z)k, p : z2 = 4 − x −4 y, x = 0, z ≥ 0, y = 0.
10. F = (x −3z +2y2 )i +(3y −4x − z2 )j +(2z −3y +2x2 )k, p : y2 =3x +6y + z −9, x = 0, z = 0, y = 0.
−
Задание 4. Даны векторное поле F и две поверхности, образующие пространственное тело V, ограниченное замкнутой поверхностью σ . Вычислить:
162
−
а) поток векторного поля F через полную (замкнутую) поверхность σ тела V (нормаль внешняя) непосредственно;
б) тот же поток – с использованием формулы Остроградского;
−
в) циркуляцию вектора F по замкнутому контуру r, образованного при пересечении данных поверхностей непосредственно;
г) ту же циркуляцию – с использованием формулы Стокса.
1. |
|
|
|
− |
− |
|
− |
− |
|
|
|
|
|
|
F = 6x i− 2 y j− z k , σ: z = 3 - 2(x2 + y2), z2 = x2 + y2 (z ≥ 0). |
||||||||
2. |
− |
|
|
− |
+ ( y |
|
− |
− |
|
|
|
F = (3z + 2 y) i |
+ z) j− x k , σ: x2 + z2 = 2y, y = 2. |
||||||||||
3. |
− |
− |
− |
|
|
− |
|
|
|
|
|
F = y i+ z j+ (2x − |
3y) k , σ: z = 4 - 2(x2 + y2), z = 2(x2 + y2). |
||||||||||
4. |
− |
− |
|
|
− |
|
|
− |
|
|
|
F = x i |
− (2 y − x) j+ (4z − |
2 y) k , σ: x2 + y2 = z, z = 2x. |
|||||||||
5. |
− |
− |
+ |
|
− |
|
− |
|
|
|
|
F = z i |
(2x + 3z) j− y k , σ: x2 + z2 = y2, y = 2. |
||||||||||
6. F = (2z − x) i− (3z + y) j− (x + 2 y) k , σ: y2 = x2 + z2, y2 = 6- 12 (x2 + y2). |
|||||||||||
|
− |
|
|
− |
|
|
− |
|
− |
|
|
7. |
− |
|
− |
|
|
− |
− |
, σ: z = 6 - x2 - y2, z2 = x2 + y2, (z ≥ 0). |
|||
F = 4 y i |
− (2x + 3y) j− z k |
||||||||||
8. |
− |
|
|
− |
|
|
− |
|
− |
||
F = (x |
− 2z) i+ ( y − 2x) j+ (z − |
2 y) k , σ: z2 = x2 + y2, z2 = 18 - (x2 + y2). |
|||||||||
9. |
|
− |
|
|
− |
|
|
− |
− |
||
|
F |
= ( y + 6x) i+ 5(x + z) j− |
4 y k , σ: 3z = 27 - 2(x2 + y2), z2 = x2 + y2, (z > 0). |
||||||||
10. |
− |
|
− |
|
− |
− |
, σ: |
4z = x2 + y2, z = 4. |
|||
F = 2z i− (3x |
− z) j |
− z k |
|||||||||
−
Задание 5. Вычислить циркуляцию вектора F , вдоль контура γ образованного пересечением кругового конуса σ1 и эллипсоида σ2:
а) непосредственно, б) с помощью формулы Стокса.
1. |
− |
|
− |
− |
− |
|
σ1:z2=x2+y2, σ2 :z2=4-x2-3y2. |
F = (x − 2 y) i |
+ (3x + y) j+ 2z k , |
||||||
2. |
− |
− |
|
− |
− |
, |
σ1:x2=y2+z2, σ2 :x2=16-12y2-4z2. |
F = 4x i |
− (2 y |
+ z) j+ (5z |
− y) k |
||||
163
3. |
− |
|
− |
− |
|
− |
|
σ1:y2=x2+z2, σ2 :y2=9-5x2-4z2. |
|
F = (3x |
− z) i+ |
2 y j− (x + 2z) k , |
|
||||||
4. |
− |
|
− |
|
− |
− |
, |
σ1:z2=2x2+2y2, |
σ2 :z2=12-10x2-2y2. |
F = (5x |
+ 2 y) i |
+ (x −3y) j+ 3z k |
|||||||
5. |
− |
− |
|
− |
|
− |
, |
σ1:x2=4z2+4y2, |
σ2 :x2=10-4y2-6z2. |
F = 7x i |
+ (4z −3y) j+ |
(z + 4 y) k |
|||||||
6. |
− |
|
− |
− |
|
− |
, |
σ1:y2=2x2+2z2, |
σ2 :y2=6-x2-5z2. |
F = (2x |
−3z) i−5y j+ |
(3x − z) k |
|||||||
7. |
− |
|
− |
|
− |
− |
|
σ1:z2=4x2+4y2, |
σ2 :z2=16-4x2-12y2. |
F = (3x |
+ y) i+ (2x − y) j− 4z k , |
|
|||||||
8. |
− |
− |
|
− |
|
− |
, |
σ1:x2=2y2+2z2, |
σ2 :x2=12-2y2-10z2. |
F = 2x i |
− (3y − 2z) j+ |
( y + |
3z) k |
||||||
9. |
− |
|
− |
− |
|
− |
, |
σ1:y2=4x2+4z2, |
σ2 :y2=4-3x2-z2. |
F = (x |
+ 3z) i+ |
4 y j− (2x − |
4z) k |
||||||
10. |
− |
|
− |
|
− |
− |
, |
σ1:z2=x2+y2, σ2 :z2=10-4x2-6y2. |
|
F = (2 y |
− x) i− (3x + 4 y) j+ 3z k |
||||||||
164
