e2 |
|
u = ln2 x |
|
du = 2 ln x |
dx |
|
|
|
|
|
|
|
1e |
2 |
|
|
e2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∫ln2 x |
dx = |
|
|
|
|
|
|
= x |
ln2 x |
|
− 2 ∫ln xdx = |
|||||||||||||||
|
|
x |
|
||||||||||||||||||||||||
|
|
dv = dx |
|
v = x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||
|
|
u = ln x |
du = |
dx |
|
|
|
|
|
|
|
e2 |
e2 |
|
|
|
|
|
(e |
|
−1). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
|
|
|
|
= |
4e |
2 |
− 2 |
|
|
− ∫dx |
|
= 2 |
2 |
|||||||||||||
|
x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
dv = dx |
v = x |
|
|
x ln x |
1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
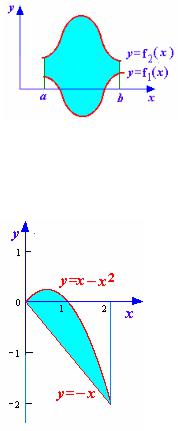
Вычисление площадей плоских фигур
Пусть плоская фигура |
на отрезке [a,b] |
|
ограничена графиками двух функций |
y=f1(x) и |
|
y=f2(x), причем f2(x)≥f1(x) |
(см. рис. |
1.1). Тогда |
|
искомая площадь вычисляется по формуле: |
|
b |
Рис. 1.1 |
S = ∫[ f2 (x) − f1 (x)]dx . |
|
a |
|
Пример. Вычислить площадь фигуры, |
|
ограниченной линиями: y=x–x2, y=–x. |
Решение. Сделаем чертеж (см. рис.1.2). Найдем точки пересечения параболы и прямой:
x − x2 = −x x1 = 0,x2 = 2.
|
|
|
|
Поскольку на отрезке [0;2] x–x2 ≥ –x, то |
|||||
Рис.1.2 |
|
площадь заданной фигуры будет равна |
|||||||
21 |
|
|
|
2 |
|
|
|
4 |
|
S = ∫ |
|
|
2 |
|
− x |
2 |
)dx = |
. |
|
|
|
||||||||
(x − x |
|
) − (−x) dx = ∫(2x |
|
3 |
|||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. Если функция f(x)≤ 0, то определенный интеграл будет меньше нуля. Знак минус означает, что криволинейная трапеция расположена ниже
21
b
оси Оx и ее площадь будет равна S= −∫ f (x)dx .
a
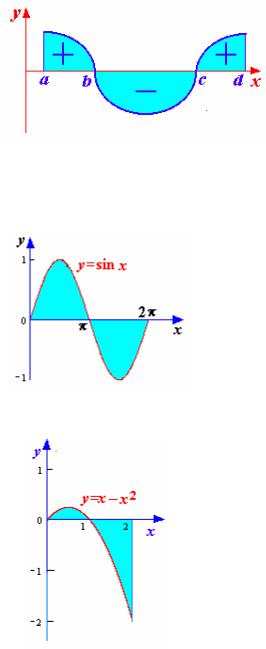
Может оказаться, что функция f(x) на отрезке интегрирования несколько раз меняет знак. В этом случае интеграл нужно разбить на сумму интегралов по участкам, на которых подынтегральная функция имеет постоянный знак. Например, площадь фигуры на рис.1.3 будет иметь вид:
Рис.1.3
Рис.1.4
Рис.1.5
b c d
S= ∫ f ( x ) d x − ∫ f ( x ) d x + ∫ f ( x ) d x
a b c
Пример. Вычислить площадь фигур, ограниченных линиями:
а) y=sinx, y=0, 0≤x≤2π; |
|
б) y=x–x2, y=0, 0≤x≤2. |
|
Решение. а) Сделаем |
чертеж (см. |
рис. 1.4). Так как при 0≤x≤π |
sinx≥0 и при |
π≤x≤2π sinx≤0, то |
|
π2π
S = ∫sin xdx − ∫ sin xdx = 4 (кв. ед.)
0 π
б) Сделаем чертеж (см. рис.1.5). Найдем точки пересечения параболы с осью Ox:
x − x2 = 0 x1 = 0,
x2 = 1.
Из рисунка видно, что
1 2
S = ∫(x − x2 )dx − ∫(x − x2 )dx =1 (кв. ед.)
0 1
22
Заметим, что криволинейная трапеция может образовываться графиком функции также и с осью Oy (см. рис.1.6). Тогда площадь такой криволинейной трапеции можно записать в виде
|
d |
|
S = ∫ϕ( y)dy . |
|
c |
|
Такой случай следует иметь ввиду, поскольку это |
Рис.1.6 |
может сильно сократить вычисления. |
Пример. Вычислить площадь фигуры, ограниченной параболами:
y2=2x и y2=6–x.
Решение. Будем искать площадь данной фигуры относительно оси Oy. Ординаты точек пересечения линий равны y1=–2 и y2=2. Следовательно,
2 |
|
|
y2 |
|
|
S = ∫ |
(6 |
− y2 ) − |
|
dy =16 (кв. ед.) |
|
2 |
|||||
−2 |
|
|
|
||
|
|
|
Рис. 1.7
Параметрические функции
Пусть |
верхняя |
граница |
криволинейной |
трапеции |
задана |
|||
параметрическими функциями: |
x=x(t), y=y(t), t1≤ t ≤t2, причем |
x(t1)=a, |
||||||
x(t2)=b. Поскольку площадь криволинейной |
трапеции |
задается формулой |
||||||
b |
|
|
|
|
|
|
|
|
S= ∫y(x)dx |
(если |
y(x)≥0 |
на |
отрезке |
[a,b]), то, |
производя |
замену |
|
a
23
переменной, получим формулу для вычисления площади криволинейной трапеции, ограниченной кривой, заданной параметрически:
t2
S = ∫y(t) x′(t)dt
t1
Пример.
1.9):
Рис. 1.9
Вычислить площадь фигуры, ограниченной эллипсом ( рис
x = a cost, |
0 ≤ t ≤ 2π . |
|
|
y = bsin t, |
|
Решение. Вычислим площадь верхней половины эллипса, а затем результат удвоим. Здесь x меняется от –a до a, следовательно, t
должно изменяться от π до 0. Таким образом,
0 0
S = 2∫bsin t(−asin t)dt = −2ab∫sin2 tdt =πab .
π π
Пример. Вычислить площадь фигуры, ограниченной осью Ox и
x = a(t − sin t),
одной аркой циклоиды (см. рис. 1.10):
y = a(1 − cost).
Решение. Для получения одной арки циклоиды, достаточно чтобы t изменялось от 0
до 2π. Тогда получим
Рис. 1.10 |
2π |
S = |
∫ a(1 − cost)a(1 − cost)dt = |
|
0 |
2π
= a2 ∫ (1 − 2cost + cos2 t)dt = 3πa2
0
Полярная система координат
Пусть кривая задана в полярных координатах уравнением: ρ=ρ(ϕ),
24
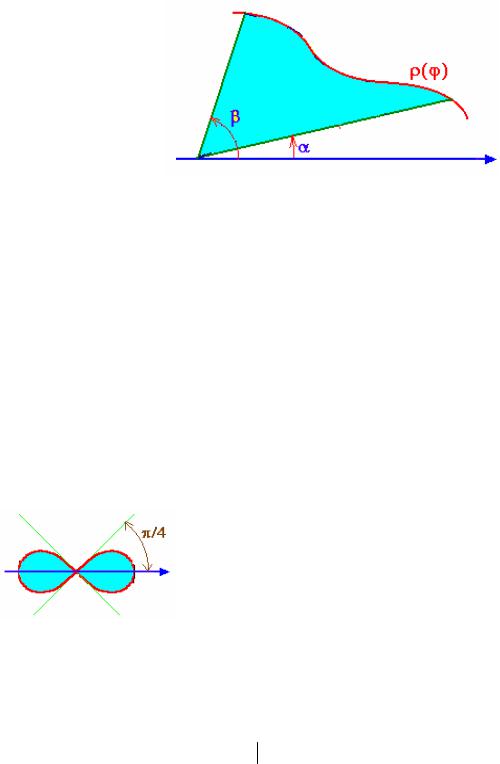
α≤ϕ≤β, причем функция ρ(ϕ) непрерывна и неотрицательна на отрезке [α,β].
Плоскую фигуру, ограниченную кривой ρ(ϕ) и двумя лучами,
составляющими с полярной осью углы α и β, будем называть
криволинейным сектором (рис. 1.11).
Рис. 1.11
Площадь криволинейного сектора вычисляется по формуле:
β
S = 1 ∫ρ2dϕ . (1.2)
2 α
Пример. Вычислить площадь ограниченной: а) лемнискатой Бернулли
ρ2=a2cos2ϕ ; б) трехлепестковой розой ρ=acos3ϕ.
Решение. а) Поскольку ρ2≥0, то cos2ϕ≥0. Отсюда получаем
− |
π |
+ 2πk ≤ 2ϕ ≤ |
π + 2πk −π +πk ≤ϕ ≤ π +πk , |
||
|
2 |
|
2 |
4 |
4 |
|
|
|
где |
k Z. Таким образом, данная кривая |
|
|
|
расположена в двух секторах (см. рис. 1.12). Для |
|||
|
|
нахождения |
искомой |
площади достаточно |
|
|
|
вычислить четверть площади, а затем умножить ее |
|||
Рис. 1.12 |
на 4. Воспользуемся формулой (1.2): |
||||
|
|
|
|
||
|
|
S = 4 1 |
π / 4 |
π / 4 |
|
|
|
∫ ρ2d ϕ = 2 a2 ∫ cos 2ϕd ϕ = |
|||
|
|
2 |
0 |
0 |
|
|
|
|
|
||
= 2a2 21 sin 2ϕ π0 
4 = a2 (sin π2 − sin0) = a2 .
25