Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский институт железнодорожного транспорта, филиал ИрГУПС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

практикум математика часть 2.pdf

Скачиваний:

107

Добавлен:

15.02.2015

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

y				D2
				D2
		x)
	(
	2
	y
		D1		y3(x)
		D1
			x)		D3
			x)
		y	1(
		y
a			b	c	d	x

		b	y2 ( x)
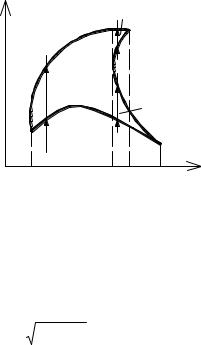
∫∫= ∫∫+ ∫∫+ ∫∫= ∫dx			∫ f (x, y)dy +
D	D1 D2 D3	a	y1 ( x)
c	y2 ( x)	d	y3 ( x)
∫dx	∫ f (x, y)dy + ∫dx ∫ f (x, y)dy
b	y3 ( x)	b	y1 ( x)

Рис. 3.2

Пусть область D построена в полярной системе координат. Напомним связь прямоугольных и полярных координат: x = rcosϕ , y = rsinϕ ,

r = x2 + y 2 , ϕ = arctg	y	, где r – полярный радиус, ϕ - полярный угол,
r = x2 + y 2 , ϕ = arctg	x	, где r – полярный радиус, ϕ - полярный угол,
	x
0 ≤ ϕ ≤ 2π , 0 ≤ r ≤ ∞ .

В двойном интеграле произойдёт замена переменных интегрирования x, y на новые переменные ϕ , r по известным формулам: x = rcosϕ , y = rsinϕ ,

при этом dxdy = rdrdϕ (доказательство не приводим).

В некоторых случаях такая замена переменных упрощает подынтегральную функцию, аналитическое выражение области интегрирования, что приводит к облегчению расстановки пределов и, самое главное, упрощает вычисление самого интеграла.

Правила вычисления двойного интеграла в полярной системе координат

1.Вычисление внутреннего интеграла.

• Внутренний интеграл однозначно берётся по переменной r, при этом область D, должна быть правильной (выпуклой), т.е. полярный радиус проведённый через любую внутреннюю точку области D пересекает её не более в двух точках. Если область D окажется неправильной, то с помощью дополнительных полярных радиусов разбить область D на правильные части

D1, D2, ..., Dn , вычислить интеграл по этим частям и сложить согласно свойству 3.

• Пределами интегрирования внутреннего интеграла являются функции r(ϕ ). Нижний предел – функция r1(ϕ ) , график которой есть граница области D при вхождении в эту область возрастающего полярного радиуса (в частном случае это ноль, если точка (0; 0) входит в область D). Верхний предел – функция r2(ϕ ), график которой есть граница области D при выходе указанного полярного радиуса из области D.

•Нижний и верхний пределы интегрирования – функции – должны быть заданы одним аналитическим выражением (границы области D должны быть гладкими). Если это правило не соблюдается, разбить область D полярными радиусами на части D1, D2, ..., Dn , удовлетворяющие этому правилу и произвести расчёт интеграла по свойству 3.

•Вычисление внутреннего интеграла произвести аналогично такому же пункту вычисления в прямоугольной системе координат.

2.Вычисление внешнего интеграла.

Это обычный определённый интеграл по переменной ϕ , пределы которого ϕ1 - нижний, ϕ2 - верхний есть полярные углы между которыми заключена область D.

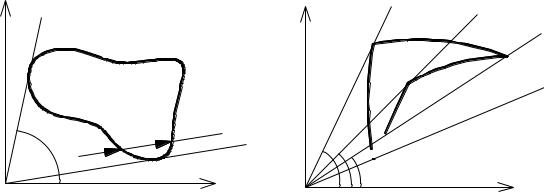
На рис. 3.3. представлены варианты расчёта двойного интеграла в полярной системе координат согласно приведённым правилам.

y			y
			y
	r	2(	ϕ)
	r

ϕ2	r	1(	ϕ)

ϕ1

		D2
	)
	ϕ	r
	(	r
	1	D1
	r	D1
	r

ϕ4 ϕ3ϕ2

ϕ1

r		3	(	ϕ)
r		3	(
						D3
							)
						ϕ
				r	(
		)			4
	ϕ
(2

∫∫ f (x, y)dxdy = ∫∫ f (r cosϕ, r sin ϕ)rdrdϕ =

D D

ϕ2	r2	(ϕ)
= ∫dϕ		∫F(r,ϕ)

ϕ1 r1 (ϕ)

r2(ϕ

ϕ3

ϕ2

rdr

)	r
	1(
		ϕ)
	D2

ϕ1

			ϕ3	r2	(ϕ)
∫∫= ∫∫+ ∫∫+ ∫∫= ∫dϕ					∫F(r,ϕ)rdr +
D	D1	D2	D3 ϕ1	r1 (ϕ)
ϕ4	r3	(ϕ)	ϕ3		r3	(ϕ)
+ ∫dϕ		∫F(r,ϕ)rdr + ∫dϕ				∫F (r,ϕ)rdr
ϕ3	r1 (ϕ)		ϕ2		r4 (ϕ)

∫∫= ∫∫+ ∫∫=

D D1		D2
ϕ2	r1	( ϕ )	ϕ3	r2	( ϕ )
= ∫dϕ		∫F( r,ϕ )rdr + ∫dϕ			∫F( r,ϕ )rdr
ϕ1		0	ϕ2		0

Рис. 3.3

3.2..3. Некоторые приложения двойных интегралов

Эти приложения основаны на геометрическом и физическом смыслах двойного интеграла.

Двойной интеграл применяется для вычисления следующих величин.

1.Вычисление объёма V тела (см. геометрический смысл).

V = ∫∫ f (x, y)dxdy

2.Вычисление площади S плоской фигуры D.

S = ∫∫dxdy ; S = ∫∫rdrdϕ (полярная система).

3.Вычисление массы m плоского тела (пластинки) с поверхностной

плотностью распределения массы f(x, y).

m = ∫∫ f (x, y)dxdy .

4.Вычисление координат (хс, ус) центра массы m плоского тела D.

xc =	My	=	∫∫xf (x, y)dxdy	; yc =	Mx	=	∫∫yf (x, y)dxdy	,
			D				D
	m		m		m		m

где Мх , Му – статические моменты пластинки относительно осей Ох и Оу.

5.Вычисление моментов инерции Ix, Iy, Io относительно осей Ох, Оу

иначала координат плоского тела D.

Ix = ∫∫y2 f (x, y)dxdy ;	Iy = ∫∫x2 f (x, y)dxdy ; Io = Ix + Iy = ∫∫(x2 + y 2 ) f (x, y)dxdy .
D	D

3.2.4. Типовые примеры решения двойных интегралов

Напомним, что для расчёта любых примеров и задач на двойные интегралы нужно обязательно построить область интегрирования D, а затем руководствоваться правилами расчёта.

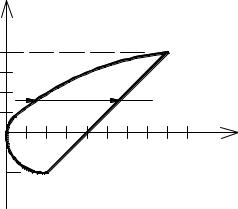
Пример1.Составить двукратный интеграл от функции f(x,y) по областиD, если f(x, y) задана в области D, ограниченной кривыми y2 = 2x ; x – y – 4 = 0.

y
4		y2= 2x						B(8,4)
4
3					D
3
2
1					x-y-4 = 0
					x-y-4 = 0
	1	2	3	4	5	6	7	8	9
−2	A(2,-2)
				Рис. 3.4

Решение. Область D (рис. 3.4) правильная в направлении переменной х, значит внутренний интеграл берётся по х, внешний по у. Стрелка возрастания

xпеременной х при вхождении в область D встречается на границе области D с кривой

х =	у2	(нижний предел интегрирования
	2

внутреннего интеграла) и при выходе из области D встречается с прямой х = =у + 4 (верхний предел).

Проектируем область D на ось Оу. Границы проекции есть числа -2 (нижний предел интегрирования внешнего интеграла), 4 (верхний предел).

Напомним, точки А и В пересечения кривых находятся в результате решения системы уравнений этих кривых.

y+4

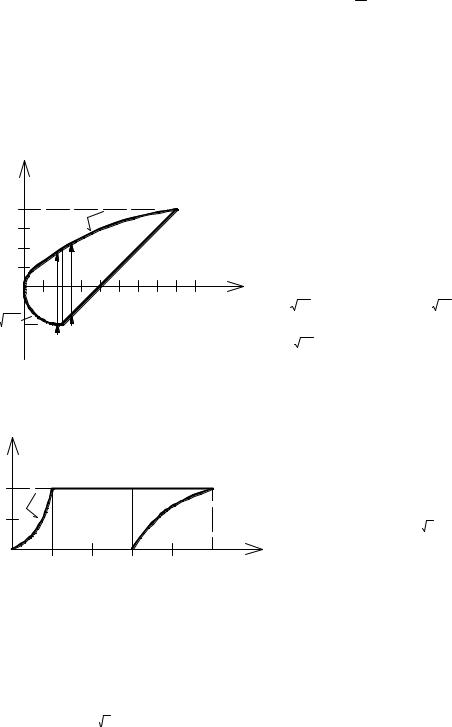
Составляем интеграл: ∫∫ f (x, y)dxdy = ∫dy ∫ f (x, y)dx .

−2

Пример 2.

В условиях примера 1 изменить порядок интегрирования.

Решение. Область D (рис. 3.5) в направлении переменной у правильная,

но нарушено правило задания нижнего предела интегрирования внутреннего

интеграла одним аналитическим выражением (в точке A излом). Разбиваем

область D на две части D1 и D2 составляем

B(8,4)

сумму

двух

интегралов

по

известному

правилу:

-4

f (x, y)dxdy +

f (x, y)dxdy =

∫∫

f ( x, y )dxdy =

∫∫

2 x

y = - 2x

A(2,-2)

∫dx

∫

f (x, y)dy + ∫dx ∫ f (x, y)dxdy.

−

2 x

x−4

Рис. 3.5

Пример

Изменить

порядок

интегрирования

e y +2

0.5

y 2

∫

f (x, y)dx.

3 y

e+2

Рис. 3.6

Решение. По условиям примера

строим область D (рис. 3.6), разбиваем её на 3 части D1, D2, D3 и составляем

интеграл:

1	e y +2		1	x3	3	1	e+2		1
∫dy	∫	f (x, y)dx = ∫dx ∫ f (x, y)dy + ∫dx∫ f (x, y)dy + ∫						dx	∫ f (x, y)dy .
0	3 y		0	0	1	0	3		ln( x−2)

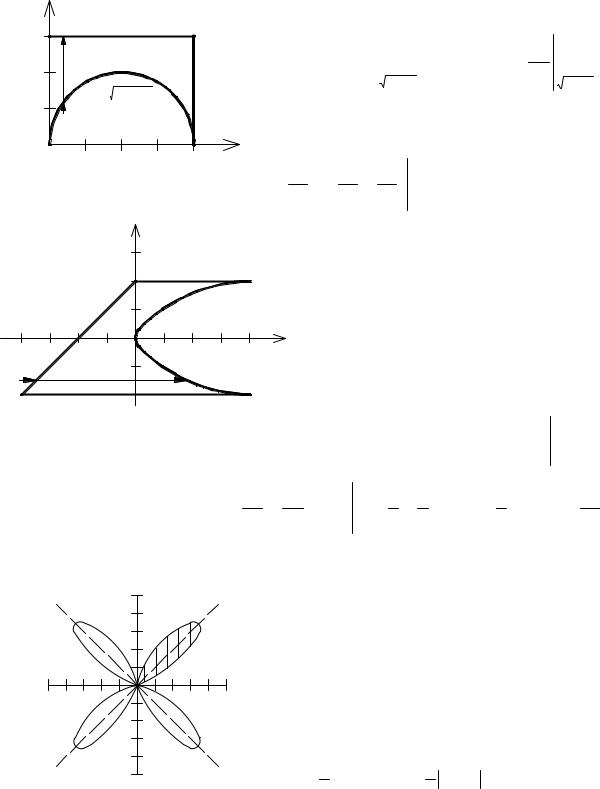
Пример 4. Вычислить∫∫x2 ydxdy ,D: x2 + y2 = 4x , x = 0 , x = 4 , y = 3 , y≥0

																Решение. Область D (рис. 3.7) правильная в
	y					y = 3				направлении у.
	3					y = 3																													3
	3				D														4				3					4			y	2
																			4				3					4				2
	2							4			∫∫x2 ydxdy = ∫dx												∫	x2 ydy = ∫dxx2												=
		y		= 4x-x			2	x =			D								0			4 x−x2						0			2				4 x−x2
							2
	1											4					9 − 4x − x					2			4	9x	2	− 4x		3	+ x		4
	1										=	4										2			4		2			3			4		dx =
											=	∫	x2										dx =		∫										dx =
												∫					2			2					∫				2
		1			2		3	4	x			0					2			2					0				2
		1			2		3	4	x		1				x3			x4			x5			4	1									1024
											1				x3		− 4	x4		+	x5			4	1		64		− 256 +					1024
												9					− 4			+				=		3	64		− 256 +							= 70,4.
				Рис. 3.7							2					3		4			5				2										5
				Рис. 3.7							2					3		4			5		0		2										5
						y
						3											Пример 5. Вычислить площадь фигуры,
								y = 2									Пример 5. Вычислить площадь фигуры,
						2		y = 2									ограниченной линиями y = −2,
						2																													y = x + 2,
			x+2				2	x																											y = x + 2,
							2	x
						1	=
		=			D	1	y																		y = 2, y 2				= x.


		y
−4	−3	−2		−1			1	2	3	4			x					Решение.								Область						D			(рис.3.8)
					−1													Решение.								Область						D			(рис.3.8)
					−2		y = -2									правильная в направлении x.
																правильная в направлении x.

							Рис. 3.8																		2	y2			2					y2
							Рис. 3.8											S = ∫∫dxdy = ∫dy ∫dx = ∫dy x																	=
																		S = ∫∫dxdy = ∫dy ∫dx = ∫dy x																	=
																					D				−2	y−2			−2				y−2
		=		2							3			y		2				2	= 8 − 4 + 2 2 + 8 + 2 + 4 = 40 кв.ед.
		=		∫	(y2 − y + 2)dy = y						−			y			+ 2 y				= 8 − 4 + 2 2 + 8 + 2 + 4 = 40 кв.ед.
				∫						3					2							3 2						3							3
				−2						3					2			−2				3 2						3							3
		Пример					6.	Вычислить								площадь						фигуры,					ограниченной									кривой
										(x2 + y2 )3 = a2 x2 y2 , a > 0.
							S1								Решение.								Переходим								к				полярным
							S1		координатам:										x = r cosϕ, y = r sin ϕ.
															Тогда: (r 2 cos2 ϕ + r 2 sin 2 ϕ)3 = a2 r 2 cos2 ϕ r 2 sin 2 ϕ,
															r 6		= a2 r 4 cos2 ϕ sin 2 ϕ,
					Рис. 3.9										r 2		= 1 a2 sin 2				2ϕ, r = a				sin 2ϕ .
					Рис. 3.9												4							2
		Строим область D (рис. 3.9) в координатах r, φ и вычисляем двойной

интеграл согласно правил его расчета в полярных координатах.

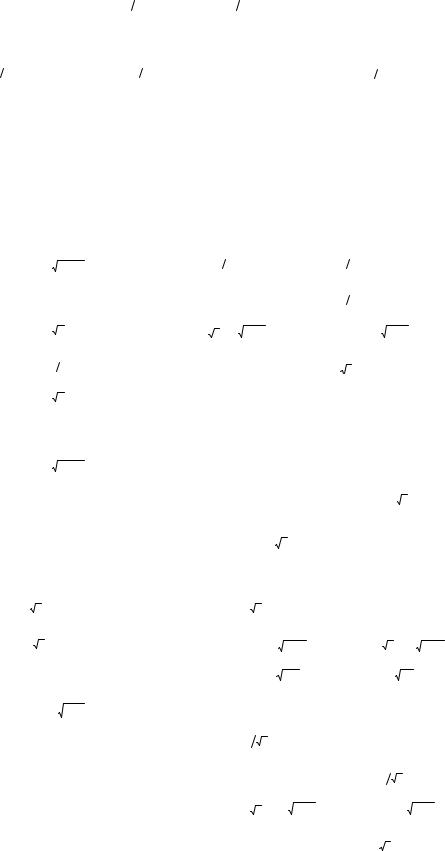
					π 2				a	sin 2ϕ	π 2		r 2			a	sin 2ϕ
									a

S = 4S1 = 4∫∫rdrdϕ = 4 ∫dϕ									2 ∫rdr =4 ∫dϕ							2				=
																2

		D				0			0		0			2				0
π 2	a2		2		a2		π 2	1 − cos 4ϕ				a2						1			π 2		1		2
π 2	a2		2		a2		π 2	1 − cos 4ϕ				a2						1			π 2		1		2
= 2 ∫		sin		2ϕdϕ =			∫				dϕ =				ϕ −				sin 4ϕ			=		πa		.
= 2 ∫	4	sin		2ϕdϕ =	2		∫		2		dϕ =	4			ϕ −			4	sin 4ϕ			=	8	πa		.
0	4				2	0			2			4						4			0		8

3.2.5.Задания на контрольную работу

Задание 1. Изменить порядок интегрирования.

3	25−x2
1а. ∫dx		∫ f (x, y)dy .
0	0
2а. ∫1 dx ∫x f (x, y)dy .
0	x 3
3а. ∫4 dx ∫x f (x, y)dy .
1	0
4	25−x2
4а. ∫dx ∫ f (x, y)dy .
0		3	x
0	4		x
	4
1	1−y2
5а. ∫dy ∫ f (x, y)dx .
−2	y−1
2		4−x2
6а. ∫ dx ∫ f (x, y)dy .
− 2			x2
1	y−1
7а. ∫dy		∫ f (x, y)dx .
0	− 1−y2
0	−x2
8а. ∫dx	∫ f (x, y)dy .
−1	x2 −2
1	2−x2
9а. ∫dx	∫ f (x, y)dy .
0	x2

π 4

sin x

π 2

cos x

1б.. ∫ dx

∫

f (x, y)dy +

∫

dx ∫

f (x, y)dy

π 4

−

−x2

2−

4−x2

2б. ∫

∫ f (x, y)dy + ∫ dx

∫ f (x, y)dy .

−2

−

3б. ∫1 dx ∫1

f (x, y)dy + ∫e dx ∫1

f (x, y)dy .

1−x2

ln x

4б. −∫1dx ∫0

f (x, y)dy + ∫0 dx ∫0

f (x, y)dy .

−2

−2−x

−1

5б. ∫1 dy ∫ f (x, y)dx + ∫e dy ∫1

f (x, y)dx .

ln y

6б. ∫3 dx ∫0

f (x, y)dy + ∫2 dx ∫0

f (x, y)dy .

4−x2 −2

− 4−x2

2+y

− y

7б. −∫1dy ∫ f (x, y)dx + ∫0 dy ∫ f (x, y)dx .

−2

−1

2 arcsin y

arccos y

8б. ∫ dy ∫ f (x, y)dx + ∫ dy ∫ f (x, y)dx.

2− 4−x2

4−x2

9б. ∫dx

∫

f (x, y)dy + ∫dx

∫ f (x, y)dy .

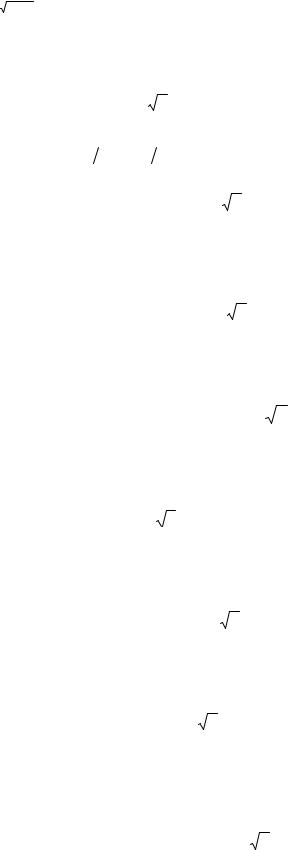
10а. ∫4 dx ∫2 f (x, y)dy .	10б. ∫1	3
10а. ∫4 dx ∫2 f (x, y)dy .	10б. ∫1	dxx∫ f (x, y)dy + ∫2 dx2∫−x f (x, y)dy .
0 4 x−x2	0	0	1 0
Задание 2. Вычислить.
1. ∫∫(8xy +9x2 y2 )dxdy; D : x =1, y = 3	x, y = −x3 .
D
∫∫12 y sin 2xydxdy; D : y = π 4, y = π 2, x = 2, x = 3.
D
2. ∫∫(12xy + 27x2 y2 )dxdy; D : x =1, y = x2 , y = −3 x			(x ≥ 0).
D

∫∫ye−xy8dxdy; D : x = 0, x =1, y = ln 2, y = ln 3.

	4		9		2		2		3
3. ∫∫		xy +		x		y		dxdy; D : x =1, y = x		, y = − x.
3. ∫∫	5	xy +	11	x		y		dxdy; D : x =1, y = x		, y = − x.
D	5		11

∫∫y cos xydxdy; D : x = 0, x = 2, y =π, y = 5π.

4.	∫∫(24xy − 48x3 y3 )dxdy; D : x =1, y = x2 , y = − x.
	D
∫∫4 y sin 2xydxdy; D : x = 0, x =1, y = 2π, y = 3π.
D
5.	∫∫(4xy +16x3 y3 )dxdy; D : x =1, y = 3 x, y = −x3 .
	D
∫∫3y cos xydxdy; D : x = 0, x = 0,5, y =π, y = 2π.
D
6.	∫∫(44xy +16x3 y3 )dxdy; D : x =1, y = x2 , y = −3 x.
	D

∫∫ye−xy2 dxdy; D : x = 0, x = 2, y = ln 3, y = ln 4.

∫∫(xy − 4x3 y3 )dxdy; D : x =1, y = x3 , y = −

∫∫y cos 2xydxdy; D : x = 0, x =1, y =

, y = 2π.

∫∫ 6x

dxdy; D : x =1, y = x

, y = − x.

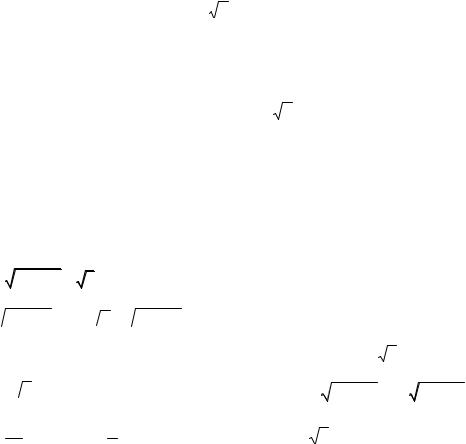
∫∫3ysin		xy	dxdy; D : x = 0, x =1y =				4π	, y =	2π	.
∫∫3ysin			dxdy; D : x = 0, x =1y =				3	, y =	3	.
D	2						3		3
				50
9. ∫∫	3x2 y2 +				x4 y4	dxdy; D : x =1, y = 3 x, y			= −x3 .
9. ∫∫	3x2 y2 +			3	x4 y4	dxdy; D : x =1, y = 3 x, y			= −x3 .
D				3

∫∫ye−xy2 dxdy; D : x = 0, x =1, y = ln 3, y = ln 5.

10. ∫∫(54x2 y2 +150x4 y4 )dxdy; D : x =1, y = x2 , y = −3 x (x ≥ 0).

∫∫y cos xydxdy; D : x = 0, x =1, y =π, y = 2π.

Задание 3. Найти площадь фигуры,

1. y = 24 − x2 , 2 3y = x2 , x ≥ 0.

3 y = 18 − x2 , y = 3 2 − 18 − x2 . .

5. y = 2 x, y = 5ex , y = 2, y = 5.

7. y = 3 x, y = 3 x , x = 4. 9. y = 254 − x2 , y = x − 52 .

ограниченной линиями.

2.	y = 20 − x2 , y = −8x.
4.	y = 32 − x2 , y = −4x.
6.	x2 + y 2 = 36, 3 2 y = x2 (y ≥ 0).
8.	y = 6 − 36 − x2 , y = 36 − x2 , x ≥ 0.

10. y = x, y = 1x , x =16.

Задание 4. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (a > 0).

1.	x6	= a2 (x4 − y4 ).	2.	(x2 + y2 )2 = ax3 .
3.	x4	= a2 (x2 −3y2 ).	4.	x4 = a2 (x2 − y2 ).
5.	y6 = a2 (y4 − x4 ).		6.	(x2	+ y 2 )2 = a2 (x2 + 4 y 2 ).
7.	(x2 + y 2 )2 = a2 (2x2 + 3y2 ).		8.	(x2	+ y 2 )3 = a2 x4 .
9.	y6	= a2 (3y2 − x2 ) (y2 + x2 ).	10. (x2 + y 2 )2 = a2 (3x2 + y 2 ).

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2712 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.11.20183.81 Mб187Подвижной состав. Исправленное.doc
#
30.12.201984.44 Mб1Пособие 80Р.doc
#
12.11.2019176.64 Кб14пособие для поведния семинрских знятий.doc
#
15.02.201530.97 Mб33пособие проводнику.docx
#
15.02.201523.98 Кб26почтовобагажный вагон.docx
#
15.02.20153.83 Mб107практикум математика часть 2.pdf
#
15.02.20154.76 Mб123практикум по математике часть 3.pdf
#
15.02.2015328.84 Кб49Практич_МТТ_с_приложением_МТТ.pdf
#
15.02.2015439.81 Кб35Практическое занятие.doc
#
18.09.201934.46 Кб6Предпринимательство.docx
#
15.02.201530.21 Кб14прием док-в в общ-е (1).doc