3.3. Тройной интеграл

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский институт железнодорожного транспорта, филиал ИрГУПС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

практикум математика часть 2.pdf

Скачиваний:

107

Добавлен:

15.02.2015

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2713 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

		3.3. Тройной интеграл
z
zi		3.3.1. Определение
		3.3.1. Определение
V	V i
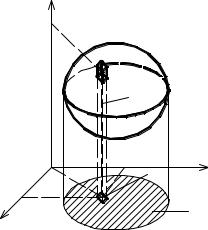
V	f(x i, yi)	Тройным интегралом от функции f(x,y,z) по
		области V называется предел интегральной
	yi	суммы
	Si	y	n
xi			n
xi	D	n→∞lim	∑ f (xi , yi , zi )	Vi = ∫ f (x, y, z)dV =
x	D	n→∞lim	∑ f (xi , yi , zi )	Vi = ∫ f (x, y, z)dV =
x		diam V →0 i=1		V
		i
Рис. 3.10		= ∫∫∫ f (x, y, z)dxdydz,
		V

где f(x,y,z) – непрерывная функция в объёмной области V,

Vi – объём i-го малого элемента, на которые разбита область V, (i=1,n), см рис.3.10,

n – количество малых элементов,

xi, yi, zi – координаты точки принадлежащей области Vi: (xi , yi , zi)

Vi ,

f(xi , yi , zi) – значение функции в точке (xi , yi , zi).

Если f(x, y, z) – объёмная плотность распределения вещества	кг	в
	3
м

области V (в объёме V) , то f(xi , yi , zi) Vi – масса элементарного куска вещества объёмом Vi , интегральная сумма – приближённое значение, а её предел – точное значение массы вещества в объёме V.

Физический смысл тройного интеграла – это есть масса вещества, заключённой в объёме V.

3.3.2. Вычисление тройного интеграла

Тройной интеграл вычисляется через трёхкратный :

∫∫∫ f (x, y, z)dxdydz = ∫{∫[∫ f (x, y, z)dz]dy}dx =∫{∫[∫ f (x, y, z)dy]dz}dx =...

V V V

Сначала вычисляется внутренний, затем средний и, наконец, внешний интеграл. Переменные интегрирования в этих трёх интегралах – разные. Существует шесть вариантов расчета с различным порядком интегрирования (dzdydx; dydzdx; dzdxdy;…). Результат вычисления один и тот же, но эффективность расчёта (простота) может быть разной.

Для вычисления тройного интеграла нужно обязательно построить рисунок области интегрирования V, без которого немыслимо сформировать расчётный интеграл.

Пусть область V построена в прямоугольной системе координат. Определение. Область V называется правильной (выпуклой) в

направлении переменной интегрирования, если прямая, проходящая через любую внутреннюю точку области V параллельно оси переменной интегрирования, пересекает границы области V не более чем в двух точках.

Правила вычисления тройного интеграла в прямоугольной системе координат

1.Вычисление внутреннего интеграла

•Внутренний интеграл вычисляется по той переменной, для которой область V правильная. Если это правило нельзя выполнить, разбивают область V поверхностями (проще плоскостями) на части V1, V2,..., Vn, которые будут правильными в направлении выбранной переменной интегрирования и дальнейший расчёт производится согласно свойству3.

•Пределами интегрирования внутреннего интеграла являются функции выбранной переменной интегрирования в зависимости от оставшихся двух переменных (уравнения поверхностей). Нижний предел –

функция, описывающая поверхность, которая есть граница области V при вхождении в эту область стрелки, указывающей направление возрастания выбранной переменной интегрирования. Верхний предел – функция, описывающая поверхность, которая является границей области V при выходе указанной стрелки из области V.

•Нижний и верхний пределы интегрирования – функции – должны быть заданы одним аналитическим выражением (границы – поверхности области V должны быть гладкими). Если эти границы кусочно-гладкие, разбить область V поверхностями на части V1,V2,...,Vn,удовлетворяющие этому правилу и далее вычислять согласно свойству 3.

•Вычисление внутреннего интеграла производить по известным правилам расчёта определённого интеграла, при этом две переменные, не участвующие в интегрировании считать постоянными величинами.

Результатом расчёта внутреннего интеграла является функция двух переменных, не участвующих в интегрировании.

2.Вычисление среднего и внешнего интегралов.

Это вычисление производить по правилам расчёта двойного интеграла, при этом область интегрирования D есть проекция области V на координатную плоскость оставшихся двух переменных.

Результат расчёта тройного интеграла – число (масса тела).

На рис. 3.11 приводятся различные варианты расчёта тройного интеграла в прямоугольной системе координат.

z	Z2	(x, y)

Z1(x, y)

y1(x)

y2(x)

y2 ( x)

( x, y)

∫∫∫f (x, y, z)dxdydz = ∫dx ∫dy

∫ f (x, y, z)dz.

y1 ( x)

z1 ( x, y)

	b
D	y1(x, z)		V
	x1(z)			y2	(x, z)
x2(z)	a
x2(z)
					y
	x
	b	x2 ( z)	y2 ( x,z )
∫∫∫f (x, y, z)dxdydz = ∫dz		∫dx	∫ f (x, y, z)dy.
V	a	x1 ( z)	y1 ( x,z)

Рис. 3.11

Цилиндрическая система координат есть сочетание полярных координат в любой координатной плоскости трёхмерной прямоугольной системы и оставшейся прямоугольной координаты.

Варианты координат цилиндрической системы: (r,ϕ ,z), (r, ϕ ,x), (r, ϕ ,y).

В некоторых случаях тройной интеграл в этой системе вычисляется значительно проще, чем в прямоугольной системе.

Правило вычисления тройного интеграла в цилиндрической системе координат

Средний и внешний интегралы образуют двойной интеграл в полярной системе координат, а внутренний интеграл вычисляется в прямоугольной системе по оставшейся переменной с использованием известных правил.

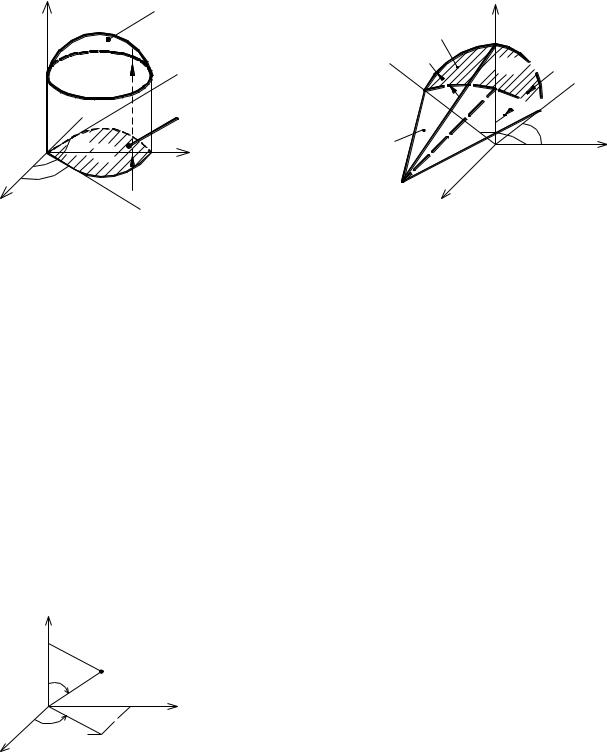
На рис. 3.12 показаны некоторые варианты расчёта тройного интеграла в цилиндрической системе координат.

z(r,ϕ)

	V				z = 0
	ϕ2	D		)	y
				ϕ
			(
x	ϕ1		r
x	ϕ1

x = 0

x(r,ϕ)

	r
	(
	2	ϕ
	2	)
		)

V r1(ϕ)

ϕ2 ϕ1

r (ϕ)

(r ,ϕ)

∫∫∫F (r,ϕ, x)rdrdϕdx =

∫∫∫F(r,ϕ, z)rdrdϕdz = ∫dϕ ∫ rdr

∫F (r,ϕ, z)dz

ϕ1

ϕ2

(ϕ)

x(r ,ϕ)

∫dϕ

∫

rdr ∫F(r,ϕ, x

Рис.12

ϕ1

r1 (ϕ)

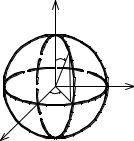
В сферических координатах положение точки Р в трёх мерном

пространстве определяется тремя числами θ, r,ϕ (рис. 3.13), где

r – расстояние от начала координат до точки – это радиус-вектор точки,

θ –

угол между осью Оz

и радиус-вектором,

угол между осью Ох и

проекцией радиус-вектора на плоскость хOу.

Положительные направления углов показаны на рис. 3.13. 0 ≤ r < ∞ ,

0≤θ ≤π , 0≤ϕ ≤2π .

Связь прямоугольных и сферических координат:

x = rsinθ cosϕ , y = rsinθ sinϕ , z = rcosθ .

Тройной интеграл в сферических координатах

P(θ, r, ϕ)

θ r

(применяется достаточно редко) имеет вид:

I= ∫∫∫F(θ, r,ϕ)r 2 sinθdrdϕdθ .

Преобразование

тройного интеграла от

Рис. 3.13

декартовых координат к сферическим имеет вид:

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f [r sinθ cosϕ, r sinθ sinϕ, r cosθ]r 2 sinθdrdϕdθ.

	V		V
	z		Если область V представляет собой шар -
	z
			x2 + y 2 + z 2		≤ R2 (рис. 3.14), то
V	θ		∫∫∫ f (x, y, z)dxdydz =
V			∫∫∫ f (x, y, z)dxdydz =
		y	V
	ϕ	y		2∫πdϕπ∫sinθdθ∫R
x			=	2∫πdϕπ∫sinθdθ∫R		f [r sinθ cosϕ, r sinθ sinϕ, r cosθ]r 2 dr.
x	Рис. 3.14			0 0	0
	Рис. 3.14

3.3.3. Некоторые приложения тройных интегралов

Тройной интеграл применяется для вычисления следующих величин.

1.Вычисление объема тела (f (x, y, z)=1)

V = ∫∫∫dxdydz = ∫∫∫rdrdϕdz = ∫∫∫r 2 sinθdrdϕdθ.

V V V

2. Вычисление массы тела объемом V с объемной плотностью распределения массы f(x,y,z).

m = ∫∫∫ f (x, y, z)dxdydz

3.Вычисление координат центра масс xc , yc , zc тела массой m.

xc =	∫∫∫xf (x, y, z)dV	, yс =	∫∫∫yf (x, y, z)dV	, zc =	∫∫∫zf (x, y, z)dV	.
	V		V		V
	m		m		m

4. Вычисление моментов инерции Ix, Iy, Iz, I0 тела относительно осей Ox, Oy, Oz и начла координат.

I x = ∫∫∫(y 2	+ z 2 )f (x, y, z)dV ,	I y	= ∫∫∫(x2	+ z 2 )f (x, y, z)dV ,
V			V
I z = ∫∫∫(x2	+ y 2 )f (x, y, z)dV ,	I0	= ∫∫∫(x2	+ y 2 + z 2 )f (x, y, z)dV .
V			V

3.3.4. Типовые примеры решения тройных интегралов

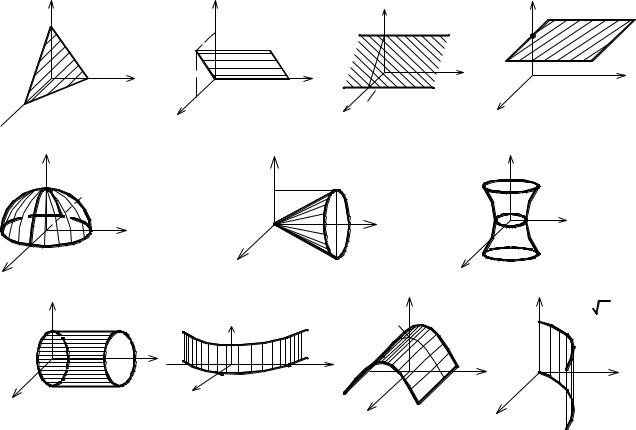
Напомним, что здесь, как и в двойном интеграле, важным является построение чертежа области интегрирования. Область V ограничивается замкнутой поверхностью, которая в свою очередь состоит из отдельных кусков гладких поверхностей, заданных своими уравнениями. На рис. 3.15 представлены некоторые уравнения поверхностей и их геометрическое изображение, которые помогут построить тела (область V) в трехмерном пространстве.

z x		y	z	=1		z	z = 2x	z 2x + z = 1	z	z = 3
c	a	+b	+c	=1			2	z 2x + z = 1
c								1	3
								1	3
		b	y				y	y		y
a			y				y	1 2		y
a						1		1 2	x
					x	1		x	x

z = 1 - x - y

x + z = y

a +b

x2+ z2= 4

x = 1 - y2

z = 2 - y

y = x

Рис. 3.15

Пример 1. Вычислить интеграл ∫∫∫xyzdxdydz , где область V ограничена
					V
плоскостями:		x + z = 3, y = 2, y = 0, x = 0, z = 0.
Решение. Область V (рис. 3.16) правильная в направлении всех
переменных. Выберем следующий порядок интегрирования тройного
интеграла: внутренний интеграл – по z, средний – по y, внешний – по x.
	z			Стрелка, указывающая возрастание z, входит в
	3	x + z = 3		область V через границу z = 0 (нижний предел
y = 0	V	y = 2		интегрирования), а выходит из области V через
	D	2	y	границу z = 3 – x (верхний предел интегрирования).
3	D	z = 0		Стрелка,	указывающая	возрастание	y,	входит	в
3				область D (проекция области V на плоскость xOy)
x				область D (проекция области V на плоскость xOy)
	Рис. 3.16			через границу y = 0 (нижний предел), а выходит из
				через границу y = 0 (нижний предел), а выходит из
области D через границу y = 2 (верхний предел). Область D проектируется на
ось Ox в отрезок, границы которого 0 (нижний предел) и 3 (верхний предел).

			3	2	3−x			3		2			z	2	3−x

∫∫∫xyzdxdydz = ∫dx∫dy						∫xyzdz = ∫xdx∫ydy									=

V			0	0		0		0		0		2			0
= ∫3	xdx∫2	y	(3 − x)2	dy =	1	∫3	x(3	− x)2	y 2		2	=


0	0		2		2	0		2			0

		=	1		∫3 (9x − 6x2 + x3 )4dx
			4		0
					z
					9
					5	4z = y2
					1	V	6		9
					1	1	6		9
					1
					D		2x
		5					-
		5						y
						A(3;6)		=	0
						A(3;6)			0
					9
9				=
9			y
		+
	x	x
	x
						Рис. 3.17

	9		2		6		3		x	4	3		81			81		27
		x				x						=		−54	+		=		.
=				−				+
	2				3				4				2			4		4
											0

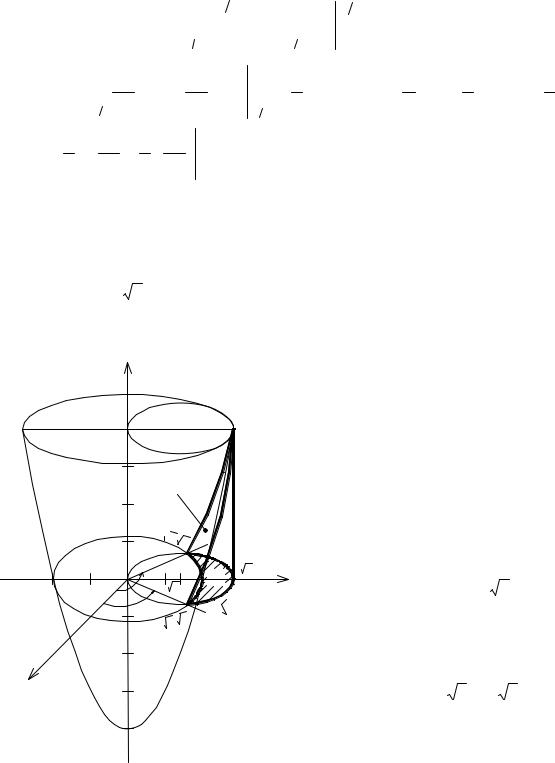
Пример 2. Найти объем тела, ограниченного поверхностями:

z = 0, 4z = y 2 , 2x − y = 0, x + y = 9 .

Решение. Область V (рис. 3.17) –

yправильная в направлении всех переменных – есть пирамида с вогнутой «крышей» – параболическим цилиндром 4z = y 2 , боковыми

гранями – плоскостями 2x − y = 0, x + y = 9 и

основанием (область D)

z = 0 ,

представляющим

собой

треугольник

вершиной A(3;6) , координаты

которой

находятся

решением

системы

уравнений: 2x − y = 0

x + y = 9.

V = ∫∫∫dxdydz = ∫6

9−y

dy ∫dx ∫dz = ∫6

dy ∫dx z y

y 2

9− y

y 2

9− y

dy x

9 − y −

9 y

−

= ∫dy ∫

dx = ∫

∫ y

dy =

∫

dy =

y 2

−

y 4

3888

= 40,5

ед. об.

648 −

Пример 3. Найти объем тела, ограниченного поверхностями

x2 + y 2 = 2 2 y , z = x2 + y 2 − 4 , z = 0 , z ≥ 0 .

Решение.

Область

(рис.

3.18)

–

правильная

направлении

переменной

Внутренний

интеграл

(по z) имеет нижний предел

интегрирования z = 0, верхний предел -

z = x2 + y 2

− 4 .

z = r2- 4

Область

(проекция

на

плоскость

xOy)

–

«полумесяц»,

B(-

2 ; 2 )

ограниченный

окружностями

D 2 2

-2

-1

3 π

1 2

x2 + y 2 − 4 = 0 , x2 + y2 = 2 2 y.

-1

)

Представим

эти

уравнения

(

-2

каноническом

виде:

-3

x2 + y2

= 22 , x2 + (y −

2 )2

= ( 2 )2 .

Видно,

-4

что внутренняя граница области D –

Рис. 3.18

окружность

радиусом

центром в начале координат, а внешняя граница – окружность с радиусом

r = 2 и смещенным вправо на 2 центром.

Вычисление тройного интеграла рациональнее произвести в

цилиндрической системе	координат	(r, φ, z). Воспользуемся связью:
x = r cosϕ , y = r sin ϕ , z=z и	преобразуем	уравнения поверхностей и кривых

данного примера в прямоугольных координатах в уравнения в цилиндрических координатах.

x2 + y2 = 2

2 y, r2 cos2 ϕ + r2 sin2 ϕ = 2

2r sinϕ ,

r 2

= 2

2r sin ϕ ; r = 2

2 sin ϕ . z = x2 + y2 −4, z = r 2 cos2 ϕ + r 2 sin 2 ϕ −4 ,

z = r 2 − 4 . При z = 0 получаем окружность r = 2. Найдем полярные углы

полярных

радиусов,

на

которых

находятся

точки

пересечения этих

r = 2

2 sin ϕ

окружностей:

= 2 2 sin ϕ ;

= sin

ϕ ;

ϕ1

; ϕ2

π .

r = 2

Анализ показывает, что тело V симметрично относительно плоскости x

= 0 (разделено пополам).

π 2

2 sinϕ

r 2 −4

π 2 2

2 sin ϕ

π 2

2 sin ϕ

V = ∫∫∫rdrdϕdz = 2 ∫dϕ

∫rdr

∫dz =

2 ∫dϕ

∫ rdr z

−4

= 2 ∫ dϕ

∫(r 3 − 4r)dr =

π 4

π 2

2 sinϕ

π 2

2 ∫dϕ

−

= 2 ∫

(16sin 4 ϕ −16sin 2 ϕ + 4)dϕ =

π 4

π 2

1 − cos 2ϕ

2 ∫

−16

+ 4 dϕ =

π 4

π2

=2 ∫(4 −8cos 2ϕ + 4cos2 2ϕ −8 +8cos 2ϕ + 4)dϕ =

π4

π 2	1+cos 4ϕ	dϕ = 4(ϕ +	1	sin 4ϕ )	π 2

= 8 ∫	2		4
π 4					π 4

= = 4 π	−	π		=π ед. об.
2		4

Пример 4. Найти объем тела, ограниченного поверхностями:

x2 + y 2 = 4 y, z = 6 − x2 , z = 0.

Решение. Данное тело (рис. 3.19) представляет собой круговой цилиндр с радиусом равным 2 и смещенным по «y» вправо на 2, сверху ограниченным параболическим цилиндром.

В основании цилиндра круг, поэтому вычисление объема проще всего проводить в цилиндрической системе координат. Подготовим все необходимые аналитические выражения для поверхностей и кривых, необходимых для вычисления объема тела.

				x = r cos ϕ, y = r sin ϕ.
z				Круговой цилиндр:
			x 2	+ y 2 = 4 y, r 2 cos2 ϕ + r 2 sin 2 ϕ = 4r sin ϕ, r 2	=
			= 4r sin ϕ, r = 4 sin ϕ.
				Это же уравнение и для окружности
			ограничивающей круг в основании тела, при		этом
2	4	y	0 ≤ϕ ≤ π.
x				Параболический цилиндр:
Рис. 3.19				z = 6 − x 2 , z = 6 − r 2 cos2 ϕ.
				z = 6 − x 2 , z = 6 − r 2 cos2 ϕ.

Вычислим объем тела.

					π		4sinϕ		6 −r 2 cos 2 ϕ			π		4sinϕ						6−r 2 cos 2 ϕ π		4sinϕ
V = ∫∫∫rdrdϕdz = ∫dϕ ∫rdr										∫dz = ∫dϕ ∫rdr z											=∫dϕ		∫(6 − r2 cos2 ϕ)rdr =
	V			0			0			0		0				0			0		0			0
π	4sin	ϕ	3			2			π		2		1		4	2				4sinϕ	π		2		4	2
π	4sin	ϕ	3			2			π		2		1		4	2				4sinϕ	π		2		4	2
= ∫dϕ ∫		(6r − r		cos			ϕ)dr	=	∫dϕ 3r			−		r		cos	ϕ				=∫(48sin			ϕ − 64sin		ϕ cos	ϕ)dϕ =
= ∫dϕ ∫		(6r − r		cos			ϕ)dr	=	∫dϕ 3r			−	4	r		cos	ϕ				=∫(48sin			ϕ − 64sin		ϕ cos	ϕ)dϕ =
0	0								0				4							0	0
π	1− cos 2ϕ						1	−cos 2ϕ 2				1	+ cos 2ϕ
= ∫ 48						−64												dϕ =
= ∫ 48		2				−64				2					2			dϕ =
0		2								2					2

=π∫[24 − 24cos 2ϕ −8(1− 2cos 2ϕ + cos2 2ϕ)(1+ cos 2ϕ)]dϕ =

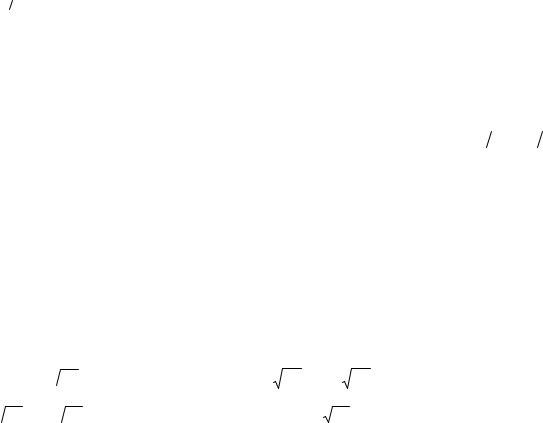
= π∫(24 − 24cos 2ϕ −8 +16cos 2ϕ −8cos2 2ϕ −8cos 2ϕ +16cos2 2ϕ −8cos3 2ϕ)dϕ =

=π∫(16 −16cos 2ϕ + 8cos2 2ϕ −8cos3 2ϕ)dϕ =

1 + cos 4ϕ

∫

−

16cos 2ϕ + 8

dϕ −

∫4 cos

2ϕd sin 2ϕ =

= π∫(20

−16cos 2ϕ + 4 cos 4ϕ)dϕ −π∫4(1 − sin2

2ϕ)d sin 2ϕ =

= (20ϕ −8sin 2ϕ + sin 4ϕ)

− 4 sin 2ϕ −

sin

2ϕ

= 20π ед.объема.

3.3.5. Задания на контрольную работу

Задание 1. Вычислить.

			x = 0, y =1, y = x,
1.∫∫∫y2e2 xy dxdydz;V :					z = 0, z = 8.
V					z = 0, z = 8.
			x	= 0, y = 2, y = 2x,
3.∫∫∫y 2 exy 2 dxdydz;V :				z	= 0, z = −1.
V				z	= 0, z = −1.
5.∫∫∫y	2		πxy		x = 0, y = −1, y				=
5.∫∫∫y		cos	dxdydz;V :			z = 0, z = 2π			2	.
V			2			z = 0, z = 2π				.
7.∫∫∫y 2				x = 0, y =1, y = 2x,
7.∫∫∫y 2		cos(πxy)dxdydz;V :				z = 0, z = π	2	.
V						z = 0, z = π		.
			x = −1, y = x, y = 0,
9.∫∫∫x2 e2 xy dxdydz;V :				z	= 0, z = 8.
V				z	= 0, z = 8.

							x = 2, y		=1, z =1,
2.∫∫∫x2 ze xyz dxdydz;V :								= 0, y = 0, z = 0.
V							x	= 0, y = 0, z = 0.
4.∫∫∫y 2 z cos			xyz					x = 3, y =1, z = 2π,
			xyz			dxdydz;V :
						dxdydz;V :
V				3				x = 0, y = 0, z = 0.
							x =1, y		= −1, z =1,
6.∫∫∫2x2 ze xyz dxdydz;V :
V							x = 0, y = 0, z = 0.
							x = 2, y		=1 2, z =1 2,
8.∫∫∫3xze2 xyz dxdydz;V :								x = 0, y = 0, z = 0.
V								x = 0, y = 0, z = 0.
10.∫∫∫x	2		xyz					x	=1, y = 4, z = π,
		z sin					dxdydz;V :		= 0, y = 0, z = 0.
		z sin					dxdydz;V :
V					2			x

Задание2. Найти объем тела, заданного ограничивающими его поверхностями.

1.x + y = 4, y = 2x, z = 3y, z = 0.

3.y = 6 3x, y = 3x, z = 0, x + z = 3.

2.	x =19 2y, x = 4 2y, z = 0, z + y = 2.
4.	x + y = 6, y = 3x, z = 4 y, z = 0.

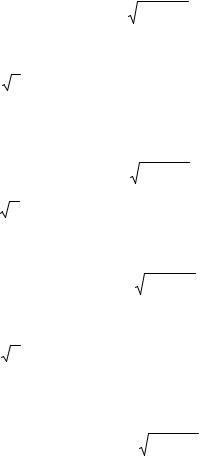
5.	y = 2x2 , z + y = 2, z = 0.	6.	x2 = y −1, x + y + z = 3, z = 0.
7.	y 2 = 4 − x, x = z, z = 0.	8.	y2 = x + 4, x + z = 0, z = 0.
9.	y2 = x, x + z = 4, x =1, z = 0.	10. y = x2 , y + z = 9, y =1, z = 0.

Задание 3. Найти объем тела, заданного ограничивающими его поверхностями.

1. x2 + y 2 = 6x, x2 + y 2 = 9x, z = x2 + y 2 , z = 0,

y = 0 (y ≤ 0).

2.	x2	+ y 2	= 6 2 y, z = x2 + y 2 − 36, z = 0 (z ≥ 0).
3.	x2 + y 2 = 2 y, z =			9	− x2 , z = 0.
				4

4.	x2 + y 2 = 2 y, x2 + y 2 = 5y, z = x2 + y 2 , z = 0.
5.	x2 + y 2 + 2 2 y = 0, z = x2 + y 2 − 4, z = 0 (z ≥ 0).
6.	x2 + y 2 = 4x, z =10 − y 2 , z = 0.
7.	x2	+ y 2	= 7x, x2 + y 2 =10x, z = x2 + y 2 , z = 0,
y = 0 (y ≤ 0).
8.	x2	+ y 2	= 8 2 y, z = x2 + y 2 − 64, z = 0 (z ≥ 0).
9.	x2	+ y 2	= 2 y, z =	13		− x2 , z = 0.
				4

10. x2 + y 2 = 3y, x2				+ y 2 = 6 y, z = x2 + y 2 , z = 0.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2713 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.11.20183.81 Mб187Подвижной состав. Исправленное.doc
#
30.12.201984.44 Mб1Пособие 80Р.doc
#
12.11.2019176.64 Кб14пособие для поведния семинрских знятий.doc
#
15.02.201530.97 Mб33пособие проводнику.docx
#
15.02.201523.98 Кб26почтовобагажный вагон.docx
#
15.02.20153.83 Mб107практикум математика часть 2.pdf
#
15.02.20154.76 Mб123практикум по математике часть 3.pdf
#
15.02.2015328.84 Кб49Практич_МТТ_с_приложением_МТТ.pdf
#
15.02.2015439.81 Кб35Практическое занятие.doc
#
18.09.201934.46 Кб6Предпринимательство.docx
#
15.02.201530.21 Кб14прием док-в в общ-е (1).doc