
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf
294 |
Г л а в а 5. Химическая кинетика |
кДж моль–1, то понятно, что слабая температурная зависимость предэкспоненциального множителя вносит лишь очень небольшой вклад в экспериментально измеряемую энергию активации.
Аномальную зависимость константы скорости от температуры проявляют некоторые реакции третьего порядка, а также цепные и ферментативные реакции. В реакциях третьего порядка константа скорости убывает с ростом температуры:
k
T
Течение ферментативных реакций может осложняться денатурацией фермента, поэтому эффективная константа скорости при нагревании сначала возрастает, а затем убывает:
k
T
В цепных экзотермических реакциях возможно явление «теплового взрыва», при котором константа скорости резко возрастает при температуре выше некоторого предела:
k
T
ПРИМЕРЫ
Пример 20-1. Пользуясь уравнением Аррениуса, оцените, при каких температурах и энергиях активации справедливо правило ВантГоффа.
Решение. Представим правило Вант-Гоффа (20.1) как степенную зависимость константы скорости:

Г л а в а 5. Химическая кинетика |
295 |
|||
k(T ) = B γ (T / 10) , |
|
|
|
|
где B – постоянная величина. Сравним это выражение с уравнением |
|
|||
Аррениуса (20.2), приняв для температурного коэффициента скорости |
|
|||
значение γ ~ e = 2.718: |
|
|
|
|
|
E |
A |
|
|
B γ (T / 10) ≈ A exp − |
|
. |
|
|
|
|
|
||
|
RT |
|
||
Возьмем натуральный логарифм обеих частей этого приближенного равенства:
ln B + 10T ln γ ≈ ln A − RTEA .
Продифференцировав полученное соотношение по температуре, найдем искомую связь между энергией активации и температурой:
EA |
≈ |
RT |
2 |
ln γ . |
10 |
|
|||
|
|
|
|
Если учесть, что γ принимает значения в интервале 2 < γ < 4, то соответствующий диапазон изменения энергий активации равен:
T22 < EA < T 2 .
Если энергия активации (в Дж моль–1) попадает в этот интервал, то при данной температуре правилом Вант-Гоффа для оценки влияния температуры на скорость реакции пользоваться можно.
Пример 20-2. Реакция первого порядка при температуре 70 °С завершается на 40% за 60 мин. При какой температуре реакция завершится на 80% за 120 мин, если энергия активации равна 60 кДж моль–1?
Решение. Для реакции первого порядка константа скорости выражается через степень превращения следующим образом:
k = |
1 |
ln |
a |
= − |
1 |
ln (1 − α) , |
|
a − x |
|
||||
|
t |
|
t |
|||
где α = x/a – степень превращения.
Запишем это уравнение при двух температурах с учетом уравнения Аррениуса:
A exp − |
|
EA |
|
= − |
|
1 |
|
ln (1 − α1 ), |
|
RT1 |
|
|
|||||
|
|
|
|
|
t1 |
|||
A exp − |
|
EA |
= − |
|
1 |
ln (1 − α 2 ), |
||
RT2 |
|
|
||||||
|
|
t2 |
||||||
где EA = 60 кДж моль–1, T1 = 343 K, t1 = 60 мин,α1 = 0.4, t2 = 120 мин, α2 = 0.8.

296 |
Г л а в а 5. Химическая кинетика |
Поделим одно уравнение на другое и прологарифмируем:
EA |
|
1 |
1 |
|
t2 ln(1 − α1 ) |
|
|||||||
|
|
|
|
− |
|
|
= ln |
|
|
|
|
|
. |
R |
T |
2 |
T |
t |
1 |
ln(1 − α |
2 |
) |
|||||
|
|
|
1 |
|
|
|
|
|
|||||
Подставляя в это выражение приведенные выше значения, находим
T2 = 351 К = 78 °С.
Пример 20-3. Скорость бактериального гидролиза мышц рыб удваивается при переходе от температуры –1.1 °С к температуре +2.2 °С. Оцените энергию активации этой реакции.
Решение. Увеличение скорости гидролиза в 2 раза обусловлено увеличением константы скорости: k2 = 2k1. Энергию активации по отношению констант скорости при двух температурах можно опреде-
лить из уравнения (20.3) с T1 = t1 + 273.15 = 272.05 K, T2 = t2 + 273.15 = = 275.35 K:
EA = 8.314 272.05 275.35 ln 2 = 1.3 105 Дж моль–1 = 130 кДж моль–1. 3.3
Пример 20-4. Для реакции термического разложения N2O5 энергия активации равна 103.5 кДж моль–1, а предэкспоненциальный множитель в уравнении Аррениуса равен 4.6 1013 с–1. Рассчитайте:
а) период полураспада реагента при –10 °С; б) время, необходимое для завершения реакции на 90% при 50 °С. Решение. Рассчитаем константы скорости:
k–10 = 4.6 1013 exp[–103500 / (8.314 263)] = 1.28 10–7 с–1, k50 = 4.6 1013 exp[–103500 / (8.314 323)] = 8.40 10–4 с–1,
Период полураспада при температуре –10 °С:
τ1/2 = ln 2 / (1.28 10–7) = 5.42 106 с = 62.7 сут.
Время 90%-ного завершения реакции при температуре 50 °С:
τ = ln 10 / (8.40 10–4) = 2740 с = 45.7 мин.
ЗАДАЧИ
20-1. С помощью правила Вант-Гоффа вычислите, при какой температуре реакция закончится через 15 мин, если при 20 °С на это требуется 2 ч. Температурный коэффициент скорости равен 3.
20-2. Время полураспада вещества при 323 К равно 100 мин, а при 353 К – 15 мин. Определите температурный коэффициент скорости.

Г л а в а 5. Химическая кинетика |
297 |
20-3. Какой должна быть энергия активации, чтобы скорость реакции увеличивалась в 3 раза при возрастании температуры на 10 °С:
а) при 300 К;
б) при 1000 К?
20-4. Реакция первого порядка имеет энергию активации 25 ккал моль–1 и предэкспоненциальный множитель 5 1013 с–1. При какой температуре время полураспада для данной реакции составит:
а) 1 мин; б) 30 дней?
20-5. Энергия активации реакции, приводящей к скисанию молока, равна 75 кДж моль–1. При температуре 21 °С молоко скисает за 8 ч. Как долго можно хранить молоко в холодильнике при температуре 5 °С? Время скисания можно принять обратно пропорциональным константе скорости.
20-6. В каком из двух случаев константа скорости реакции увеличивается в большее число раз: при нагревании от 0 °С до 10 °С или при нагревании от 10 °С до 20 °С? Ответ обоснуйте с помощью уравнения Аррениуса.
20-7. Используя дифференциальную форму уравнения Аррениуса, выведите связь между энергиями активации прямой и обратной реакций, в предположении, что прямая и обратная реакции – элементарные.
20-8. Энергия активации некоторой реакции в 1.5 раза больше, чем энергия активации другой реакции. При нагревании от T1 до T2 константа скорости второй реакции увеличилась в a раз. Во сколько раз увеличилась константа скорости первой реакции при нагревании от T1 до T2?
20-9. Константа скорости сложной реакции выражается через константы скорости элементарных стадий следующим образом:
k = k1k2 . k3
Выразите энергию активации и предэкспоненциальный множитель сложной реакции через соответствующие величины, относящиеся к элементарным стадиям.
20-10. В необратимой реакции первого порядка за 20 мин при 125 °С степень превращения исходного вещества составила 60%, а при 145 °C такая же степень превращения была достигнута за 5.5 мин. Найдите константы скорости и энергию активации данной реакции.
298 |
Г л а в а 5. Химическая кинетика |
20-11. Реакция первого порядка при температуре 25 °С завершается на 30% за 30 мин. При какой температуре реакция завершится на 60% за 40 мин, если энергия активации равна 30 кДж моль–1?
20-12. Реакция первого порядка при температуре 25 °С завершается на 70% за 15 мин. При какой температуре реакция завершится на 50% за 15 мин, если энергия активации равна 50 кДж моль–1?
20-13. Константа скорости реакции первого порядка равна 4.02 10–4 с–1 при 393 К и 1.98 10–3 с–1 при 413 К. Рассчитайте предэкспоненциальный множитель для этой реакции.
20-14. Для газофазной реакции HI + CH3I → CH4 + I2 энергия активации равна 140 кДж моль–1. Константа скорости при 227 °С равна 3.9 10–3 л моль–1 с–1. Рассчитайте константу скорости при 310 °С. При какой температуре константа скорости будет равна 1.0 10–3 л моль–1 с–1?
20-15. Для реакции
H2 + I2 → 2HI
константа скорости при температуре 683 К равна 0.0659 л моль–1 мин–1, а при температуре 716 К – 0.375 л моль–1 мин–1. Найдите энергию активации этой реакции и константу скорости при температуре 700 К.
20-16. Для реакции
2N2O → 2N2 + O2
константа скорости при температуре 986 К равна 6.72 л моль–1 мин–1, а при температуре 1165 К – 977.0 л моль–1 мин–1. Найдите энергию активации этой реакции и константу скорости при температуре 1053.0 К.
20-17. Трихлорацетат-ион в ионизирующих растворителях, содержащих H+, разлагается по уравнению
H+ + CCl3COO– → CO2 + CHCl3.
Стадией, определяющей скорость реакции, является мономолекулярный разрыв связи C−C в трихлорацетат-ионе. Реакция протекает по
первому порядку, и константы скорости имеют следующие значения: k = 3.11 10–4 с–1 при 90 °С, k = 7.62 10–5 с–1 при 80 °С. Рассчитайте:
а) энергию активации, б) константу скорости при 60 °С.
20-18. Используя справочные данные, рассчитайте период полураспада бромэтана на этилен и бромоводород при:
а) 100 °С; б) 400 °С.

Г л а в а 5. Химическая кинетика |
299 |
20-19. Используя справочные данные, рассчитайте период полураспада иодоводорода на иод и водород при начальной концентрации 0.05 моль л–1 и температуре:
а) 600 °С; б) 900 °С.
20-20. Раскручивание двойной спирали ДНК – реакция первого порядка с энергией активации 420 кДж моль–1. При 37 °С константа скорости равна 4.90 10–4 мин–1. Рассчитайте период полупревращения ДНК при
37 и 40 °С.
20-21. Для реакции
CH3COOC2H5 + NaOH → CH3COONa + C2H5OH
константа скорости при температуре 282.6 К равна 2.307 л моль–1 мин–1, а при температуре 318.1 К – 21.65 л моль–1 мин–1. Найдите энергию активации этой реакции и константу скорости при температуре 343 К.
20-22. Для реакции
C12H22O11 + H2O → C6H12O6 + C6H12O6
константа скорости при температуре 298.2 К равна 0.765 л моль–1 мин–1, а при температуре 328.2 К – 35.5 л моль–1 мин–1. Найдите энергию активации этой реакции и константу скорости при температуре 313.2 К.
20-23. Вещество разлагается двумя параллельными путями с константами скорости k1 и k2. Какова разность энергий активации этих двух ре-
акций, если при 10 °C k1/k2 = 10, а при 40 °C k1/k2 = 0.1?
20-24. В двух реакциях одинакового порядка разница энергий активации составляет E2 – E1 = 40 кДж моль–1. При температуре 293 К отношение констант скорости равно k1/k2 = 2. При какой температуре константы скорости сравняются?
20-25. Зависимость константы скорости разложения фосфина 4PH3 → P4 + 6H2 от температуры выражается уравнением:
lg k = − 1896T + 2 lg T + 12.130.
Рассчитайте опытную энергию активации этой реакции при 800 К.
20-26. Разложение ацетондикарбоновой кислоты в водном растворе – реакция первого порядка. Измерены константы скорости этой реакции при разных температурах:
t, °С |
0 |
20 |
40 |
60 |
k 105, с–1 |
2.46 |
47.5 |
576 |
5480 |


302 |
Г л а в а 5. Химическая кинетика |
Уравнения (21.3) для обратимой реакции первого порядка имеют такой же вид, как и для необратимой реакции (18.3), (18.4) с той разницей, что вместо начальной концентрации фигурирует равновесная, а константу скорости необратимой реакции заменяет сумма констант для прямой и обратной реакций.
При t → ∞ наступает равновесие, которое характеризуется константой:
|
(21.5) |
K = |
[B]∞ |
= b + x∞ |
= k1 . |
|
|
|
[A]∞ |
a − x∞ |
k−1 |
|
|
Кинетические кривые для обратимых реакций первого порядка при- |
|||
|
|
ведены на рис. 21.1. |
|
|
|
|
|
(1) |
|
|
(1) |
a |
AA VBB |
a |
|
|
|
|
|
|
|
|
x∞ |
c |
|
B |
c |
|
A |
|
|
A |
B |
||
|
|
A |
|
|
Aς B |
|
|
|
|
B |
|
|
|
x∞ |
|
|
x∞ |
|
|
t |
|
|
t |
|
Рис. 21.1 |
Зависимость концентраций реагента и продукта от времени |
|||
|
|
для обратимой реакции первого порядка: (1) K > 1; (2) K < 1 |
|||
2. Параллельные реакции:
k1 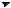 B
B
A k2
D .
Кинетическое уравнение записывается с учетом принципа независимости:
(21.6) |
dx |
= k1 (a − x) + k2 (a − x) . |
|
dt |
|||
|
|
Решение этого уравнения записывается так же, как и для одной реакции первого порядка:
(21.7.а) |
(k1 + k2 )t = ln |
a |
|
, |
|
a − x |
|||||
|
|
|
|||
(21.7.б) |
[A] = a − x = a exp[−(k1 |
+ k2 )t]. |
|||

|
|
|
|
|
Г л а в а 5. Химическая кинетика |
303 |
|||
|
Для |
|
параллельных |
реак- |
a |
AA→T B |
|
||
|
|
|
|
||||||
ций в любой момент времени |
|
A T D |
|
||||||
отношение концентраций про- |
|
A → D |
|
||||||
c |
B |
|
|||||||
дуктов постоянно и определя- |
|
|
|||||||
|
|
|
|||||||
ется |
константами |
скорости |
|
D |
|
||||
элементарных стадий: |
|
|
|
||||||
|
|
|
|
||||||
[B] |
= |
k1 |
. |
|
(21.8) |
|
A |
|
|
[D] |
k |
|
|
|
t |
|
|||
|
2 |
|
|
|
|
|
|||
|
Кинетические кривые для |
Зависимость концентраций реагентов и |
|
||||||
|
продукта от времени для параллельных |
|
|||||||
случая двух параллельных ре- |
|
||||||||
|
реакций первого порядка, k1 > k2 |
Рис. 21.2 |
|||||||
акций первого порядка приве- |
|
|
|
||||||
дены на рис. 21.2. |
|
|
|
|
|
||||
3. Последовательные реакции:
A |
k1 |
B |
k2 |
D . |
|
|
К таким реакциям относится, например, гидролиз сложных эфиров дикарбоновых кислот.
Пусть в начальный момент времени есть только вещество A. Применим к этой системе закон действующих масс и принцип независимости химических реакций:
d[A] |
= −k1[A] |
|
a |
D |
|
|
dt |
|
|
||
|
|
|
A |
||
d[B] |
= k1[A] − k2 [B] |
(21.9) |
|
|
|
|
dt |
|
|
||
|
|
|
c |
A → B → D |
|
d[D] |
= k2 [B] |
|
|
A T B T D |
|
|
|
|
|||
|
dt |
|
|
|
|
с начальными условиями |
|
B |
|||
[A]0 = a, [B]0 = [D]0 = 0. |
|
|
t |
||
|
|
|
|
|
|
Решение |
этой |
системы |
Зависимость концентраций веществ |
Рис. 21.3 |
||||
дает |
концентрации |
веществ |
от времени в системе двух |
|||||
|
||||||||
|
||||||||
как |
функции |
времени (рис. |
последовательных реакций |
|
||||
21.3): |
|
|
|
|
первого порядка при k1 / k2 = 0.2 |
|
||
|
|
|
|
|
|
|||
|
|
[A] = a exp(−k1t) |
|
|||||
|
|
|
|
|
k1 |
|
|
|
|
|
|
|
|
[exp(−k1t) − exp(−k2 t)] |
(21.10) |
||
|
|
[B] = a |
|
|
||||
|
|
k2 |
− k1 |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
[D] = a − [A] − [B] . |
|
|||||

 B .
B .