7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с

Добавил:

Sahsha Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Физическая химия

Файл:

2 d ln k(T )

.pdf

Скачиваний:

Добавлен:

02.01.2023

Размер:

5.51 Mб

Скачать

☆

<<< < Предыдущая 24 25 26 27 28 29 30 31 32 33 34 35 3637 / 4837 38 39 40 41 42 43 44 45 46 47 48 > Следующая >>>

364	Г л а в а 5. Химическая кинетика

(25.15)

(25.16)

(25.17.а)

(25.17.б)

(25.18)

и описывает кинетику реакции первого порядка. При низких давлениях: k2[M] << k3, когда дезактивацией молекул можно пренебречь и все активированные молекулы вступают в реакцию,

r = k1[M][A] .

Реакция имеет общий второй порядок, а ее скорость определяется скоростью активации молекул при столкновениях.

В общем случае эффективная константа скорости первого порядка

kI	=	k1k3 [M]
		k2	[M] + k3

зависит от общей концентрации частиц в системе и возрастает при увеличении концентрации от kI = k1[M] при низких концентрациях до k∞ при высоких.

Таким образом, схема Линдемана предсказывает возрастание эффективной константы скорости первого порядка и изменение порядка мономолекулярной реакции со второго на первый при увеличении концентрации частиц. Считается, что переход от второго порядка к первому происходит, когда константа скорости (25.16) составляет половину от максимально возможной (в уравнении (25.14)):

	1		1 k1k3		.

kI = 2 k∞ =			2 k2
kI = 2 k∞ =			2 k2
Это имеет место при концентрации
[M]1 / 2 =		k3	=	k∞	.
[M]1 / 2 =		k2	=		.
		k2		k1

Соответствующее этой концентрации давление называют давлением пе-

рехода.

Эти выводы качественно правильно описывают кинетику мономолекулярных реакций в газовой фазе. В то же время оказалось, что для большинства реакций константы скорости активации k1, рассчитанные по формуле (25.12), на несколько порядков ниже экспериментальных значений, а давления перехода – намного больше экспериментальных

(см. задачу 25-7).

Для того, чтобы добиться лучшего согласия теории с экспериментом, Хиншельвуд предположил, что активация молекул в рамках схемы Линдемана происходит за счет не только поступательной энергии сталкивающихся частиц, но и за счет внутренних степеней свободы – главным образом, колебательных. Если в активации, помимо поступательных, участвуют f колебательных степеней свободы, то константа скорости активации имеет вид:

	EA f
					EA
		RT			EA
k1	= z0 N A		exp	−		.
k1	= z0 N A	f !	exp	−	RT	.
		f !			RT

Г л а в а 5. Химическая кинетика

365

В рамках этой теории число внутренних степеней свободы f является эмпирическим параметром и определяется по экспериментальным данным.

Схема Линдемана послужила основой для многих более сложных теорий мономолекулярных реакций. Все теории этого типа основаны на учете зависимости констант скорости активации и распада от энергии, при этом рассматривается активация в малый интервал энергий от E до

E + δE:

A + M → A(E→ E + δE ) + M ,		(25.19.а)
δk1	*
A(E→ E + δE) + M → A + M ,		(25.19.б)
*	k2
A(E )	→ P ,	(25.19.в)
*	ka (E)

Применение квазистационарного приближения к этой схеме дает выражение, аналогичное (25.16), для вклада активных молекул с энергией от E до E + δE в константу скорости:

	ka (E)	δk1(E→ E + δE)
δkI(E→ E + δE ) =	ka (E)		k2	.	(25.20)
			k2
	1 +		ka (E)
			ka (E)
			k2 [M]

Полная константа скорости мономолекулярной реакции получается интегрированием (25.20) по всем возможным энергиям активации:

	ka (E)	dk1(E→ E + δE)
∞		k2
kI = ∫			.	(25.21)
		ka (E)

EA 1 + k2 [M]

В теории РРКМ (Райса–Рамспергера–Касселя–Маркуса), вводится различие между активной молекулой A* и активированным комплексом A+, и реакция (25.19.в) записывается в две стадии:

A	*	ka (E )	+	k +	(25.22)
A	(E )	→ A		→ P .	(25.22)

Активная молекула обладает достаточной энергией, чтобы вступить в реакцию, однако распределение энергии в молекуле не позволяет ей сразу превратиться в реагенты, для этого сначала должна быть достигнута конфигурация активированного комплекса. В теории РРКМ константу скорости k1 рассчитывают с помощью квантовых методов, а константу ka – по теории активированного комплекса.

366

Г л а в а 5. Химическая кинетика

Теория активированного комплекса

Современные теории химической кинетики основаны на анализе

движения ядер по поверхности потенциальной энергии системы реаги-

рующих частиц. Для описания химической реакции решают классиче-

ские или квантовые уравнения движения, а константы скорости находят

из полученных решений – классических траекторий, волновых функ-

ций, функций распределения и т.д.

Для системы, содержащей N атомов, потенциальная энергия зависит

от n = 3N – 6 (для нелинейной

системы) или n = 3N – 5 (ли-

нейная молекула) координат и

может

быть

представлена ги-

перповерхностью

размерности

X-Y

n + 1. Для наглядного представ-

ления

этой

гиперповерхности

используют

сечения

вдоль

координат,

существенных для

протекающей реакции. Напри-

мер, при диссоциации линей-

ной

трехатомной

молекулы

Расстояние Y1-X

YXY → YX + Y потенциаль-

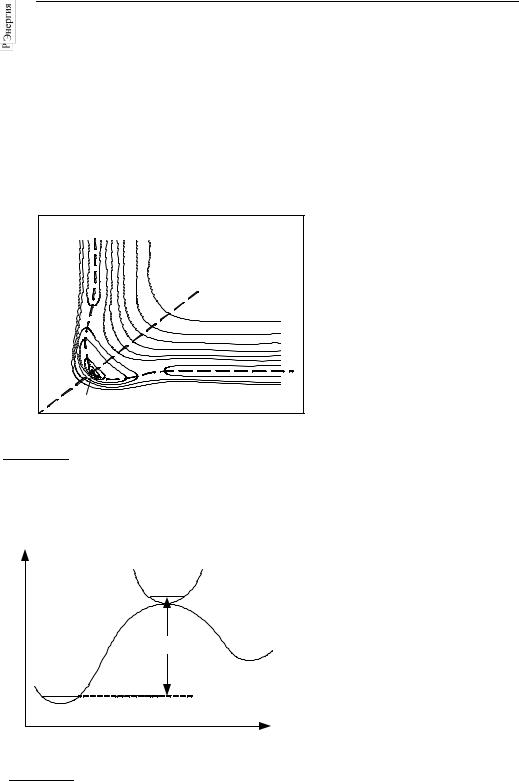
Рис. 25.1

Поверхность потенциальной энергии

ную

энергию можно

предста-

вить как функцию двух межъя-

для симметричной трехатомной

дерных

расстояний,

для

молекулы YXY. Симметричное

колебание происходит вдоль линии AB,

изображения

которой

исполь-

а асимметричное, приводящее к

зуют линии уровня (рис. 25.1).

распаду, – вдоль линий OC или OD.

Одномерную кривую, ха-

рактеризующую путь с наи-

(Y1···XY2)‡

меньшей энергией, по которому

происходит реакция,

называют

координатой реакции.

Сечение

поверхности вдоль этой кривой

дает

профиль

потенциальной

энергии для реакции (рис. 25.2),

на котором имеется максимум.

Все конфигурации ядер, соот-

ветствующие

малой

области

вблизи этого максимума, назы-

Координата реакции

вают

активированным

ком-

плексом,

или

переходным

Рис. 25.2

Профиль потенциальной энергии

состоянием

для

данной

реак-

для реакции YXY → Y + XY.

ции. Активированный комплекс

Координата реакции – расстояние

можно

рассматривать

как

вдоль линии OC на рис. 25.1

обычную молекулу с той раз-

Г л а в а 5. Химическая кинетика

367

ницей, что одна колебательная степень свободы заменена на поступательное движение вдоль координаты реакции. Разница между нулевыми энергиями колебаний активированного комплекса и реагентов составляет энергию активации реакции E0.

В теории активированного комплекса (ТАК) элементарную реакцию рассматривают как одномерное поступательное движение по координате реакции. Для расчета констант скорости используют следующие допущения.

1.Молекулярная система, движущаяся по поверхности потенциальной энергии в направлении продуктов реакции и достигшая вершины барьера, неизбежно превращается в продукты реакции.

2.Движение по пути реакции может быть описано в терминах классической механики без учета квантовых эффектов.

3.Элементарная реакция происходит адиабатически, т.е. без перехода на другую поверхность потенциальной энергии.

4.Элементарную реакцию представляют как мономолекулярный распад активированного комплекса по схеме:

реагенты

акт. комплекс

продукты

Предполагается, что химическая реакция протекает без нарушения равновесного распределения молекул реагентов по энергиям, а между реагентами и активированным комплексом существует квазиравновесие, поэтому концентрацию активированных комплексов можно выразить через термодинамическую константу равновесия.

Основное уравнение теории активированного комплекса – уравне-

ние Эйринга – имеет вид:

k(T ) = kBhT K c≠ ,

где kB – постоянная Больцмана, h – постоянная Планка, K c≠ – константа

равновесия образования активированного комплекса, выраженная через молярные концентрации (в моль л–1).

Взависимости от того, как рассчитывают константу равновесия, различают статистический и термодинамический аспекты ТАК.

Встатистическом подходе константу равновесия выражают через суммы по состояниям (см. формулу (16.17)):

≠

kBT

N V

k(T ) =

exp

−

Qi,реаг

∏

N AV

где Q ≠ – полная сумма по состояниям активированного комплекса, Qi,реаг – суммы по состояниям реагентов, E0≠ – энергия активации при

(25.23)

(25.24)

368		Г л а в а 5. Химическая кинетика
		абсолютном нуле, которая представляет собой разницу между нулевы-
		ми энергиями активированного комплекса и реагентов (рис. 25.2).
		Полные суммы по состояниям обычно разлагают на сомножители,
		соответствующие отдельным видам движения молекул: поступательно-
		му, электронному, вращательному и колебательному:
(25.25)		Q = Qпост Qэл Qвращ Qкол.

(25.26)

(25.27)

Поступательную сумму по состояниям для частицы массой m рассчитывают по формуле (15.34). Электронная сумма по состояниям при обычных температурах, как правило, постоянна и равна вырожденности основного электронного состояния: Qэл = g0.

Вращательную сумму по состояниям для двухатомной молекулы (15.40) можно выразить через приведенную массу молекулы µ и межъядерное расстояние r:

Qвращ = 8π 2 µr 2 kBT ,

σh2

где µ = m1m2 / (m1 + m2), число симметрии σ = 1 для несимметричных молекул XY и σ = 2 для симметричных молекул X2.

Для линейных многоатомных молекул вращательная сумма по состояниям пропорциональна T, а для нелинейных молекул – T3/2. При обычных температурах вращательные суммы по состояниям имеют по-

рядок 101–102.

Колебательная сумма по состояниям молекулы записывается как произведение сомножителей, каждый из которых соответствует опре-

деленному колебанию:
Qкол =	n		− exp	−	Tкол,i	−1
		1				,
		1				,
	∏				T
	i=1				T

где n – число колебаний (для линейной молекулы, состоящей из N ато-

мов, n = 3N – 5, для нелинейной молекулы n = 3N – 6), Tкол,i – эффективная колебательная температура (15.42) для i-го колебания.

При обычных температурах колебательные суммы по состояниям очень близки к 1 и заметно отличаются от нее только при условии: T > Tкол. При высоких температурах колебательная сумма для каждого колебания прямо пропорциональна температуре – см. (15.44).

Отличие активированного комплекса от обычных молекул состоит в том, что он имеет на одну колебательную степень свободы меньше, а именно: то колебание, которое приводит к распаду комплекса, не учитывается в колебательной сумме по состояниям.

Принципиальная проблема статистического варианта ТАК состоит в том, что во многих случаях точное строение активированного комплекса неизвестно и поэтому статистические суммы комплекса можно оценивать лишь с известной долей погрешности.

Г л а в а 5. Химическая кинетика

369

Рассмотрим применение ТАК к бимолекулярным реакциям. Простейшая бимолекулярная реакция – столкновение атомов:

X + Y [XY]≠ → XY.

Активированный комплекс в этой реакции – это двухатомная молекула, обладающая только вращательными и поступательными степенями свободы (единственное колебание в активированном комплексе исключено). Согласно уравнению Эйринга,

k T

пост

(XY≠ )

эл

(XY≠ )

≠

k(T ) =

N V

вращ

(XY≠ )

exp −

пост

(X)Q

пост

(Y)

эл

(X)Q

эл

(Y)

Подставляя сюда поступательные суммы по состояниям (15.34) и вращательную сумму (25.26), находим:

8πk T 1/ 2

эл

(XY ≠ )

≠

k(T ) = r 2

exp −

XY ≠

(X)Q

(Y)

эл

(25.28)

(25.29)

Сравнивая (25.29) с уравнением Траутца–Льюиса (25.8) и (25.3), видим, что ТАК и ТАС дают очень близкие выражения для константы скорости реакции столкновения двух атомов, если считать, что электронный фактор равен 1, а межъядерное расстояние в активированном комплексе равно сумме радиусов атомов: rXY = rX + rY. Эта аналогия позволяет дать статистическую интерпретацию стерическому фактору в ТАС.

Рассмотрим столкновение двух нелинейных молекул X и Y, состоящих из n и m атомов. Для этой бимолекулярной реакции константа скорости имеет вид:

k(T ) =

k T

N V

пост

(XY ≠ )

Qвращ(XY ≠ )

Qпост(X)Qпост(Y)

Qвращ(X)Qвращ(Y)

кол

(XY ≠ )

E ≠

exp

−

(X)Q

(Y)

кол

Введем понятие суммы по состояниям в расчете на одну степень свободы q и предположим, что эти суммы одного и того же типа для всех молекул одинаковы по порядку величины:

			Q	= q3	,
			пост	пост
	q3		для нелинейных молекул
Qвращ		вращ
Qвращ	=	2	для линейных молекул,
	qвращ		для линейных молекул,

	q3N −6		для нелинейных молекул
Qкол		кол
Qкол	=		для линейных молекул.
	q3N −5		для линейных молекул.
		кол

(25.30)

(25.31.а)

(25.31.б)

(25.31.в)

370	Г л а в а 5. Химическая кинетика

Перепишем (25.28) и (25.30) с учетом (25.31). Для столкновения атомов:

		k T		q3					E	≠
(25.32.а)	k(T ) =	B	N V	пост		q 2	exp	−		0	.
	k(T ) =	h	N V			q 2	exp	−			.
		h	A	q3	q3	вращ			RT
				пост	пост

Константа скорости бимолекулярной реакции между нелинейными молекулами:

(25.32.б)

(25.33)

(25.34)

(25.35)

k T

qвращ3

q3(n+ m−7)

≠

k(T ) =

N V

пост

кол

exp

−

q3m−6q3n−6

пост

вращ

кол кол

Сравнивая (25.32.а) и (25.32.б), находим выражение для оценки стерического фактора:

	q	кол		5
P =		кол	.
P =			.

qвращ

Применение ТАК к мономолекулярным и тримолекулярным реакциям рассмотрено в примерах 25-3 и 25-2.

В термодинамическом подходе константу равновесия в уравнении Эйринга (25.23) выражают с помощью обычных термодинамических соотношений через стандартные термодинамические функции образования активированного комплекса – энтропию, энтальпию и энергию Гиббса1. Рассмотрим сначала реакции в газовой фазе. Константу скорости удобно связать c константой равновесия, выраженной через давления. Последняя константа, как известно, связана с изменением энергии Гиббса в реакции образования активированного комплекса:

∆G

≠

∆S

≠

∆H

≠

≠ = exp

−

= exp

exp

−

Для мономолекулярной реакции, в которой образование активированного комплекса происходит без изменения числа частиц, Kc≠ = K ≠p и константа скорости выражается следующим образом:

kBT

∆G ≠

kBT

∆S ≠

∆H ≠

k(T ) =

exp

−

exp

−

1 В приведенных ниже формулах значок «°», обозначающий стандартное состояние, опущен.

Г л а в а 5. Химическая кинетика

371

Энтальпию активации можно связать с опытной энергией активации, если воспользоваться определением (20.15) и уравнением Гиббса– Гельмгольца (5.9):

−

∆G

≠

2 d ln k

2 d lnT

≠

Eоп = RT

= RT

+ RT

= ∆H

+ RT .

В бимолекулярной реакции из двух молекул газа образуется одна молекула активированного комплекса, поэтому

Kc≠ =

K p≠ ,

где p° = 1 бар = 100 кПа.

Константа равновесия имеет вид:

kBT

∆G ≠

k(T ) =

exp

−

kBT

∆S ≠

∆H ≠ .

exp

−

Для бимолекулярных реакций энтропийный фактор exp(∆S≠/R) интерпретируют как стерический множитель P из теории активных столкновений. Энтальпия активации связана с опытной энергией активации следующим образом:

∆H ≠ = Eоп − 2RT .

(25.36)

(25.37)

(25.38)

(25.39)

Для реакций в растворах константу равновесия Kc≠ выражают через энергию Гельмгольца образования активированного комплекса:

kBT

∆F ≠

kBT

∆S ≠

∆U ≠

exp

k(T ) = h

−

(25.40)

Поскольку реакции в растворах почти не сопровождаются измене-

нием объема, то ∆G ≠≈ ∆F ≠ , а ∆H ≠≈ ∆U ≠, поэтому для расчета термодинамических функций активированного комплекса можно пользоваться формулами (25.35) и (25.36), справедливыми для мономолекулярных реакций в газовой фазе. При этом надо иметь в виду, что стандартные состояния для реакций в газовой фазе и в растворе отличаются друг от друга.

372	Г л а в а 5. Химическая кинетика

ПРИМЕРЫ

Пример 25-1. Константа скорости бимолекулярной реакции

2NO2 → 2NO + O2

при 627 °С равна 1.81 103 см3 моль–1 с–1. Вычислите истинную энергию активации и долю активных молекул, если радиус молекулы NO2 можно принять равным 3.55 Å, а стерический множитель для этой реакции равен 0.019.

Решение. При расчете будем опираться на теорию активных столк-

новений (формулы (25.5), (25.8)):

−

k(T )

exp

1 / 2

8P N

πRT

=			1.81 10−3					= 2.20	10−10.
		23		−10		2	3.14 8.31 900 1 / 2

	8 0.019 6.02 10		(3.55 10		)
							0.046

Это число представляет собой долю активных молекул.

При расчетах констант скорости с использованием различных теорий химической кинетики необходимо очень аккуратно обращаться с размерностями. Проще всего приводить все единицы к системе СИ.

Истинную энергию активации легко вычислить через долю активных молекул:

EA = −RT ln(2.20 10−10 ) =8.31 900 22.2 =166000 Дж моль–1 = 166 кДж моль–1.

Пример 25-2. Используя теорию активированного комплекса, определите температурную зависимость константы скорости тримолекулярной реакции

2NO + Cl2 = 2NOCl

при температурах, близких к комнатной. Найдите связь между опытной и истинной энергиями активации.

Решение. Согласно статистическому вариант ТАК, константа скорости равна (формула (25.24)):

	kBT		Q	≠				E	≠
k(T ) =		(N AV )2				exp	−		0	.
	h		QNO2 QCl
					2			RT

В суммах по состояниям активированного комплекса и реагентов мы не будем учитывать колебательные и электронные степени свободы,

Г л а в а 5. Химическая кинетика

373

т.к. при низких температурах колебательные суммы по состояниям близки к единице, а электронные – постоянны.

Температурные зависимости сумм по состояниям с учетом поступательного и вращательного движений имеют вид:

Q≠ = Qпост Qвращ ~ T 3/ 2 T 3/ 2 = T 3 ,

QNO = Qпост Qвращ ~ T 3/ 2 T = T 5 / 2 ,

QCl2 = Qпост Qвращ ~ T 3/ 2 T = T 5 / 2 .

Активированный комплекс (NO)2Cl2 – нелинейная молекула, поэтому его вращательная сумма по состояниям пропорциональна T 3/2.

Подставляя эти зависимости в выражение для константы скорости, находим:

T 3

E0≠

−7 / 2

E0≠

k(T ) ~ T

exp −

= T

exp −

5 / 2

) T

Мы видим, что тримолекулярные реакции характеризуются довольно необычной зависимостью константы скорости от температуры. При определенных условиях константа скорости может даже убывать с ростом температуры за счет предэкспоненциального множителя!

Опытная энергия активации этой реакции равна:

Пример 25-3. Используя статистический вариант теории активированного комплекса, получите выражение для константы скорости мономолекулярной реакции.

Решение. Для мономолекулярной реакции A A≠ → продукты

константа скорости, согласно (25.24), имеет вид:

	kBT	Q ≠			E0≠
k(T ) =			exp	−		.
k(T ) =	h	QA	exp	−		.
	h	QA			RT

Активированный комплекс в мономолекулярной реакции представляет собой возбужденную молекулу реагента. Поступательные суммы

реагента A и комплекса A≠ одинаковы (масса – одна и та же). Если предположить, что реакция происходит без электронного возбуждения, то и электронные суммы по состояниям одинаковы. Если считать, что при возбуждении строение молекулы реагента изменяется не очень

<<< < Предыдущая 24 25 26 27 28 29 30 31 32 33 34 35 3637 / 4837 38 39 40 41 42 43 44 45 46 47 48 > Следующая >>>

Соседние файлы в папке 7 семестр

#
02.01.2023721.17 Кб28Лекции.docx
#
02.01.20233.78 Mб29Методичка - Химическая кинетика.pdf
#
02.01.20235.51 Mб84Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с.pdf