
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf
|
|
Г л а в а 5. Химическая кинетика |
345 |
||
|
3 |
|
|
|
|
-1 |
2 |
|
|
|
|
с |
|
|
|
|
|
-1 |
|
|
|
|
|
мольл |
|
|
|
|
|
, |
1 |
|
|
|
|
5 |
|
|
|
|
|
r 10 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
||||
|
|
|
r / [S] 104, c-1 |
|
|
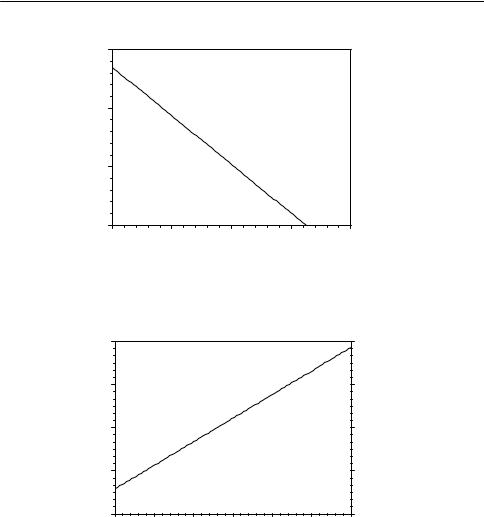
23-18. Найдите константу Михаэлиса и максимальную скорость гидролиза карбобензилоксиглицилфенилаланина под действием карбоксипептидазы по следующим кинетическим данным:
|
12 |
|
|
|
|
|
|
с |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
лмоль |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
10 |
3 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
0 |
||||||
|
|
|
[S]−1, л моль−1 |
|
|
||
23-19. Определите значения константы Михаэлиса и максимальной скорости для гидролиза метилового эфира N-ацетил-L-валина, катализируемого α-химотрипсином. Экспериментальные данные о зависимости начальной скорости от концентрации субстрата:
[S]0, M |
r0 106, М с–1 |
0.200 |
4.57 |
0.124 |
3.83 |
0.124 |
3.84 |
0.091 |
3.33 |
0.091 |
3.31 |
0.071 |
2.97 |
0.071 |
2.93 |
0.060 |
2.67 |
0.060 |
2.74 |

346 |
Г л а в а 5. Химическая кинетика |
23-20. Определите значения константы Михаэлиса и максимальной скорости для гидролиза метилового эфира N-бензоил-L-аминомасляной кислоты, катализируемого α-химотрипсином. Экспериментальные данные о зависимости начальной скорости от концентрации субстрата:
[S]0 103, M |
r0 107, М с–1 |
2.24 |
4.25 |
2.24 |
4.31 |
1.49 |
3.52 |
1.49 |
3.60 |
1.12 |
3.10 |
1.12 |
3.12 |
0.90 |
2.71 |
0.90 |
2.77 |
0.75 |
2.45 |
0.75 |
2.40 |
23-21. Определите значения константы Михаэлиса и максимальной скорости для гидролиза метилового эфира N-ацетил-L-норвалина, катализируемого α-химотрипсином. Экспериментальные данные о зависимости начальной скорости от концентрации субстрата:
|
[S]0 102, M |
|
r0 107, М с–1 |
|
|
4.00 |
|
9.70 |
|
|
4.00 |
|
10.0 |
|
|
2.00 |
|
7.77 |
|
|
2.00 |
|
7.85 |
|
|
1.33 |
|
6.51 |
|
|
1.33 |
|
6.41 |
|
|
1.00 |
|
5.50 |
|
|
1.00 |
|
5.51 |
|
|
0.80 |
|
4.80 |
|
|
0.80 |
|
4.76 |
|
23-22. Рассчитайте концентрацию |
неконкурентного ингибитора I |
|||
(KI = 2.9 10–4 моль л–1), необходимую для 90%-ного подавления ферментативной реакции.
23-23. В некоторых случаях кинетические исследования ферментативных реакций проводят в условиях избытка фермента. Выведите уравнение Михаэлиса–Ментен, описывающее зависимость начальной скорости ферментативной реакции от начальных концентраций фермента и субстрата в системе
E + S |
k1 |
ES |
k2 |
E + P |
|
|
|||
k-1 |
|
|||
|
|
|
|

Г л а в а 5. Химическая кинетика |
347 |
при условии, что концентрация фермента намного больше концентрации субстрата.
23-24. Рассмотрите механизм ферментативного катализа с двумя промежуточными комплексами:
E + S |
k1 |
ES |
k2 |
EP |
k3 |
E + P . |
|
|
|
||||
k-1 |
k-2 |
|
||||
|
|
|
|
|
Используя метод квазистационарных концентраций и уравнение материального баланса, покажите, что скорость реакции описывается уравнением типа Михаэлиса–Ментен (23.14). Найдите выражения для эффективной максимальной скорости и эффективной константы Михаэлиса через константы скорости отдельных стадий.
23-25. Запишите уравнения конкурентного и неконкурентного ингибирования в координатах Лайнуивера–Берка. Представьте эти уравнения в графическом виде для трех разных начальных концентраций ингибитора (включая [I]0 = 0). Объясните, как можно определить константу ингибирования.
23-26. Запишите уравнения конкурентного и неконкурентного ингибирования в координатах r0 – r0/[S]0. Представьте эти уравнения в графическом виде для трех разных начальных концентраций ингибитора (включая [I]0 = 0). Объясните, как можно определить константу ингибирования.
23-27. Рассмотрите схему неконкурентного ингибирования с разными константами диссоциации комплексов:
E + S |
|
k1 |
|
ES |
k2 |
E + P , |
|||
|
k-1 |
|
|||||||
|
|
|
|
|
|
|
|
||
E + I |
|
|
EI , |
|
K1 |
= [E][I] / [EI] , |
|||
|
|
|
|
||||||
|
|
||||||||
ES + I |
|
|
|
ESI , |
K2 |
= [ES][I] / [ESI] .. |
|||
|
|
|
|||||||
|
|
|
|||||||
Используя квазистационарное приближение для ES и квазиравновесное приближение для EI и ESI, найдите начальную скорость реакции. Как связаны максимальная скорость реакции и константа Михаэлиса с соответствующими величинами для неингибируемой реакции?
23-28. Рассмотрите схему субстратного ингибирования:
E + S |
|
k1 |
ES |
k2 |
E + P , |
|
|
k-1 |
|
||||
ES + S |
|
|
|
KS = [ES][S] / [SES] . |
||
|
|
SES , |
||||
|
|
|||||
|
|
|||||

348 |
Г л а в а 5. Химическая кинетика |
Используя квазистационарное приближение для ES и квазиравновесное приближение для SES, найдите скорость реакции и изобразите график зависимости скорости от концентрации субстрата.
23-29. Антибиотик пенициллин инактивируется ферментом пенициллиназой, выделяемым некоторыми бактериями. Пусть добавление 3 мкмоль антибиотика вызывает выделение 2.0 10–6 мкмоль фермента в 1.00 мл бактериальной суспензии. Считая, что данная реакция описывается схемой Михаэлиса–Ментен
E + S |
k1 |
ES |
k2 |
E + P |
|
|
|||
k-1 |
|
|||
|
|
|
|
с константами KM = 5.0 10–5 М и k2 = 2.0 103 с–1, рассчитайте время, необходимое для инактивации 50% антибиотика.
23-30. Простейшая схема бесконкурентного ингибирования описывается уравнениями:
E + S |
k1 |
|
ES |
k2 |
E + P |
|
k-1 |
|
|||||
|
|
|
|
|
||
ES + I |
|
ESI |
|
K = [ES][I] / ([ESI]). |
||
|
|
|||||
|
|
|||||
Используя квазистационарное приближение для ES и квазиравновесное приближение для ESI, найдите начальную скорость реакции r0. Как связаны максимальная скорость реакции и константа Михаэлиса с соответствующими величинами для неингибируемой реакции? На одном графике изобразите в двойных обратных координатах зависимость скорости от концентрации субстрата для ингибируемой и неингибируемой реакции.
23-31. При добавлении конкурентного ингибитора в ферментативную систему, подчиняющуюся схеме Михаэлиса–Ментен (KM = 2.5 10–3 моль л–1), скорость реакции уменьшилась на 60%. Концентрация субстрата равна 3.0 10–3 моль л–1, концентрация ингибитора 3.0 10–4 моль л–1. При какой концентрации субстрата скорость реакции составит 30% от исходной при тойжеконцентрацииингибитора?
23-32. При добавлении неконкурентного ингибитора в ферментативную систему, подчиняющуюся схеме Михаэлиса–Ментен (KM = = 3.0 10–3 моль л–1), скорость реакции уменьшилась на 70%. Концентрация субстрата равна 2.5 10–3 моль л–1, концентрация ингибитора 5.0 10–4 моль л–1. При какой концентрации ингибитора скорость реакции составит 35% от исходной?
23-33. α-Кетоглутарат – конкурентный ингибитор реакции окисления N-метил-L-глутамата, катализируемой N-метилглутамат-дегидрогена-
Г л а в а 5. Химическая кинетика |
349 |
зой. Определите константу диссоциации комплекса фермент-ингиби- тор. Экспериментальные данные о влиянии α-кетоглутарата на кинетику окисления N-метил-L-глутамата:
[α-кетоглутарат] 104, M |
[S]0 104, M |
r0 106, М мин–1 |
|
1.00 |
1.67 |
0 |
0.625 |
1.43 |
0.500 |
1.33 |
|
|
0.417 |
1.25 |
|
0.264 |
1.00 |
|
1.67 |
1.67 |
|
1.00 |
1.43 |
0.6 |
0.625 |
1.18 |
|
0.500 |
1.04 |
|
0.330 |
0.83 |
|
5.00 |
1.56 |
|
1.67 |
1.00 |
3.0 |
1.00 |
0.77 |
|
0.667 |
0.57 |
|
0.500 |
0.45 |
23-34. Бензоат 1,2,5-триметилпиперидола-4 (β-изомер) ингибирует гидролиз бутирилхолина, катализируемый холинэстеразой. Определите тип ингибирования и рассчитайте константу диссоциации комплекса фер- мент-ингибитор. Экспериментальные данные:
[I] 105, M |
[S]0 104, M |
r, усл. ед. |
|
10.00 |
5.55 |
|
2.50 |
4.45 |
0 |
0.91 |
2.94 |
|
0.50 |
2.09 |
|
10.00 |
4.77 |
|
2.50 |
3.78 |
0.5 |
0.91 |
2.56 |
|
0.50 |
1.79 |
|
10.00 |
4.00 |
|
2.50 |
3.18 |
1.0 |
0.91 |
2.16 |
|
0.50 |
1.49 |
|
10.00 |
2.86 |
|
2.50 |
2.28 |
2.0 |
0.91 |
1.52 |
|
0.50 |
1.06 |
|
10.00 |
2.38 |
|
2.50 |
1.85 |
3.0 |
0.91 |
1.24 |
|
0.50 |
0.87 |

350 |
Г л а в а 5. Химическая кинетика |
23-35. Известны два простых механизма ферментативного катализа, включающие образование фермент-субстратного комплекса:
1) схема Михаэлиса (реакционноспособный комплекс): E + S ES → E + P;
2) схема Анри (инертный комплекс):
E + S ES; E + S → P.
Обе схемы приводят к одной и той же зависимости начальной скорости от начальной концентрации субстрата. Различить эти схемы можно только по кинетическим кривым. Определите зависимости концентрации продукта от времени для механизмов Михаэлиса и Анри. Изобразите качественно эти зависимости на одном графике.
23-36. Основываясь на уравнении (23.25), рассмотрите кинетику гетерогенной реакции изомеризации в случае слабой адсорбции субстрата и сильной адсорбции продукта. Какой порядок имеет реакция в этом случае? Найдите выражение для экспериментально наблюдаемой энергии активации.
23-37. При каких условиях двухсубстратная реакция, рассмотренная в примере 23-5а, имеет общий нулевой порядок?
23-38. Каталитическое окисление CO на однородной поверхности Pd протекает следующим образом:
CO(адс.) + 1/2 O2(адс.) |
k1 |
CO2(адс.) |
k2 |
CO2(г.). |
|
|
|||
k-1 |
|
|||
|
|
|
|
Равновесие на поверхности устанавливается быстро. Вторая стадия – медленная. Используя уравнение Ленгмюра для многокомпонентной адсорбции (23.22), выведите формулу для зависимости скорости реакции образования газообразного CO2 от парциальных давлений всех участников реакции.
§ 24. Фотохимические реакции
|
Многие химические реакции происходят под действием электро- |
||
|
магнитного излучения. Как мы видели в § 15, различные виды излуче- |
||
|
ния способны активизировать разные виды движения в молекуле – |
||
|
вращательное, колебательное, электронное. Энергия одного кванта из- |
||
|
лучения связана с длиной волны λ соотношением: |
||
(24.1.а) |
E = hν = |
hc |
, |
|
|||
|
|
λ |
|
где ν – частота излучения, h – постоянная Планка, c – скорость света. Один моль квантов света иногда называют эйнштейном. В спектроско-
Г л а в а 5. Химическая кинетика |
351 |
пии и в атомной физике в качестве единиц энергии используют «обратные сантиметры», см–1. Энергия излучения, выраженная в обратных сантиметрах, связана с длиной волны соотношением:
E = |
1 |
. |
(24.1.б) |
|
|||
|
λ |
|
|
Характеристики основных видов электромагнитного излучения приведены в таблице П-14 в Приложении III. Для возбуждения большинства фотохимических реакций используют видимое или УФ излучение.
Согласно первому закону фотохимии (Гротгус (1817), Дрепер (1830)), фотохимическое превращение может происходить только под действием того света, который поглощается веществом. Второй закон фотохимии сформулировали Штарк и Эйнштейн (1912): каждый поглощенный фотон вызывает фотохимическое возбуждение одной молекулы. Этот закон нарушается в сильных световых полях, где происходят многоквантовые процессы и одна молекула может поглотить несколько квантов излучения.
При поглощении видимого или УФ света молекула переходит в возбужденное электронное состояние:
A + hν → A*.
Возбужденная молекула может испытывать последующие превра-
щения – первичные фотофизические и фотохимические процессы.
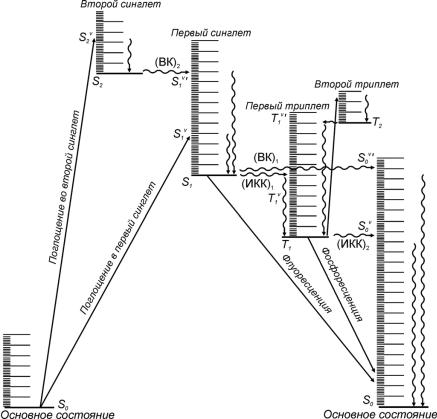
Первичные фотофизические процессы (рис. 24.1):
1.Колебательная релаксация – безызлучательный процесс, который приводит к рассеиванию (диссипации) колебательной энергии по внут-
ренним степеням свободы в данном электронном состоянии. Колебательная релаксация происходит за время 10–11 – 10–12 с.
2.Флуоресценция – излучательный переход между состояниями одной и той же мультиплетности, например синглет-синглет. При испускании света происходит переход в исходное электронное состояние:
A* → A + hνf.
Частота испускаемого света меньше или равна частоте поглощаемого в первичном процессе света: νf ≤ ν. Время жизни первого синглетно-
го состояния, из которого происходит флуоресценция, составляет обычно 10–8 – 10–9 с.
3.Внутренняя конверсия – безызлучательный переход между электронными состояниями одинаковой мультиплетности.
4.Интеркомбинационная конверсия – безызлучательный переход между электронными состояниями разной мультиплетности, например синглет – триплет.
352 |
Г л а в а 5. Химическая кинетика |
5. Фосфоресценция – излучательный переход между состояниями разной мультиплетности. Испускание света происходит с некоторой задержкой по времени, которая необходима для того, чтобы молекула за счет безызлучательных процессов перешла в триплетное состояние. Триплетные состояния живут гораздо дольше, чем синглетные: время жизни составляет 10–6 – 102 с.
Правило Каша: флуоресценция (фосфоресценция) происходит с низшего возбужденного уровня (первого синглетного или низшего триплетного).
Рис. 24.1 |
Возбужденные состояния типичной органической молекулы и первичные |
фотофизические процессы. S – синглетные состояния, T – триплетные. |
|
|
Излучательные переходы обозначены прямыми стрелками, |
|
безызлучательные – волнистыми. ВК – внутренняя конверсия, |
|
ИКК – интеркомбинационная конверсия. Буквы v и v’ обозначают |
|
колебательно возбужденные уровни |
Первичные фотохимические процессы
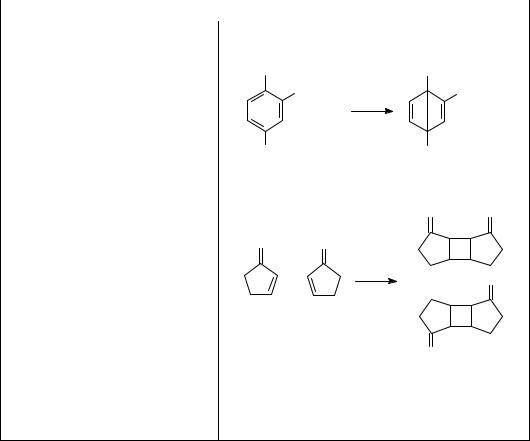
Поглощение света может привести к разнообразным химическим превращениям электронно-возбужденной молекулы. Основные типы первичных фотохимических процессов перечислены в табл. 24.1.
Г л а в а 5. Химическая кинетика |
|
|
353 |
||
Первичные фотохимические реакции |
Таблица 24.1 |
||||
|
|
|
|
|
|
Название |
|
Пример |
|
|
|
Диссоциация на радикалы |
|
RCHO → R + CHO |
|
|
|
Диссоциация на молекулы |
|
RCHO → RH + CO |
|
|
|
Внутримолекулярная перегруппи- |
C(CH3)3 |
C(CH3)3 |
|||
ровка |
C(CH3)3 |
C(CH3)3 |
|||
|
C(CH3)3 |
C(CH3)3 |
|||
|
|
|
|||
Изомеризация |
цис-RCH=CHR → транс-RCH=CHR |
||||
Отрыв атома водорода |
(C6H5)2CO + RH → (C6H5)2COH + R |
||||
Димеризация |
|
O |
|
O |
|
|
O |
O |
|
|
|
|
+ |
|
+ O |
||
|
O |
Ионизация |
A* → A+ + e |
Внешний перенос электрона |
[Fe(CN)6]4– → [Fe(CN)6]3– + e– |
Внутренний перенос электрона |
Реакции типа DBA → D+BA– |
|
(D – донор, B – мостик, A – акцептор электрона) |
Эффективность фотохимической реакции характеризуют квантовым выходом, который равен отношению числа прореагировавших молекул к числу поглощенных фотонов:
ϕ = |
N(молекул) |
. |
(24.2) |
|
|||
|
N (hν) |
|
|
Все фотохимические реакции по значению квантового выхода можно разбить на три группы.
1.ϕ = 1, например образование бромциклогексана или перекиси водорода.
2.ϕ < 1, например разложение ацетона (см. задачу 24-4) или аммиака. Такое значение квантового выхода свидетельствует о том, что в результате первичного процесса образуются устойчивые молекулы, и фотохимическая реакция на этом заканчивается.
3.Если же первичная реакция приводит к появлению реакционноспособных частиц, например, свободных радикалов, то возможны вторичные процессы – цепные реакции или рекомбинация. В этом случае экспериментальные значения квантового выхода могут значительно
