
Савёлова Методы решения некорректных задач 2012
.pdf
где
S(α) (2l
l 0
соответственно
M 
 fNP (g) fNP (g)
fNP (g) fNP (g)

|
Q |
|
2 |
|
|
1) |
l |
|
|
, |
|
|
|
|
|||
|
2l 1 |
|
|
||
|
|
|
L |
|
|
2 ζ2 (N ) (2l 1). |
(8.40) |
||||
L2 |
|
l 0 |
|
|
|
|
|
|
|
||
Из неравенств (8.39), (8.40) получаем следующее утверждение.
Утверждение 8.6 (достаточные условия устойчивости ядер-
ных и проекционных оценок в L2 и L1 ). Пусть для ядерных оце-
нок fNk (g) (8.34) и проекционных оценок fNP (g) (8.35) выполне-
ны условия а–г относительно погрешностей элементов выборки.
Тогда оценки |
f k (g) устойчивы в |
L |
и L при |
ζ2 (N)S(α) 0, |
|||||
|
N |
|
|
|
2 |
1 |
|
|
|
N , α |
0 , оценки |
P |
(g) |
устойчивы в |
L |
и L |
при |
||
f |
N |
||||||||
|
|
|
|
|
|
2 |
1 |
||
ζ2 (N ) 12 L(2L 1) 0, N , L .
8.7. Оценка точности ядерных методов для зависимых
ориентировок
По выборке из зависимых между собой вращений g1,..., gN , от-
вечающей плотности распределения f g , рассмотрим ядерную оценку [27, 28]
181
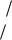
|
|
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
1 |
|
π |
|
|
|
t |
|
|
|
fNk g |
|
Ci q gi 1g , q t 0, |
|
|
q t sin2 |
dt 1. (8.41) |
|||||||||||||||||||
|
|
π π |
|
||||||||||||||||||||||
|
|
|
|
|
N i 1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
(8.41) |
ядро |
имеет |
|
|
вид |
q t Ql χl t , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
χ |
|
t |
sin l 1 2 t |
, C 0 |
|
– веса, отвечающие размеру зерна с |
|||||||||||||||||||
l |
|
||||||||||||||||||||||||
|
|
|
|
sin |
t 2 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ориентацией |
gi , |
|
Ci |
1, |
проекционная оценка получается из |
||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i 1 N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(8.41) при Ql |
1, |
l L; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
l L. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Оценка (8.41) может быть преобразована к виду |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ql |
|
|
|
l |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
fNk g |
|
ClmnTl mn g , |
(8.42) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
2l 1 mn l |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Cmn – оценки коэффициентов Cmn : |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2l 1 |
|
|
N |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Clmn |
|
CiTl |
mn gi . |
(8.43) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
i 1 |
|
|
|
|
|
|
||||
Из выражений (8.42), (8.43) вычисляем математическое ожида-
ние
|
Ql |
l |
|
fN g MfNk g |
ClmnTl mn g . (8.44) |
||
|
|||
l 0 |
2l 1 m,n l |
||
182 |
|
|
|

Из (8.44) находим смещение оценки (8.42), (8.43):
|
|
|
Q |
|
l |
sN g f g fN g 1 |
|
l |
|
ClmnTl mn g . (8.45) |
|
|
|||||
l 0 |
|
|
2l 1 m,n l |
||
Из уравнения (8.45) видим, что смещение оценки (8.42) не зави-
сит от зависимости ориентаций и распределения размеров зерен.
Дисперсия оценки (8.42), (8.43) имеет вид
DfNk
l1 ,l2 0 l1 l2
|
|
|
|
|
Q |
|
2 |
l |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
g |
|
|
l |
|
|
DClmn |
|
Tl mn g |
|
|
|
|||||
|
|
|
|
|||||||||||||
|
|
|
l 0 |
2l 1 |
m,n l |
|
|
|
|
|
|
|
||||
Q |
|
|
Q |
|
|
l1 |
l2 |
|
|
|
|
|
|
|
||
l1 |
|
|
|
l2 |
|
|
|
cov Clm1 1n1 Clm2 2n2 |
|
|||||||
2l 1 2l |
1 |
|
||||||||||||||
m1 |
,n1 l1 |
m2 ,n2 l2 |
|
|
|
|
|
|
|
|||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
T m1n1 g T m2n2 |
g . |
|
|
|
(8.46) |
||||||
|
|
|
|
|
|
l |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
В соотношении (8.46) имеем дисперсии оценок (8.43) и их кова-
риации
|
|
2l |
1 2 |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
DClmn |
|
|
|
CiC j cov Tl mn gi Tl mn g j , |
(8.47) |
||||||||||||||
N |
2 |
||||||||||||||||||
|
|
|
i, j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2l 1 2l |
|
|
1 N |
|
|||||||
|
cov Clm1 1n1 Clm2 2n2 |
|
1 |
|
|
|
|
2 |
|
CiC j |
|
||||||||
|
|
|
N |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
cov Tl |
m1n1 |
|
|
|
g j . |
|
||||||||||
|
|
|
gi Tl |
m2n2 |
(8.48) |
||||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|||
183
Дисперсия оценок коэффициентов (8.47) имеет вид
|
mn |
|
|
2l |
|
2 |
|
N |
2 |
2l |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Ci |
C l,l,l , m, m, 2m C l,l,l , n, n, 2n |
||||||||||||||
DCl |
|
|
|
|
|
||||||||||||||||||
|
N |
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
l 0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
Cl2m2n |
|
|
|
|
CiC j cov Tl mn gi Tl mn g j |
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2l 1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
i, j 1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mn |
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Cl |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(8.49) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2l 1 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где C l,l,l , m, m, 2m – коэффициенты Клебша–Гордана.
Ковариации (8.48) вычисляются следующим образом:
|
|
|
cov Clm1n1 , Clm2n2 2l1 |
1 2l2 1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
2 |
|
|
N 2 |
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
N |
|
|
|
l1 l2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ci |
C |
l1,l2 ,l , m1, m2 , m1 m2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
l |
l1 l2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
N |
|
||
C l1,l2 ,l , n1, n2 |
, n1 n2 Clm1 m2 ,n1 n2l |
|
CiC j |
||||||||||||||||||
|
|
|
|||||||||||||||||||
2l 1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
||||
cov Tl m1n1 |
gi Tl m2n2 g j |
Clm1n1 Clm2n2 |
|
||||||||||||||||||
|
|
|
|
|
|
. (8.50) |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
2 |
|
|
|
1 |
2 |
|
2l1 1 2l2 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Из соотношений (8.49), (8.50) легко найти, что если ориентации g1,..., gN зависимы таким образом: имеется K групп ориентиро-
вок количеством N1, N2 ,..., NK , N2 < N1 элементов из первых N1 ,
184

NK < NK 1 элементов из предыдущих NK 1 элементов, где
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N j N , элементы внутри групп независимы между собой, то |
||||||||||||||||||||||||||||||||||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l 1 |
2 |
K |
|
|
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
mn |
|
|
|
|
|
Ni |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
DCl |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
N |
|
|
|
|
C l,l,l , m, m, 2m C l,l,l , n, n, 2n |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Clmn |
2 |
|
|
|
|
|
|
|
|
|
|
2l |
1 |
|
|
2l |
|
1 |
K |
|
|
|||||||||||||
Cl2m2nl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ni |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
2l 1 |
|
|
2l 1 |
2 |
|
|
|
|
|
|
N |
2 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
l1 l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, n1 n2 |
||||||||||
|
|
C l1,l2 ,l , m1, m2 , m1 m2 C l1 |
,l2 ,l , n1, n2 |
|||||||||||||||||||||||||||||||||||||||||||
|
l |
|
l1 l2 |
|
|
m1 m2 ,n1 n2l |
|
|
|
|
|
m1n1 |
|
|
m2n2 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
Cl |
|
|
|
|
|
Cl1 |
Cl2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(8.51) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l1 1 2l2 1 |
|
|
|
|
|
|||||||||||||||
Из уравнений (8.45)–(8.46) получаем оценку точности ядерной |
||||||||||||||||||||||||||||||||||||||||||||||
оценки (8.42), (8.43) в норме L2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
M |
|
f g f k |
g |
|
|
|
2 |
|
2 |
2 , |
|
|
|
(8.52) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
L2 |
1 |
|
|
|
2 |
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
2 |
l |
|
|
1 |
|
|
|
Clmn |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
12 1 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l |
1 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
|
|
|
|
2l 1 |
|
m,n l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
есть влияние смещения оценки sN ,
|
|
Q |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2l 1 |
|
N |
||||
22 |
l |
|
|
|
|
|
|
|
|
CiC j |
|
|
|
|
|
2 |
|
|
|||||
l 0 |
2l 1 |
|
|
N |
|
|
|
i, j 1 |
|||
влияние дисперсии оценки |
|
fNk g . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
185 |
l |
|
|
|
cov Tl |
|
|
mn g j – |
mn gi Tl |
|||
m,n l |
|
|
|
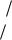
Для центральных функций на SO(3) имеем разложение по ха-
рактерам представлений
|
|
|
1 |
π |
|
|
|
t |
|
f t Cl χl t , |
Cl |
|
f t χl t sin2 |
dt, |
|||||
π π |
|
||||||||
l 0 |
|
|
|
2 |
(8.53) |
||||
|
|
sin l |
1 2 |
t |
|
|
|||
χl t |
. |
|
|||||||
sin t |
2 |
|
|
||||||
|
|
|
|
|
|
||||
Ядерная оценка по выборке t1,..., tN из зависимых элементов
имеет вид
|
Q |
|
||
fNk t |
l |
|
Cl χl t , |
|
2l 1 |
||||
l 0 |
|
|||
|
1 |
N |
|
χl ti . (8.54) |
|||
Cl |
|||
|
|||
|
N i 1 |
||
Смещение оценки (8.54) вычисляется по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|||||||
|
|
|
sN |
|
f t MfNk t |
1 |
|
|
l |
|
Cl χl |
t . |
|
(8.55) |
|||||||||||||||||||||||
|
|
|
|
2l |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
|
|
1 |
|
|
|
|
|||||||||
Дисперсия оценки (8.54) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
N |
|
|
|
|
|
Ql |
Ql |
|
1 |
|
|
|
|
N |
|
|
|
|
|
j |
|
|
|
|
l1 |
i |
l2 j |
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
2 |
|
|
i |
|
|
|
|
||||||||||||||||
Df |
k |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C C cov χ |
|
t χ t |
. (8.56) |
|||||||||||||||
|
l1 ,l2 0 |
|
2l 1 2l 1 N |
|
|
|
i, j 1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из выражений (8.53)–(8.56) имеем оценку точности |
f k |
t |
в L |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
2 |
|
|
|
2 |
M |
|
f t f k t |
|
|
|
2 |
|
2 |
2 |
, |
|
|
(8.57) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
L2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ql |
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
C |
, |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2l |
1 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
N |
|
|
|
|
|
|
Q |
|
|
|
2 |
cov χl |
|
|
|
t j , |
|
|||||||||||||
|
|
22 |
|
|
|
|
CiC j |
|
|
|
|
|
l |
|
|
|
|
ti , χl |
|
||||||||||||||||||
|
|
N |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
i, j 1 |
l 0 |
2l 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
186 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2l 2
D l ti Cl Cl .
l 0
При наличии симметрии кристаллита имеет место представле-
ние ФРО
|
|
|
|
|
|
|
|
|
|
|
l |
|
1 |
|
|
M |
|
|||||
|
|
|
f (g) sim Cmnl |
|
Tmnl gBj g , |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
l 0 m,n l |
|
M j 1 |
|
|||||||||||
где gB |
, j =1,…, M – подгруппа симметрии кристаллита. |
|
||||||||||||||||||||
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае ядерная оценка ФРО имеет вид |
|
|||||||||||||||||||||
|
|
|
|
|
Ql |
|
|
l |
|
1 |
|
M |
|
|||||||||
|
|
|
fNk (g) |
|
Cmnl |
|
|
Tmnl gBj g , |
|
|||||||||||||
|
|
|
2l |
|
M |
|
|
|||||||||||||||
|
|
|
|
l 0 |
1 m,n l |
|
|
|
|
j 1 |
|
|||||||||||
где оценка коэффициентов вычисляется по формуле |
|
|||||||||||||||||||||
|
|
|
|
Cmnl |
|
|
|
|
N |
M |
|
|
|
|
|
|
|
|||||
|
|
|
|
2l 1 Tmnl gBj g . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
NM i 1 |
j 1 |
|
|
|
|
|
|
||||||
Заметим, |
что |
при |
|
наличии |
|
|
|
симметрии |
величина |
|||||||||||||
2 M |
|
f (g) f k (g) |
|
|
|
2 не меняется. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
N |
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.8. Численные результаты
8.8.1. Вычисление точности ядерных и проекционных методов по набору из независимых ориентаций
В [27] рассматривается обобщение метода Розенблатта–Парзена на группу SO(3) c учетом инвариантной меры dg . В качестве оценки плотности берется величина
187

|
1 |
|
N |
|
φ φi |
|
|
cos θ cos θi |
|
fN* g |
|
q1 |
|
q2 |
|
|
|||
N hN |
3 |
|
hN |
||||||
|
|
i 1 |
|
hN |
|
|
|||
|
|
|
|
|
|
ψ ψ |
i |
|
|
|
|
|
|
|
||
|
|
|
q3 |
|
|
|
|
|
|
|
|
|
(8.58) |
|||
|
|
|
hN |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
по выборке g1 φ1,θi , ψi , ... , gN |
|
φN ,θN , ψN , где, в частно- |
||||||||||||||
сти, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
φ2 |
|
|
|
q1 φ |
2π π |
|
|
|
|
|
||||||||||
|
|
exp |
|
|
, |
|||||||||||
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ψ2 |
|
|
|
|
|
|
q3 ψ 2π π |
|
|
|
φ, ψ π, |
||||||||||||
|
exp |
|
|
, -π |
||||||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
cos2 θ |
|
|
q2 θ |
2π 1 |
|
|
|||||
|
exp |
|
|
, |
||||
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
1 cosθ 1, |
|
0 θ π. |
(8.59) |
||||||||||
С учетом инвариантной меры на SO(3) ЦНР может быть записано |
||||||||||||||
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F t dt 2l 1 exp l l 1 ε2 |
|
|||||||||||||
|
|
|
l o |
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
sin l |
|
|
|
t |
1 |
|
|
t |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
sin |
2 |
|
dt, π t π. |
(8.60) |
||||||
t |
|
π |
|
2 |
||||||||||
|
|
|
|
|
|
|||||||||
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|||||
Проекция на сферу S 2 |
|
в 3 |
ЦНР с учетом меры имеет вид [28] |
|||||||||||
f θ dθ 2l 1 exp l l 1 ε2
l o
188

P cosθ |
1 |
sin θdθ, 0 θ π, |
(8.61) |
|
|||
l |
2 |
|
|
|
|
|
где Pl z – полиномы Лежандра.
Методом статистических испытаний разыгрывалось N = 500,
3103 случайных вращений для приближения ЦНР с параметром
ε2 2 k , k 0, 2, 6 с показателем свертки n 6 (в некоторых
случаях использовалось также n 10, 18 ).
Строились гистограммы для дискретных значений ЦНР, дис-
кретных значений проекции на сферу и для функций |
F t |
(8.60), |
||
f θ |
(8.61) с шагом |
0,2 . Для вычисления функций |
F t и |
|
f θ |
использовалось |
суммирование ряда Фурье с |
количеством |
|
слагаемых l l |
, l |
|
|
ln δ0 |
, δ |
|
10 10 |
. Полученные результа- |
|
|
0 |
||||||
max |
max |
|
|
ε |
|
|
||
|
|
|
|
|
|
|
||
ты показаны на рис. 8.1–8.4, где даны гистограммы точного (штри-
ховая линия) и модельного (сплошная линия) распределений с па-
раметрами |
ε2 1 |
(случай а), |
ε2 1 4 (случай б), |
ε2 1 6 4 |
(случай в). |
Объем |
выборки |
N = 500 на рис. 8.1, 8.2, и N = 3000 – |
|
на рис. 8.3, 8.4. |
|
|
|
|
a |
б |
в |
Рис. 8.1. Гистограммы точного и модельного распределений F t (N=500)
189

a б в
Рис. 8.2. Гистограммы точного и модельного распределений f θ (N=500)
a б в
Рис. 8.3. Гистограммы точного и модельного распределений F(t) (N=3000)
a б в
Рис. 8.4. Гистограммы точного и модельного распределений f( ) (N=3000)
Для проверки гипотезы о совпадении распределений F(t), f( ) и
их дискретных аналогов использовался критерий χ 2 . Рассматрива-
лась величина
1 Pi |
Pi |
2 |
|
|
||
|
|
|
||||
Z N |
|
|
|
|
|
|
|
|
|
|
, |
(8.62) |
|
|
|
Pi |
|
|||
i 1 |
|
|
|
|
||
190 |
|
|
|
|
|
|
