Савёлова Методы решения некорректных задач 2012

на SO(3) при αii 0 . Кроме того, используя уравнение

получаем бесконечную дифференцируемость КНР.

Итак, мы можем вычислить НР с достаточно малой погрешно-

стью δ 10 4 10 3 . Точность вычисления НР другими методами будем рассматривать путем сравнения с методом суммирования

ряда Фурье.

Из соотношения (5.9) видно, что объем вычислений возрастает

во членов ряда Фурье необходимое для суммирования для получе-

ния КНР с заданной точностью. Данная ситуация возникает при аппроксимации острой текстуры с помощью НР.

Следовательно, можно дать заключение об эффективности вы-

числения НР путем суммирования ряда Фурье. Этот метод эффек-

тивен и может быть практически использован в случае достаточно больших значений параметров, когда количество членов ряда Фу-

рье невелико. В случае малых параметров НР метод неэффективен и неустойчив по причине необходимости суммирования большого числа членов ряда Фурье с приближенными коэффициентами.

Метод суммирования ряда Фурье применяется для вычисления

полюсных фигур с кристаллографическим направлением

h 001 , используя КНР в качестве ФРО для некоторого набора параметров. Значение lmax берется в соответствии с уравнением

(5.9). Результаты вычислений показаны на рис. 5.1 и 5.2. 121

α33 =0,009 при lmax 38. В обоих случаях относительная ошибка

вычисления ПФ 0,1 %. Вычисления проводились с помощью про-

граммного обеспечения Mathlab (http://www.mathroots.com) на пер-

сональном компьютере с процессором Pentium 4. В первом случае время вычисления равно 11,8 с (рис. 5.1) и 124,6 с – во втором

(рис. 5.2).

122

5.2.2. Аналитическое приближение

Наиболее распространенная параметризация вращения – пара-

метризация углами Эйлера. Однако вращение также полностью

ξ1, ξ2 , ξ3 ωn1, ωn2 , ωn3 . При этом ω2 =ξ12 +ξ22 +ξ32 .

С помощью такой параметризации найдено аналитическое при-

ближение НР [6, 38, 58] в виде

матрица вида (5.5), ε – фиксированное число.

Условие совпадения распределения (5.10) с НР в точке макси-

мума позволяет однозначно найти ε :

ческая форма (5.10) имеет простое выражение

123

Асимптотическое приближение ПФ для ФРО вида (5.12) имеет вид

ветственно. Для приближенного вычисления ЦНР удобны форму-

лы, приведенные в приложении 3.

124

Для оценки точности метода аналитических приближений срав-

ним результат вычисления ПФ, полученный указанным способом с результатом расчета методом суммирования ряда Фурье, с помо-

щью RP-фактора.

Представим пример вычисления ПФ для КНР с теми же пара-

метрами, что и для рассмотренного метода суммирования ряда Фу-

рье. Вычисленные ПФ изображены на рис. 5.3 и 5.4. Точность вы-

числения ПФ согласно выражению (5.13) равна 8 % для КНР с па-

первом случае соответствующее время расчета составляло 1,4 с и

2,8 с – во втором.

125

5.2.3. Специализированный метод Монте-Карло

КНР и его приближения представляют собой непрерывные функции, что удобно не для всех задач: например, проблемы оце-

нивания погрешности измерения ПФ или погрешности электрон-

ной микроскопии (EBSD) связаны со статистическими аспектами.

В этих случаях для исследования более удобно оперировать с дан-

ными в виде дискретного набора ориентировок. Отметим, что ре-

альный поликристалл состоит из конечного числа зерен, хотя и очень большого. Таким образом, необходимы численные алгорит-

мы для статистического моделирования распределения ориентаций зерен поликристаллического образца. В [5, 7] разработан метод Монте-Карло вычисления НР на SO(3). Укажем алгоритм для ста-

тистического моделирования НР на SO(3).

В этом алгоритме используется другая параметризация враще-

ния g SO(3) :

g g φ,θ,ψ g1 φ g2 θ g3 ψ ,

где – π<φ,ψ π , 0 θ π ,

раметрическим подгруппам gi t .

Шаг 1. Задаются параметры НР N αij ,αi , т.е. положительно

определенная матрица ij и действительные числа αi , i, j 1, 2, 3 .

Шаг 2. Задается показатель свертки n.

Шаг 3. Вычисляются собственные значения λ1, λ2 , λ3 и собст-

127

Шаг 7. Вычисляется случайное вращение, являющееся прибли-

ηij – независимые реализации равномерно распределенной случай-

ной величины на интервале [0, 1]. Для получения одного вращения,

являющегося приближенной реализацией нормально распределен-

ной на SO(3) величины, требуется 3n случайных равномерно рас-

пределенных на [0,1] чисел.

В [5, 7] показано, что скорость сходимости получаемого дис-

кретного приближения НР имеет порядок 1n относительно пока-

зателя свертки. Скорость сходимости метода Монте-Карло модели-

рования случайных вращений имеет порядок O N 12 , где N –

объем выборки.

Данный специализированный метод Монте-Карло использовал-

ся при нахождении ПФ {001} от ФРО в виде КНР с теми же пара-

метрами, что и для двух методов приближенного вычисления, из-

ложенных ранее. ПФ моделировались методом гистограмм на ос-

128

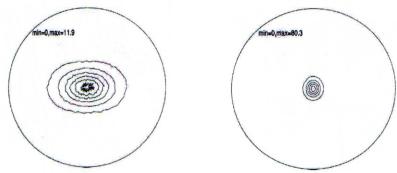
нове массива дискретных вращений, полученных методом Монте-

Карло. При вычислениях использовался параметр показателя свертки n = 20 и объем выборки N = 240 000 вращений. Точность вычислений оценивалась с помощью RP(0,01) путем сравнения по-

люсных фигур, вычисленных специализированным методом Мон-

те-Карло и полюсных фигур, вычисленных методом Фурье. Резуль-

тат погрешности вычислений равен 6 % для КНР с параметрами

на рис. 5.5 и 5.6. Соответствующее время расчета составляло 687 с

(см. рис. 5.5) и 801 с (см. рис. 5.6).

На рис. 5.5 и 5.6 мы видим эффект «дрожания» линий уровня,

который наблюдается в экспериментальных ПФ.

129

5.3. Выводы

В настоящей главе рассмотрены определение нормального рас-

пределения на группе вращений SO(3), удовлетворяющего цен-

тральной предельной теореме, и три способа приближенного его

вычисления.

1. Метод приближенного суммирования ряда Фурье удобен на

вает время вычисления.

2. Метод аналитического приближения базируется на вычисле-

нии простой функции, являющейся асимптотической формой КНР в точке максимума. Метод пригоден для вычисления КНР с доста-

точной точностью (2 – 3% в указанных примерах) для параметров

αii 0, 25 и требует для вычисления мало времени.

Метод суммирования ряда Фурье и метод аналитического при-

ближения, дающие непрерывную функцию как результат вычисле-

ния, используются для аппроксимации ФРО и ПФ.

3. Специализированный метод Монте-Карло основан на стати-

стическом моделировании вероятностей меры, аппроксимирует НР общего вида на группе вращений SO(3). Теоретически доказано,

что этот метод сходится к НР, которое может быть вычислено с заданной точностью (в рассмотренных примерах погрешность при-

130