
Лиситсын Молекулярная физика в задачакх 2014
.pdfОтметим еще один важный факт. Распределение Максвелла имеет место не только в газах, но в любой системе частиц, движе-
ние которых полностью подчиняется законам классической механики. В газах, как было отмечено, поступательное движение молекул полностью подчиняется законам классической механики (обычно говорят, что оно классично), поэтому распределение молекул по скоростям является максвелловским. Колебания атомов в кристаллической решетке твердых тел отнюдь не всегда являются классичными при комнатных температурах, при низких же температурах (Т ≤ 10 – 100 К) эти колебания совершенно перестают быть классичными. Соответственно, и распределение атомов решетки по скоростям также становится немаксвелловским. Движение электронов проводимости в металлах подчиняется законам квантовой механики вплоть до температур в несколько тысяч градусов, поэтому распределение электронов проводимости в металлах по скоростям всегда немаксвелловское.
Задача 5.1. В сосуде содержится газ, число молекул которого N. Сколько молекул из числа тех, что находятся в сосуде, имеют в точности заданную скорость, например 100 м/с?
Решение. Число таких молекул равно нулю. Действительно, как бы ни было велико число молекул в сосуде, но оно всегда конечно. Число же всевозможных значений скорости бесконечно велико. Но это и означает невозможность точного совпадения скорости какойлибо из молекул с любым точно заданным значением скорости.
Задача 5.2. Найдите вероятность того, что υx, υy, υz – проекции скорости молекулы на оси OX, OY, OZ находятся в пределах:
vвер < vx <vвер +0,01 vвер,
0 < vy <0,01 vвер, 0 < vz <0,01 vвер
Каким будет результат, если вместо проекции скорости vx рассмотреть модуль скорости, т.е. какова вероятность того, что модуль скорости молекулы будет иметь значение из интервала vвер< v < vвер + 0,01 vвер? С помощью понятия пространства скоростей дайте объяснение полученным результатам.
71

Решение. Согласно (5.1) и (5.2) доля от полного числа молекул, проекции скоростей которых vx, vy, vz попадают в заданные интервалы, записывается следующим образом:
dN(vx ,vy ,vz ) |
|
|
|
3 |
|
mv2 |
|
|
|||
|
|
m |
2 |
e− |
|
|
|||||
= |
|
dv dv |
dv |
. |
|||||||
2kT |
|||||||||||
|
|
|
|
||||||||
N |
|
2πkT |
|
|
|
|
|
||||
Строго говоря, ширина этих интервалов должна быть бесконечно малой, но с достаточно хорошей точностью эту формулу можно применять и для интервалов конечной ширины, лишь бы она была малой в сравнении с самой скоростью. Тем самым, ответ на первый вопрос задачи:
dN (v |
) |
|
|
|
m |
3 |
|
− mvx2 |
|
mv2y |
|
− mvz2 |
|
|
|
|||||||||
|
|
2 |
|
− |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x |
|
= |
|
|
|
|
|
|
e |
2kT e |
|
2kT e |
|
2kT dvxdvy dvz ≈ |
|||||||
|
|
N |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
− |
vвер |
|
0,01 vвер |
|
|
10−6 |
|
|
|
|
|||||||||||
|
vвер2 |
|
|
e |
−1 |
= 6,6 10 |
−8 |
|||||||||||||||||
≈ |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
vвер |
|
|
|
|
|
|
|
|
||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
π2 |
|
|
|
|
||||||
Ответ на второй вопрос получаем из (5.4) и (5.5) точно так же:
|
|
|
|
3/2 |
− mv |
2 |
|
4 v2 |
|
v2 |
|
||||||
dN(v) |
m |
|
|
|
− |
|
|
dv |
|
||||||||
|
2 |
|
vвер2 |
|
|||||||||||||
|
= 4π |
|
|
|
e |
2kT v |
dv = |
|
|
|
e |
|
|
|
|
≈ |
|
N |
|
|
|
2 |
|
|
|
vвер |
|||||||||
|
2πkT |
|
|
|
|
π vвер |
|
|
|
. |
|||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
≈ |
e−1 |
0,01 =8,3 10−3. |
|
|
|
|
|
||||||||
|
|
|
π |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Различие составляет, как видим, пять порядков! Почему же получились столь разные ответы, ведь величина скорости в обоих случаях была одной и той же – vвер, да и величина скоростного интервала тоже была одинаковой? Ответ
|
станет совершенно ясным, если обра- |
|
титься к иллюстрации нашего результа- |
|
та с помощью пространства скоростей |
|
(рис. 5.5).Если заданы проекции скоро- |
|
стей на координатные оси, то искомое |
|
число молекул совпадает с числом точек |
|
пространства скоростей, находящихся в |
|
маленьком кубике со стороной vx = |
Рис. 5.5 |
= vy = vz = 0,01vвер. Число же моле- |
|
72 |

кул, у которых задан модуль скорости, изобразится числом точек пространства скоростей, попадающих в промежуток между сферами с радиусами vвер и (vвер + 0,01vвер). Плотность точек в кубике и в сферическом слое одинакова, а объёмы этих фигур различаются более чем в 105 раз, во столько же раз различаются и количества соответствующих частиц.
Задача 5.3. Как изменится график функции распределения Максвелла, если увеличить температуру? Если увеличить массу молекул?
|
m |
3/2 |
|
− |
mv2 |
Решение. Максимум функцииF(v) = 4π |
|
e |
|
2kT v2 рас- |
|
|
|
||||
|
2πkT |
|
|
|
|
пределения Максвелла с ростом температуры, очевидно, сделается меньше, поскольку уменьшится множитель перед экспонентой
|
m 3/2 |
а |
|
значение экспоненты в точке максимума |
|||
|
|
|
, |
|
|||
|
|
||||||
|
2πkT |
|
|
|
|
|
|
|
|
|
|
2kT |
останется прежним, равным е |
–1 |
|
v = vвер |
= |
|
|
. Сама же точка |
|||
|
|||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
максимума сдвинется вправо по оси абсцисс. Тем самым, вид графика изменится, как изображено на рис. 5.6: из графика 1 получится график 2.
Увеличение массы приведёт |
F(v) m1 > m2 |
||
к обратному эффекту: макси- |
1 |
||
мум сдвинется влево и вырас- |
|||
тет (т.е. из графика 2 получится |
2 |
||
график 1). Однако все эти пре- |
T2 > T1 |
||
образования |
графика сохраня- |
|
|
ют площадь |
под |
графиком, |
v |
равную единице. |
|
||
|
Рис. 5.6 |
||
Отметим здесь, |
что распре- |
||
деление Максвелла фактически зависит не от температуры и массы отдельно, а от их отношения т/Т, поэтому изменение и массы и температуры в одно и то же число раз функцию распределения не меняет, например, графики функции распределения для молекулярного водорода (µ = 2 г/моль) при какой-либо температуре Т и гелия (µ = 4 г/моль) при температуре 2Т будут одинаковы.
73

Задача 5.4. С помощью функции распределения Максвелла дайте графическую интерпретацию утверждениям:
•вероятность молекуле иметь какую-либо скорость в заданном интервале;
•вероятность молекуле иметь скорость больше некоторой заданной;
•вероятность молекуле иметь в точности заданную скорость.
F(υ) |
Решение. Поскольку вероятность мо- |
||||
|
|
|
|
|
лекуле иметь скорость в заданном беско- |
|
|
|
|
|
нечно малом интервале (v, v + dv) равна |
|
|
|
|
|
|
|
|
|
|
|
F(v)dv, то вероятность попадания скоро- |
|
|
|
|
|
сти в конечный интервал (v1, v2) графи- |
|
|
|
|
|
|
|
|
|
|
υ |
чески изображается площадью заштрихо- |
|
|
|
|
ванной полоски (рис. 5.7). |
|
υ1 υ2 υ ' υ0 |
Вероятность молекуле иметь скорость |
||||
|
|
Рис. 5.7 |
|||
|
|
больше некоторой заданной v0 соот- |
|||
|
|
|
|
|
|
ветствует бесконечному значению v2, и поэтому изображается площадью заштрихованной области, где v > v0. Вероятность молекуле иметь в точности заданную скорость v' равна нулю, поскольку изобразится площадью соответствующего отрезка.
Задача 5.5. Найти число ударов молекул газа в единицу времени о стенку сосуда.
Решение. Решение задачи проведём в несколько этапов, постепенно уточняя результат.
Рассмотрим столкновения со стенкой пучка частиц, движущихся с одинаковой скоростью v в направлении, составляющем угол α с нормалью к стенке. За небольшой промежуток времени dt до стенки долетят и столкнутся с ней молекулы, которые в начальный момент находились от неё на расстоянии не более v dt. Все такие молекулы заполнят параллелепипед с площадью основания равной площади стенки S и высотой dh = v dt cosα (рис. 5.8). Число ударов dN за время dt будет равно числу молекул в этом параллелепипеде:
dN = n S dh = n S v cosαdt,
где n – число частиц в единице объёма пучка.
74

Число ударов ν в единицу времени |
n |
|
α |
|
получится делением dN на dt: |
|
|
||
ν = n S v cosα. |
(5.6) |
α |
vdt |
dh |
Совершенно ясно, что этот же ре- |
|
|||
|
|
|
||
зультат будет верен и тогда, когда раз- |
v |
|
|
|
ные молекулы падают на стенку с раз- |
S |
Рис. 5.8 |
|
|
ных сторон, но так, что направления их |
|
|
||
движения по-прежнему образуют угол α с нормалью к стенке. Пусть теперь скорости молекул по-прежнему одинаковы, но на-
правления их движения совершенно произвольны. При этом все направления движения молекул равновероятны. Для нахождения числа ударов молекул разобьём мысленно все молекулы на группы с близкими значениями углов между нормалью и направлениями движения молекул. Тогда число ударов молекул, которые летят в направлениях, образующих углы с нормалью в пределах от α до
α+dα запишется в соответствии с (5.6) следующим образом: |
|
dν = dn(α) S v cosα, |
(5.7) |
где dn(α) – число частиц в единице объёма, которые летят в направлениях, образующих углы с нормалью в пределах от α до α+dα. Поскольку все направления движения частиц равновероятны, то число частиц, летящих в пределах единичного телесного угла одинаково для всех направлений движения частиц. Тем самым:
dn(α) |
= |
n |
. |
(5.8) |
dΩ |
|
|||
|
4π |
|
||
Здесь dΩ – телесный угол, в пределах которого лежат направления движения интересующих нас частиц, 4π – полный телесный угол, т.е. угол, в пределах которого находится всё пространство.
Найдём телесный угол dΩ. Напомним, что телесным углом называется область пространства, ограниченная конической поверхностью. Величина телесного угла равна отношению площади сферического сегмента, вырезанного этой конической поверхностью на сфере произвольного радиуса R с центром в вершине данного конуса к квадрату радиуса этой сферы. В нашем случае величина телесного угла равна отношению площади закрашенного кольца к R2 (рис. 5.9). Площадь же этого кольца равна 2π R sinα R dα, а телесный угол, тем самым:
75
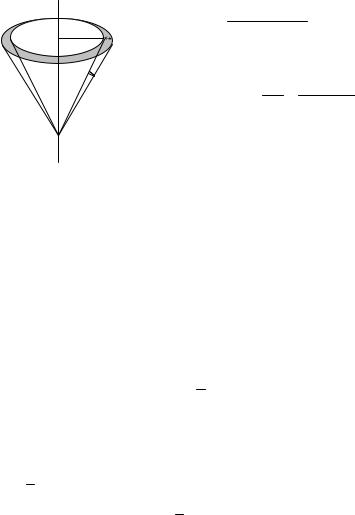
dΩ |
R sinα Rdα |
dα
R
α
dΩ = 2πR2 sin αdα = 2πsin αdα.
R2
Из (5.8) с учётом полученного результата найдём dn(α):
dn(α) = n dΩ = nsin αdα , 4π 2
а из (5.7) найдём dν:
dν = dn(α) S v cosα =
|
= |
1 |
|
Рис. 5.9 |
2 n S v cosα sin αdα. |
||
|
|
|
|
Проинтегрировав полученное равенство по всем α от нуля до π/2, получим искомое число ударов:
ν = |
1 nvS . |
(5.9) |
|
4 |
|
Учтём теперь, что скорости различных молекул неодинаковы. Полученный результат (5.9) можно применить к тем молекулам, скорости которых близки друг другу и лежат в интервале от некоторой величины v до v+dv. Но тогда n нужно заменить на dn(v): dn(v) = n F(v) dv.
Тем самым число столкновений таких молекул: dν = 14 nvF(v)dv .
Интегрируя это равенство по dυ от нуля до бесконечности, получим искомое число ударов:
ν = |
1 |
n |
|
S , |
(5.10) |
|
v |
||||||
4 |
||||||
|
|
|
|
|
где v – средняя скорость движения молекул:
∞
v = ∫vF(v)dv .
0
Задача 5.6. Найти давление идеального газа.
Решение. Для определения давления газа надо определить импульс, передаваемый стенке сталкивающимися с ней за единицу времени молекулами. Будем считать удары молекул абсолютно упругими, а стенку идеально гладкой (чуть позже увидим, что эти
76

требования не играют решающей роли для получения верного ответа). Тогда при столкновении меняется только перпендикулярная поверхности стенки составляющая скорости vz, причем это изменение сводится только к изменению ее знака. Следовательно, импульс, передаваемый при одном столкновении, равен
mvz – (– mvz) = 2mvz = 2mv cos α,
где т — масса молекулы, α – угол между направлением движения молекулы и нормалью к стенке (осью z). Поскольку согласно формуле (5.7) число молекул, движущихся со скоростью v и сталкивающихся со стенкой за единицу времени, равно
dν = dn(α) S v cosα = 12 n S v cosα sin αdα,
то импульс, переданный стенке этими молекулами, dpz = 2mvcosαdν = mn Sv2cos2α sin αdα.
Проинтегрируем полученное равенство по dα от нуля до π/2:
pz = mnSv2 |
π∫/2 cos2α sin αdα = |
1 |
mnSv2. |
|
3 |
||||
|
0 |
|
Учтём теперь, что скорости различных молекул неодинаковы. Полученный результат можно применить к тем молекулам, скорости которых близки друг другу и лежат в интервале от некоторой величины v до v+dv. Но тогда n нужно заменить на dn(v):
откуда |
|
|
|
|
dn(v) = n F(v) dυ, |
|
|
|
|
|
|||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
dpz = |
mSv2dn(v)= |
mnSv2 F (v)dv, |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∞∫v2 F (v)dv = |
|
|
|
|
|
|||||||||
|
1 |
|
|
1 |
|
|
|
2 mv2 |
|
||||||||
pz = |
mnS |
mnSv2 = |
nS = nkTS. |
||||||||||||||
3 |
3 |
3 |
|
2 |
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
Поскольку импульс, переданный стенке в единицу времени, есть сила, действующая на стенку, то давление оказывается таким:
р = nkT.
Записав n = N/V, получим уравнение состояния идеального газа в обычной форме:
рV = NkT.
77

В связи с полученным результатом вернёмся к исходным предположениям о характере столкновений молекул со стенкой. Уже сам по себе результат не содержит ничего, что указывало бы на необходимость идеализации. Суть же в том, что имеет место тепловое равновесие газа и стенки. А именно, поскольку газ как целое покоится, то импульс, переносимый молекулами, летящими к стенке, равен импульсу, уносимому молекулами, отражёнными от стенки. То же самое относится и к энергии, переносимой молекулами: поток энергии к стенке равен потоку энергии, уносимому молекулами, отражёнными от стенки. Ничего иного для получения нашего результата не требуется. Поэтому характер столкновения молекул со стенкой может быть любым. Наши исходные предположения лишь упростили вычисления.
Задача 5.7. Сосуд разделён на две части перегородкой с очень малым отверстием в ней. По разные стороны перегородки находится идеальный газ. Температуры газов по разные стороны перегородки Т1 и Т2. Найти отношение давлений по разные стороны перегородки. Газы разрежены.
Решение. Поскольку отверстие маленькое и газы разрежены, то равновесие в данном случае наступает, когда потоки молекул из одной части сосуда в другую одинаковы. Согласно решению предыдущей задачи это имеет место, если выполняется условие:
14 n1v1S = 14 n2v2S ,
где S –площадь отверстия, n1 и n2, и v1 и v2 – плотность числа
частиц, и, соответственно, средние скорости молекул по разные стороны перегородки. Тем самым:
|
|
|
|
n1 |
v1 = n2 |
|
2 . |
|
|||||||||
|
v |
||||||||||||||||
Поскольку, |
согласно уравнению |
состояния идеального газа |
|||||||||||||||
n = р/kT, то |
|
|
p1 |
|
|
|
|
|
|
p2 |
|
|
|
|
|
||
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|||||
|
|
|
|
v |
v |
||||||||||||
|
|
|
kT |
|
|
kT |
|
||||||||||
|
|
|
1 |
|
|
2 |
|||||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
||||||
Поскольку |
|
~ T , то получаем окончательно: |
|||||||||||||||
v |
|||||||||||||||||
|
|
|
|
|
p1 |
= |
|
p2 |
. |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
||||

Задача 5.8. В разреженном газе, масса молекул которого т, давление р, температура Т, движется диск радиуса r. Скорость и диска мала по сравнению с тепловой скоростью молекул. Диск движется вдоль своей оси. Оценить силу сопротивления газа, действующую на диск.
Решение. Будем считать поверхность диска гладкой, а удары молекул о диск упругими. Перейдём в систему отсчёта связанную с диском. В этой системе отсчёта газ как целое движется к диску со скоростью u. Тогда в этой системе отсчёта к скорости каждой молекулы добавится скорость движения диска u. Выберем систему координат с осью OX перпендикулярной диску, направив эту ось в сторону движения газа (рис. 5.10). Определим силу давления газа на ту из сторон диска, на которую натекает газ.
Для этого надо определить им- |
|
|
||||
пульс, |
передаваемый этой |
стороне |
u |
r |
||
за одну |
секунду сталкивающимися |
|||||
x |
||||||
|
||||||
с ней молекулами. Так как при –(vx+u) |
–vx+u |
|||||
столкновении меняется только пер- |
vx+u |
vx–u |
||||
пендикулярная |
поверхности диска |
|
|
|||
составляющая |
скорости, |
причем |
|
Рис. 5.10 |
||
это изменение сводится только к изменению ее знака, то импульс, передаваемый при одном столкновении, равен m(vx + u) – (– m(vx + + u)) = 2m(vx + u), где т — масса молекулы. За 1 с до диска долетят молекулы из объёма цилиндра с высотой (vx + u) и площадью основания равной площади диска πr2. Если молекул в единице объёма n, то с диском за 1 с столкнутся n(vx + u)πr2 молекул и передадут ему импульс 2nт(vx + u)2πr2.
Молекулы, приближающиеся к диску с противоположной стороны, передадут ему импульс 2nт(vx – u)2πr2, направленный в противоположную сторону. Таким образом, диск получит импульс, равный разности этих величин:
2nт(vx + u)2πr2 – 2nт(vx – u)2πr2 = 2nт2vx2u πr2 = 8nmπr2vxu.
При выводе этой формулы мы действовали так, как если бы у всех молекул проекция скорости vx одна и та же. На самом деле это совсем не так. В единице объёма скорость, близкую к υx, имеют dn(vx) = nϕ(vx)dvx молекул.
79

Такие молекулы передадут диску импульс
dpx = 8dn(vx)mπr2vxu = 8nϕ(vx)mπr2 vx u dvx.
Интегрируя по dvx от нуля до бесконечности, найдём p =8nmπr2u∞∫ϕ(vx )vxdvx =8nmπr2u vx .
0
Здесь vx = ∞∫ϕ(vx )vxdvx – среднее значение модуля проекции ско-
0
рости на ось OX в неподвижном газе. Поскольку импульс, переданный диску за 1 с, есть сила, действующая на диск, то полученная формула и даёт искомый результат. Вычислим vx :
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
m |
∞ |
mv2 |
|
|
|
|
|||
|
|
|
x = ∫ϕ(vx )vxdvx = |
|
|
∫e− |
x |
vxdvx = |
||||||||||||||
|
|
|
|
|
2kT |
|||||||||||||||||
|
v |
|
||||||||||||||||||||
|
|
|
|
2πkT |
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
m |
∞ |
|
− |
mv2x |
v2 |
|
|
|
m |
|
kT |
|
kT |
|
||||
= |
|
|
|
∫ |
e |
|
2kT d |
x |
|
= |
|
= |
. |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2πkT |
|
|
|
|
2 |
|
|
|
2πkT m |
|
|
2πm |
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
Кроме того, согласно уравнению состояния идеального газа n=р/kT, и тогда выражение для силы приобретает вид:
F =8 |
p |
mπr2u |
kT |
=8pπr2 |
m |
u. |
|
kT |
2πm |
2πkT |
|||||
|
|
|
|
Сила, как и следовало ожидать, пропорциональна давлению газа, площади диска и скорости его движения.
Уточним, где же мы использовали предположения о том, что диск движется медленно, а газ разреженный? Медленность движения диска мы использовали при подсчёте импульса, переданного молекулами, движущимися вслед за диском. Если бы диск двигался очень быстро, то эти молекулы просто не могли бы догнать диск и столкнуться с ним. Мы же считали, что все молекулы достигают диска. Разреженность газа также играла свою роль. Мы неявно предполагали, что после столкновения молекулы уходят от диска и больше с ним не сталкиваются. В плотном газе это не так: молекула, столкнувшаяся с диском, уйдёт от диска на весьма небольшое расстояние, где столкнётся с другими молекулами. В результате таких столкновений весьма заметна вероятность того, что эта молекула вновь столкнётся с диском.
80
