Лиситсын Молекулярная физика в задачакх 2014

Как видим, любая машина вне конкуренции с человеческим трудом.

Очевидно, что остальные 94 % химической энергии, выделяющейся в теле человека, превращаются просто в тепло и переходят в окружающую среду. Отметим, что у животных КПД того же порядка, что и у человека, поскольку температура тела у всех млекопитающих мало отличается от температуры человеческого тела.

Задача 6.8. Животным пустыни приходится преодолевать большие расстояния между источниками воды. Как зависит максимальное время, которое может бежать животное, от размеров животного L?

Решение. Запас воды пропорционален объему тела, т.е. L3, испарение же – площади поверхности, т.е. L2. Поэтому максимальное время пробега от одного источника до другого прямо пропорционально размерам тела животного: t ~ L.

Заметим, что максимальное расстояние, которое может пробежать животное, также растет пропорционально L (см. следующую задачу). Поэтому караван должен останавливаться на отдых тогда, когда устают собаки, сопровождающие караван.

Задача 6.9. Как зависит скорость бега животного по ровному месту и в гору от размеров животного L?

Решение. На рис. 6.5 показана картина В.А. Серова «Выезд императора Петра II и цесаревны Елизаветы Петровны на охоту»: собака бежит рядом со скачущей лошадью. Выясним, насколько прав был художник в своих наблюдениях.

Мощность, развиваемая животным, пропорциональна L2 (КПД мышц примерно постоянен – около 6 %, остальные 94 % химической анергии переходят в тепло; теплоотдача же пропорциональна площади поверхности тела, т. е. L2, значит, и полезная мощность пропорциональна L2).

91

Сила сопротивления воздуха прямо пропорциональна квадрату скорости и площади поперечного сечения (об этой зависимости более подробно речь пойдёт в п. Турбулентность):

F ~ υ2L2.

Поэтому затрачиваемая на ее преодоление мощность Fυ пропорциональна кубу скорости:

Fυ ~ υ2L2υ ~ υ3L2.

Итак, υ3L2 ~ L2, следовательно, υ ~ L0. И действительно, скорость бега по ровному месту у животных не мельче зайца и не крупнее лошади практически не зависит от размера особи.

Для бега в гору необходима мощность mgυ ~ L3υ; поскольку развиваемая мощность ~L2, находим υ ~ L–1. И действительно, собака легко взбегает на холм, а лошадь замедляет шаг.

Задача 6.10. Как зависит от размеров животного высота прыжка? Решение. Нужная для прыжка на высоту h энергия mgh пропорциональна L3h, а совершаемая силой мышц F работа пропорциональна FL. Сила F пропорциональна L2 (так как прочность костей

пропорциональна площади их сечения). Итак,

L3h ~ L2L,

т. е. высота прыжка h~L0 и не зависит от размеров животного. И действительно, тушканчик и кенгуру прыгают примерно на одинаковую высоту.

Природа необратимости. Все тепловые явления в конечном итоге сводятся к механическому движению атомов и молекул тела. Поэтому необратимость тепловых процессов на первый взгляд находится в противоречии с обратимостью всех механических движений. На самом деле это противоречие только кажущееся.

Пусть какое-нибудь тело скользит по другому телу. Благодаря трению это движение будет постепенно замедляться и, в конце концов, система придет в состояние теплового равновесия, причем движение прекратится. Кинетическая энергия двигавшегося тела перейдет в тепло, т.е. в кинетическую энергию беспорядочного движения молекул обоих тел. Очевидно, что этот переход энергии в тепло может осуществиться бесчисленным множеством способов: кинетическая энергия движения тела как целого может распреде-

92

литься между колоссальным числом молекул колоссальным числом способов. Другими словами, состояние равновесия, в котором макроскопическое движение отсутствует, может осуществиться неизмеримо большим числом способов, чем состояние, в котором значительная энергия сконцентрирована в виде кинетической энергии упорядоченного движения – движения тела как целого.

Следовательно, переход из неравновесного состояния в равновесное представляет собой переход из состояния, которое может осуществиться меньшим числом способов, в состояние, которое может осуществиться несравненно большим числом способов. Ясно, что наиболее вероятным будет то состояние тела (или системы тел), которое может осуществиться наибольшим числом способов,– это и будет состояние теплового равновесия.

Поэтому если предоставленная самой себе (т.е. замкнутая) система в некоторый момент времени не находится в состоянии равновесия, то в последующее время подавляюще вероятным будет переход ее в состояние, которое может осуществиться несравненно большим числом способов, т.е. приблизится к равновесию.

Наоборот, после того как замкнутая система пришла в состояние равновесия, подавляюще маловероятным был бы самопроизвольный выход системы из этого состояния.

Таким образом, необратимость тепловых процессов имеет вероятностный характер. Самопроизвольный переход тела из равновесного состояния в неравновесное, строго говоря, не невозможен, а лишь подавляюще менее вероятен, чем переход из неравновесного состояния в равновесное. В конечном итоге необратимость тепловых процессов обусловливается колоссальностью числа частиц – молекул, из которых состоят тела.

Можно получить представление о том, сколь маловероятно самопроизвольное отклонение тела из состояния равновесия, хотя бы на примере расширения газа в пустоту.

Пусть газ находится первоначально в одной из половин сосуда, разделенного перегородкой на две равные части. При открытии отверстия в перегородке газ распространится равномерно по обеим частям сосуда. Обратный же переход газа в одну из половин сосуда без постороннего вмешательства никогда не произойдет. Причину

93

этого легко выяснить простым подсчетом. Каждая молекула газа при своем движении в среднем проводит одинаковое время в обеих частях сосуда. Можно сказать, что вероятность ее нахождения в каждой из половин сосуда равна 1/2. Если газ можно считать идеальным, то его молекулы движутся независимо друг от друга. Поэтому вероятность найти две данные молекулы одновременно в одной половине сосуда составляет (1/2)2 = 2–2. Вероятность же найти все N молекул газа в одной части сосуда равна 2–N. Так, для сравнительно небольшого количества газа, содержащего, скажем, 1020 молекул, эта вероятность изобразится чудовищно малым числом:

2−1020 ~ 10−31019 .

Другими словами, такое явление можно было бы наблюдать примерно один раз в течение времени, изображающегося числом

– безразлично секунд или лет, так как и секунда, и год

(1 год ~ 3 107 с), и даже продолжительность существования Земли (~ 4 млрд. лет) одинаково малы по сравнению с этим промежутком времени.

Такого же рода чудовищно малым числом изображается, как показывает расчет, вероятность самопроизвольного перехода всего 1 Дж теплоты от тела с температурой 0 °С к другому телу, температура которого на 1 оС больше.

Из этих примеров ясно видно, что возможность заметного самопроизвольного обращения теплового процесса имеет, по существу, чисто абстрактный характер; его вероятность столь мала, что необратимость тепловых процессов фактически можно считать принципиальной.

Однако вероятностная природа необратимости проявляется в том, что в природе все же происходят самопроизвольные отклонения от равновесия, хотя и весьма ничтожные и кратковременные. Такие отклонения носят название флуктуаций. Благодаря флуктуациям, например, плотность и температура в различных небольших участках находящегося в равновесии тела не остаются точно постоянными, а испытывают некоторые, хотя и весьма ничтожные колебания (далее мы оценим масштаб флуктуаций аддитивных физиче-

94

частиц в системе). Так, температура 1 мг воды, находящегося в равновесии при комнатной температуре, будет испытывать колебания порядка 10–8 градуса. Существуют, однако, и такие явления, в которых флуктуации играют существенную роль.

Задача 6.11. В закрытом сосуде объемом V в отсутствие силовых полей находятся N молекул идеального газа. Определить среднее число молекул и его флуктуации в объеме υ, являющемся малой частью объема V.

Решение. Разделим сосуд на части, объёмом υ каждая. Всего таких частей будет z =V/υ.

Пусть пi – число молекул в i-й части. Очевидно

N = n1 + n2 + n3 +… + nz.

Поскольку все части одинаковы, то и средние числа молекул n в них также одинаковы:

Определим теперь флуктуацию п. В качестве величины, характеризующей флуктуацию, возьмём корень квадратный из среднего значения квадрата разности п и n :

n = (n −n )2 ,

(n −n )2 = n2 −2nn + n 2 = n2 −n 2.

Введём величину fi (её называют индикатором), определив её

i≠ j

95

= N f 2 +∑ fi f j = N f 2 + N(N −1) f 2 .

i≠ j

Здесь мы положили fi f j = fi f j , поскольку молекулы движутся

независимо одна от другой и наличие одной молекулы в данном месте никак не зависит от присутствия какой-либо другой молекулы. Далее:

Из определения величины fi понятно, что fi = fi2, но тем самым f = f 2 = Vυ .

Поэтому

n2 = (n −n )2 = n2 −n 2 = N f 2 + N(N −1) f 2 −(N f )2 = = N ( f 2 − f 2 )= Nf (1− f ) ≈ Nf = n.

числа молекул воздуха составляет 10–6? Давление 105 Па, температура 290 К.

Решение. Согласно результату предыдущей задачи nn = n1 ,

откуда находим n1 =10−6 , n = 1012 .

По уравнению состояния идеального газа рV = NkT. Число молекул в единичном объёме

откуда

V = 1012/2,5·1019 = 0,4 10–7 см3.

Если этот объём имеет форму кубика с ребром а, то

а3 = V = 0,4 10–7 см3,

откуда а ~ 3,5 10–3 см.

Заметим, что размер 3,5 10–3 см = 35 мкм примерно соответствует толщине человеческого волоса.

Энтропия. Количественной характеристикой теплового состояния тела, описывающей его стремление переходить в другие состояния, является число микроскопических способов, которым это состояние может быть осуществлено. Это число называют статистическим весом состояния; обозначим его буквой Г. Тело, предоставленное самому себе, стремится перейти в состояние с большим статистическим весом. Принято, однако, пользоваться не самим числом Г, а его логарифмом, который еще умножают на постоянную Больцмана k. Определенную таким образом величину S = klnГ называют энтропией тела.

Число способов Г, которыми может осуществиться состояние системы, состоящей, например, из двух тел, равно произведению чисел способов Г1 и Г2, которыми могут быть осуществлены состояния каждого из этих тел в отдельности: Г = Г1 Г2. Поэтому

S = klnГ = klnГ1 + klnГ2 = S1 + S2.

Мы видим, что энтропия сложной системы равна сумме энтропий ее частей (именно для достижения этого свойства и служит логарифм в определении энтропии).

Закон, определяющий направление тепловых процессов, можно сформулировать как закон возрастания энтропии: при всех проис-

ходящих в замкнутой системе тепловых процессах энтропия системы возрастает.

Максимальное возможное значение энтропии замкнутой системы достигается в тепловом равновесии. Это утверждение является более точной количественной формулировкой второго закона тер-

97

модинамики. Данный закон был открыт Клаузиусом, а его молеку- лярно-кинетическое истолкование было дано Больцманом.

Обратно, можно сказать, что всякий процесс, при котором энтропия замкнутой системы тел возрастает, является необратимым; причем чем больше возрастание энтропии, тем больше степень необратимости. Идеальному случаю полностью обратимого процесса в замкнутой системе соответствует случай, когда энтропия этой системы оставалась бы неизменной.

Точное определение того, что именно подразумевается под «числом микроскопических способов осуществления» теплового состояния тела, дается в квантовой статистической физике. Только после этого появляется возможность фактического вычисления энтропии различных тел и установления ее связи с другими тепловыми величинами.

Более глубокий теоретический анализ позволяет установить соотношение, являющееся основой для термодинамических применений понятия энтропии. Это соотношение связывает приращение dS энтропии тела при бесконечно малом обратимом изменении его состояния с количеством получаемого им в этом процессе теплоты dQ (речь идет при этом, конечно, о незамкнутом теле, так что обратимость процесса не требует постоянства его энтропии!). Оно

имеет вид

dS = dQT ,

где Т – температура тела.

Самый факт существования связи между dS и dQ вполне естествен. Сообщение телу теплоты приводит к усилению теплового движения его атомов, т. е. к увеличению хаотичности их распределения по различным состояниям микроскопического движения, а тем самым к увеличению статистического веса. Естественно также, что влияние заданного количества теплоты на изменение теплового состояния тела характеризуется относительной величиной этого количества по сравнению с полной внутренней энергией тела и потому убывает с увеличением его температуры.

Если процесс получения телом теплоты необратим, то есть параллельно с этим процессом идут процессы приближения тела к состоянию теплового равновесия (при которых энтропия всегда

98

возрастает), то связь между приращением энтропии и полученной телом теплотой превращается в неравенство:

dSнеобр > dQT .

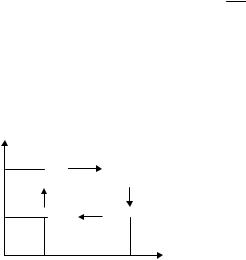
Задача 6.13. Изобразите график цикла Карно в переменных T, S. Укажите на графике количество теплоты, полученной от нагревателя, количество теплоты, отданной холодильнику, и работу за

каждой из изотерм одинаковы по величине и отличаются друг от друга знаком; при изотермическом расширении энтропия растёт, при изотермическом сжатии убывает:

S2 = – S1 = S2 – S1.

Тепло, полученное от нагревателя Q2 = T2 (S2 – S1) равно площади четырёхугольника S1ABS2, тепло, отданное холодильнику, Q1 = T1 (S2 – S1) равно площади четырёхугольника S1DCS2.

Работа за цикл равна

A = Q2 – Q1 = (T2 – T1) (S2 – S1),

т.е. площади прямоугольника ABCD. Отсюда находим КПД цикла:

Интегрируя, получим

S =CV lnT + RlnV +const =CV ln p +Cp lnV +const.

Из последнего выражения для энтропии найдём

S =CV ln P +Cp lnV +const =ln pCV +lnV Cp +const,

S =ln(pCV V Cp )+const, pCV V Cp =econst S , pV γ =econst S .

Константы во всех полученных выражениях остаются неопределёнными. Эта неопределённость есть следствие термодинамического определения энтропии.

Задача 6.15. На графике (рис. 6.7) в переменных р, V изображены адиабатические процессы, совершаемые некоторой массой идеального газа. Изобразите эти же процессы в переменных T, S.

Решение. На каждой из адиабат энтропия остаётся постоянной. Согласно результату предыдущей задачи адиабата располагается тем выше, т.е. выше давление р при заданном объёме, чем выше

100