Лиситсын Молекулярная физика в задачакх 2014

Из полученного результата находим, в частности, скорость на поверхности потока:

v(h) = ρ2ghη2 sin α.

Как видим, скорость на поверхности потока пропорциональна квадрату его глубины. Объём жидкости dQ, протекающей в единицу времени через поперечное сечение слоя единичной ширины и толщиной dy (этот слой изображён на рисунке пунктиром), равен dQ = v(y)dy,

и согласно найденной формуле для скорости запишется в виде

Интегрируя по всей глубине потока, найдём:

Q = ρ3ghη3

Заметим, что глубина потока h растёт как корень кубический из расхода жидкости:

h ~ 3 Q.

Причём рост этот очень резкий при малых расходах (рис. 9.4, б), т.е. для обеспечения даже сравнительно небольшого расхода требуется поток конечной глубины. Этим можно объяснить известный факт, состоящий в том, что вода со стенок мокрого стакана или чашки полностью не стекает. По мере стекания воды толщина плёнки воды, оставшейся на стенке, будет уменьшаться, что ещё более снизит скорость воды. Тем самым вода скорее испарится со стенки стакана, нежели стечёт с него. Именно это мы и наблюдаем в действительности.

Задача 9.3. Жидкость течет по цилиндрической трубке с радиусом а и длиной L под влиянием перепада давлений р = р2 – р1 на концах этой трубки. Считая, что скорость и течения жидкости направлена везде вдоль оси трубки, а по величине меняется в перпен-

131

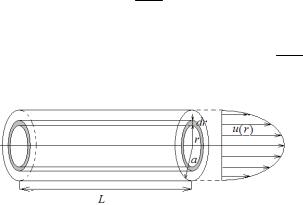
дикулярном оси (радиальном) направлении в зависимости лишь от одной координаты – расстояния r от оси, найдите зависимость скорости от расстояния до оси трубки, а также расход жидкости.

Решение. Поток импульса, переносимого в радиальном направ-

лении:

Π = −ηdudr .

Рассмотрим объем жидкости, ограниченный проведенной внутри трубки коаксиальной с ней цилиндрической поверхностью некоторого радиуса r. Полный поток импульса через эту поверхность (её площадь есть 2πrL) равен

2πrLΠ = −2πηrL dudr .

Это и есть сила трения, действующая на рассматриваемый объем жидкости со стороны остальной жидкости. Она уравновешивается силой перепада давлений (приложенных к основаниям цилин-

Константа определяется из условия равенства нулю скорости на поверхности самой трубки, т. е. при r = а. Окончательно получаем u = 4ηpL (а2 −r2 ).

Таким образом, скорость меняется по квадратичному закону от нуля на стенке до максимального значения uмакс = 4ηpL а2 на оси трубки (рис. 9.5).

Рис. 9.5

132

О полученном нами результате говорят, что текущая в трубке жидкость имеет параболический профиль скоростей.

Определим количество (массу М) жидкости, вытекающей в единицу времени из трубки. Обозначим через dV(r) объем жидкости, вытекающей в единицу времени через кольцо внутренним радиусом r и шириной dr:

dV(r) = u(r)dS = u(r)2πrdr,

где и(r) – скорость жидкости на расстоянии r от оси, а dS = 2πrdr – площадь кольца радиуса r и ширины dr. Поскольку u(r) нам известна, то

dV (r) = u(r)2πrdr = 4ηpL (а2 −r2 )2πrdr = 2πΔηLp (а2 −r2 )rdr.

Отсюда

(произвольная постоянная положена равной нулю, поскольку должно быть V(0) = 0). Полный объем жидкости, вытекающей из трубки за единицу времени, есть значение V(r) при r = а:

V (a) = πΔ8ηpaL4 .

Умножив его на плотность жидкости ρ, найдем искомую массу

М = πρΔ8ηpaL 4 = πΔ8vLpa4 .

Эта формула называется формулой Пуазейля. Мы видим, что количество вытекающей из трубки жидкости пропорционально четвертой степени радиуса трубки.

Задача 9.4. Как зависит от температуры вязкость газа? Решение. Выше было показано, что кинематическая вязкость га-

за по порядку величины совпадает с его коэффициентом диффузии ν ~ λv (λ – длина свободного пробега молекул, v – тепловая скорость молекул газа). Плотность газа ρ = n m, где т – масса одной молекулы, a n – число молекул в единице объема; поэтому для коэффициента вязкости η = ρν получаем выражение

133

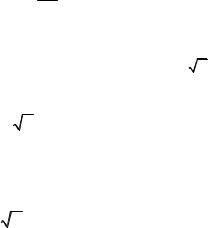
η~ nmvλ ~ mσv ,

где σ – сечение столкновений. Мы видим, что коэффициент вязкости, как и коэффициент теплопроводности, не зависит от давления газа. Поскольку тепловая скорость v пропорциональна Т , можно считать, что и коэффициент вязкости газа пропорционален корню из температуры:

η ~ Т .

Это заключение, однако, справедливо лишь в той степени, в которой можно считать постоянным сечение столкновений σ. Выше указывалось, что сечение несколько возрастает при уменьшении температуры. Соответственно этому вязкость убывает с уменьше-

нием температуры быстрее, чем Т .

Вязкость жидкостей обычно убывает с повышением температуры; это естественно, поскольку при этом облегчается взаимное перемещение молекул. У маловязких жидкостей, например у воды, это падение хотя и заметно, но не очень значительно.

Число Рейнольдса. Мы рассмотрели простейшие задачи о движении жидкости. В более сложных случаях точное решение задачи наталкивается обычно на очень большие математические трудности и, как правило, оказывается невозможным. Например, не может быть решена в общем виде задача о движении в жидкости тела даже такой простой формы, как шар.

В связи с этим, при исследовании различных вопросов о движении жидкости приобретают большое значение простые методы, основанные на соображениях о размерности тех физических величин, от которых это движение может зависеть.

Рассмотрим, например, равномерное движение твердого шара через жидкость, и пусть задача заключается в определении испытываемой шаром силы сопротивления F. Вместо того, чтобы говорить о движении тела через жидкость, можно было бы говорить и о вполне эквивалентной задаче об обтекании неподвижного тела потоком жидкости; такая постановка задачи отвечает наблюдениям над обтеканием тел потоком газа в аэродинамической трубе.

134

Физические свойства жидкости, определяющие ее течение или движение в ней посторонних тел, характеризуются всего двумя величинами: ее плотностью ρ и коэффициентом вязкости η. Кроме того, в рассматриваемом случае движение зависит еще от скорости шара u и от его радиуса а. Таким образом, в нашем распоряжении есть всего четыре параметра со следующими размерностями:

Из них можно составить безразмерную величину. Прежде всего, исключить размерность массы можно лишь одним способом – разделив η на ρ:

[ν]= [η/ρ] = см2/с.

Далее, для исключения размерности времени делим и на ν: [u/ν] = 1/см.

Безразмерную величину мы получим, умножив отношение u/ν на радиус а. Эту величину обозначают символом Re:

Re = uνа = ρηuа

и называют числом Рейнольдса. Она является очень важной характеристикой движения жидкости. Очевидно, что всякая другая безразмерная величина может быть только функцией этого числа.

Вернемся к определению силы сопротивления. Она имеет размерность г см/с2. Величиной с такой размерностью, составленной из тех же параметров, является, например, ρи2а2.

Всякая другая величина той же размерности может быть представлена в виде произведения ρи2а2 на некоторую функцию безразмерного числа Рейнольдса. Поэтому можно утверждать, что искомая сила сопротивления выражается формулой вида:

F = ρu2a2 f (Re).

Разумеется, неизвестная функция f (Re) не может быть определена из соображений размерности. Однако с помощью этих соображений нам удалось свести задачу об определении функции четырех параметров – силы F в зависимости от ρ, u, η и а – к задаче об

135

определении всего одной функции f (Re). Эта функция может быть определена, например, экспериментально. Измерив силу сопротивления, испытываемую каким-либо одним шариком в какой-либо одной жидкости, и построив по полученным данным график функции f (Re), мы тем самым получим возможность узнать силу сопротивления для движения любого шара в любой жидкости.

Для стационарного движения в жидкости тел любой другой формы под величиной а в числе Рейнольдса надо понимать какойлибо линейный размер тела заданной формы, и мы получаем возможность сравнивать течения жидкости вокруг геометрически подобных тел, отличающихся лишь своими размерами. Движения, отличающиеся значениями параметров ρ, u, η, а при одинаковом значении числа Рейнольдса, называют подобными. Вся картина движения жидкости в таких случаях отличается лишь масштабами всех своих характеристик: расстояний, скоростей и т. д.

Все сказанное относится не только к жидкости, но и к газам, при том условии, что плотность среды (жидкости или газа) в процессе движения не испытывает сколько-нибудь заметного изменения, так что ее можно считать постоянной (несжимаемая среда). Хотя с обычной точки зрения газ является легко сжимаемой средой, но те изменения давления, которые возникают в газе при его движении, обычно недостаточны для сколько-нибудь существенного изменения его плотности. Газ перестает вести себя как несжимаемая среда лишь при скоростях, сравнимых со скоростью звука.

Задача 9.4. Из несжимаемой жидкости, заполняющей всё пространство, внезапно удаляется сферический объём радиуса а. Оцените время, за которое образовавшаяся полость заполнится жидкостью. Вязкостью жидкости пренебречь, давление в жидкости р, плотность жидкости ρ.

Решение. Оценим время на основании анализа размерностей параметров, определяющих искомую величину. Размерность давления:

[р]= сила/площадь = масса/длина время2.

Избавимся от размерности массы, поделив давление р на плотность ρ:

136

Поделив р/ρ на квадрат размера полости а, избавимся от размерности длины:

Тем самым, получаем величину, имеющую размерность времени:

Полученная формула и даёт искомую оценку времени заполнения полости жидкостью. Точное решение задачи приводит к ответу:

Для полости в воде размером а ~ 1 см и давлении порядка 1 атм время оказывается порядка 10–3 с. Оцените сами скорость жидкости, заполняющей полость, и давление в жидкости в момент захлопывании полости.

Задача 9.5. При землетрясениях в океане возникают протяжённые колебания уровня поверхности океана – волны цунами. Оцените скорость с распространения таких волн, приняв глубину океана равной h.

Решение. Аналогично предыдущей задаче произведём оценку скорости волн на основании анализа размерностей величин, определяющих процесс распространения волн. Очевидно, что колебания воды вызваны силой тяжести, поэтому скорость волн должна зависеть от ускорения свободного падения g, размерность которого [g] = м/с2. Для получения нужной нам размерности м/с можно составить единственную комбинацию:

c ~ gh.

Интересно, что точное решение задачи приводит к точно такому же ответу:

c = gh.

137

Средняя глубина океана составляет около 4 км, тем самым скорость цунами в океане составляет порядка 200 м/с (720 км/ч). У берега глубина воды значительно меньше, соответственно уменьшается и скорость волн, но растёт их высота, поскольку передние участки волны замедляются при подходе к берегу, в то время как задние участки движутся по более глубокой воде и нагоняют передние части волны.

Задача 9.5. Наблюдаемые нами волны на воде обычно возникают под действием ветра. В отличие от цунами такие волны вызывают колебания воды лишь вблизи её поверхности, распространяясь вглубь воды на расстояния порядка длины волны. Оценить скорость с распространения таких волн, приняв длину волны равной λ.

Решение. Аналогично предыдущей задаче скорость волн должна зависеть от ускорения свободного падения g, размерность которого [g] = м/с2. Для получения нужной нам размерности м/с можно составить единственную комбинацию:

c ~ gλ.

Скорость таких волн имеет величину порядка скорости ветра, поэтому длина волн

λ ~ c2 . g

Высота волн обычно не превосходит λ/10. Для штормовых ветров, скорость которых c ~ 20–25 м/с, длина волн оказывается около 40–60 м, а их высота 4–6 м.

Формула Стокса. При достаточно малых скоростях движения сила сопротивления всегда пропорциональна первой степени скорости. Поскольку сила сопротивления подчиняется формуле F =ρи2а2 f(Re), то при малых скоростях функция

f (Re) = constRe .

Тогда получим

F = ρи2 а2 f (Re) = ρи2 а2 ηconstρuа = const ηau.

138

Как видим, если сила сопротивления пропорциональна скорости движения, то она автоматически пропорциональна также и линейным размерам тела (и коэффициенту вязкости жидкости). Определение коэффициента пропорциональности в этом законе требует более детальных вычислений.

Для движения шара в жидкости оказывается, что const = 6π, т.е.

F = 6πηau.

где а – радиус шара (эта формула называется формулой Стокса). Уточним теперь, что именно подразумевается под «достаточной

малостью» скорости движения, обеспечивающей применимость формулы Стокса. Поскольку речь идет о виде функции f (Rе), то искомое условие должно относиться к значениям числа Рейнольдса, а поскольку число Re и скорость и (при заданных размерах тела) пропорциональны друг другу, то ясно, что условие малости скорости должно быть выражено в виде условия малости числа Re:

Отсюда видно, что условие «достаточной малости» скорости имеет относительный характер. Фактическая величина допустимых скоростей зависит от размеров движущегося тела (и от вязкости жидкости). При очень малых размерах (например, для взвешенных в жидкости мельчайших частиц, совершающих броуновское движение) формулу Стокса можно применять и для скоростей, которые с других точек зрения уже нельзя было бы считать малыми.

Задача 9.5. Шарик радиуса а падает в широкий сосуд, наполненный вязкой жидкостью. Найдите скорость и установившегося (равномерного) движения шарика. Коэффициент вязкости жидкости равен η, плотность жидкости ρж, плотность шарика ρ.

Рассмотрите случай падения стального шарика в сосуд с глицерином. Вязкость глицерина η = 15 г/с см2, его плотность ρгл = 1,25 г/см3, плотность стали ρ = 7,8 г/см3. Решить аналогичную задачу для падения в воздухе стального шарика и дождевых капель.

Решение. На шарик, падающий в вязкой среде действуют три силы: сила тяжести P = mg, архимедова сила FА= ρжVg и сила сопротивления

139

Fсопр = 6πηаи,

где V – объем шарика, а ρ и ρж – соответственно плотность материала шарика и среды, и – скорость шарика. Написав массу m

Скорость и шарика в процессе его падения монотонно возрастает, но ускорение шарика dи/dt уменьшается с ростом скорости и обращается в ноль при некоторой скорости, которую мы назовем установившейся скоростью и обозначим её через и0. Приравняв ускорение dи/dt равным нулю, получим значение установившейся скорости

и0 = (ρ−ρж )Vg . 6πηа

Найдем теперь закон движения шарика. Поделим обе части уравнения (9.3) на 6πηа и обозначим τ = m/6πηа. Тогда уравнение приобретёт вид

τ ddtи = и0 −и.

Очевидно, что τ имеет размерность времени. Поделив обе части полученного уравнения на τ(и – и0) и проинтегрировав по dt, получим

ln(и0 −и) = −τt +const

или после потенцирования

− t

и = и0 − Ae τ , (9.4)

где А – постоянная величина, значение которой найдем из начального условия, состоящего в том, что при t = 0 скорость шарика и = 0. Тогда из (9.4) следует, что А = и0. Окончательно находим:

− t

и= и0 1−e τ .

140