Баев Теория колебаниы 2015

математической модели системы столь важен поиск новых независимых интегралов движения.

Пусть функция f(t,q,p) является интегралом уравнений Гамильтона. Тогда она должна обращаться в константу на фазовых траекториях системы f(t,q,p) = const, и, следовательно, для решений

которому с помощью скобок Пуассона можно придать более компактный вид:

, ! " , !# " , !# $ , , !% $, !, %,

и теорема доказана.

Теорема Якоби – Пуассона дает автоматически правило, позволяющее из двух известных интегралов с помощью скобок Пуассона получить третий интеграл. Однако при этом следует иметь ввиду, что новый интеграл может оказаться либо тождественно равным нулю, либо функцией от предыдущих известных интегралов. Поэтому всегда требуется специальная проверка на независимость нового интеграла движения, найденного с помощью скобок Пуассона.

52

Выражение (1.159) и доказательство теоремы Якоби – Пуассона являются двумя примерами из обширных приложений скобок Пуассона в механике. В качестве еще одного примера приведем

1.13. Канонические преобразования

Преобразования координат в 2n-мерном фазовом пространстве,

называются каноническими, если они сохраняют канонический вид уравнений Гамильтона:

Важность канонических преобразований состоит в том, что они позволяют связать данную гамильтонову систему координат с другой гамильтоновой системой координат, в которой математическая модель может быть более простой, чем в исходной.

Непосредственно из определения канонических преобразований следуют их важные свойства. Если в фазовом пространстве выполнить два канонических преобразования, то результирующее

53

преобразование снова будет каноническим. В частности, тождественное преобразование есть каноническое преобразование, как и преобразование, обратное каноническому. Такое множество математических объектов образует группу со всеми присущими ей свойствами [7].

Справедливо следующее утверждение [3]: преобразования координат (1.163) фазового пространства являются каноническими тогда и только тогда, когда существует такая функция F, при которой тождественно выполняется равенство

Постоянная с в равенстве (1.167) всегда отлична от нуля, так как выражение в правой части этого равенства не является полным

можно считать, что производящая функция имеет вид функции S от

этих переменных:

1.170

Для свободных канонических преобразований выражение (1.167)

принимает вид

)m δ ( .δ 0 m δ & δ 2 δ6$ , , (%. 1.171

можно перебрать все свободные канонические преобразования.

При этом, однако, задаваясь производящей функцией, всякий раз следует проверять выполнение условия (1.169), которое, применительно к свободным каноническим преобразованиям,

Гамильтона свободное каноническое преобразование должно явно зависеть от времени.

1.14. Инварианты

На языке математики инвариантность – неизменность величины по отношению к некоторой группе преобразований системы координат, в которой эта величина представлена.

В данном параграфе будут рассмотрены основные инварианты аналитической механики.

Инвариант Пуанкаре – Картана. Выведем выражение для

а также учитывая выражение для гамильтониана (1.126), получим следующее выражение для вариации действия:

положения системы являются прямыми, то интеграл в правой части выражения (1.179) обращается в нуль, и оно принимает вид

соединим точки этих контуров прямыми путями. В результате получится цилиндрическая поверхность, которая изображена на рис. 1.7 и которую назовем трубкой прямых путей.

57

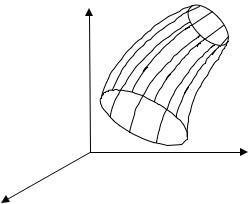
Вычислим действие W вдоль образующих трубки от кривой С0 до

( )

t

(C1)

(C0)

p

q

Рис. 1.7. Трубка прямых путей

Интегрируя последнее выражение по α в пределах от α=0 до α=1, получаем следующее выражение, составленное из криволинейных интегралов, взятых вдоль замкнутых контуров (С0) и (С1),

взятый вдоль замкнутого контура (С), не меняет своего значения при произвольном смещении (с деформацией) этого контура вдоль трубки прямых путей.

Поскольку деформацию контура в фазовом пространстве можно рассматривать как результат его канонических преобразований, то, в конечном итоге, приходим к следующему утверждению: криволинейный интеграл (1.186), взятый вдоль замкнутого контура (С), размещенного на трубке прямых путей, для систем, движение которых описывается каноническими уравнениями Гамильтона, является инвариантом по отношению к каноническим преобразованиям фазового пространства.

Этот интеграл называют инвариантом Пуанкаре – Картана. Можно доказать обратное утверждение [3]: пусть интеграл Пуанкаре – Картана (1.186) является интегральным инвариантом по отношению к

59

где 7 1, … , 8.

Иначе говоря, для любой трубки прямых путей интеграл Пуанкаре – Картана, вычисленный вдоль охватывающего трубку замкнутого контура, не изменяет своей величины при произвольном смещении контура вдоль образующих трубки. Тогда уравнения (1.187), (1.188) – это уравнения Гамильтона.

Последнее означает, что инвариантность интеграла Пуанкаре – Картана имеет для аналитической механики фундаментальное значение, поскольку может быть положена в ее основу, а именно: постулируя эту инвариантность, получаем из нее канонические уравнения Гамильтона.

Еще раз хочется обратить внимание на то, о чем уже говорилось выше: время входит в инвариант Пуанкаре – Картана наравне с обобщенными координатами, так что его можно рассматривать как обобщенную координату, а функцию Гамильтона как соответствующий ей обобщенный импульс. При этом в качестве аргумента канонических уравнений Гамильтона можно выбрать любую обобщенную координату, тогда ее обобщенный импульс будет играть роль функции Гамильтона.

Положим, что в качестве независимой переменной выбрана первая обобщеннаяm координата, , m . Обозначим символом К ее обобщенный импульсo , , m . К( , а функцию Гамильтона обозначим символом z=

Тогда интеграл Пуанкаре – Картана будет выглядеть так: