Баев Теория колебаниы 2015

Если при инжекции в ускоритель удается заполнить зарядами всю область устойчивости, ограниченную сепаратрисой, то сгусток заряженных частиц в дальнейшем не пульсирует. Если же в ускоритель инжектируется монохроматический пучок с разбросом импульсов существенно меньшим вертикального размаха сепаратрисы (3.2.22), то сгусток при ускорении пульсирует по длине, поскольку область, занятая пучком, вращается внутри сепаратрисы, причем отмеченная выше нелинейная зависимость частоты фазовых колебаний от амплитуды вызывает искажение фазового объема пучка, как показано на рис. 3.2.4.

Рис.3.2.4. Фазовые портреты сгустка, захваченного в режим ускорения, в разные моменты времени

Численное интегрирование уравнений фазовых колебаний, учитывающее явную зависимость гамильтониана от времени в

241

процессе ускорения заряда, дает его фазовый портрет, изображенный на рис. 3.2.5.

Область устойчивости на рис. 3.2.5 заштрихована, причем она оказывается незамкнутой, а точка устойчивого равновесия становится фокусом. Таким образом можно говорить, что эффект ускорения эквивалентен силе трения, вызывающей затухание фазовых колебаний, и при этом система, т.е. заряд, движущийся в поле бегущей волны, перестает быть гамильтоновой.

Тем не менее сопоставление сепаратрисы, изображенной на рис. 3.2.5 с сепаратрисой, построенной выше в адиабатическом приближении, показывает, что во многих практически интересных случаях их различие не велико.

D

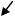
° ψ

Рис. 3.2.5. Фазовый портрет заряда с учетом эффекта его ускорения

В частности, хвост сепаратрисы численного моделирования вносит небольшой вклад в общую площадь области устойчивости. Это совпадение результатов, найденных разными методами, очень важно, поскольку преимущество адиабатического приближения состоит в том, что с его помощью параметры системы удается увязать между собой в аналитической форме через условия устойчивости и, таким образом, получить наглядную и потому очень удобную информацию о влиянии этих параметров на характер движения системы. Более того, можно достаточно корректно, с помощью аналитических методов, учесть влияние на фазовые колебания эффекта ускорения. В случае

242

малых фазовых колебаний подобная математическая модель имеет вид [13]

3.2.26

В уравнении (3.2.26) коэффициенты при ψ и ψ являются функциями времени, причем в рассматриваемых здесь в качестве примера ионных ускорителях эти функции меняются достаточно медленно, чтобы ускоряемый ион можно было считать

в параграфе 2.2.8 и применим его к рассматриваемой системе. Согласно выражению (2.2.156),

В заключение остановимся на слове «резонансный» в названии ускорителей. Появление его связано с тем, что ускоряемый заряд как система работает в режиме резонанса, когда собственная частота колебаний системы (ускоряемого заряда) совпадает с частотой внешнего на нее воздействия, частотой ускоряющего поля.

Действительно, с точностью до адиабатического приближения

ускоряющей волны или что то же самое, ω ωП , где ωП это частота колебаний ускоряющей гармоники. А последнее равенство есть не что иное, как условие резонанса, когда система (ускоряемый заряд) теряет устойчивость, увеличивая свою энергию за счет энергии внешнего силового (электромагнитного) поля.

Таким образом, заряд, ускоряющийся в поле бегущей волны, неустойчивая система, работающая в режиме резонанса, что и объясняет появление слова «резонансный» в названии ускорителя. Более подробно о конструкциях, принципе работы и теории устройств, в которых реализуется резонансный принцип ускорения, можно прочесть в книге [5].

3.3.Бетатронные колебания

Вэтом параграфе, в качестве примера, рассмотрим так называемые бетатронные колебания, совершаемые заряженными частицами в циклическом ускорителе. Принципиальная схема такого ускорителя представлена на рис.3.3.1.

R

УС

+

Рис.3.3.1. Принципиальная схема циклического ускорителя.

Основными его элементами являются ускоряющая система (УС), проходя через Oкоторую частица получает порцию энергии, и магнитное поле , направленное на рисунке перпендикулярно его плоскости. Идея работы ускорителя состоит в том, что магнитное поле, возвращая заряженную частицу к ускоряющей системе,

244

заставляет эту частицу за время цикла ускорения пройти ее много раз и приобрести в конечном итоге требуемую энергию.

Введем очень важное в дальнейшем понятие равновесной орбиты. Равновесной будем называть такую орбиту, по которой должны двигаться заряженные частицы при номинальных условиях.

Вданном примере физической системой является заряженная частица, движущаяся в магнитном поле. Для описания этого движения удобно использовать цилиндрическую систему координат (z,r,θ), ось z которой направлено вдоль магнитного поля.

Вчастности, на рис. 3.3.1 представлен случай с азимутальносимметричным магнитным полем, которое не зависит от азимута θ и в

котором равновесная орбита, являясь окружностью, лежит в плоскости его симметрии, называемой медианной плоскостью. Тем не менее этот рисунок отражает идею всех циклических ускорителей.

Даже если в момент старта заряженная частица находилась на равновесной орбите и имела номинальные начальные условия, при которых она должна была бы двигаться по равновесной орбите, то довольно быстро эта частица соскочит с нее по трем причинам. Вопервых, из-за кулоновского расталкивания частиц в ускоряемом пучке, во-вторых, из-за рассеяния на молекулах остаточного газа. Естественно, что в рабочей области, где ускоряются заряженные частицы, должен поддерживаться высокий вакуум, иначе частице будут терять приобретаемую энергию в соударениях с молекулами газа. Однако путь, проходимый частицами за время ускорения, на порядки превосходит длину свободного пробега в вакууме, и столкновения с молекулами газа неизбежны. Наконец, третья причина состоит в том, что практически все частицы имеют начальную поперечную скорость, из-за которой они сойдут с равновесной орбиты, даже если находились на ней в момент старта.

Поэтому необходимы силы, которые бы удерживали заряженные частицы на равновесной орбите, т.е. необходима их фокусировка. При ее наличии частицы будут совершать колебания около равновесной орбиты, которые получили названия бетатронных, поскольку, по началу, их теория была построена применительно к бетатрону, ускорителю электронов, или, как их одно время называли, β-частиц, в силу чего ускоритель и колебания зарядов в нем получил такое название.

245

Таким образом, бетатронные колебания – это колебания заряженных частиц в магнитном поле около равновесной орбиты.

Бетатронные колебания считаются устойчивыми, если их амплитуда не возрастает, в противном случае они считаются неустойчивыми.

Как уже отмечалось выше, бетатронные колебания будем рассматривать в цилиндрической системе координат, ось z которой направлена вдоль силовых линий магнитного поля. При этом вертикальную составляющую бетатронных колебаний, вдоль оси z, будем называть вертикальными бетатронными колебаниями, а их радиальную составляющую – радиальными бетатронными колебаниями. Подобное разделение в терминологии бетатронных колебаний по их составляющим оказалось не только удобным для их описании, но и вполне обоснованным, поскольку эти колебания оказываются главными или нормальными колебаниями системы, которые в линейном приближении не зависят друг от друга.

здесь индексом «0» отмечены радиус равновесной орбитыи величина магнитного поля на равновесной орбите.

Величина n называется показателем спада магнитного поля и

окрестности равновесной орбиты продиктован тем обстоятельством, что она позволила получить условие устойчивости бетатронных колебаний в очень простой и потому удобной форме.

Можно показать [5], что в азимутально-симметричном магнитном поле бетатронные колебания являются устойчивыми, если выполнено

т. е. магнитное поле спадает по радиусу, но не сильно.

246

Магнит циклического ускорителя, в котором пространственная структура магнитного поля удовлетворяет условию (3.3.2), называется слабофокусирующим.

Однако одного условия устойчивости недостаточно Для определения размеров вакуумной камеры, в которой движется пучок, необходимо знать амплитуды бетатронных колебаний, зависящих от начальных условий зарядов пучка и пространственной структуры магнитного поля. А эти зависимости можно найти только из уравнений бетатронных колебаний, т.е. из их математической модели.

Построим линейную математическую модель бетатронных колебаний, для чего найдем линейную аппроксимацию магнитного поля вблизи равновесной орбиты.

Начнем с линейной аппроксимации его вертикальной компоненты. Разложим в ряд Тейлора вертикальную составляющую магнитного поля, ограничившись в этом разложении линейным

вертикальная составляющая в начале координат имеет максимум по переменной z, и поэтому O

В итоге, в линейном приближении выражение для вертикальной составляющей магнитного поля имеет вид

247

Найдем выражение в линейном приближении для радиальной компоненты магнитного поля, для чего сначала разложим ее в ряд

В силу азимутальной симметрии магнитного поля его радиальная компонента в начале координат равна нулю и имеет минимум, поэтому первые два слагаемых в разложении (3.3.7)) равны нулю.

соответственно, которые связаны между собой известными выражениями [2]

3.3.11

248

и расписав это векторное уравнение по координатам, получим

в азимутально-симметричном магнитном

249

здесь ω – так называемая циклотронная частота обращения заряда в магнитном поле

получим, в линейном приближении, уравнение радиальных

являются вертикальной и радиальной частотой бетатронных колебаний соответственно3.3.20 , 3.3.23

Уравнения известны как уравнения Керста – Сербера, названные так в честь инженеров, которые вывели их, анализируя динамику движения заряженных частиц в бетатроне [5].

Они представляют линейную модель бетатронных колебаний в азимутально-симметричном магнитном поле. Из этих уравнений

250