
Барменков Дополнителные главы курса ТФКП.Римановы поверкхности 2015
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
А.Н. Барменков, Е.В. Сандракова, Е.В. Сумин, В.Б. Шерстюков
Дополнительные главы курса ТФКП.
Римановы поверхности
Учебное пособие
Москва 2015
УДК 517.53(075.8) ББК 22.161.5я7 Д 68
Дополнительные главы курса ТФКП. Римановы поверхно-
сти: учебное пособие / А.Н. Барменков, Е.В. Сандракова, Е.В. Сумин, В.Б. Шерстюков. М.: НИЯУ МИФИ, 2015. – 36 с.
Настоящее учебное пособие представляет собой дополнительные главы курса ТФКП и посвящено римановым поверхностям.
Предназначено для студентов всех факультетов НИЯУ МИФИ, изучающих теорию функций комплексного переменного.
Рецензент канд. физ.-мат. наук, доц. НИЯУ МИФИ А.П. Карташев
ISBN 978-5-7262-2160-1
©Национальный исследовательский ядерный университет «МИФИ», 2015
ВВЕДЕНИЕ
Одним из высших достижений в математике XIX в. явилось создание в работах Абеля, Якоби, Римана, Вейерштрасса и других исследователей теории римановых поверхностей, алгебраических функций и тэта-функций. Идеи и методы теории римановых поверхностей с самого начала нашли глубокие приложения. Как было показано в работах Вейерштрасса, Ковалевской, Вебера, Кёттера, римановы поверхности могут применяться к решению сложных дифференциальных уравнений, возникающих в ряде задач аналитической механики и гидродинамики.
1. ПОСТРОЕНИЕ РИМАНОВОЙ ПОВЕРХНОСТИ ЭЛЕМЕНТАРНЫМ МЕТОДОМ
В основном курсе ТФКП довольно подробно рассмотрены свойства однозначных аналитических (голоморфных) функций. На самом деле при решении практических задач часто используют отображения, обратные к функциям, принимающим одно значение в нескольких или даже в счетном числе точек. Это означает, что функции, обратные к таким, являются многозначными.
Для того чтобы к многозначным функциям можно было применять понятия и результаты, полученные для однозначных функций, используют некоторую процедуру, называемую выделением однозначных ветвей этих функций.
Для устранения этой неоднозначности также применяются так называемыеримановы поверхности и римановы многообразия с использованием аппарата отображений. Поскольку обычно на этот материал не хватает времени в семестровом курсе ТФКП, то решено подробнее осветить эти вопросы в данном пособии.
Начнем с элементарного метода, в основе которого лежит выделение однозначных ветвей многозначной аналитической функции и последующее построение ее римановой поверхности.
3
Пусть z = F(w) – функция, определенная, однозначная и непре-
рывная (в обобщенном смысле) в области G расширенной ком-
плексной плоскости. Предположим, что область G удалось какимлибо способом разбить на конечное или счетное множество областей G1, G2, …, попарно не имеющих общих точек, так, что любая точка области G – внутренняя для одной только области Gk или же общая граничная, по крайней мере, для двух областей Gj и Gk, причем в каждой из этих областей отображение z = F(w) является вза-
имно однозначным. Тогда образ каждой из областей Gk будет также областью F(Gk ) = Dk и весь образ F(G) будет покрываться облас-
тями Dk, а также образами общих частей границ областей Gk. Рассмотрим функцию w = f (z) , обратную к z = F(w) , в каждой
из областей Dk, определяя ее тем дополнительным условием, что ее значения принадлежат Gk – прообразу области Dk. Тогда функция f (z) , вообще многозначная, представится посредством несколь-
ких, быть может бесконечно многих, однозначных и непрерывных (в обобщенном смысле) функций fk (z) . Каждую из них будем называть однозначной ветвью функции f (z) в соответствующей области Dk. При этом определении важно помнить, что характер областей Dk, а вместе с тем и однозначных ветвей функции fk (z) ,
существенно зависит от того, как именно область G разбита на области Gk. В простейших случаях область G допускает такое разбиение на области Gk, при котором соответствующие области Dk совпадают между собой. Пусть, например, Dk1 , Dk2 , ... совпадают с од-
ной и той же областью D′. Тогда многозначная функция w = f (z) обладает многими, быть может бесконечно многими, однозначными ветвями в области D′, а именно fk1 (z), fk2 (z), ... .
К сказанному нужно добавить, что для произвольной непрерывной функции z = F(w) разбиение области G на области Gk, удовле-
творяющие указанным ранее условиям, вообще говоря, невозможно. Однако для случая, когда F(w) – аналитическая в области G (за
исключением изолированных точек, в которых она может обращаться в ∞), подобное разбиение всегда возможно и при том бесконечно многими способами. Используем следующий факт: если
4
аналитическая функция z = F(w) многолистна в области G, то эту
область можно разбить на конечное или счетное число областей, в каждой из которых F(w) будет однолистной. Соответствующие
области Gk называются областями однолистности функции F(w). Напомним: F(w) однолистна в области G, если w1, w2 G,
w1 ≠ w2 : F(w1 ) ≠ F(w2 ) ; F(w) многолистна в области G, еслиw1, w2 G , w1 ≠ w2 : F(w1) = F(w2 ) . Проиллюстрируем указанный выше способ разбиения области G на области однолистности на некоторых элементарных функциях.
2. РИМАНОВА ПОВЕРХНОСТЬ ФУНКЦИИ w = n z
Функцию, обратную к функции z = wn , обозначим через w = n z. Так как
w = n |
|
z |
|
|
|
Arg z |
+i sin |
Arg z |
, |
|
||
|
|
cos |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||
то n значений w , w , ..., w |
|
в плоскости |
w |
, в которых z = wn |
при- |
|||||||
0 1 |
|
|
n−1 |
|
|
|
|
|
|
|
||
нимает одно и то же значение z, располагаются в вершинах правильного n-угольника, вписанного в окружность радиусом w = n z с
центром w = 0 . Обратно: вершины любого правильного n-угольника с центром в начале координат можно рассматривать как n значений
функции w = n z. Поэтому область G плоскости w будет областью
однолистности для z = wn тогда и только тогда, когда из n вершин любого правильного многоугольника с центром w = 0 она содержит не более, чем одну вершину. Очевидно, этому условию удовлетворя-
ет угол раствора 2nπ свершиной в начале координат.
Из начала координат w = 0 проведем n прямолинейных лучей под равными углами. Тогда получим, что вся плоскость w , в ко-
торой определена многолистная функция z = wn , разделится на n углов – областей однолистности этой функции:
|
|
|
2πk |
|
2π(k +1) |
|
k =0,1, 2, ..., n −1. |
|
Gk |
= w |
w : |
|
<ϕ< |
|
|
, |
|
n |
|
|||||||
|
|
|
|
n |
|
|
||
5
Образом каждой из этих областей Gk будет одна и та же область D′ плоскости z.
Попытаемся теперь построить такой геометрический образ, что-
бы степенная функция z = wn устанавливала взаимно однозначное и взаимно непрерывное соответствие между точками всей плоскости w и точками этого образа.
Рассмотрим первый угол 0 <ϕ< |
|
2π |
. Он отображается на всю |
||
|
|
||||
|
|
|
|
n |
|
плоскость |
z |
с выброшенной положительной полуосью (разре- |
|||
зом), т.е. |
D = |
z \ [0, +∞) . В соответствии с правилом обхода счи- |
|||
таем, что |
луч |
ϕ =0 переходит в |
верхний берег разреза, а луч |
||
ϕ = 2nπ – в нижний. Изготовим n экземпляров Dk ( k =0,1, ..., n −1 )
плоскости z с разрезом вдоль положительной действительной полуоси (область D′), являющихся образами углов G0 , G1 , ..., Gn−1 ,
подложим их друг под друга и склеим так, чтобы сохранить непрерывность и взаимную однозначность соответствия. Для этого ниж-
ний берег разреза 1-го листа D0 склеиваем с верхним берегом 2-го листа D1 (находящегося над ним), нижний берег разреза 2-го листа D1 склеиваем с верхним берегом разреза 3-го листа D2 и т.д., на-
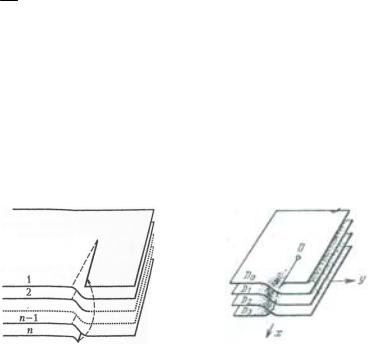
конец, нижний берег разреза n-го листа склеиваем с верхним берегом разреза 1-го листа (рис. 2.1, 2.2; на рис. 2.2 n = 4).
Рис. 2.1 |
Рис. 2.2 |
6

Построенный геометрический образ называется поверхностью
Римана функции |
w = n z . |
Полученные n функций |
wk |
(z) =(n z ) |
, |
||||||||
k =0,1, 2, ..., n −1, |
|
|
|
|
|
|
|
|
|
|
|
k |
|
для |
каждой из |
которых степенная функция |
|||||||||||
z = wn является обратной, |
|
образуют |
однозначные |
ветви много- |
|||||||||
значной функции |
w = n z . |
Выбор однозначных ветвей функции, |
|||||||||||
обратной |
к z = wn , |
определяется |
условием, что |
значения |
|||||||||
wk =(n z ) |
принадлежат области Gk . Так как z = wn |
имеет отлич- |
|||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
ную от нуля производную во всех точках области Gk , |
то по свой- |
||||||||||||
ству производной обратной функции |
|
|
|
|
|
|
|||||||
|
|
(n z )′ = |
|
1 |
= |
|
1 |
, |
|
|
|
||
|
|
|
n−1 |
|
n−1 |
|
|
|
|||||
|
|
|
k |
|
|
nw |
n(n z )k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так что для каждой ветви многозначной функции имеет место известная формула
(n z )′ = |
1 |
|
. |
n(n z ) |
n−1 |
||
|
|
|
Поэтому и для многозначных функций сохраняются все свойства аналитических функций. Подчеркнем, что и при другом разбиении
области w на области однолистности для функции z = wn обрат-
ная многозначная функция все равно сохраняет все свойства аналогичной функции при рассмотренном выше разбиении.
Отметим, что точка, при обходе которой в достаточно малой ее окрестности совершается переход от одной ветви многозначной функции к другой ее ветви, называется точкой ветвления (разветвления) этой многозначной функции. Причем если после n-кратного обхода в одном и том же направлении опять возвращаемся на начальную ветвь, то говорят, что это точка ветвления n-го порядка, в противном случае – бесконечного порядка. Точки ветвления конечного порядка называются алгебраическими точками ветвления. Точки z = 0 и z =∞ являются алгебраическими точками ветвления
n-го порядка функции w = n z . В этих точках сама функция принимает по одному значению: n 0 = 0 , n ∞ = ∞ . На поверхности Рима-
7

на они будут концевыми точками разрезов, общими для всех лис-
тов Dk ( k =0,1, 2, ..., n −1).
Замечание 2.1. Аналогично строится риманова поверхность для бесконечнозначной функции w = Ln z , которая является обратной к
z =ew . Отличие от римановой поверхности для |
w = n z состоит в |
том, что бесконечное счетное число полос |
|
Gn ={w w : 2πn < Im w < 2πn + 2π} , n = 0, ±1, ± 2 , …, |
|
преобразуется функцией z =ew в область D = |
z \ [0, +∞) . Значит, |
риманова поверхность состоит из бесконечного счетного числа
листов. |
Отметим, что точки ветвления z = 0 и z = ∞ функции |
w = Ln z |
называются логарифмическими точками ветвления и яв- |
ляются точками ветвления бесконечного порядка. |
|
3. РИМАНОВА ПОВЕРХНОСТЬ ФУНКЦИИ w = Arcsin z
Эта функция определяется как обратная к z =sin w . Поскольку
sin w = |
eiw −e−iw |
, то все основные ее свойства задаются отображе- |
|
|
2i |
||
|
|
|
|
ниями eiw |
и e−iw . |
||
В односеместровом курсе ТФКП подробно рассматриваются свойства экспоненты: эта функция не является однолистной во всей комплексной плоскости. В частности, областями однолистности
функции eiw являются полосы |
|
|
|
Rn ={w |
: 2πn −π< Re w < 2πn +π} , |
n = 0, ±1, ±2, ..., |
|
которые преобразуются в одну область D = |
z \ (−∞, 0] . Аналогич- |
||
но, можно показать, что функция |
z =sin w |
взаимно однозначно и |
|
конформно отображает полосу |
|
|
|
Gn = w |
w : πn − π < Re w < πn + π , |
n = 0, ±1, ±2, ..., |
|
|
2 |
2 |
|
на область D = |
z \ ((−∞, −1] [1, +∞)) и непрерывно продолжается |
||
на замкнутую полосу Gn . Причем для каждой области Gn граничный луч
8
|
|
π |
|
||
Re w = |
|
|
|
+πn, Im w ≥ 0 |
|
2 |
|||||
|
|
||||
(соответственно, луч |
|
|
|
|
|
|
π |
|
|||
Re w = |
|
|
|
+πn, Im w ≤ 0 ) |
|
2 |
|
||||
|
|
|
|||
биективно (взаимно однозначно) отображается на верхний (соответственно, нижний) берег разреза [1, +∞) , а луч
|
|
|
π |
+ πn, Im w ≥ |
|
|
Re w = − |
2 |
0 |
||
|
|
|
|
|
|
(соответственно, луч |
|
|
|
|
|
|
|
π |
|
|
|
Re w = − |
2 |
+ πn, Im w ≤0 ) – |
|||
|
|
|
|
|
|
на верхний (соответственно, нижний) берег разреза (−∞, −1].
Это позволяет следующим образом построить риманову по-
верхность функции w = Arcsin z , |
которая содержит бесконечное |
|||
счетное число листов. |
|
|
||
Возьмем |
бесконечный |
набор |
||
{Dn : n } |
экземпляров |
области |
||
D = |
z \ ((−∞, −1] [1, +∞)) |
(об- |
||
ласть Dn рассматривается при этом |
||||
как образ области Gn при отобра- |
||||
жении |
z =sin w ). Склеим далее для |
|||
каждого k |
экземпляры |
D2 k |
и |
|
D2 k +1 , как обычно говорят, «крест- |
||||
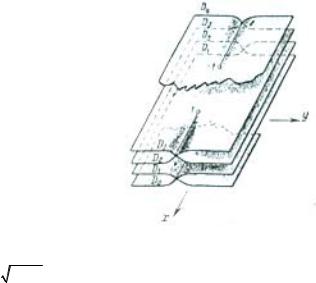
накрест» (рис. 3.1, здесь |
k = 0,1). |
|||
Отметим, что в точке z = ∞ функция |
||||
w = Arcsin z |
имеет две логарифми- |
|||
ческие точки ветвления (одну обра- |
||||
зуют четные экземпляры области D, |
||||
другую – нечетные). К этому же вы- |
|
|
воду можно прийти, исследуя вы- |
Рис. 3.1 |
|
ражение арксинуса через логарифм |
||
|
||
Arcsin z = −i Ln ( 1− z2 +iz). |
|
9
4. РИМАНОВА ПОВЕРХНОСТЬ ФУНКЦИИ w = z + z2 −1 ,
ОБРАТНОЙ К ФУНКЦИИ ЖУКОВСКОГО z = |
1 |
|
1 |
|
|
w + |
|
|
|
2 |
|
|||
|
|
w |
||
В качестве экземпляров листа, из которого будет построена требуемая риманова поверхность, возьмем плоскости с выброшенным отрезком [−1, 1] . Это и будут области Dk , k = 0,1. Как известно,
функция, обратная к функции Жуковского, имеет две ветви. Обозначим их, соответственно, через f0 (z) и f1 (z) . Эти ветви, соответственно, отображают области D0 и D1 на внутренность и внешность единичного круга. Так как f0 (z) отображает на верхнюю по-
луокружность нижний берег отрезка [−1, 1] , а f1 (z) – верхний, |
то |
нужно склеить между собой нижний берег разреза на листе D0 |
и |
верхний берег разреза на листе D1 . То же самое нужно сделать с верхним берегом разреза на D0 и нижним на D1 , которые отображаются на нижнюю полуокружность. Полученная двулистная по-
верхность и есть риманова поверхность функции w = z + z2 −1 . Эта функция имеет точки ветвления второго порядка над точками
z = ±1 . Данную поверхность можно |
получить |
из поверхности |
||||||||||||||
w = z |
дополнительными дробно-линейными |
отображениями. |
||||||||||||||
Действительно, представим функцию Жуковского |
z = |
1 |
w + |
1 |
|
в |
||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
w |
|
|||
|
|
z −1 |
w −1 |
2 |
|
|
|
z = |
ξ+1 |
|
||||||
виде |
|
|
|
|
= |
. Дробно-линейные отображения |
|
|
|
и |
||||||
z +1 |
ξ−1 |
|||||||||||||||
|
|
w +1 |
|
|
|
|
|
|
||||||||
ω= |
w +1 |
|
переводят функцию w = z + |
z2 −1 в функцию ω= |
ξ . |
|
||||||||||
w −1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10
