
Барменков Дополнителные главы курса ТФКП.Римановы поверкхности 2015
.pdfими представлениями римановой поверхности. Возникающие при этом функции перехода w = w(z) и обратно z = z(w) голоморфны.
Из проведенных рассуждений следует, что неособые римановы поверхности являются комплексными многообразиями (комплексной размерности 1).
Выбор в качестве локального параметра z или w не всегда является самым удобным. Есть и другие способы выбора локального параметра τ так, что
z = z(τ); |
τ Ω, |
||||
σ: |
|
|
|
||
w = w(τ), |
|
||||
где z(τ) и w(τ) – голоморфные функции от τ, причем |
|||||
dz |
, |
dw |
≠θ. |
||
|
|
|
|
||
|
|
||||
d τ |
|
d τ |
|
||
Риманова поверхность σ, заданная в 2 уравнением
F(z, w) = wn +a (z)wn−1 |
+... +a (z) =0 |
|
|
1 |
n |
(где a1(z), ..., an (z) |
– многочлены), |
расположена на z-плоскости |
n-листно. Точный |
смысл этого |
утверждения таков: пусть |
π: σ → – проекция римановой поверхности σ на z-плоскость, задаваемая формулой
(z, w) σ: π(z, w) = z.
Тогда для почти всех z полный прообраз π−1 (z) состоит из n различных точек поверхности σ:
(z, w1 (z)), ..., (z, wn (z)) ,
где w1 (z), ..., wn (z) – n корней уравнения
F(z, w) = wn +a1 (z)wn−1 +... +an (z) =0
при данном z. При некоторых значениях z некоторые из точек образа могут сливаться; образуются точки ветвления.
21

Точки ветвления на поверхности σ могут быть найдены из усло-
вия обращения в нуль производной ∂∂Fw .
Точка ветвления удовлетворяет системе уравнений
F (z, w) = 0;
,= 0.
Вокрестности тех точек римановой поверхности, где ∂∂Fw ≠ 0 ,w)(z∂w∂F
проекция π: σ → локально изоморфна.
Проекции точек ветвления римановой поверхности σ на z- плоскость ищутся, поэтому, как нули дискриминанта R(z) много-
члена F(z, w) :
R(z) = ∏(wi (z) − wj (z)) –
i≠ j
наибольший общий делитель многочленов F(z, w) и ∂F(z, w) .
∂w
В неособом случае на поверхности σ имеется, таким образом, лишь конечное число точек ветвления.
Пример 6.1. Пусть σ: w2 = Pn (z) , где Pn (z) – многочлен степе-
ни n.
Поверхность σ является гиперэллиптической. Она двулистно расположена над z-плоскостью. Здесь
F(z, w) = w2 − Pn (z),
grag F ={−Pn′(z), 2w} .
Точка (z0 , w0 ) является особой, если
ω0 =0 , Pn′(z0 ) = 0 ,
т.е. (z0 , w0 ) удовлетворяет системе уравнений
22
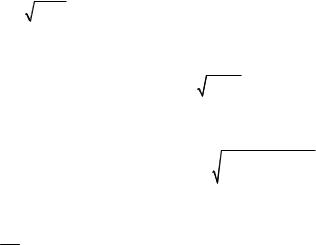
Pn (z0 ) = 0;Pn′(z0 ) = 0,
где z0 – кратный корень многочлена Pn (z) .
Итак, |
условие неособенности |
римановой поверхности σ: |
w2 = P (z) |
есть условие отсутствия кратных корней у многочлена |
|
n |
|
|
Pn (z) : |
|
|
|
n |
|
|
Pn (z) =∏(z − zi ), zi |
≠ z j при i ≠ j. |
i=1
Найдем точки ветвления этой неособой римановой поверхности. Для их определения решаем систему уравнений
ω2 = Pn (z);
w = 0.
Получаем n точек ветвления Pi (zi , 0) σ, i =1, 2, ..., n .
В окрестности любой точки поверхности σ, отличной от точки ветвления, в качестве локального параметра естественно взять z, и
w = Pn (z) – голоморфная функция.
В окрестности точки ветвления Pj в качестве локального параметра удобно взять
τ= z − z j .
Тогда для точек римановой поверхности σ получим локальное параметрическое представление
z = z j + τ2 , w = τ ∏(τ2 − zi − z j ) ,
j≠i
где радикал есть однозначная голоморфная функция для достаточно малых τ (подкоренное выражение не обращается в нуль), причем dwdτ ≠ 0 при τ = 0 , i =1, 2, ..., n ; j =1, 2, ..., n .
23
Пусть τ – локальный параметр в окрестности точки ветвления P0 (z0 , w0 ) поверхности σ. Будем считать, что z(0) = z0 , w(0) = w0 . Тогда
|
|
+ aτ |
s |
+O(τ |
s+1 |
); |
|
z = z0 |
|
τ→0, |
|||||
|
|
|
|
|
|||
|
|
+bτq +O(τq+1 ), |
|||||
w = w |
|
||||||
|
0 |
|
|
|
|
|
|
где a и b – отличные от нуля коэффициенты. Поскольку в окрестности точки ветвления P0 в качестве локального параметра можно взять w, то q =1 . Получаем вид поверхности σ в окрестности точки ветвления:
|
|
+ aτ |
s |
+O(τ |
s+1 |
); |
|
z = z0 |
|
τ→0, |
|||||
|
|
|
|
|
|||
σ: |
|
+bτ+O(τ2 ), |
|
||||
w = w |
|
|
|||||
|
0 |
|
|
|
|
|
|
причем s >1 .
7. РИМАНОВЫ ПОВЕРХНОСТИ КАК ДВУМЕРНЫЕ ВЕЩЕСТВЕННЫЕ МНОГООБРАЗИЯ. КОМПАКТИФИКАЦИЯ РИМАНОВОЙ ПОВЕРХНОСТИ. РОД РИМАНОВОЙ ПОВЕРХНОСТИ
В разд. 6 было отмечено, что произвольная риманова поверхность с вещественной точки зрения является двумерной поверхностью (двумерным многообразием). Что можно сказать о топологии этой поверхности?
Задача 7.1. Доказать, что эта поверхность связна. Утверждение 7.1. Риманова поверхность σ ориентирована.
Доказательство. Пусть z = x +iy , w =u +iv . Если z = x +iy –
локальный параметр в некоторой области U на σ, то x, y – вещественные координаты в U.
Второй |
локальный параметр |
w =u +iv |
связан |
с первым |
||
z = x +iy |
голоморфной функцией |
w = w (z) , |
dw |
≠ 0 , |
определяю- |
|
dz |
||||||
|
|
|
|
|
||
щей гладкую замену вещественных координат
24

u =u(x, y);v = v(x, y).
Якобиан этой замены |
|
|
|
|
|
|
|
|
|
|
∂u |
∂u |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
det J (u(x, y),v(x, y)) = |
∂x |
∂y |
= |
|
dw |
|
> 0 |
на U. |
|
|
|
||||||||
|
∂v |
∂v |
|
|
dz |
|
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|
Что и означает ориентируемость.
Пока сделанные наблюдения о связности и ориентированности римановых поверхностей не дают возможность классифицировать их по топологическому типу. Не хватает компактности.
Рассмотрим процедуру компактификации римановой поверхности σ, т.е. добавления к ней нескольких точек, превращающих ее в компактное комплексное многообразие, а значит, в замкнутую ориентированную поверхность.
1. Комплексная z-плоскость компактифицируется добавлением к одной бесконечно удаленной точки ∞. В качестве локаль-
ного параметра в окрестности ∞ нужновзять ζ = 1z . В общей части
действия локальных параметров z и ζ, где z ≠ 0 и ζ ≠ 0 , возникают голоморфные функции перехода
|
z(ζ) = |
1 |
, |
ζ(z) = |
1 |
. |
|
|
ζ |
|
|||||
|
|
|
|
|
z |
||
Получаем поверхность |
|
с топологией сферы («сферу Римана»). |
|||||
|
|||||||
Топологическая эквивалентность со стандартной сферой дается стереографической проекцией, где одни из полюсов сферы переходит в точку ∞.
2. Другое описание – это комплексная проективная прямая
P1 ={(z1 : z2 ) : z1 + z2 ≠ 0 }, (z1 : z2 ) (λz1 : λz2 ) , λ , λ ≠ 0 .
1 |
≈ |
|
|
|
|||
Эквивалентность P |
→ устанавливается так |
||
25
|
(z : z |
) → z = |
z1 |
. |
|
|
|
|
|
||||||
|
1 |
2 |
|
z2 |
|||
|
|
|
|
||||
Аффинная часть |
P1 = {z |
≠ 0} – переходит в |
|
, а бесконечно- |
|||
|
|||||||
|
2 |
|
|
|
|
|
|
удаленная точка (1:0) – в ∞.
Чтобы компактифицировать любую (алгебраическую) риманову поверхность σ ={(z, w) : F(z, w) = 0} , вложим ее в P2 .
P2 – это (комплексная) проективная плоскость: совокупность ненулевых комплексных векторов (ξ: η: ζ) , определенных с точ-
ностью до умножения на ненулевой комплексный множитель
(ξ, η, ζ) (λξ: λη: λζ) , |
|
λ , |
λ ≠ 0 . |
|||||||
Это комплексное компактное многообразие. Область в P2 , задан- |
||||||||||
ная условием ζ ≠ 0 , называется аффинной частью |
P2 . |
|||||||||
Отображение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
, w = |
η |
|
|
|
(ξ: η: ζ) → z = |
ζ |
ζ |
|
|
||||||
и обратное |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
(z, w) →(z : w:1) |
|
|
|
|||||||
устанавливают изоморфизм аффинной части |
P2 и |
2 . Вся проек- |
||||||||
тивная плоскость получается из аффинной части |
2 добавлением |
|||||||||
бесконечно удаленной части вида |
|
|
|
|
|
|
|
|||
(ξ: η: 0) P1 S2 . |
|
|
|
|||||||
Вложение σ в P2 определяется следующим образом. |
||||||||||
Пусть |
|
|
|
|
|
|
|
|
|
|
ξ |
|
η |
Q(ξ, η, ζ) |
|
|
|
||||
F |
|
, |
= |
|
|
|
|
, |
|
|
ζ |
|
ζ |
N |
|
|
|||||
|
|
ζ |
|
|
|
|
|
|||
где Q(ξ, η, ζ) – однородный многочлен от ξ, η, ζ N-й степени. При
этом предполагается, что дробь, стоящая в правой части, несократимая.
26

Зададим в P2 комплексную кривую σˆ (двумерную поверхность) однородным уравнением
Q(ξ, η, ζ) = 0 .
Поверхность σˆ компактна и является поэтому искомой компактификацией поверхности σ.
Задача 7.2. Доказать, что кривая Q(ξ, η, ζ) = 0 неособа в P2 тогда и только тогда, когда
|
ξ |
η |
ζ |
|
|
∂Q |
∂Q |
|
= 2 . |
Rang |
∂Q |
|||
|
∂ξ |
∂η |
|
|
|
∂ζ |
|
8. ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
Пример 8.1. Пусть риманова поверхность задается уравнением
F(z, w) = 0 , где F(z, w) = w2 − z , т.е. σ: w2 = z . Точка |
P (0, 0) |
– |
|
0 |
|
точка ветвления поверхности σ. Локальным параметром в точке
ветвления |
P0 является τ= z , т.е. в некоторой окрестности |
U (P ) |
2 σ задается параметрически |
0 |
|
z =τ2 ; σ:
w = τ.
Компактификация римановой поверхности σ имеет вид
σˆ : η2 =ξζ.
Введем координаты u, v в окрестности несобственной прямой P1 (с ξ ≠ 0 ), полагая
u = ηξ = wz ;v = ζ = 1 ,ξ z
27

причем несобственная прямая имеет вид v = 0 . В этих координатах
кривая σˆ записывается (локально) в виде u2 = v . Ее единственная бесконечно удаленная точка – это (0, 0) . Локальным параметром в
окрестности этой точки служит |
u = w |
= v |
= |
|
1 |
. Другими слова- |
||||||
|
z |
|||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
ми, в окрестности бесконечно удаленной точки |
|
|
||||||||||
z = |
1 |
|
; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
u |
2 |
|
|
|
|
|
|
|
|
||
σ: |
|
|
u →0 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
||
w = |
|
|
|
|
, |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
Пример 8.2. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
σ: w2 = z2 −a2 . |
|
|
|
|
||||||||
Точки ветвления P1(−a, 0) и P2 (a, 0) , соответствующие локальные
параметры τ− = |
z −a и τ+ = |
z + a . Компактификация имеет вид |
|||||||||||
|
|
|
σˆ : η2 =ξ2 −a2ζ2 . |
|
|||||||||
Делая замену |
|
|
|
|
|
|
|
|
w |
|
|
||
|
|
|
|
|
|
η |
|
|
|
|
|||
|
|
|
u = |
|
= |
|
|
|
; |
|
|||
|
|
|
ξ |
|
z |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
v = ζ = |
, |
|
|
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
ξ |
|
|
z |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
получаем вид |
кривой |
σˆ в |
окрестности |
несобственной прямой: |
|||||||||
u2 =1 −a2v2 . |
При v = 0 |
получаем |
u = ±1 . |
Следовательно, на по- |
|||||||||
верхности σˆ |
есть две бесконечно удаленные точки P− (1, −1, 0) и |
||||||||||||
P+ (1,1, 0) . В качестве локального параметра в окрестности каждой |
|||||||||||||
из этих точек можно взять v |
= |
1 |
. Вид поверхности σˆ в окрестно- |
||||||||||
z |
|||||||||||||
сти точек P− , |
P+ таков: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
28
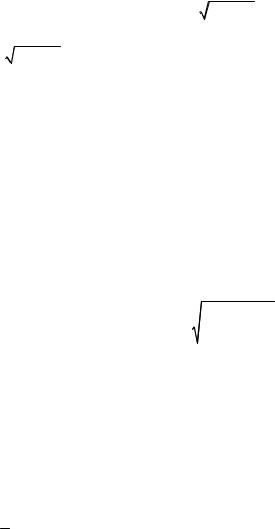
|
z = |
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σˆ : |
|
v |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
2 |
|
2 |
|
|
|
w = |
|
1 |
−a |
v |
|
, |
||
|
v |
|
|||||||
|
|
|
|
|
|
|
|
|
|
где 1−a2v2 – однозначная голоморфная при малых v функция, причем ветвь корня выбирается так, чтобы при v = 0 он обратился в единицу.
Пример 8.3. Пусть риманова поверхность
2n+1
σ: w2 = P2n+1 (z) =∏(z − zj ) .
j=1
Этот пример аналогичен примеру 8.1. В данном случае имеется одна бесконечно удаленная точка; в качестве локального параметра в
ее окрестности можно взять u. Поверхность σˆ в окрестности бесконечно удаленной точки имеет вид
|
|
1 |
|
|
|
||
|
z = |
|
|
|
; |
|
|
|
u |
2 |
|
||||
σˆ : |
|
|
|
|
|
||
|
|
|
|
1 |
2n+1 |
||
|
w = |
|
|
|
∏(1 − z ju), |
||
|
|
|
|
2n+1 |
|||
|
|
|
u |
|
|
j=1 |
|
|
|
|
|
|
|||
где корень является однозначной голоморфной функцией от u при малых u, обращающейся в единицу при u =0 .
Пример 8.4. Пусть
2n+2
σ: w2 = P2n+2 (z) = ∏(z − z j ) .
j =1
Этот пример аналогичен примеру 8.2. Здесь у σˆ две бесконечно удаленные точки P− , P+ , в окрестностях которых можно взять
v = 1z за локальный параметр. Вид компактифицируемой поверх-
ности σˆ в окрестности этих точек таков:
29
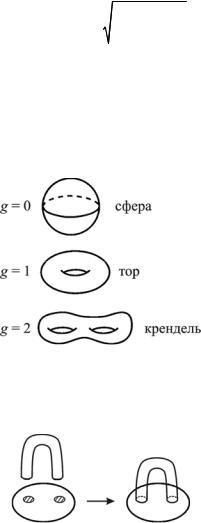
|
|
1 |
; |
|
|
|
z = |
v |
|
||
σˆ : |
|
|
|
|
|
|
|
|
1 |
2 n+2 |
|
|
w = ± |
∏(1− z jv); |
|||
|
n+1 |
||||
|
|
|
|
v |
j=1 |
|
|
|
|
||
корень является однозначной голоморфной функцией от v при малых v, обращающейся в единицу при v = 0 .
Хорошо известно, что связные компактные ориентированные двумерные поверхности поддаются простой топологической классификации (рис. 8.1). Все они есть сферы с g ручками, g ≥ 0 . Число
ручек g называется родом поверхности.
Рис. 8.1
Операция приклейки ручки изображена на рис. 8.2.
Рис. 8.2
30
