Добавил:

Yragan2404 Yragan в дс | @yragan2404 | ну, короче, вы поняли. Пишите сразу сообщение, отвечу по возможности. Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

Сопротивление материалов

Файл:

Лекции Алексеевой

.pdf

Скачиваний:

Добавлен:

08.11.2022

Размер:

13.28 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2717 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Для произвольного закрепления торцов стержня

	2	EJ
F		EJ	min
F			min
кр	( l)			2
	( l)
l
– приведенная (расчетная) длина стержня,
– коэффициент приведения длины,

n – число полуволн при потере устойчивости.

Коэффициент приведения длины показывает, во сколько раз следует увеличить длину стержня, чтобы его критическая сила равнялась критической силе шарнирно опертого стержня.

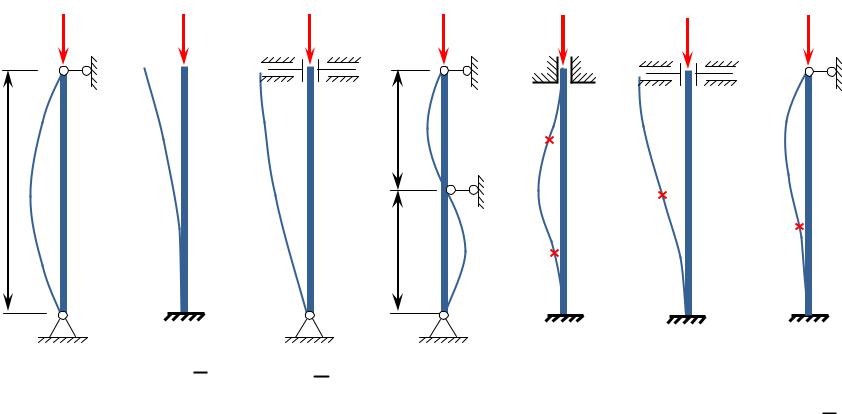
	Значения для основных условий закрепления
F	F	F	F	F	F	F
	F		F	F


			0,5l
l
			0,5l
n 1	n 1	n 1	n 2	n 2	n 1	0,7
	2	2				n 3
1	2	2	0,5	0,5	1	n 3
1	2	2	0,5	0,5	1	2
						2

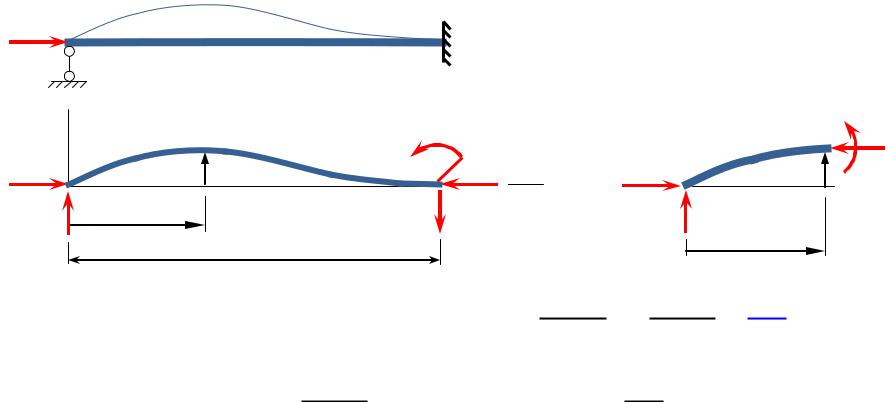
Пример. Найти F	,
кр

F			v
кр			v
кр
R	z
R				l
				l
	EJ			M
	EJ	min	v	M	x
		min			x

– ?

M Rl

		F
		кр	z
			z
		R
			F
F	v R z		кр
F	v R z	v
кр			EJ
			EJ
			min

	F
	кр
		R
	v	R
	v	EJ
		EJ
		min

кр

v k

z .

min

кр

M x v

	z
	F
z	кр	.
z	F	.
	F
	кр

Fкр

Решение ДУ:

v C1 sin kz

cos kz	R	z ,		C k cos kz C k sin kz		R

			v
	F			1	2	F
	F					F
	кр					кр
v* частное решение

Для определения трех неизвестных

1) при	z 0,	v 0;		C	0
1) при				1

C1 C2

C2 1

и R имеем три ГУ:

R	0	0	C		0.
F	0	0	C	2	0.
				2

кр

2)	при z l, v 0;		C1 sin kl	R			l 0.
2)	при z l, v 0;		C1 sin kl				l 0.
				Fкр					(*)
									(*)
						R

3)		0;	C1k cos kl					0.
3)	при z l, v	0;	C1k cos kl					0.
					Fкр

Система (*) имеет отличное от составленный из коэффициентов при

	sin kl		1
	sin kl		F
			F
			кр
F 0,		sin kl kl
кр
Это трансцендентное		уравнение,
Наименьший корень	kl 4, 49

нуля решение, когда определитель, неизвестных равен нулю

kl	cos kl 0		,
F


кр
cos kl 0				tgkl kl .
которое		решается только численно.

k 2

4, 492

Fкр

4,492 EJ

min

2EJ

min

2EJ

min

l 2

EJmin

0,7l 2

4,49

0,7 .

4, 49

Fкр

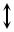
Энергетический метод

U – потенциальная энергия деформации

W F	– работа внешней постоянной силы.

Если U W , то после устранения причин, вызвавших отклонение, стержень вернется в исходное состояние, значит F Fкр .

Если U W , стержень не вернется в исходное
состояние, значит F F .
		кр
Если U W , имеем F F .
			кр
U W F	F		U	.

кр	кр

Потенциальная энергия деформации стержня при изгибе

sin 2 2

						M x
	2			l						2				1	l			2
M x						(EJminv )								1				2
		dz									dz					EJmin (v )			dz .
2EJ	min	dz				2EJ	min				dz			2		EJmin (v )			dz .
	min			0			min								0
		Перемещение											можно определить как разность
между				длиной					l		и		проекцией					изогнутой				упругой
линии на вертикаль. Для элемента длиной dz
		d dz dz cos dz(1 cos ) dz 2sin																			2		,
																					2
																						2
																						2
d			1			2		1		2							1 l0		2	dz ,
d			2		dz			2	(v )			dz					2	(v )		dz ,
			2					2									2	0
																		0

интегрирование ведется по длине l0 участка стержня, сжимаемого силой F.

	l
				2	dz
	EJmin (v )				dz
F	0
кр	l
	0
		2	dz
	(v )		dz
	0

(1)

– геометрическая длина стержня;

l0 – длина участка стержня, сжимаемого силой.

Определение точного значения

Fкр

по (1) возможно

только в том случае, если известна точная функция прогибов v(z) .

Например, для шарнирно-опертого стержня

																																								2
			v C sin				z ,														C					cos					z ,	v		C							sin			z ,

																			v
				1		l																1		l					l								1	l	2				l
																																							2


							2					4	l				2															1		l							2
						C	2							sin			2			z dz												1				1	cos				2		z	dz
						C				4				sin						z dz							2									1	cos						z	dz
						1			l	4									l								2	EJ				2									l
		F	EJ						l				0						l									EJ		min		2		0							l
		F	EJ		min						2		0																2	min				0
		кр			min		2				2		l					2										l	2			1	l								2
							2							cos				2			z dz							l				1			1 cos						2	z		dz
						1				2
						C			l										l													2									l
									l				0						l													2	0								l
													0																				0
						l							2						l																			0
																																						0
																																l
2				dz					sin							z							2								l	l		sin 2 sin 0											2
2	EJmin			dz		2			sin				l			z							2	EJmin							l	2		sin 2 sin 0											2	EJmin
	EJmin					2							l						0					EJmin								2														EJmin
	l	2																	l					l	2							l														l	2
		2				l							2						l						2						l	l		sin 2 sin 0													2


				dz		2		sin					l		z																	2
						2							l						0																			0
																																						0

Значение Fкр совпадает с формулой Эйлера (точным решением), поскольку

в качестве функции прогибов v(z) взято ее точное выражение.

В большинстве случаев функция прогибов неизвестна. Задаваясь приблизительным выражением функции прогибов v(z) , удовлетворяющим ГУ, можно определить приближенное значение Fкр . Чем ближе эта функция будет подобрана к

точному выражению прогибов, тем точнее будет значение

Fкр

В качестве функции

v(z)

берут такую, которая удовлетворяет

обязательно!! кинематическим ГУ (v, v ) , и желательно! статическим ГУ (v , v ) .

Самый лучший вариант – полином степени n, где n – число ГУ!

v(z) a a z a z2		a z3		a zn .
0 1	2	3		n

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2717 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
08.11.202213.28 Mб30Лекции Алексеевой.pdf
#
08.11.202216.16 Mб16Семинары Алексеевой.pdf
#
08.11.202226.78 Кб4Универсальный шаблон с основной надписью.docx