Геометрические понятия. Дифференцирование единичного вектора

Радиус кривизны и соприкасающаяся плоскость. В точке кривой линии проведем касательную : (рис. 12). В другой близкой точке кривой , отстоящей от точки на расстоянии , построим касательную . В общем случае пространственной кривой касательные и будут с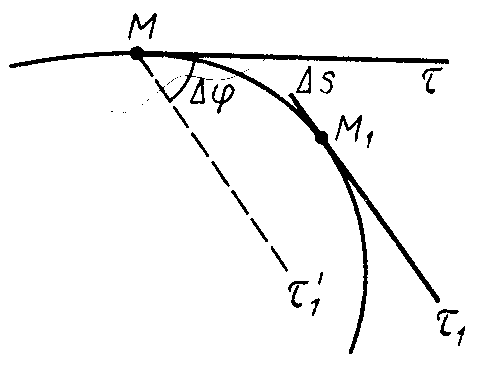 крещиваться. Проведем в точке прямую линию , параллельную . Угол между линиями и называется углом смежности. Кривизной кривой в точке называют предел, к которому стремится угол смежности, п

Рис. 12

риходящийся на единицу расстояния , причем стремится к нулю, т.е.

.

Радиусом кривизны кривой в точке называют величину, обратную кривизне кривой в этой точке, т. е.

.

В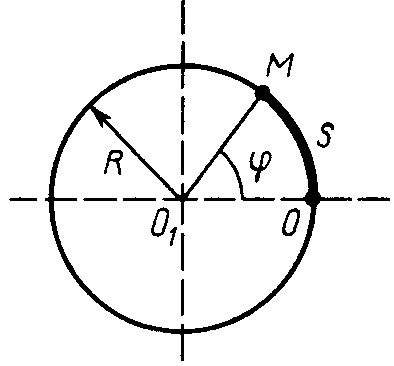 ычислим радиус кривизны дуги окружности радиусом . (рис. 13). Дуга окружности длиной , опирающаяся на центральный угол , выражается зависимостью . Для радиуса кривизны имеем:

,

т

Рис. 13

.е. для окружности радиус кривизны в каждой ее точке один и тот же и совпадает с радиусом окружности.

Участок кривой из малой окрестности какой-либо ее точки лучше всего аппроксимирует по сравнению с дугами других окружностей элемент дуги окружности, радиус которой равен радиусу кривизны кривой в рассматриваемой точке.

Для определения понятия соприкасающейся плоскости проводим вспомогательную плоскость через две пересекающиеся прямые и (см. рис. 12). Предельное положение этой плоскости при совпадении в пределе точки с точкой называется соприкасающейся плоскостью кривой в точке .

В случае плоской кривой соприкасающейся плоскостью для всех точек кривой является сама плоскость, в которой расположена эта кривая.

Е

Рис. 14

стественный трехгранник. Построим в точке кривой линии естественные оси этой кривой (рис. 14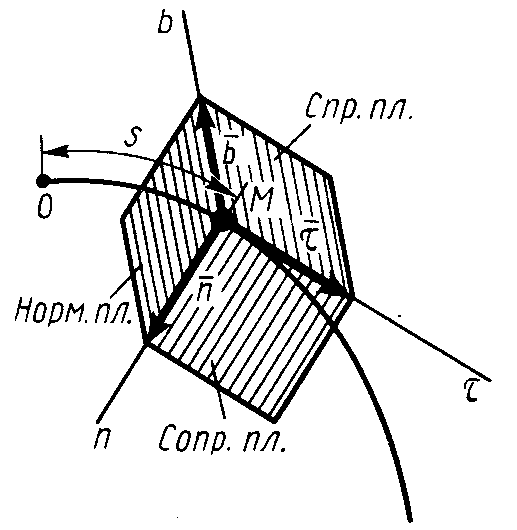). Первой естественной осью является касательная . Ее положительное направление совпадает с направлением единичного вектора касательной , направленного в сторону возрастающих расстояний.

Перпендикулярно касательной располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью . Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь вогнутости кривой направим единичный вектор . Он определяет положительное направление второй естественной оси.

Нормаль, перпендикулярная главной нормали, называется бинормалью. Единичный вектор , направленный по бинормали так, чтобы три вектора , и образовывали правую систему осей координат, определит положительное направление третьей естественной оси.

Три взаимно перпендикулярные оси , и , положительные направления которых совпадают с направлениями единичных векторов , и , называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.

Дифференцирование единичного вектора. Вычислим производную от единичного вектора по скалярному аргументу. В кинематике точки скалярными аргументами обычно являются время и расстояние по траектории. В качестве единичного вектора выберем , направленный по касательной к траектории, и вычислим его производную по времени.

Производная перпендикулярна самому единичному вектору . Для доказательства этого используем тождество:

.

Дифференцируя по времени обе части этого тождества, получим

.

Каждый из сомножителей этого выражения не равен нулю, поэтому векторы и перпендикулярны друг другу. Это справедливо для любого другого вектора, числовая величина (модуль) которого постоянна. Направим по вектору единичный вектор . Тогда

. (15)

Годографом вектора является кривая, расположенная на сфере единичного радиуса, так как единичный вектор изменяется только по направлению (рис. 15).

По определению модуля производной от вектора имеем

.

Д лина малой хорды с точностью до малых величин более высокого порядка равна длине дуги, которую стягивает хорда, т. е.

,

г

Рис. 15

де – угол, опирающийся на эту дугу. Используя это выражение, получим

.

Подставляя это значение в (15) и используя выражение для радиуса кривизны и переменную , получим

.

Радиус кривизны считаем положительным.

Вектор и совпадающий с ним по направлению единичный вектор направлены параллельно предельному положению вектора при , стремящемся к нулю, т.е. они расположены в соприкасающейся плоскости кривой. Единичный вектор перпендикулярен вектору , направленному по касательной к кривой. Следовательно, вектор направлен по главной нормали кривой в сторону ее вогнутости, так как в эту сторону направлено предельное положение вектора .

Если имеем любой другой вектор с постоянным модулем, то для него остается справедливым все, что было получено для единичного вектора, только радиус годографа следует заменить его модулем . Получим

, (16)

где – теперь единичный вектор, перпендикулярный вектору и направленный параллельно .

Формулу (16) можно выразить векторным произведением:

,

где – вектор угловой скорости поворота вектора , модуль которого . Вектор угловой скорости следует направить перпендикулярно плоскости, в которой расположены векторы и , причем так, чтобы с его стрелки увидеть поворот вектора к в этой плоскости на угол 90° против часовой стрелки. Подробнее понятие вектора угловой скорости дается при рассмотрении вращения твердого тела вокруг неподвижной оси и в других случаях его движений.