6.3. Сложение поступательного и вращательного движений твердого тела

Если тело одновременно участвует в переносном поступательном движении со скоростью и относительном вращательном с угловой скоростью , то в зависимости от их взаимного расположения целесообразно рассмотреть три отдельных случая.

Скорость поступательного движения перпендикулярна оси относительного вращения

В этом случае векторы и перпендикулярны (рис. 79). На линии , перпендикулярной плоскости, в которой расположены и , имеется точка , скорость которой равна нулю. Определим ее расстояние от точки .

П

Рис. 79

о теореме сложения скоростей для точки имеем

,

так как при вращении вокруг оси .

Учитывая, что скорости и противоположны по направлению, получим

.

Так как , то и, следовательно, точки и находятся на расстоянии

. (146)

Другие точки, имеющие скорости, равные нулю, располагаются на линии, проходящей через точку , параллельно оси вращения тела с угловой скоростью . Таким образом, имеется мгновенная ось вращения, параллельная оси относительного вращения и проходящая через точку . Для определения угловой скорости абсолютного вращения вычислим скорость, например, точки двумя способами. Считая движение сложным, имеем

.

Точка находится на оси относительного вращения, и поэтому . Скорость переносного движения в рассматриваемом случае переносного поступательного движения равна . Следовательно, , . С другой стороны, эквивалентное абсолютное движение тела является вращением вокруг мгновенной оси, проходящей через точку с угловой скоростью . Поэтому для скорости точки имеем

.

Приравнивая скорости точки , вычисленные двумя способами и используя (146), получаем

, или , или .

Вращение вокруг мгновенной оси должно иметь такое направление, чтобы скорость точки имела такое же направление, что и скорость . Отсюда получаем совпадение направлений вращения относительного и абсолютного вращений. Следовательно, . Таким образом, при сложении поступательного переносного и вращательного относительного движений твердого тела, у которого скорость поступательного движения перпендикулярна оси относительного вращения, эквивалентное абсолютное движение является вращением вокруг мгновенной оси, параллельной оси относительного вращения с угловой скоростью, совпадающей с угловой скоростью относительного вращения.

Такой же результат можно получить, если поступательное движение со скоростью заменить парой вращений , выбрав . Два вращения с угловыми скоростями и можно отбросить, так как , и абсолютным движением окажется вращение с угловой скоростью . Скорость поступательного движения равна моменту пары вращений. Приравнивая их, получим или

,

что совпадает с (146).

Еще одна интерпретация рассмотренного случая получается, если рассмотреть параллельный перенос скользящего вектора угловой скорости в точку . Такой перенос, как известно, следует компенсировать парой вращений, эквивалентной поступательному движению со скоростью .

На поступательное переносное и вращательное относительное с осью вращения, перпендикулярной к скорости переносного движения, разлагается плоское движение твердого тела. Так, плоское движение без скольжения колеса по прямой (рис. 80) можно составить из поступательного движения колеса в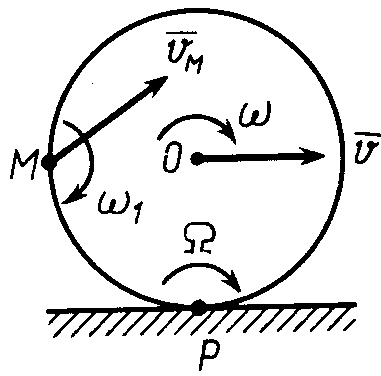 месте с центром со скоростью и относительного вращательного вокруг оси, проходящей через точку с угловой скоростью . Это же движение можно рассматривать как вращение вокруг мгновенной оси, проходящей через МЦС, который, совпадает с точкой . Угловая скорость этого абсолютного вращения , и оно имеет то же направление вращения, что и относительное вокруг оси, проходящей через точку . Если в качестве точки используется другая точка колеса, например точка , то изменится только скорость переносного поступательного движения. Она будет равна скорости точки . Угловая скорость вращения тела вокруг оси, проходящей через точку , по величине и направлению будет той же самой, что и вокруг осей, проходящих через точки и .