5.2. Сложение скоростей
Е
Рис. 65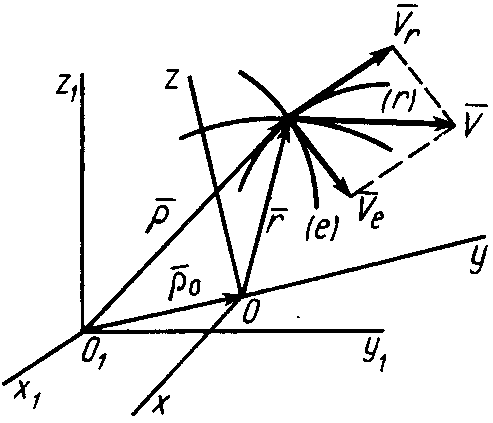
Движение
подвижной системы осей координат
относительно неподвижной можно
охарактеризовать скоростью ее
поступательного движения
,
например вместе с точкой
и вектором угловой скорости
ее вращения вокруг
.
Пусть точка
движется относительно подвижной системы
координат. Получим теорему сложения
скоростей. Для этого проведем векторы
и
,
характеризующие положение точки
относительно неподвижной и подвижной
систем осей координат, и вектор
точки
.
Для любого момента времени
. (127)
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
.
По
определению,
является абсолютной скоростью точки
,
– абсолютной скоростью точки
.
Для вычисления
применим формулу Бура. Имеем
.
Относительная
производная
является относительной скоростью точки
по отношению к подвижной системе отсчета,
а
– угловая скорость вращения подвижной
системы отсчета и, следовательно,
радиуса-вектора
,
если бы он в рассматриваемый момент
времени был скреплен с подвижной системой
осей координат. Таким образом, из (127)
получаем
. (128)
Скорость
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки . Из (128) получаем следующую теорему сложения скоростей для точки:
. (129)
т.е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
5.3. Сложение ускорений точки в общем случае переносного движения
Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости (128). Имеем
.
Для полных производных от векторов и , применим формулу Бура. Получим
,
.
Учитывая, что
,
,
,
,
получим для абсолютного ускорения
. (130)
В
этой формуле первые три слагаемых
составляют ускорение точки свободного
твердого тела в общем случае его движения
вместе с подвижной системой осей
координат относительно неподвижной.
Первое слагаемое
– ускорение точки
,
и
– соответственно вращательное и
осестремительное ускорения точки
,
если бы она двигалась только вместе с
подвижной системой осей координат, не
имея в рассматриваемый момент времени
относительного движения. После этого
(130) примет вид
, (131)
где
. (132)
Ускорение
называется ускорением
Кориолиса.
Иногда его также называют добавочным
(или поворотным)
ускорением.
Формула (131) выражает теорему сложения ускорений точки, или кинематическую теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений – переносного, относительного и Кориолиса.
Переносное ускорение рассматривалось при изучении движения свободного твердого тела. Относительное ускорение изучалось в кинематике точки. Его можно выразить в двух формах в зависимости от способа задания относительного движения. При координатном способе задания в декартовых координатах
,
где – координаты движущейся точки относительно подвижной системы осей координат; – единичные векторы этих осей. При естественном способе задания движения
,
,
,
где
– расстояние от начала отсчета до точки
по траектории относительного движения;
– радиус кривизны этой траектории. В
частном случае, когда переносное движение
есть вращение вокруг неподвижной оси,
переносное ускорение
,
где касательное переносное ускорение
,
причем – кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
.
Абсолютное ускорение в этом случае
. (133)