Уравнения движения свободного твердого тела

В общем случае для определения положения свободного твердого тела относительно системы координат достаточно задать относительно этой системы координат положение другой системы координат , движущейся поступательно относительно первой системы вместе с какой-либо точкой рассматриваемого тела, и углы Эйлера, определяющие положение системы координат , скрепленной с движущимся телом, относительно системы координат (рис. 60).

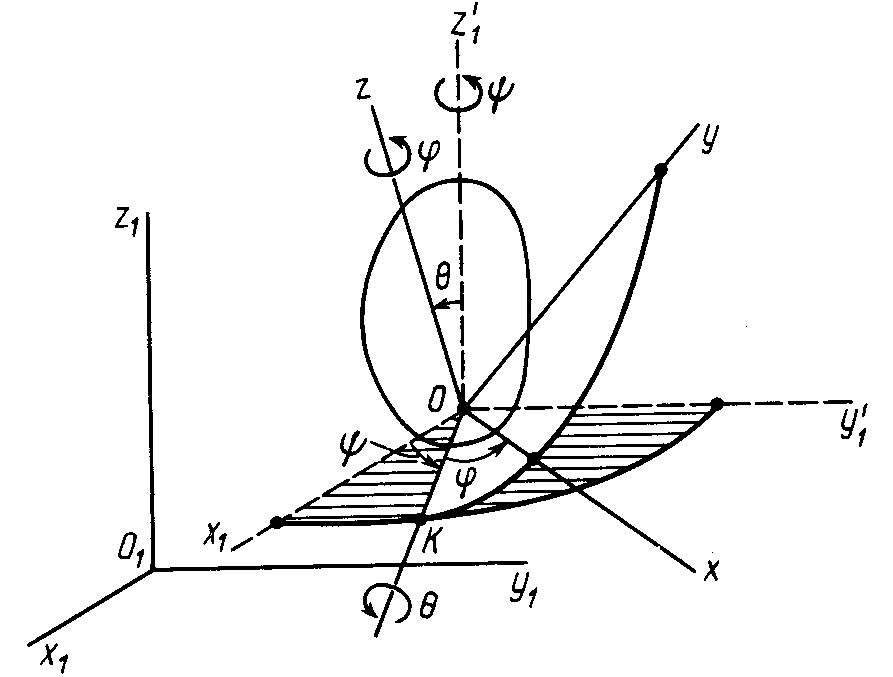
Рис. 60

Для простоты предположим, что оси , , соответственно параллельны осям , , . Таким образом, положение свободного твердого тела относительно системы координат полностью определяется, если относительно этой системы задать координаты точки тела как однозначные функции времени и углы Эйлера подвижной системы координат , скрепленной с движущимся телом, относительно системы координат , поступательно движущейся вместе с точкой тела:

, , ,

, , . (115)

Уравнения (115) являются кинематическими уравнениями движения свободного твердого тела в общем случае его движения. Этих уравнений шесть, т.е. столько, сколько степеней свободы у свободного твердого тела. Первые три уравнения (115) определяют переносное движение тела вместе с точкой , вторые три уравнения определяют вращательное движение вокруг этой точки.

Первые три уравнения для рассматриваемого движения свободного твердого тела зависят от выбора точки тела; последние три уравнения (углы Эйлера) не зависят от выбора точки , вокруг которой рассматривается вращение тела.

Скорости и ускорения точек свободного твердого тела в общем случае

Так как движение свободного твердого тела в общем случае можно представить как сложное движение, то и скорость, и ускорение какой-либо точки этого тела можно вычислить соответственно по теоремам сложения скоростей и ускорений (рис. 61). Так, для скорости точки

_.

Переносным движением является поступательное движение тела вместе с точкой этого тела. Следовательно, скорости поступательного переносного движения одинаковы у всех точек тела и равны скорости точки . Относительное движение есть вращение вокруг точки , и, следовательно, скорость относительного движения м

Рис. 61

ожно вычислить по векторной формуле Эйлера:

,

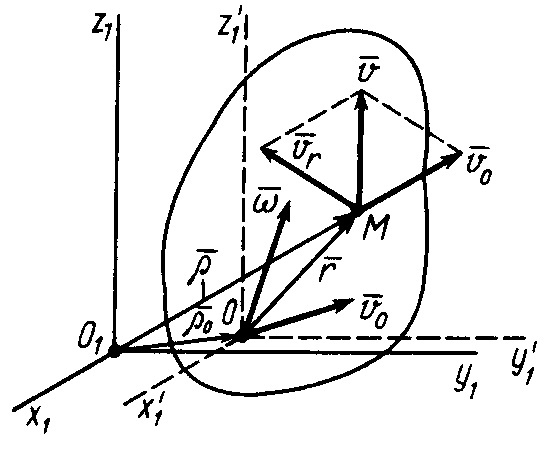где – радиус-вектор точки , проведенный из точки ; – угловая скорость вращения тела вокруг точки или подвижной мгновенной оси, проходящей через точку .

Окончательно для скорости точки получим следующую формулу:

. (116)

Формулу (116) можно получить непосредственным дифференцированием векторного равенства

,

справедливого для любого момента времени. Возьмем полные производные по времени от обеих частей равенства, учитывая изменения векторов относительно неподвижной системы координат . Имеем

.

Здесь , – скорости точек тела и соответственно. Модуль вектора как отрезка, соединяющего две точки тела, не изменяется при движении этого тела. Следовательно, по формуле производной по времени от вектора постоянного модуля получаем

.

Объединяя результаты, получаем формулу (116):

.

Так же как и при плоском движении твердого тела, часть скорости можно истолковать как скорость от вращения тела вокруг точки .

У

Рис. 62

скорение точки (рис. 62) в частном случае, когда переносное движение является поступательным, определяем по формуле

.

Ускорения переносного движения всех точек тела равны ускорению точки , так как за поступательное переносное движение принимается движение вместе с точкой .

Ускорение относительного движения, как и при вращении тела вокруг неподвижной точки, состоит из вращательной и осестремительной составляющих, т.е.

, (117)

где – угловое ускорение тела.

Окончательная формула для ускорения точки свободного тела в общем случае его движения имеет вид

, (118)

на основании формулы Ривальса

, (119)

где

, .

Формулу (118) можно получить непосредственным дифференцированием векторного равенства для скоростей (116), справедливого в любой момент времени. Вычисляя полные производные по времени, при определении которых учитываются изменения векторов относительно неподвижной системы координат, получаем

.

Здесь , – ускорения точек и ; – угловое ускорение.

Учитывая, что вектор является вектором постоянного модуля, имеем

.

Окончательный результат выразится в форме

.

Заметим, что если в кинематике свободного твердого тела в качестве точки можно брать любую точку тела, то в динамике в качестве такой точки оказывается выгодным выбирать центр масс тела.

П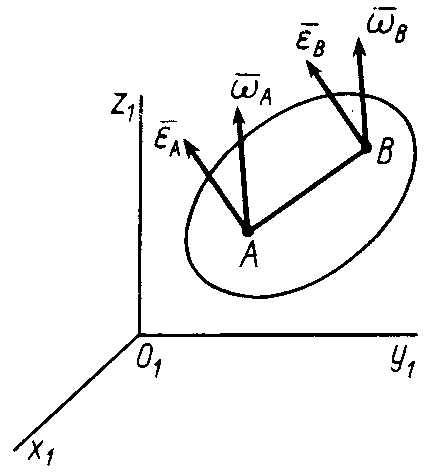 ри выборе различных точек тела в качестве полюса изменяются скорость и ускорение полюса. Угловая скорость и угловое ускорение при этом не изменяются. Докажем это для угловой скорости, используя (116).

Пусть и – две точки свободного твердого тела (рис. 63). Приняв за полюс точку , для скорости точки имеем

Рис. 63

, (120)

где – угловая скорость вращения тела вокруг точки . Аналогично, приняв за полюс точку , для скорости точки получим

, (121)

где – угловая скорость вращения тела вокруг точки . Из (120) и (121) имеем

,

для любых двух точек свободного твердого тела. Эти точки можно выбрать так, чтобы не было параллельно вектору . Тогда получаем

, , (122)

т.е. угловая скорость свободного твердого тела не зависит от выбора полюса. Она инвариантна по отношению к выбору полюса. Так как равенство (122) справедливо для любого момента времени, то, дифференцируя его по времени, получим

, ,

т.е. вектор углового ускорения свободного твердого тела тоже не зависит от выбора полюса.