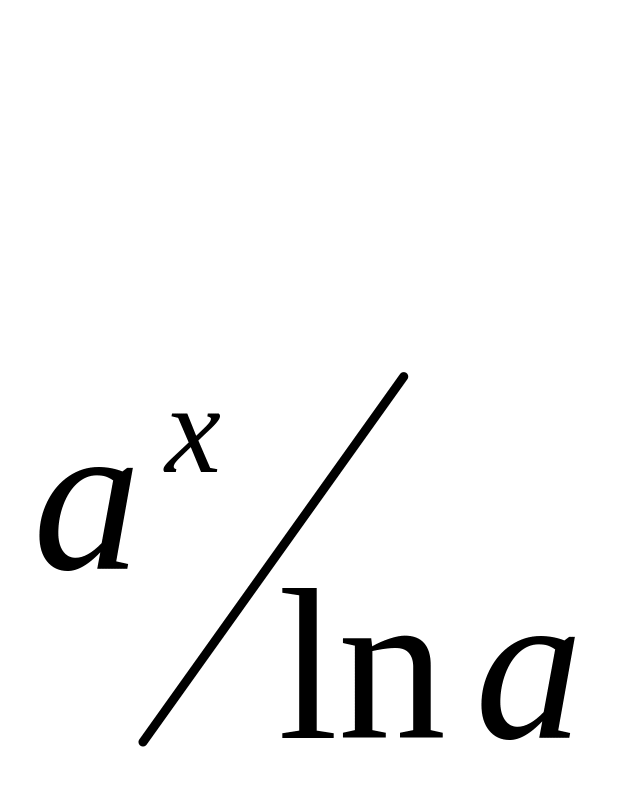- •Часть 1
- •Введение
- •Методические указания
- •Контрольная работа по физике №1
- •Студента группы рк-001
- •Шифр 257320
- •Иванова Петра Ивановича
- •1. Механика
- •Кинематика материальной точки и поступательного движения абсолютно твёрдого тела
- •1.2. Динамика материальной точки и поступательного движения абсолютно твердого тела
- •1.3.Кинематика вращательного движения абсолютно твёрдого тела
- •1.4. Динамика вращательного движения
- •1.4.1. Момент инерции и момент импульса
- •1.4.2. Момент силы. Основной закон динамики вращательного движения
- •1.5.Механическая энергия, работа и мощность
- •1.5.1 Механическая работа при поступательном движении
- •1.5.2. Кинетическая и потенциальная энергия
- •1.5.3. Работа и мощность при вращательном движении
- •1.6. Законы сохранения
- •1.6.1. Закон сохранения импульса
- •1.6.2. Закон сохранения момента импульса
- •1.6.3. Закон сохранения механической энергии
- •1.7. Механика жидкостей и газов
- •1.7.1. Идеальная жидкость. Уравнение неразрывности. Уравнение Бернулли
- •1.7.2. Вязкость. Ламинарный и турбулентный режимы течения жидкостей
- •1.8. Механика деформируемых тел
- •1.8.1. Идеально упругое тело. Упругие напряжения
- •1.8.2 Одноосное растяжение и сжатие
- •1.8.3. Сдвиг
- •1.8.4. Кручение
- •1.9. Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задача № 6
- •Решение.
- •Решение
- •Решение
- •Решение
- •1.10. Задачи для контрольных заданий
- •2. Основы молекулярно - кинетической теории
- •2.1. Идеальный газ. Уравнение состояния. Основное уравнение молекулярно - кинетической теории
- •2.2. Распределение молекул по скоростям
- •2.3. Идеальный газ в поле сил тяжести. Распределение Больцмана
- •2.4. Эффективный диаметр и средняя длина свободного пробега молекул
- •2.5. Внутренняя энергия идеального газа. Теплота и работа. Первое начало термодинамики
- •2.6. Изопроцессы. Применение первого начала термодинамики к различным процессам. Адиабатный процесс
- •2.7. Круговые процессы. Цикл Карно. Второе начало
- •2.8. Энтропия
- •2.9. Примеры решения задач
- •Решение
- •Решение.
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Р ешение
- •Решение
- •2.10 Задачи для контрольных заданий
- •2.16. Азот находится при нормальных условиях. Найти:
- •3. Электростатика
- •3.1. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона
- •Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции полей
- •3.3. Линии напряжённости. Поток вектора напряжённости. Теорема Гаусса
- •3.4. Работа сил электрического поля. Потенциал
- •3.5. Эквипотенциальные поверхности. Связь между напряженностью и потенциалом
- •3.6. Проводники в электрическом поле
- •3.7. Диэлектрики в электрическом поле
- •3.8. Электроемкость уединенного проводника.
- •3.9. Энергия электрического поля
- •3.10. Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •3.11. Задачи для контрольных заданий
- •4. Законы постоянного тока
- •4.1. Сила и плотность тока. Сторонние силы, эдс и напряжение
- •4.2 Обобщённый закон Ома. Дифференциальная форма закона Ома
- •4.3. Работа тока. Закон Джоуля - Ленца
- •4.4. Правила Кирхгофа и их применение к расчёту электрических цепей
- •4.5. Примеры решения задач.
- •Решение
- •Подставляя это выражение в (1), получим
- •Решение Из условия равномерности возрастания тока следует
- •Решение
- •4.6. Задачи для контрольных заданий
- •5. Варианты контрольных заданий
- •П. 1. Скалярное произведение двух векторов
- •П. 1. Векторное произведение двух векторов
- •Приложение 2
- •П. 2. Таблица простейших производных.
- •Приложение 3 Элементы интегрального исчисления Интегрирование– действие обратное дифференцированию
- •Неопределенный интеграл
- •Приложение 4
- •Приложение 5 Некоторые астрономические величины
- •Приложение 6 Основные физические постоянные
- •Приложение 7 Плотности ρ твёрдых тел, жидкостей и газов
- •Приложение 8 Диэлектрическая проницаемость ε
- •Удельное сопротивление ρ и температурный коэффициент α проводимости
- •Заключение
- •Библиографический список
- •Оглавление Введение…………………………………………………………..3
- •Кинематика материальной точки и поступательного движения абсолютно твёрдого тела……………….….5
- •1.2. Динамика материальной точки и поступательного
- •2.5. Внутренняя энергия идеального газа. Теплота и работа.
- •Часть 1 механика, молекулярная физика, термодинамика и электродинамика
- •394026 Воронеж, Московский просп.,14
- •Часть 1
П. 1. Скалярное произведение двух векторов
![]() ,
,
где угол между векторами и .
В декартовой системе координат
![]()
П. 1. Векторное произведение двух векторов
![]() ,
,
![]() ,
,
где
- угол
между векторами
и
![]() ..
..

 Вектор
перпендикулярен
плоскости в которой располо- жены векторы
и
причем, три вектора (
,
,
)
Вектор
перпендикулярен
плоскости в которой располо- жены векторы
и
причем, три вектора (
,
,
)
образуют правую тройку векторов ( правило правого винта).
Приложение 2
П. 2. Производная от функции y = x)
![]()
Геометрический смысл производной – она численно равна тангенсу угла наклона касательной к кривой y = x в точке x. Если x , то при увеличении x
функция x возрастает, если x , то при возрастании x функция x уменьшается.
Функция |
С |
x |
x n |
ex |
a x |
lnx |
sinx |
cos x |
tg x |
ctg x |
Производнаяя |
0 |
1 |
nx n-1 |
ex |
ax lna |
1/x |
cosx |
-sin x |
|
|
П. 2. Таблица простейших производных.
П. 2. Дифференциал функции y = x
dy = y(x) dx.
Полный дифференциал функции нескольких переменных U = x y z
![]() ,
,
где
![]()
частные производные.
частные производные.
П. 2. Правила вычисления дифференциалов
1) d(C u) = C du ( C- const ),
2) d( u v) = du dv ,
3) d (u v) = u dv +v du ,
4) d (u /v) = (v du – u dv) / v2 .
Приложение 3 Элементы интегрального исчисления Интегрирование– действие обратное дифференцированию
dx = x.
Неопределенный интеграл
x dx = Fx + C ,
где Fx первообразная функция ( F x = x ) , C некоторая постоянная.
Определенным интегралом от функции y = x называется сумма бесконечно большого числа бесконечно малых слагаемых.
b n
x dx = Lim x i x I .
a x 0 i = 1
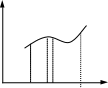
Геометрический смысл определенного интеграла это число, равное площади под кривой y = x, ограниченной ординатами: a нижний, b верхний пределы.
y
y=f(x)

a
b X
Таблица интегралов
Интеграл |
|
|
|
|
|
|
|
|
|
Первообразные |
|
|
|
|
|
|
|
|